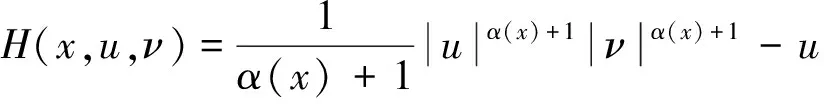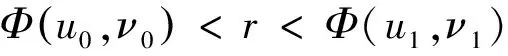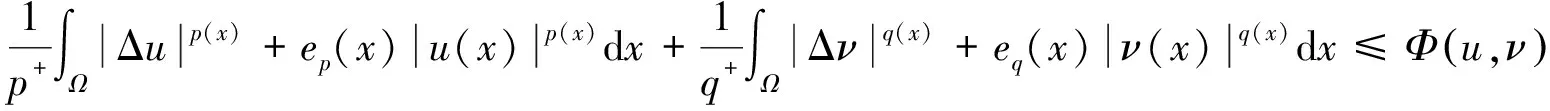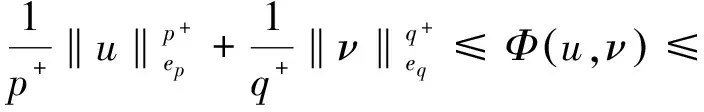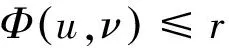带Navier边值条件的(p(x),q(x))-双调和问题的多解性
2015-06-24缪清
缪 清
(云南民族大学 数学与计算机科学学院,云南 昆明 650500)
带Navier边值条件的(p(x),q(x))-双调和问题的多解性
缪 清
(云南民族大学 数学与计算机科学学院,云南 昆明 650500)
研究了一类带Navier 边值条件的(p(x),q(x))双调和问题的存在性和多解性,利用Ricceri’s三临界点定理,得到问题至少存在3个弱解.
双调和; Ricceri’s临界点定理; 广义Lebesgue-Sobolev空间

(1)

(2)
(3)
函数G(x,t,s),ep(x),eq(x)满足以下条件:
(G):G:Ω×R×R→R为Ω上的可测函数,在R×R上是C1连续的且满足
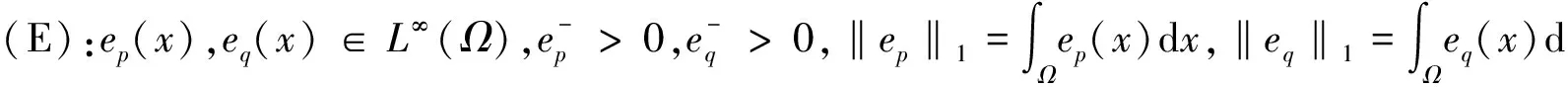
近年来,双调和问题的解的存在性和多解性引起了许多学者的兴趣[1-4]. 由于p(x)-双调和算子是非齐次的,因此很多适用于p-双调和算子的方法则不能直接应用于p(x)-双调和算子.文献[1]中,作者利用Ricceri’s三临界点定理,推广了文献[3]的结果,研究了p(x)-双调和问题多解的存在性.文献[2]中,作者利用了等价的Ricceri’s三临界点定理,推广了文献[4]的结果,研究了不同条件下带Navier边值条件的(p(x),q(x))-双调和问题的多解性. 本文主要利用Ricceri’s三临界点定理研究问题(1)的多解性. 首先给出Ricceri’s三临界点定理.
定理1[5]令X是自反的Banach空间,Φ:X→R是连续的Gateaux 微分算子且序列弱下半连续的C1函数, 在X的任意有界子集上,存在着连续的逆算子.Ψ:X→R是C1连续的且具有紧的Gateaux 微分算子. 假设
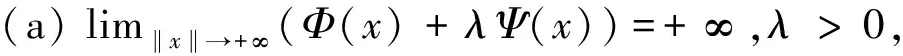
(b)Φ(u0) 则存在开区间Λ⊆[0,+∞),ρ为正实数,C1连续函数J:X→R是紧的Gateaux 微分算子,使得∀λ∈Λ,存在δ>0,∀μ∈[0,δ], 在X中问题Φ′(x)+λΨ′(x)+μJ′(x)=0至少存在3个解并且范数不超过ρ. 为了讨论问题 (1), 需要用到关于空间Lp(x)(Ω),Wm,p(x)(Ω)的一些性质. 记 当空间Lp(x)(Ω)空间赋如下范数时, 由文献[6]可知Lp(x)(Ω),Wm,p(x)(Ω) 是可分的自反的Banach 空间. 赋予范数 由文献[6]定理1.3,有不等式成立: (4) (5) (6) (7) 引理1[2]令Φ:X→X*为 其中u,ν,φ,ψ∈X. 证明 令 则Ψ,J都是Gateaux可微的并且满足 则Ψ′为紧算子. 接下来依次验证满足定理1的3个条件. 令 因为α(x)>0,则有lim|(u,ν)|→∞H(x,u,ν)=+∞.选取δ>1,∀u,ν>δ使得H(x,u,ν)>0,因而 H(x,u,ν)≥0=H(x,0,0)≥H(x,t1,s1),∀u,ν>δ,t1,s1∈(0,1). 因而可得 (8) 由(4)式和(5)式可知 结合(8)式可得 即定理1的条件(c)成立. 由γ1,γ2满足定理1条件(b),函数J(u,ν)满足定理1的条件,由定理1可知,问题(1)至少存在3个弱解,定理2得证. [1] YIN H, YANG Z.Three solutions for a Navier Boundary value system involving the(p(x);q(x))-Biharmonic operator [J]. British Journal of Mathematics and Computer Science, 2013, 3(3):281-290. [2] YIN H, XU M. Existence of three solutions for a Navier boundary value problem involving thep(x)-biharmonic operator[C]//Annales Polonici Mathematici. Sniadeckich 8, Po Box 21, 00-956 Warsaw 10, Poland:Polish Acad Sciences Inst Mathematics, 2013, 109(1):47-58. [3] LI C, TANG C L. Three solutions for a Navier boundary value problem involving the p-biharmonic[J]. Nonlinear Analysis:Theory, Methods & Applications, 2010, 72(3):1339-1347. [4] LI L, TANG C L. Existence of three solutions for (p, q)-biharmonic systems[J]. Nonlinear Analysis:Theory, Methods & Applications, 2010, 73(3):796-805. [5] RICCERI B.A three critical points theorem revisited[J].Nonlinear Anal,2009,70:3084-3089. [6] FAN X, ZHAO D.On the spaces and [J] . Journal of Mathematical Analysis and Applications, 2001, 263(2):424-446. [7] ZANG A, FU Y. Interpolation inequalities for derivatives in variable exponent Lebesgue-Sobolev spaces[J]. Nonlinear Analysis:Theory, Methods & Applications, 2008, 69(10):3629-3636. (责任编辑 梁志茂) Multiplicity results of(p(x),q(x))biharmonicoperator with Navier boundary conditions MIAO Qing (School of Mathematics and Computer Science,Yunnan Minzu University,Kunming 650500,China) This paper proves the existence of at least three solutions to a Navier boundary problem involving the(p(x),q(x))biharmonic operator.The main results are new.The technical approach is mainly based on a three critical points theorem of B.Ricceri. (p(x),q(x))biharmonic;Ricceri′s critical points theorem;generalized Lebesgue-Sobolev spaces 2014-10-01. 国家自然科学基金(11461083,11361076);云南省自然科学基金(2013FD031). 缪清(1984-),女,博士,讲师. 主要研究方向:偏微分方程及应用. O175.6 A 1672-8513(2015)04-0285-05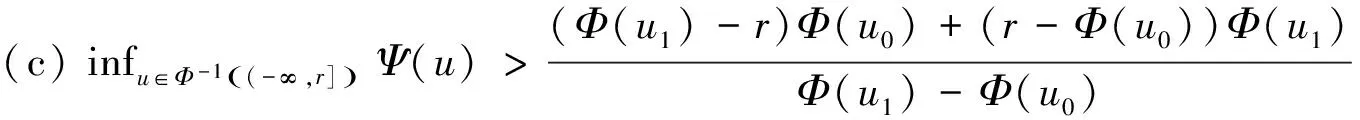
1 p(x)-双调和算子在空间 Lp(x)(Ω),Wm,p(x)(Ω)中的重要性质

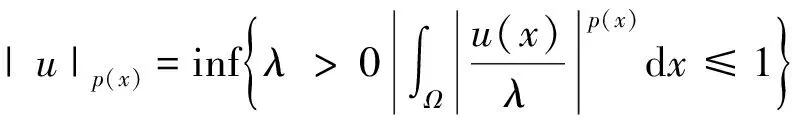


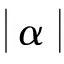



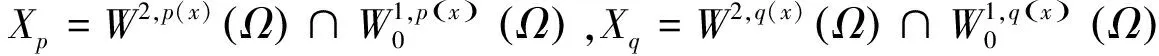
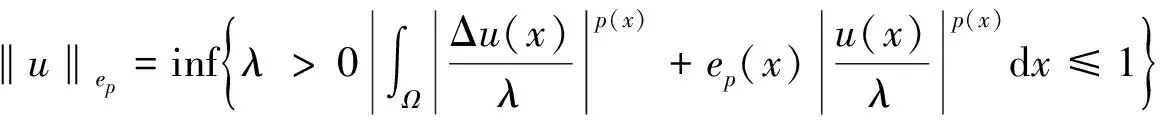

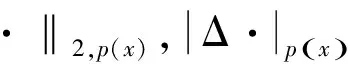
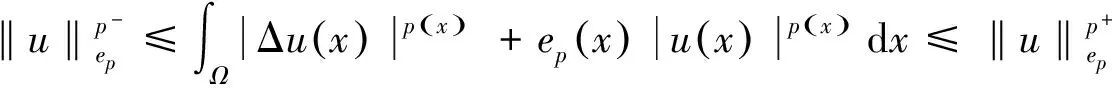
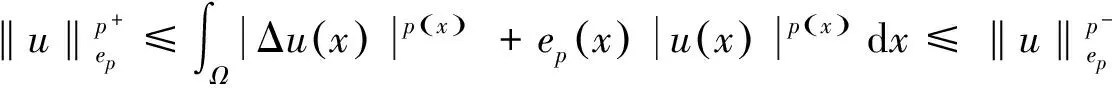


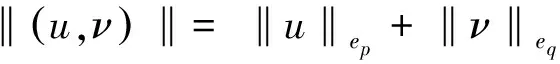
2 主要结果