基于混沌振子的滚动轴承复合故障诊断

刘 燕，胡学青

宿州学院煤矿机械与电子工程研究中心，安徽宿州，234002

基于混沌振子的滚动轴承复合故障诊断

刘 燕，胡学青

宿州学院煤矿机械与电子工程研究中心，安徽宿州，234002

针对强噪声背景下的信号难于检测的问题，结合滚动轴承振动信号的非平稳以及非线性特点，提出了一种用Duffing阵子结合欧氏距离检测滚动轴承复合故障诊断的方法。该方法采用欧氏距离确定混沌振子由混沌状态向大尺度周期状态转换的临界阈值，利用欧氏距离的跃变自动识别混沌振子的状态。并仿真推导出了待测信号频率和混沌振子阈值之间的关系，很好地解决了由于实际故障频率的误差导致结果不准确的问题，该方法成功地应用在滚动轴承的早期模拟复合故障中，取得了较好的效果。

复合故障；混沌振子；欧式距离；临界阈值

滚动轴承在运行过程中经常会受到损伤，出现故障，轴承故障信号都是非线性非平稳的。传统的信号处理技术分析处理的都是线性平稳的信号，对非线性信号的处理是将其转化为线性信号进行处理，往往会丢失非线性信号里一些重要的状态特征。当工厂中噪声背景复杂，故障信息容易被随机噪声及其他零部件振动信号淹没，尤其当轴承存在早期微弱故障时，利用传统信号处理方法较难提取。混沌振子检测法是近年来发展起来的一种新的非线性特征提取方法。文献[1]提出了一种基于局域波和混沌振子的微弱信号检测方法，并对转子系统早期碰磨故障信号进行检测，结果说明了该方法的有效性。文献[2]提出将传统时域方法互相关结合李雅普诺夫指数的微弱正弦信号混沌检测方法，该方法能有效地检测出强噪声背景下的微弱正弦信号。文献[3]提出了利用混沌振子来解调强噪声中幅移键控(ASK)信号的新方法，并提出利用功率谱熵判别系统状态的新方法。该方法实现了对ASK信号的解调，且抗噪性能优于传统的解调方法。本文提出了一种基于混沌振子和欧氏距离相结合的微弱信号检测方法，并将该方法应用于深沟球轴承的内圈和外圈复合故障中，取得了很好的效果。

1 混沌振子

混沌振子检测可以通过Homels型Duffing方程[4]建立，这是一个二阶微分方程，方程形式如下：

x+kx-x3+x5=fcos(t)

(1)

其中k为阻尼比，取k=0.5；-x3+x5为非线性恢复力；fcos(t)为内置信号。

计算步长h=0.04，数据长度n=4 000，信号频率ω=1，对式(1)进行离散化并采用4阶Runge-Kutta法进行求解。当f=0时，系统行为在相平面表现为鞍点(0,0)和焦点(±1,0), 初始条件的不同，系统呈现的状态也不同，但是最终将收敛到两焦点中的一个，如图1所示。

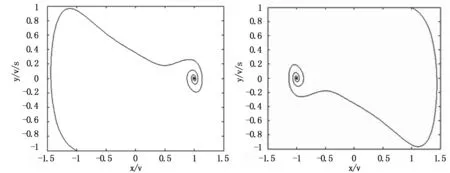
图1 不同初始值的Duffing振子相图

改变策动力f的值，其他参数不变，使f从0逐渐增加到阈值fa，系统将经历3个状态，分别为同宿轨道、倍周期分叉、混沌状态。fa的值是由Melnikov方法计算确定。继续增加f的值，当大于另一阈值fb时，系统的状态从混沌过渡到大尺度周期状态，如图2所示。

图2 Duffing振子运动相图

从图2可知，区分混沌状态和大尺度周期状态的临界阈值fb=0.729 4，当内置信号幅值f=fb时，系统处于混沌临界状态；一旦信号幅值f>fb，系统过渡到大尺度周期状态，fb即为混沌振子的阈值。在本文中采用欧氏距离方法定量观察混沌振子运动形态，此种方法直观又可靠。

令t=ω0τ，可以推出任意频率的周期信号的检测数学模型[5]：

(2)

当加入外部周期信号时，式(2)变为：

(3)

式中,ω0为内部周期信号的角频率,ω1为待测周期信号的角频率，θ为待测周期信号的相位，N(t)为随机噪声[6]。

2 混沌振子相位图的定量识别

应用混沌振子检测微弱信号，可以通过观察系统的相图变化判断系统是否含有待检测频率，从而可以实现早期故障的检测。文献[7]应用二维近似熵观察混沌振子相图的变化，取得了不错的效果。文献[8]利用Hu矩识别混沌振子阈值，可以实现自动检测混沌振子相图状态。本文采用欧氏距离定量度量混沌振子的阈值，成功地将混沌振子应用在早期微弱故障信号检测上。欧氏距离就是不同状态下的相位图上各点到原点(0,0)的距离。欧氏距离用L表示：

(4)

式中，N点的个数，即采样点数；xk，yk分别是相位图上第k个数据对应的横坐标和纵坐标。

设待测信号：s(t)=0.05cos(2π·40·t)

(5)

将待测信号代入式(3)得：

(6)

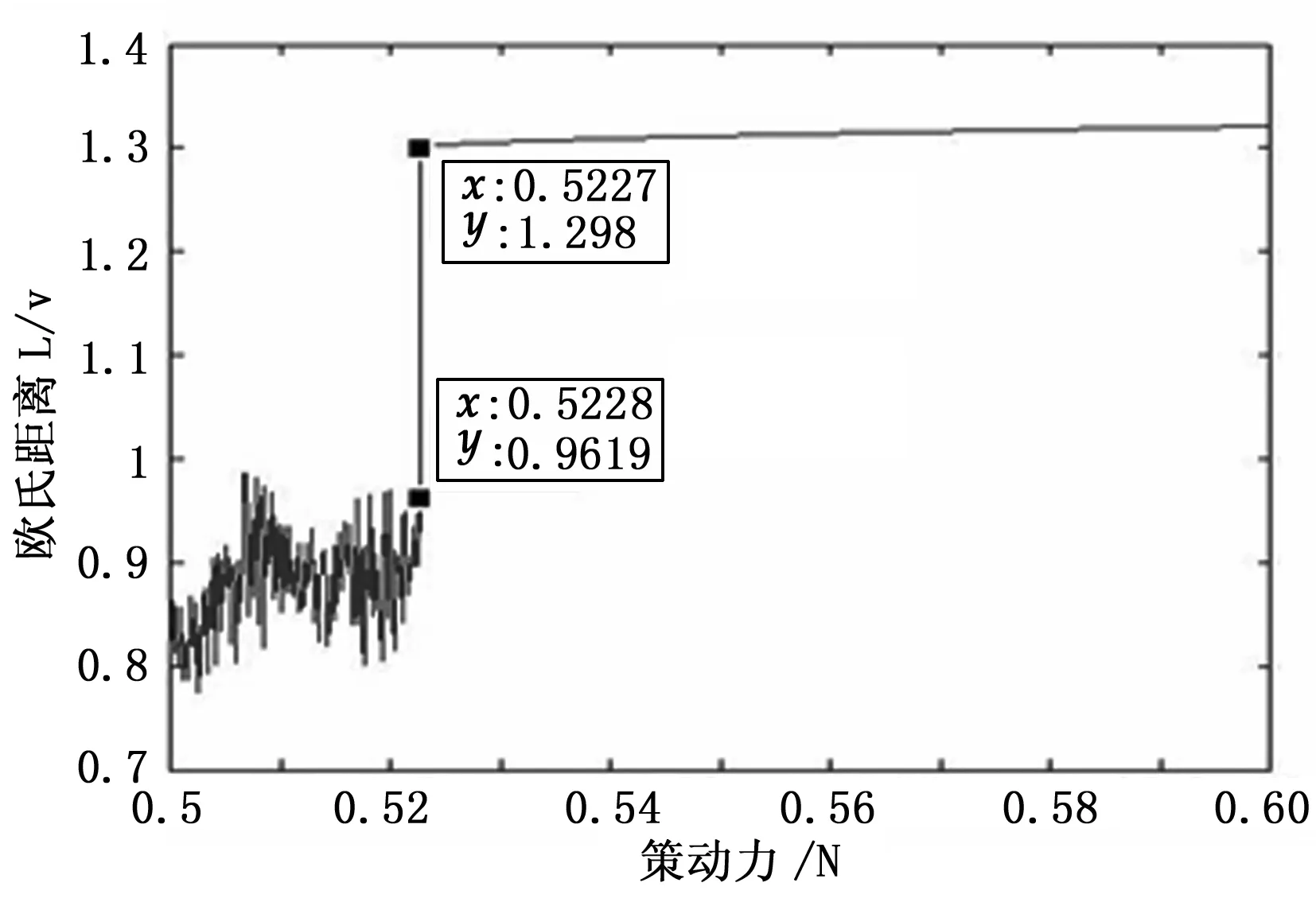
图3 欧氏距离L随策动力f变化的趋势图

首先，对式(6)采用4阶Runge-Kutta算法进行求解，取初始值x(0)=1，y(0)=1，k=0.5，数据长度N=9 216，采样频率fs=4 000。逐步增大策动力f的值，欧氏距离的值同时发生变化，如图3所示。从图3可知，f=0.522 6和f>0.522 6，欧氏距离的取值有很大范围的波动，所以fb=0.522 6是混沌振子的阈值。

其次,设置f=0.5，因为f+0.05>0.522 6，所以混沌振子脱离混沌状态，从系统输出的相轨迹图检测已知频率的微弱信号，如图4所示。

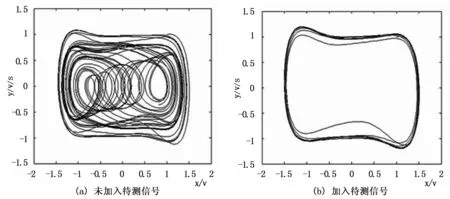
图4 不同状态下的混沌振子相图

当初始值x(0)=1，y(0)=1，k=0.5，数据长度N=9 216，采样频率fs=4 000。待测频率为40.2-42(步长为0.2)Hz的幅度增加，混沌振子的阈值也呈现一定的规律。

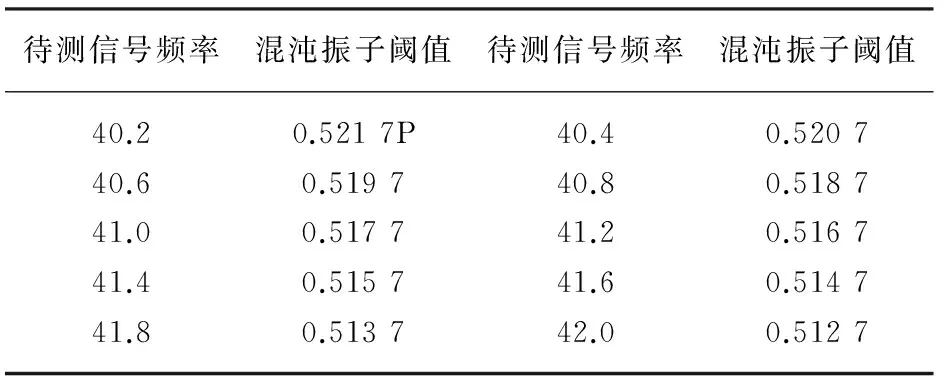
表1 阈值变化规律

从表1中可以看出，频率每增加0.2 Hz，阈值减少0.000 1，前提是采样频率不变。如果采样频率改变，步长因此会改变，从连续系统导出的离散系统也不同，这样阈值的变化呈现另一种规律。目前，阈值的变化和频率变化还没有一个更深的理论推导，有待研究。验证如下：初始值x(0)=1，y(0)=1，k=0.5，数据长度N=9 216，采样频率fs=4 000。待测频率ω=45 Hz，仿真得到阈值fb=0.497 9，按照上面规律得到fb=0.497 7，阈值误差只有0.000 2，说明仿真推导准确度很高。

3 基于混沌振子的故障分析

实验轴承型号是6311深沟球轴承，轴承各参数如表2所示。

表2 轴承各参数

通过SG双色金属刻字机来模拟轴承外圈和内圈的早期点蚀故障，加工的故障直径大小约为0.5 mm,深度大小为几十微米。使用便携式采集仪采集故障信号，将振动信号导入至MATLAB，其时域波形和幅值谱如图5所示。采样频率设为12 800 Hz，在主轴转速为1 800 r/min下，根据表2中轴承各参数，计算出轴承内圈故障频率为fi=153.243 Hz，外圈故障频率f0=94.75 Hz。

图5 实测信号的时域波形及幅值谱

从图5(c)的局部放大图中发现频率和故障频率差距很大，用傅里叶变换测试不出故障频率。下面用混沌阵子对该信号进行分析。

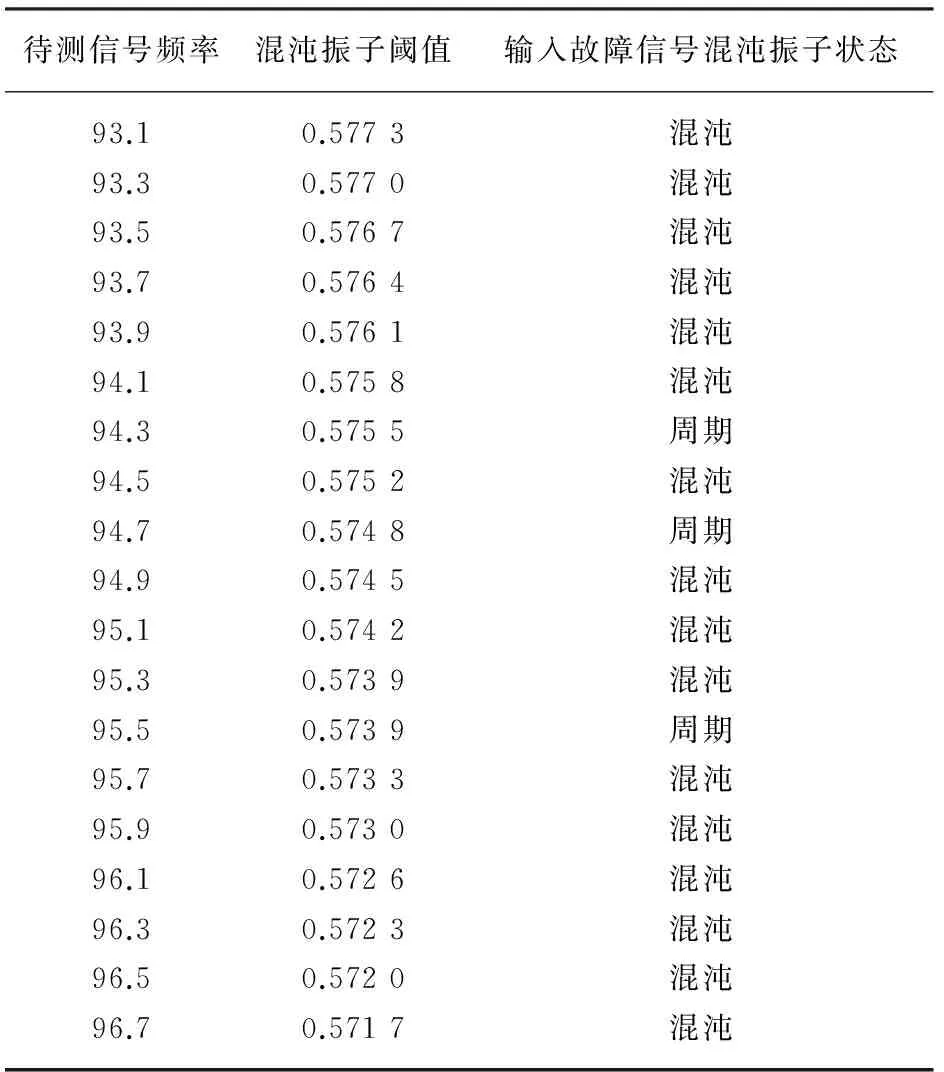
表3 外圈故障频率检测结果

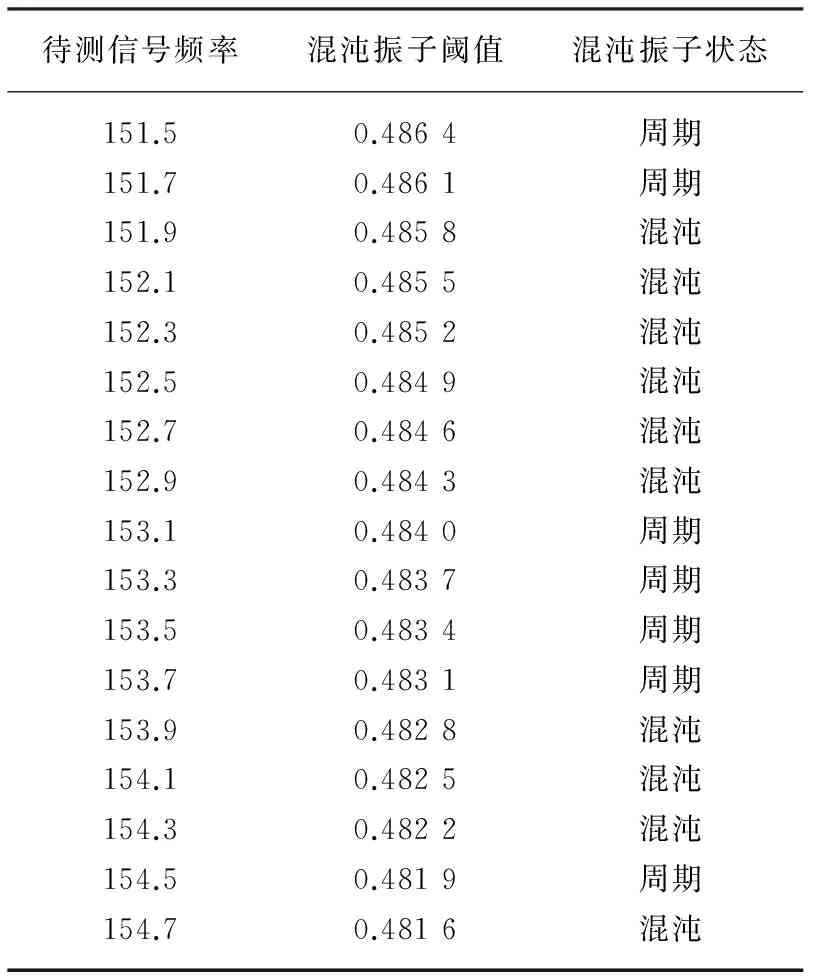
表4 内圈故障频率检测结果

由于加工误差的影响，故障频率不可能计算得那么精确。首先，设置策动力频率ω0=2×π×fi，内圈故障频率的取值fi为93.1-96.7(步长为0.2)，检测结果如表3所示。

检测内圈故障方法和外圈一样，首先设检测频率ω0=2×π×f0，内圈故障频率的取值f0为151.5-154.7(步长为0.2)，检测结果如表4所示。

4 结束语

利用欧氏距离的跃变可以定量识别混沌振子状态，仿真推导出待测信号频率和混沌振子临界阈值之间的关系，并验证了仿真的准确性。本文将基于混沌振子非线性方法应用于滚动轴承的复合故障诊断中，取得了很好了效果。该方法可以作为早期微弱周期信号检测的一种方法。

[1]王凤利,段树林,于洪亮,等.基于局域波和混沌的转子系统早期碰摩故障诊断[J].大连海事大学学报，2008,34(3):85-88

[2]陈伟根,云玉新,杜林，等.基于互相关和李雅普诺夫指数的微弱正弦信号[J].混沌检测电力系统自动化,2008,32(18):44-48

[3]高清山,张天骐,蒋世文，等.基于混沌振子的微弱ASK信号解调[J].电子技术应用, 2010,24(4):104-109

[4]刘秉正,彭建华.非线型动力学[M ].北京:高等教育出版社,2004：55-302

[5]王冠宇,陶国良．混沌振子在强噪声背景信号检测中的应用[J].仪器仪表报,1997,18(2):209-212

[6]Wang Guan Yu,Wei Zheng,He Sailing.Estimation of amplitude and phase of a weak signal by using the property of sensitive dependence on initial conditions of a nonlinear oscillator[J].Signal Processing,2002,82(1):103-115

[7]李强，王太勇，胥永刚，等.基于混沌和二维近似熵的滚动轴承故障诊断[J].振动工程学报,2007,20(03):268-273

[8]马海龙.复杂机电设备微弱特征提取与早期故障诊断方法研究[D].北京:北京工业大学机械工程与应用电子技术学院，2011：1-119

(责任编辑：汪材印)

Multi-fault Diagnosis for Roller Bearings Based on Chaotic Oscillator

LIU Yan，HU Xueqin

Mechanical and Electronic Engineering Research Center for Coal Mine Suzhou University,Suzhou，234002

Due to the faut that the useful signals are often buried in heavy noise and difficult to be detected and the fact that vibration signal for roller bearings is non-stationary and time-variation,a new weak signal detection method based on the chaotic oscillator and the euclidean distance is proposed.The Euclidean distance is adopted to ascertain the threshold value of the chaotic oscillator from the chaotic status to the large-scale cycle.And the simulation is derived for the relationship between the measured signal frequency and chaotic oscillator threshold.It is asatisfactory solution to the error due to the fault frequency leading to the inaccuracy of the result，and is successfully applied to the combine fault of the deep grove ball bearing.

combine fault；chaotic oscillator；euclidean distance；threshold value

10.3969/j.issn.1673-2006.2015.02.024

2014-10-11

宿州学院煤矿机械与电子工程研究中心开放课题“矿山机械轴承的复合故障早期信号检测”(2014YKF16 )。

刘燕(1987-)，女，安徽宿州人，硕士，助教，主要研究方向：设备故障诊断。

TH133.3

A

1673-2006(2015)02-0092-04