跨孔法测试阻尼比的几个问题

韩绍英

(中核辽宁核电有限公司,辽宁 葫芦岛 125100)

跨孔法测试阻尼比的几个问题

韩绍英

(中核辽宁核电有限公司,辽宁 葫芦岛 125100)

阻尼比是抗震设计中要用到的一个岩土参数，阻尼比的测试方法大致有激振法测试(包括强迫振动和自由振动两种)、振动三轴和共振柱测试等几种。本文简述了阻尼比及衰减系数的物理概念，针对《岩土工程试验监测手册》中提出的跨孔法测试阻尼比的公式进行了推导，指出了手册中公式存在的错误，对跨孔法测试阻尼比的方法优缺点进行了分析；指明了跨孔法测试存在的问题，其实用性需要进一步考证。

阻尼比；对数衰减率；衰减系数；跨孔法

1 阻尼比测试方法

阻尼比是抗震设计中要用到的一个岩土参数，设计院往往要求在初步设计或更早的阶段，岩土工程勘察单位就能提出这个参数，以供前期设计计算使用。

在国家或行业规范中，阻尼比的测试方法大致有激振法测试[1](包括强迫振动和自由振动两种)、振动三轴和共振柱测试等几种，这几种方法各有优缺点：激振法测试是一种原位测试方法，有完善的理论基础，除地基阻尼比参数外，还可以提供动力机器基础的地基抗压、抗剪和抗扭刚度系数，地基竖向、水平回转向以及扭转向参振质量等动力特性参数，原位测试方法地基岩土体能够保持原有状态，不会受到扰动，故测试得到的参数可靠性较高，但测试前需要专门加工混凝土块体，使用专门的激振器和测试仪器，成本相对较高，且测试只能在室外地表进行，如果需要深层地基岩土体的参数，这个方法无法实现。振动三轴和共振柱测试均属于室内试验，操作简单易行，但均存在试样采取过程中的扰动问题，测试结果往往会失真，有的地层则无法取得原状试样。

《岩土工程试验监测手册》(林宗元主编，1994.12)(以下简称《手册》)[2]中提供了另外一种原位测试的方法—跨孔法波速测试岩土体阻尼比的公式，本文对其进行探讨。

2 手册中的方法存在的问题

跨孔法波速测试是一种常用的原位测试方法，《手册》中提供了跨孔法测试岩土体阻尼比的方法。如图1所示，在一定间距的三个钻孔的同一标高，一端的钻孔中使用电火花或其他振源激发振动，使用地震检波器或声波换能器在另两个钻孔中接收，由接收到的波的振幅、频率，可以确定岩土体的阻尼特性，公式如下：

α=ln((A1R1/A2R2)/(R2-R1))

(1)

式中：α为衰减系数；R1、R2为检波点至振源的距离，m；A1、A2为分别为R1、R2处波形记录上同相位点的振幅值，m。

(2)

式中：δ为对数衰减系数；V为体波速度，m/s；f为波的频率，Hz；λ为波长，m。

(3)

式中：Dz为阻尼比。

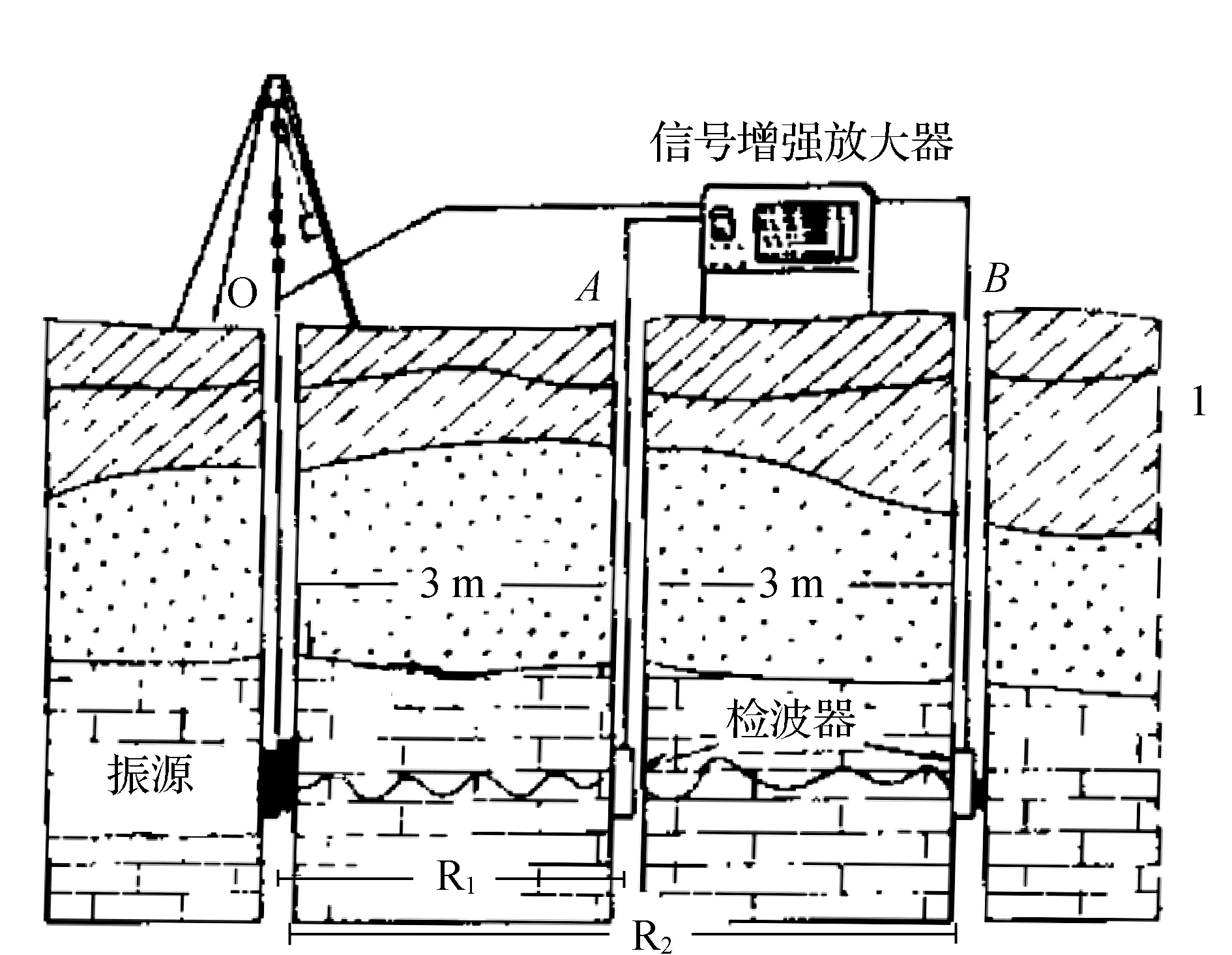
图1 跨孔法波速测试示意图

以上公式，将地震波动理论中的衰减系数α与机械振动理论中的对数衰减系数δ建立了联系，进而由对数衰减系数计算得到阻尼比参数。

笔者认为，在这种方法的测试及参数计算中，均存在一些问题。

(1)测试本身存在的问题

首先，跨孔波法测试一般使用地震仪(或动测仪)及三分量地震检波器。测试仪器经检定合格后，利用检波器测试波的传播速度是准确的。三分量检波器探头在一个容器内安装了灵敏方向相互垂直的三个地震检波器，检波器本身是不需要标定的，也无法进行标定(灵敏方向无法确定)，因此质点振动的振幅无法准确测量，由两孔同一标高的两个测试波形读出的质点振幅只能进行定性的比较。

其次，三分量检波器在孔内的摆置方向是随机的，其接收波的灵敏方向不受控制，由两个探头接收激发孔同一振动时，检波器的灵敏方向不能保证指向波的传播方向，因此即使两个接收检波器的灵敏度是一样的，测试仪器接收到的两个检波器位置质点振幅的比值能否准确代表地震波能量的衰减，也值得商榷。

为了消除传感器接收的方向性问题，阻尼比跨孔法测试时可使用声波换能器接收地震波信号。两个圆筒形的声波换能器接收水平方向同一标高来自振源的声波信号，可以不用考虑波的传播方向与传感器接收方向是否一致的问题，但声波换能器同样是不做标定的，测试时只能使用同批次出厂的、同一批号的声波换能器，以求灵敏度大致相同，并在测试前对换能器灵敏度的一致性进行有效的检验。

(2)参数的计算中存在问题

一是地震波传播的衰减系数α的计算公式有误；二是地震波传播的衰减系数α与机械振动的对数衰减系数δ之间的联系缺乏充分的理论依据。下文对此进行详述。

3 机械振动理论及阻尼比的定义

根据机械振动理论，质量m、弹性k和阻尼c是一个振动系统力学模型的三要素。具有黏性阻尼的质量弹簧系统的自由振动的微分方程为

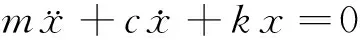
(4)

它的通解为：

x=Aeλ t

(5)

将式(5)代入式(4)，得到系统的特征方程为

mλ2+cλ+k=0

(6)

求解特征方程式(6)，得到特征值为

(7)

式(7)中根式值为零的阻尼系数c定义为临界阻尼系数cc，即：

(8)

式中：ωn为无阻尼固有角频率，为

(9)

(10)

为了便于阻尼参数分析，引入阻尼比ξ，同Dz,即

(11)

自然界中岩石和土体的振动均为欠阻尼状态，即ξ<1，见图2，此时，特征值为

(12)

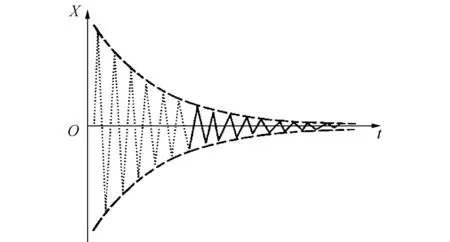
图2 欠阻尼响应(ξ<1)

因此，对数衰减系数δ与系统的阻尼比ξ之间有下列关系。

(13)

由式(13)得

(14)

(15)

当阻尼比ξ很小时，有

(16)

综上所述，岩土体中质点的振动幅值呈指数衰减，岩土体阻尼比远小于1，其值与对数衰减系数δ(相邻振幅比的自然对数值)的关系如式(15)。根据这种关系，《地基动力特性测试规范》(GB/T 50269-1997)[3]中，规定了自由振动法测试地基竖向阻尼比的方法。

4 《手册》中跨孔法测试阻尼比公式的推导

4.1 衰减系数的计算

如图1所示，在跨孔法测试时，振源与接收换能器按图示方式布置，图中O为振源，A、B为接收换能器，分别距振源R1和R2，在不考虑透射损失和界面散射时，按球面波计算,A收到的信号的振幅为

(17)

B收到的信号的振幅为

(18)

上两式等号两边相除

(19)

因此

(20)

两边取自然对数，则衰减系数为

(21)

即:

α=ln(A1R1/A2R2)/(R2-R1)

(22)

手册中的公式为：

α=ln((A1R1/A2R2)/(R2-R1))

即公式(1)中多了一个括号，应该是排版时的失误。

4.2 阻尼比的计算

得到衰减系数后，剩下的问题是将机械振动的对数衰减率δ和地震波传播的衰减系数α建立联系。手册中公式的思路是：机械振动的对数衰减系数δ是有阻尼质量弹簧体系自由振动相邻振幅比的自然对数，反映的是一个周期内质点振幅的衰减程度，同时对应着地震波传播一个波长的振幅衰减，也就是说对数衰减系数δ等于衰减系数乘以波长，即

(23)

得到对数衰减率δ后，就可以利用式(15)计算阻尼比ξ。

5 《手册》中跨孔法测试阻尼比的问题

以上介绍了《手册》中跨孔法测试地基岩土体阻尼比的方法，除了《手册》中计算衰减系数的公式有误外，笔者认为该方法还存在以下问题。

(1)机械振动振幅随时间的衰减与地震波振幅随传播距离的衰减是不是有式(23)的严格相关的关系，值得商榷。

在国家和行业规范中[3-5]，根据阻尼比和衰减系数的物理定义，分别规定了各自的试验方法，但均未提及机械振动的阻尼比与地震波传播的衰减系数之间有什么固有的相关关系。

如在《地基动力特性测试规范》(GB/T 50269-1997)[3]中，规定了阻尼比的测试方法大致有激振法测试(包括强迫振动和自由振动两种)、振动三轴和共振柱测试等几种，这几种试验均是根据阻尼比的物理定义：介质阻尼系数与临界阻尼系数之比，利用有阻尼单自由度质量弹簧系统受迫振动理论(强迫振动激振法测试)、有阻尼单自由度质量弹簧系统自由振动理论(自由振动激振法测试、共振柱测试)、受迫振动时能量衰减与峰值能量的关系：应力—应变滞回圈面积与相应三角形面积之比(振动三轴测试)等理论，测试岩石和土的阻尼比参数，所依据的公式均可由相关理论推导得出。

在《地基动力特性测试规范》(GB/T 50269-1997)[3]中，同时规定了一种衰减系数的测试方法：振动衰减测试，该方法利用波在半无限空间介质中传播时，由波前扩散和介质吸收引起地震波振幅衰减的特性，根据衰减系数的物理定义，在距振源不同距离分别放置测振传感器，根据各测点振幅与距振源距离的关系，计算衰减系数值。

在其他一些行业规范中，也有利用声波法测试岩石衰减系数的方法，均是利用了波的振幅与距振源的距离的关系，根据衰减系数的物理定义计算该参数，但该参数与阻尼比的关系目前尚无成熟的理论支持。

(2)自然界的岩体中多存在大大小小的节理裂隙，属不均匀介质，跨孔法测试中，地震波从振源到接收点能量的衰减因素有几何扩散、介质吸收、介质存在节理裂隙时的透射、反射及折射损失等，前两者体现在了计算公式中，后者则无法估计。按《手册》公式计算衰减系数时，两个接收点振幅的衰减包含了上述几个方面的影响，而不单纯是几何扩散和介质吸收的因素，因此计算得到的衰减系数即包含了能量随距振源距离指数衰减的介质吸收因素的影响，又包含了由于存在节理裂隙造成的不均匀介质的透射、反射及散射等因素的影响，与理论上的衰减系数还是有所差别的。

(3)跨孔法测试的是速度或加速度信号，阻尼比计算使用的是位移值，稳态响应时，各物理量的比值是相等的，自由振动时则存在一定误差。

6 结 语

阻尼比是机械振动理论中定义的参数，反映的是机械振动中能量随时间的衰减特性；衰减系数则是地震波理论中定义的参数，反映的是波在传播过程中能量随传播距离的衰减特性，二者存在一定的相关性，但是否有绝对的相关关系，需要进一步考证。

跨孔法测试阻尼比时，应考虑传感器的灵敏度和接收方向问题。使用同批次出厂的、同一批号的声波换能器，可以大致满足方向性和灵敏度的要求，但在测试前应对换能器灵敏度的一致性进行检验。

《手册》中跨孔法测试地基岩土体阻尼比的公式有误，使用时应注意纠正。

[1] 中华人民共和国建设部.GB 50021-2001岩土工程勘察规范[S].北京：中国建筑工业出版社，2009.

[2] 林宗元.岩土工程试验监测手册[S].沈阳：辽宁科学技术出版社，1994.

[3] 国家技术监督局，中华人民共和国建设部.GB/T 50269-1997地基动力特性测试规范[S].北京：中国标准出版社，1998.

[4] 中华人民共和国住房和城乡建设部.GB 51041-2014核电厂岩土工程勘察规范[S].北京：中国计划出版社，2015.

[5] 中华人民共和国水利部.SL 264-2001水利水电工程岩石试验规程[S].北京：中国水利水电出版社，2001.

Questions of damping ratio derived from cross-hole wave velocity test

HAN Shaoying

(CNNPLiaoningNuclearPowerCo.,Ltd.,Huludao125100，China)

As a geotechnical parameter, damping ratio is inevitably used in seismic design. There are several main methods for testing damping ratio, such as shock excitation test method (including forced vibration and free vibration), dynamic triaxial and resonant column test methods etc. This paper presented the introduction of the physical conception of damping ratio and attenuation coefficient. Therefore, the author utilized the analytic derivation to analysis the formula of the cross-hole wave velocity test used for testing damping ratio in geotechnical testing and monitoring manual. Finally, the author pointed out the existing mistakes of the formula, simply described the physical concept of attenuation coefficient and analyzed the advantages and disadvantages of the method of cross-hole wave velocity test of damping ratio. As for the problems existing in the method of cross-hole wave velocity test, their practicability is still needed to be further studied and confirmed.

damping ratio；logarithmic decrement ratio；attenuation coefficient； cross-hole wave velocity test

韩绍英(1971-)，女，高级工程师，从事水文地质与工程地质专业研究与设计工作。E-mail：hsy3877@126.com

TU435

A

2096-0506(2015)06-0039-04