基于势概率假设密度平滑器的多目标跟踪算法
2015-06-23谢兴祥蔡如华吴孙勇闫青竹
谢兴祥,蔡如华,吴孙勇,闫青竹
(桂林电子科技大学数学与计算科学学院,广西桂林 541004)
基于势概率假设密度平滑器的多目标跟踪算法
谢兴祥,蔡如华,吴孙勇,闫青竹
(桂林电子科技大学数学与计算科学学院,广西桂林 541004)
针对概率假设密度(PHD)滤波在杂波环境下对机动多目标进行检测与跟踪时,易出现高阶势分布信息丢失,从而导致目标检测出现偏差的问题,提出一种将势概率假设密度(CPHD)滤波与平滑算法相结合的多目标跟踪算法。从CPHD的预测与更新步骤出发,结合后向平滑递归公式,推导CPHD平滑公式,并提出基于高斯混合实现的GM-CPHD平滑器。仿真实验表明,GM-CPHD平滑器的检测与跟踪性能优于未经平滑处理的CPHD滤波器。
概率假设密度;势概率假设密度;高斯混合;平滑器
Mahler于2003年在研究多目标贝叶斯递归问题时提出概率假设密度(probability hypothesis density,简称PHD)滤波[1],该滤波是解决传统多目标跟踪问题的一种有效方法,它通过传播多目标后验概率密度的一阶矩来近似多目标跟踪问题的最优解,可应用于目标数未知的多目标跟踪问题[2]。其明显优势是避免了直接计算后验概率密度函数,且无需关联复杂的数据便可从量测数据中估计目标数目和提取目标状态。Vo等[3-4]给出了PHD滤波的粒子滤波实现(SMC-PHD)和高斯混合实现(GM-PHD)。但在杂波环境下对多个运动目标进行检测与跟踪时,由于PHD滤波假设目标数服从泊松分布,仅利用一阶矩统计信息对目标数目进行估计,易出现高阶势分布信息丢失,从而限制了其跟踪性能,导致对目标的估计出现偏差,当目标数目较多时,这个偏差会更大。为解决此问题,Mahler在PHD滤波基础上提出势概率假设密度(cardinalized probability hypothesis density,简称CPHD)滤波[5-6]。CPHD滤波是一种广义的递归PHD滤波,能够联合传播后验强度函数和后验势分布函数,根据物理空间描述法推导出CPHD滤波的具体实现公式[7]。
文献[8]在多目标跟踪问题中对CPHD滤波进行高斯混合实现,性能比传统的PHD滤波要好,但计算仍十分复杂。Nandakumaran等[9-10]引入了平滑概念,其中文献[9]根据PHD滤波提出基于粒子滤波实现的平滑算法,但其计算过程中需要大量粒子,增加了计算量,耗时多;文献[10]对PHD平滑算法进行高斯混合实现,提出GM-PHD平滑算法,并在二维场景中对线性高斯模型进行仿真实验,结果显示,虽然检测目标有滞后现象,但性能要比未经平滑处理的GM-PHD滤波器好。鉴于此,将PHD滤波扩展到CPHD滤波,基于文献[10-11]推导出CPHD后向平滑递归公式,并将其进行高斯混合实现,得到GM-CPHD平滑器,有效地减少了计算量。
1 问题描述
考虑目标在一个二维运动场景中运动,目标的状态方程和量测方程分别描述为:
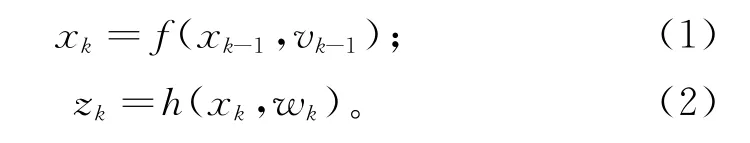
其中状态模型f(·,·)和量测模型h(·,·)均为已知。根据量测方程,累积直到时刻k的量测序列Z1:k,然后从该序列中估计出目标数目和目标状态。
Vo等在随机有限集(RFS)理论的基础上将多目标跟踪问题表述为对多目标状态Xk和量测Zk的滤波问题[4]。其中Xk为时刻k多个目标状态的集合, Zk为时刻k多个目标量测的集合,分别记为:

不考虑衍生目标,通过Xk、Zk所建立的模型描述一个多目标跟踪系统,有
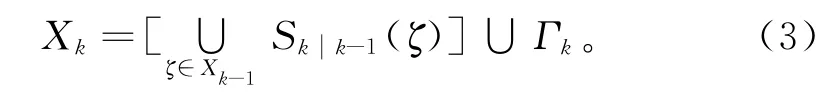
其中:Skk-1为存活目标RFS;Γk为自发出生目标RFS。

其中:Kk为杂波集;Θk为一个目标产生的量测。
上述多目标跟踪滤波问题可表述为寻找一个最优多目标后验概率密度问题。假设时刻k-1的多目标后验概率密度pk-1(·Z1:k-1)已知,则时刻k的多目标后验概率密度可通过多目标贝叶斯递归公式求得,
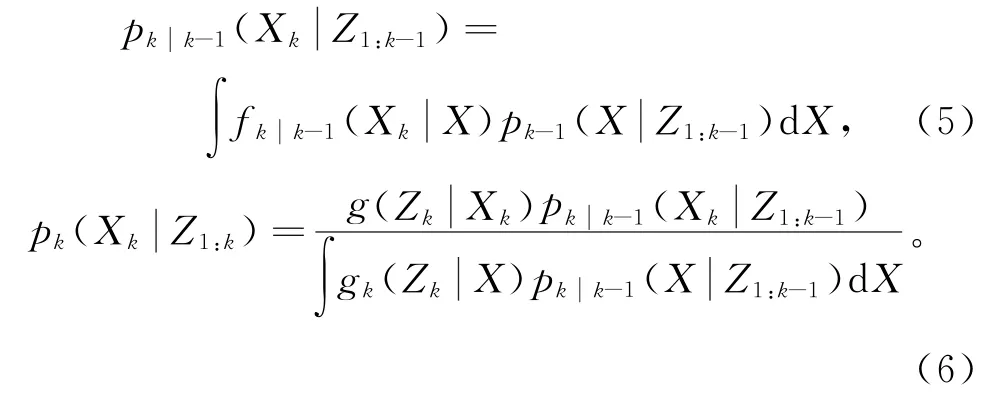
其中:fkk-1(XkX)为多目标马尔可夫状态转移概率密度函数;gk(ZkX)为似然函数。
平滑器包括前向滤波和后向平滑两方面的内容[12],因此平滑器实际上应称为“先前向滤波,接着后向平滑的平滑器”,简称“前向-后向平滑器”。前向滤波是指后验概率密度通过贝叶斯递归公式向前传播到时刻k,由CPHD递归公式执行;后向平滑是指平滑后的后验概率密度通过后向平滑递归公式[13]从时刻k向后传播到时刻t(k>t),后向平滑递归公式可通过有限集统计学和点过程理论推导得到。在多目标跟踪问题中,前向滤波的后验概率密度通过多目标贝叶斯递归公式(5)和(6)向前传播到时刻k;而在后向平滑中,平滑后的后验概率密度通过后向平滑递归公式(7)从时刻k向后传播到时刻t,
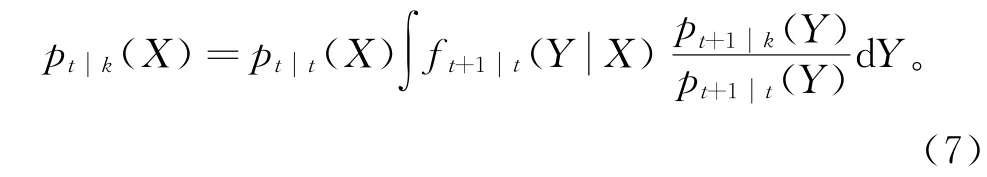
与多目标贝叶斯递归公式(5)和(6)传播多目标后验概率密度函数不同,CPHD递归公式传播的是多目标后验强度函数vk(x)。后验强度比后验概率密度更适合对目标进行检测和跟踪,因此利用CPHD递归公式替换式(5)和(6)计算多目标后验强度,使得计算简化,并且从CPHD的预测与更新步骤出发,结合后向平滑递归公式(7),可推导出CPHD后向平滑递归公式。
2 GM-CPHD平滑器
2.1 CPHD滤波器
Mahler在PHD滤波的基础上提出CPHD滤波[1],其在传播PHD函数的同时也在传播后验势分布(目标数)概率密度函数。
CPHD预测步[8]:
1)预测势分布为
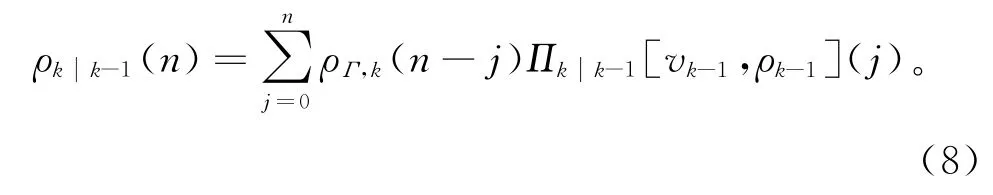
2)预测强度为
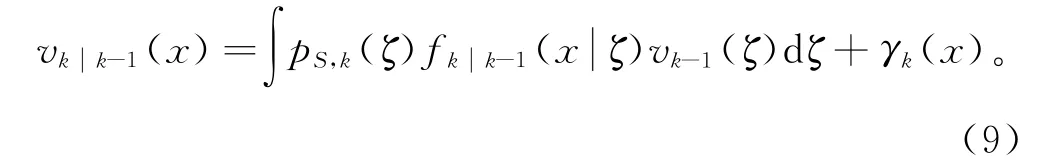

pS,k(ζ)为时刻k目标存在概率;fkk-1(·ζ)为时刻k的单一目标转移密度;γk(·)为时刻k自发出生目标强度;ρΓ,k(·)为时刻k自发出生目标势分布。
CPHD更新步:
1)更新势分布为

2)更新强度为

其中:

Zk为时刻k的量测集;gk(·x)为时刻k单一目标的量测似然函数;pD,k(x)为时刻k的目标检测概率;κk(·)为时刻k杂波量测强度;pK,k(·)为时刻k杂波势分布。
1.2 临床资料收集方法 通过病历登记资料以及询问家属等方式获得受试早产儿(脑瘫组以及对照组)的基本信息。基本信息包括受试早产儿的基本情况以及脑瘫患儿存在哪些伴随症状等。
2.2 GM-CPHD平滑器的推导
结合文献[7]、[10-11],推导并得到CPHD后向平滑递归公式:

其中:t=k-1,k-2,…,k-L(k>t);L为平滑算法的滞后时间;vtt为t时刻CPHD滤波的强度函数;vtk、vt+1k分别为t、t+1时刻的CPHD平滑强度函数;vt+1t为t+1时刻CPHD滤波的预测强度函数。平滑公式中有积分运算,会导致计算十分复杂,因此运用高斯混合实现方法,将积分运算变为高斯分布下的求和运算。
CPHD滤波的高斯混合实现依赖于有关单一目标转移和量测模型以及目标出生、死亡和检测的假设。
假设1 每个目标都服从线性高斯动态模型,即

且其传感器的线性高斯量测模型为
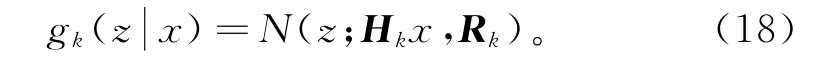
其中:Ν(·;m,P)为以m为均值、P为协方差的高斯密度分布;Fk-1为状态转移矩阵;Qk-1为过程噪声协方差;Hk为观测矩阵;Rk为观测噪声协方差。
假设2 多目标的势分布服从高斯分布,

假设3 目标存活概率与目标检测概率相互独立:
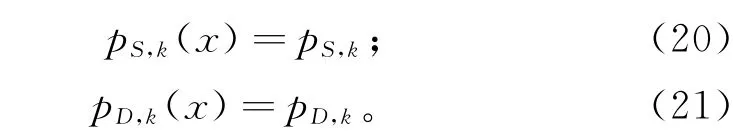
假设4 目标出生RFS集的强度是高斯混合形式,

基于以上4个假设,假设在k时刻,CPHD滤波的预测强度vkk-1、预测势分布pkk-1(n)、更新强度vk(x)及更新势分布pk(n)都已给定,且有:

则可得在t时刻和t+1时刻的CPHD更新强度分别为:

将式(25)、(26)代入CPHD后向平滑递归公式(16),整理后得:
式(27)中仍然包含积分运算,使得计算十分复杂,为此将积分中的用高斯混合形式式(17)替代。该高斯混合形式可看做一个平滑器的实现,且该平滑器具有相对应高斯分量的均值和方差,因此可得到:
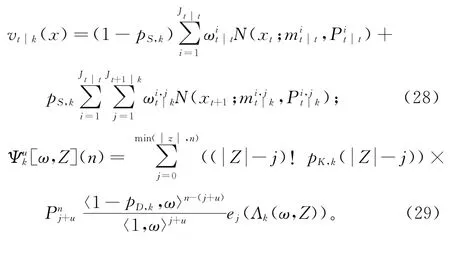
其中:

高斯混合分量的权重为:
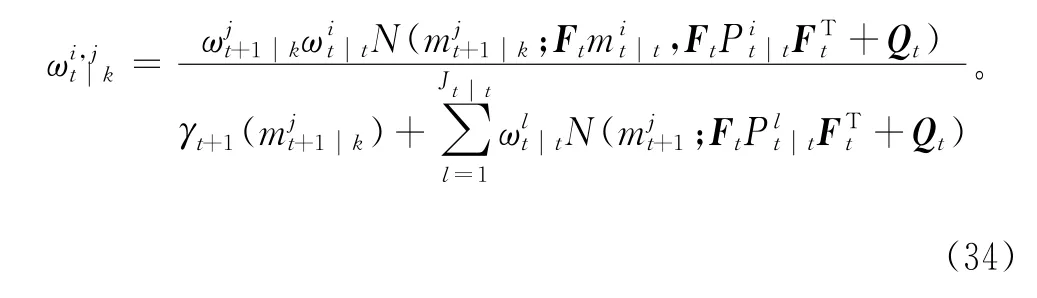
式(28)即为GM-CPHD滤波器的平滑公式。
在对后验强度vk(x)用高斯混合形式表示时,多目标状态的提取比PHD滤波的粒子滤波实现算法容易,因为构成高斯分量的均值实际上是后验强度vk(x)的局部极大化值,但此时需利用“修剪”技术去除高斯混合形式中含有较低权重和方差的高斯分量,并利用“合并”技术将比较密集的高斯分量进行合并,当从个后验强度vk(x)中提取多目标状态时,便可得到较近似的状态估计值。与高斯混合强度vtk(x)相应的目标期望数可通过对目标权重求和得到,
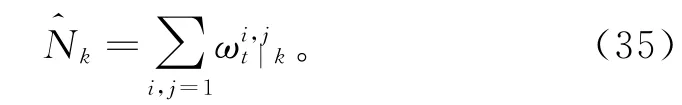
3 数值仿真实验与分析
3.1 实验评价指标
采用最优子模式分配(optimal sub-pattern assignment,简称OSPA)度量作为仿真实验的评价指标。OSPA度量是指对2个有限集中的点进行分配并求出这些点之间最小距离值的总和,再对总和求平均作为以随机有限集(RFS)理论为基础的目标检测与跟踪性能的评价指标。OSPA由Schuhmacher等[14]在2008年最先提出,近年来,OSPA在目标检测与跟踪领域得到了广泛应用。其定义为:

其中:X={x1,x2,…,xm},Y={y1,y2,…,yn};Πn为{1,2,…,n}上所有排列的集合;d(c):=min[(c, d(x,y)];p为用于惩罚目标状态参数的估计偏差的阶数;c为用于惩罚目标个数的估计偏差的截断参数。
3.2 仿真实验
为了验证平滑器的性能,在一个杂波环境下含有4个目标的二维目标运动场景中进行仿真实验,实验模型为一个非线性非高斯运动模型,考虑一个有不同转弯速率的匀速转弯模型以及一个具有距离和方位的量测模型。设k时刻第n(n=1、2、3、4)个目标的状态向量为xk,n=[,,,]T,其中:)为目标位置;)为目标速度。目标运动状态方程为:

其中:F为目标状态转移矩阵;vk为过程噪声且为零均值高斯白噪声,该噪声转移矩阵为G。设F、G分别为:
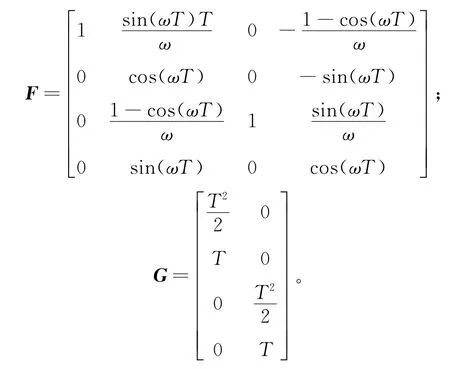
其中:ω为转弯速率;传感器采样间隔T=1 s。测量时间长度为40 s,目标的运动轨迹如图1所示。其中目标1出现于时刻1,消失于时刻7;目标2出现于时刻8,消失于时刻25;目标3出现于时刻12,消失于时刻37;目标4出现于时刻26,消失于时刻40。传感器量测模型由噪声的距离和方位量测构成,可表示为:

其中量测噪声wk为零均值高斯白噪声。目标存活概率为0.99,目标检测概率为0.9。杂波为一个服从泊松分布的随机有限集,且杂波平均数为3(m2)-1。

图1 目标真实运动轨迹Fig.1 Real target trajectories

图2 目标真实数目估计Fig.2 Estimation of real target numbers

图3 OSPA对比图Fig.3 Comparison of OSPA
3.3 算法性能分析
图2为3种滤波器对目标真实数目估计的对比。从图2可看出,GM-CPHD平滑器估计目标数目的性能优于GM-CPHD,GM-PHD最差,这是因为PHD滤波易出现高阶势分布信息丢失,从而导致对目标的估计出现偏差,当目标数目较多时,这个偏差会很大。另外,CPHD滤波结合平滑算法综合利用了t时刻前后的PHD滤波估计信息,进一步改善了平滑时对多个目标的状态估计,虽然对目标的估计有滞后现象(在开始和结尾都存在),但总体来说,GM-CPHD平滑器的检测性能仍比未经平滑处理的GM-CPHD稳定一些。
图3用OSPA度量表征3种滤波器的性能差异。当OSPA度量距离越小,表明滤波算法的精度越高,OSPA中的参数设为c=100,p=2。从图3(a)可看出,GM-CPHD平滑器优于GM-CPHD和GMPHD,这是因为CPHD充分利用了原始量测数据,可更好地对目标进行检测与跟踪。从图3(b)可看出, GM-CPHD平滑器的OSPA距离误差总和要少于GM-CPHD和GM-PHD,这是因为GM-CPHD平滑器的后向平滑递归公式改进了未经平滑处理的CPHD递归公式,并基于高斯混合方法实现,使得计算量减少。
4 结束语
GM-CPHD平滑器的实现不仅避免了传统方法中的数据关联,也提高了目标状态估计的精度。虽然滤波过程仍会出现跟踪滞后现象,但将CPHD滤波与平滑算法相结合,综合利用了t时刻前后的CPHD滤波估计信息,弥补了PHD滤波易丢失高阶势分布信息的缺点,进一步改善了多目标状态的估计性能。考虑到实现过程中计算量十分庞大,因此对CPHD平滑器进行高斯混合实现,有效地减少了计算量,并提高了跟踪性能。下一步的工作,可从以下几个方面进行研究:1)可将CPHD平滑算法基于粒子滤波方法实现,并结合TBD技术应用于低信噪比目标检测; 2)将该方法应用于交互式机动多目标模型;3)将伯努利滤波与平滑算法相结合,并基于粒子滤波或高斯混合,从而实现对机动多目标进行检测与跟踪。
[1] Mahler R.Multi-target Bayes filtering via first-order multi-target moments[J].IEEE Transactions on Aerospace&Electronic Systems,2003,39(4):1152-1178.
[2] Vo B N,Singh S,Doucet A.Sequential Monte Carlo implementation of the PHD filter for multi-target racking [C]//Proceedings of the International Conference on Information Fusion.Cairns:ISIF,2003:792-799.
[3] Vo B N,Singh S,Doucet A.Sequential Monte Carlo methods for multi-target filtering with random finite sets[J].IEEE Transactions on Aerospace&Electronic Systems,2005,41(4):1224-1245.
[4] Vo B N,Ma W.The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Signal Processing,2006,54(11):4091-4104.
[5] Mahler R.A theoryof PHD filters of higher order in target number[J].Signal Processing,Sensor Fusion,and Target Recognition XV,SPIE Defense&Security Symposium,2006:6235(K):1-12.
[6] Mahler R.PHD filters of higher order in target number [J].IEEE Transactions on Aerospace&Electronic Systems,2007,43(3):1523-1543.
[7] Erdinc O,Willett P,Bar-Shalom Y.A physical-space approach for the PHD and CPHD filters[J].Signal Processing,Sensor Fusion,and Target Recognition XV, SPIE Defense&Security Symposium,2006,6236(19): 1-11.
[8] Vo B T,Vo B N,Cantoni A.Analytic implementations of probability hypothesis density filters[J].IEEE Transactions on Signal Processing,2007:3553-3567.
[9] Nandakumaran N,Punithakumar K,Kirubarajan T.Improved multi-target tracking using probability hypothesis density smoothing[J].Proceedings of the SPIE Conference on Signal and Processing of Small Targets, 2007,6699(M):1-8.
[10] Nandakumaran N,Tharmarasa R,Lang T,et al.Gaussian mixture probability hypothesis density smoothing with multistatic sonar[J].Proceedings of the SPIE Conference on Signal Processing,Sensor Fusion and Target Recognition,2008,6968(7):1-8.
[11] Vo B N,Ma W K.A closed form solution for the probability hypothesis density filter[C]//Proceedings 8th Annual Conference on Information Fusion,Philadelphi, 2005:856-863.
[12] Mahler R,Vo B T,Vo B N.Forward backward probability hypothesis density smoothing[J].IEEE Transactions on Aerospace&Electronic Systems,2012,48 (1):707-728.
[13] Kitagawa.G.Non-Gaussian state space modelling of nonstationary time series[J].Journal of American Statistical Association,1987,82:1032-1063.
[14] Schuhmacher D,Vo B T,Vo B N.A consistent metric for performance evaluation in multi-object filtering[J]. IEEE Transactions on Signal Processing,2008,56(8): 3447-3457.
编辑:张所滨
Multi-target tracking algorithm based on cardinalized probability hypothesis density smoother
Xie Xingxiang,Cai Ruhua,Wu Sunyong,Yan Qingzhu
(School of Mathematics and Computational Science,Guilin University of Electronic Technology,Guilin 541004,China)
When multiple maneuvering targets are estimated and tracked with probability hypothesis density(PHD)filter in clutter,it is easy to lose higher order cardinality information which will result in the estimation deviation of multi-target.A multi-target tracking algorithm combined cardinalized probability hypothesis density(CPHD)filter with the smoothing algorithm is proposed.The formula of CPHD smoothing is deduced reasonably according to the prediction,update steps of CPHD and combined with the backward smoothing recursion formula.In addition,the CPHD smoother based on Gaussian mixture is also proposed.Simulation results show that the proposed solution is better than the CPHD filter without smoothing.
probability hypothesis density;cardinalized probability hypothesis density;Gaussian mixture;smoother
TN911
A
1673-808X(2015)02-0121-06
2014-12-09
国家自然科学基金(61261033,41201479,61062003,61162007);广西自然科学基金(2013GXNSFBA019270);桂林电子科技大学研究生教育创新计划(GDYCSZ201431)
蔡如华(1971-),男,广西玉林人,副教授,研究方向为小波分析在信号处理中的应用。E-mail:ruhuac@guet.edu.cn
谢兴祥,蔡如华,吴孙勇,等.基于势概率假设密度平滑器的多目标跟踪算法[J].桂林电子科技大学学报,2015,35(2):121-126.
