基于可靠度的连续相位软解调算法及仿真

杨 勇，张 凯

（西安烽火电子科技有限责任公司，陕西 西安 710075）

基于可靠度的连续相位软解调算法及仿真

杨 勇，张 凯

（西安烽火电子科技有限责任公司，陕西 西安 710075）

连续相位调制具有频谱利用率高、较低的带外功率、信号恒包络等特性，广泛地应用于无线通信系统中。然而现有的基于概率域的解调算法复杂度较高，不具有实用价值。针对这一问题对高效的相位连续调制技术进行了详细讨论，进而提出了基于可靠度的低复杂度CPM软解调算法。提出的软解调算法计算接收信号与调制信号之间的相关值，并将其作为信息度量。算法不依赖于信道噪声方差，避免了信道噪声方差估计不准确对解调性能带来的影响。仿真结果表明，提出的基于可靠度的软解调算法的性能与概率域下的解调算法几乎没有差异，并且完全能够与现代纠错码相结合，从而提高通信系统的可靠性。

连续相位调制；前向纠错码；格图；可靠度信息

0 引言

为解决日益增长的通信业务需求与频谱资源之间的矛盾，通常是在通信系统中采用高效的连续相位调制（Continuous-Phase Modulation，CPM）方式。CPM具有较高的频谱效率、较低的带外功率、信号恒包络等特性［1］，能够有效地克服频谱资源日益紧缺这一问题，将现代编译码技术与CPM调制技术相结合，不但能够提高系统的可靠性，还能够提升频谱利用率。CPM解调可分为硬解调和软解调，硬解调算法的复杂度相当低，如维特比（Viterbi）算法［2］。软解调算法（又称BCJR算法或前向后向算法）［3，4］是基于概率或对数似然比（Log Likelihood Ratio，LLR）的一种解调算法，能够与现代纠错码相结合，如低密度奇偶校验码（Low-Density Parity Check，LD-PC）码［5］，且算法复杂度远高于硬解调。

1 CPM信号与解调算法

1.1 信号表达式

CPM信号归一化功率基带复包络数学表达式为：

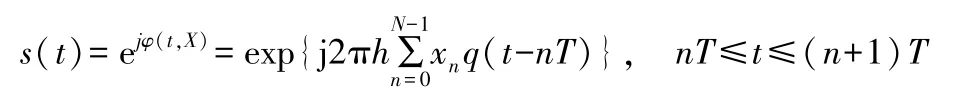
式中，T为CPM符号时长，q（t）为相位脉冲响应，q（t）＝∫＋∞－∞g（t）dt，这里函数g（t）表示频率脉冲响应，其表达式为：

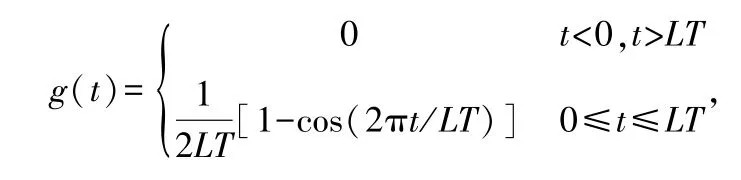
L为正整数，表示CPM信号的记忆长度。当L＝1时，CPM为全响应CPM；当L≥1时，CPM为部分响应CPM。

φ（t，X）表示携带信息的时变相位，h为调制指数，X＝｛X0，X1，…，Xn，…XN－1｝表示长度为N的信息序列，Xn，（0≤n＜N）为独立同分布的随机变量，取值集合为｛x｜x＝2（i－M）＋1，（i＝0，1，…，M－1）｝。其中，M表示CPM的进制数。令B（x）＝［b0，b1，…，blog2M－1］为与符号x相对应的整数i的二进制序列。这样符号x与B（x）之间建立了一一对应的关系，信源产生的二进制序列可以转换为对应的信息序列。

1.2 连续相位调制

为简单起见，本文仅考虑L＝1时的CPM信号。从编码的角度来看，CPM信号具有记忆效应，当前时刻的相位与本时刻和上一时刻的输入信息相关。因此可以将CPM的调制过程看作是在Trellis上的编码过程。图1给出了调制指数h＝0．5、2CPM时的Trellis。图中横坐标为时间，T为一个CPM符号的时长，纵坐标为2CPM信号起始（或终止）相位状态。

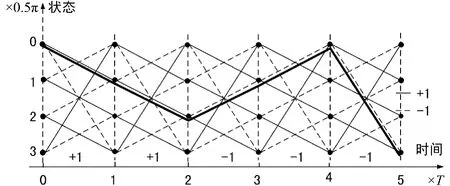
图1 2CPM、h＝0．5时的Trellis

从上述可知，CPM信号是定义在Trellis上的，因此凡是适用于卷积码［6］的译码算法都能够用于CPM解调。CPM信号在概率域下的解调算法详见文献［7］，算法中涉及了大量的指数、乘法和归一化运算，导致这类算法的复杂度非常高。为了降低复杂度，同时又避免解调性能上的损失，经过对BCJR算法中信息度量进行改进，又出现了基于对数的最大后验概率（Log Maximum a Posteriori，Log-MAP）算法、Max-Log-MAP算法［8］。为了进一步降低算法复杂度，将在下一节给出基于可靠度的CPM软解调算法。

2 基于可靠度的CPM软解调算法

2.1 信号模型

设每段CPM波形采样K点，第n个符号对应的调制信号波形为sn（t），经高斯信道后，接收端采样值为rn（k）＝sn（k）＋w（k），（k＝0，1，…，K－1）。其中，sn（k）为sn（t）的采样值，w（k）为服从均值0、方差σ2的二维高斯分布的采样值。第n（0≤n＜N）节Trellis各条边的后验概率γn（p，q）计算如下：

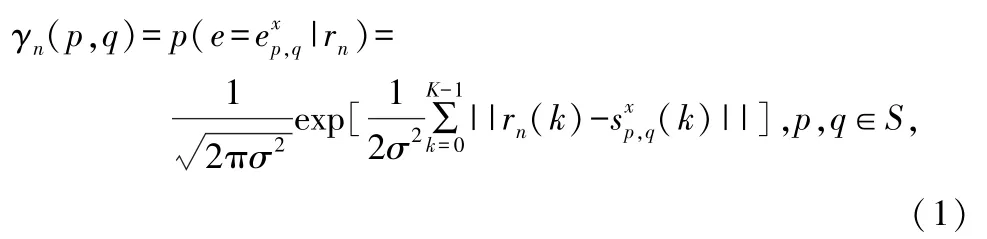
符号｜｜·｜｜表示欧氏距离。

2.2 信息度量的定义

基于可靠度的软解调算法不再以概率作为衡量符号或比特的度量，而是以概率的对数作为度量。对式（1）求对数得：

式中，I［x］、Q［x］分别表示x的实部和虚部。在一个符号周期T内，上式第一项和第二项都是与（或）独立的（任意改变（或），不影响这两项的计算结果）。考虑到对数域信息度量R［γn（p，q）］一般具有如下形式：

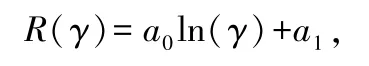
式中，a0、a1是2个与γ独立的参数。那么，对于上式，通过选择合适的a0、a1并进行线性变换后，可得到边的可靠度信息：

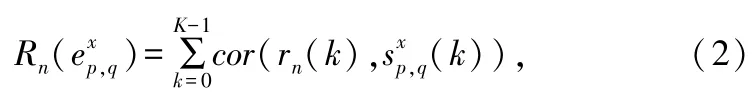
上式说明，可靠度Rn（）可以看作接收信号和发送调制信号之间的一种“相关操作”。因此，式（2）是从信号相关性角度导出的信息可靠度形式。这里需要说明的是边的可靠度信息并不能够“准确”地反映出对应边的概率大小，可靠度有可能过高估计了某些“可靠”的信息分量，所以类似于文献［9，10］，需要用修正系数ξ来降低这些过量的估计。修正后边的可靠度信息有如下形式：

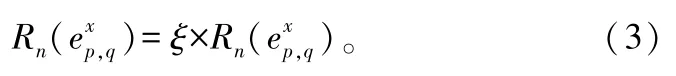
2.3 可靠度平移准则

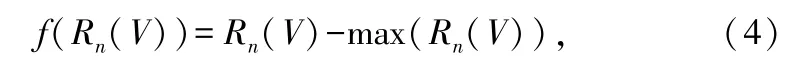
式中，符号max（X）表示向量X中的最大数值。这样，经平移后最有可能发送的波形的可靠度为0，其余波形的可靠度均不大于0，从而避免了数值正向溢出情况的发生。

2.4 算法描述

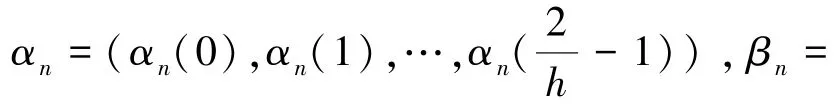
①初始化：根据式（2）、式（3）计算第n（0≤n＜N）节Trellis各条边修正后的可靠度信息

②前向递归：将前向递归变量初始化为α0＝（0，－∞，…，－∞），递归计算：

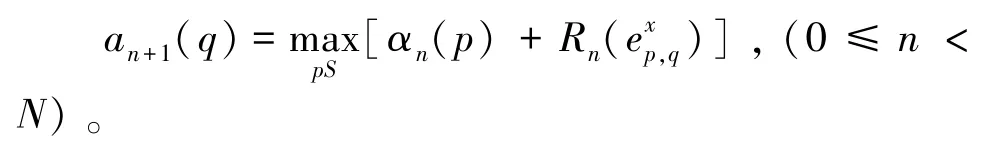
同时根据可靠度平移准则对信息向量αn＋1进行平移。

③后向递归：将后向递归变量初始化为βn＝（0，0，…，0），递归计算：

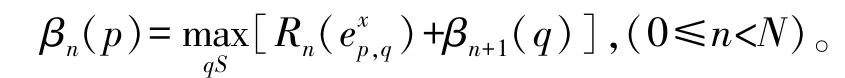
同时根据可靠度平移准则对信息向量βn进行平移。

④信息提取：关于第n个符号x的可靠度信息Rn（x）计算如下：

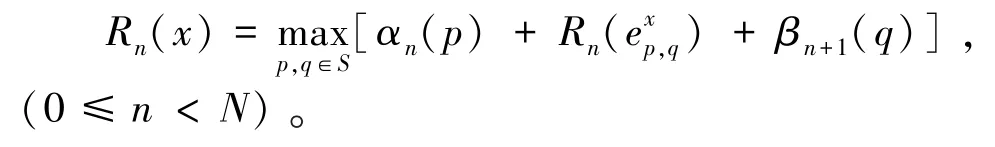
3 性能仿真

3.1 仿真1

从性能曲线中可以看到，不论CPM调制参数如何选取，基于概率域的解调算法和基于可靠度的解调算法的性能曲线基本一致，没有任何性能上的损耗，而其计算复杂度却大大降低。

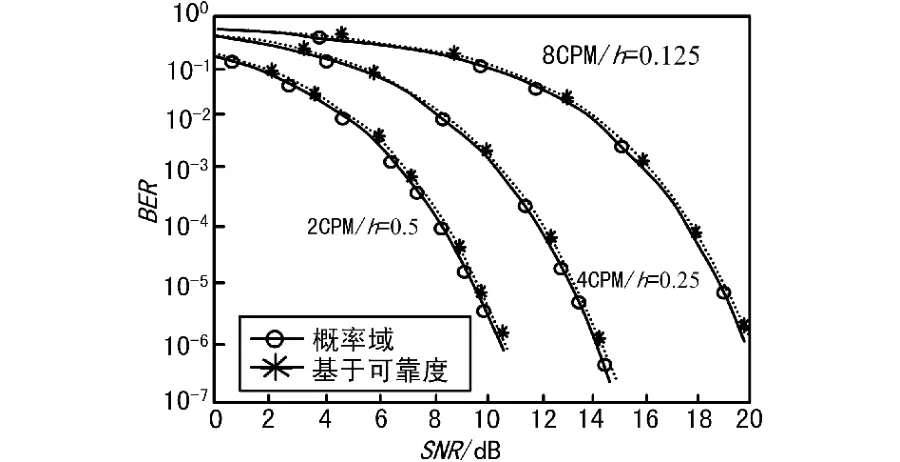
图2 不同调制参数下CPM解调性能

3.2 仿真2

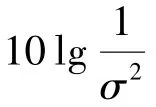
从曲线中可以看到在适当选取修正因子的情况下，以可靠度作为信息度量的解调／译码算法的性能基本与以概率作为信息度量的解调／译码算法性能相同。例如在误码率BER＝10－5时，2种算法间的差异仅有0.02 dB，几乎可以忽略。

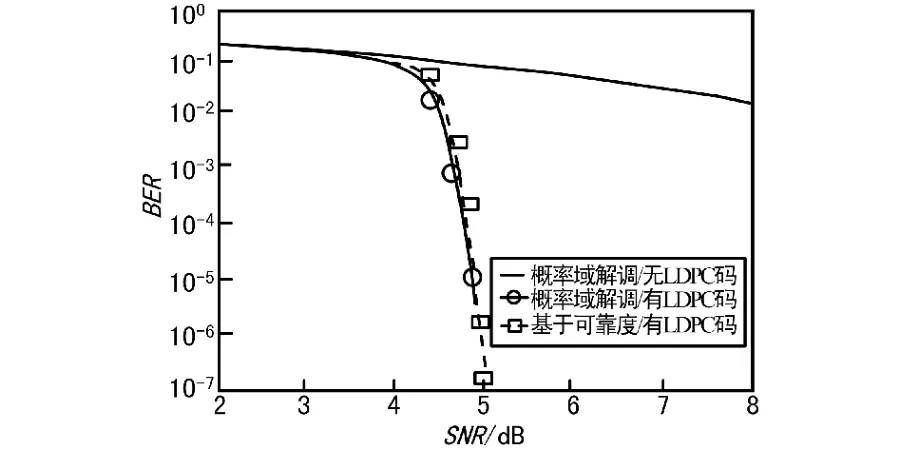
图3 4CPM／h＝0.25时结合LDPC码的性能

4 结束语

连续相位调制是一种高效的调制方式，具有频谱紧凑、恒包络等特点，能够有效地克服频谱资源日益紧缺这一问题。在详细介绍相位连续调制技术的基础上，针对传统软解调算法复杂度过高这一问题，提出了基于可靠度的低复杂度CPM软解调算法。该算法以概率的对数作为度量，其本质是接收信号和发送调制信号之间的一种“相关操作”，因此大大降低了算法复杂度。同时给出了可靠度平移准则，从而确保了在运算过程中可靠度不会溢出，为工程实现奠定了理论基础。仿真结果表明，基于可靠度的软解调算法在选取适当修正因子的情况下，其性能与概率域下的联合迭代译码算法几乎没有差异。

［1］Aulin T，Sundberg C E.Continuous Phase Modulation–parts I and II［J］.IEEE Transactions on Communications，1981，29（3）：196－225.

［2］Viterbi A J.Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm［J］.IEEE Trans.Information Theory，1967，13（1）：260－269.

［3］Bahl L R，Cocke J，Jelinek F，et al.Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate［J］.IEEE Transactions on Information Theory，1974，20（2）：284－287.

［4］Ma X，Kavˇcic A.Path Partitions and Forward－only Trellis Algorithms［J］.IEEE Transactions on Information Theory，2003，49（1）：38－52.

［5］张 凯，杨 勇.一种适用于大数逻辑可译LDPC码的自适应译码算法［J］.电讯技术，2015，55（1）：68－72.

［6］Elias P.Coding for Noisy Channels［J］.IRE Convention Record，1955，4：37－46.

［7］Ma X，Zhang K，Chen H，Bai B.Low complexity XEMS Al-gorithms for Nonbinary LDPC Codes［J］.IEEE Transactions on Communications，2012，60（1）：9－13.

［8］Robertson P，Villebrun E，Hoher P.A Comparison of Opti-mal and Sub-optimal MAP Decoding Algorithms Operating in the Log Domain［C］／／Proceedings of the Int’l Conj on Comm.（ZCC｝，Seattle，WA，1995：1009－1013.

［9］DeclercqD，Fossorier M.Decoding Algorithms for Nonbinary LDPC CodesoverGF（q）［J］.IEEE Transactions on Information Theory，2007，55（4）：633－643.

［10］Chen J，Dholakia A，Eleftheriou E，et al.Reduced-complexity Decoding of LDPC Codes［J］.IEEE Transactionson Communications，2005，53（8）：1288－1299.

［11］MacKay D J C.Good Error-correcting Codes Based on Very Sparse Matrices［J］.IEEE Transactionson Information Theory，1999，45（2）：399－431.

［12］Chen H，Zhang K，Ma X，et al.Comparisons between Reli-ability-based Iterative Min-sumand Majority-logic Decoding Algorithms for LDPC Codes［J］.IEEE Transac-tions on Communications，2010，59（7）：1766－1771.

Reliability-Based Soft Demodulating Algorithm for CPM and its Simulation Results

YANG Yong，ZHANG Kai
（Xi’an FengHuo Electronic Technology Co.，Ltd.，Xi’an Shaanxi 710075，China）

Continuous-Phase Modulation has been widely used in different communication systems due to the advantages like high spectrum utilization，low side-lobe power and constant envelope.However the probabilistic demodulating algorithm for CPM has high computational complexity and is not adaptive to practice.For this problem，the CPM technology is discussed，and further a reliability-based soft demodulating algorithm for CPM is proposed.The proposed reliability-based demodulating algorithm takes the mutual correlation between

signal and modulated signal as information metric.The algorithm is independent of variance of channel noise，which avoiding the effect of inaccurate estimate of channel.Simulation results show that，the reliability-based demodulating algorithm performs as well as the probabilistic demodulating algorithm，and can be combined with LDPC codes to improve the reliability of communication system.

Continuous-Phase Modulation；Forward-Error-Correction；trellis；reliability information.

TN76

A

1003－3114（2015）06－46－4

10.3969／j.issn.1003－3114.2015.06.12

杨 勇，张 凯.基于可靠度的连续相位软解调算法及仿真［J］.无线电通信技术，2015，41（6）：46－49.

2015－06－05

杨 勇（1977―），男，高级工程师，主要研究方向：无线通信系统设计和电台设计。张 凯（1979―），男，博士，高级工程师，主要研究方向：通信中的信号处理、信息论和信道编译码技术。