凸函数的一个性质及其几何应用
2015-06-23鞠振晓李艳丹郭洪欣
鞠振晓,李艳丹,郭洪欣
(温州大学数学与信息科学学院,浙江温州 325035)
凸函数的一个性质及其几何应用
鞠振晓,李艳丹,郭洪欣
(温州大学数学与信息科学学院,浙江温州 325035)
首先证明了凸函数的一个简单性质:次线性增长的单调增凸函数必然是常数,然后讨论了具有非负Ricci曲率的黎曼流形上热方程解的Boltzmann-Shannon熵,证明了它是单调增的凸函数,并由此给出古典解是常数的等价刻画,最后通过例子,说明了至少在非紧情形下,所给出的刻画是最优的.关键词:凸函数;次线性增长;Boltzmann-Shannon熵;古典解
1 实数集上凸函数的一个性质
凸函数是一类应用非常广泛的函数,其中一个重要的应用是证明不等式.称f( t)是区间I上的凸函数是指,对任意的a, b∈I, λ∈(0,1)都有f(λa+(1-λ)b)≤λf( a)+(1-λ)f( b).
如果f( t)在I上是一阶可导的,则f( t)是凸函数,等价于f′(t)是I上的增函数;如果f( t)在I上二阶可导,则f( t)是凸函数,等价于f′′(t)≥0.这些内容在经典的《数学分析》课程都有讲述,见文献[1].本文将考查单调增函数的一个简单性质,并用它来刻画具有非负Ricci曲率的黎曼流形上热方程的古典解.下面先给出次线性增长的定义.

在[a, b]中利用Lagrange中值定理,∃ξ∈(t, 2t ),使0≤f′(ξ)<ε.
由于f( t)在(a,+∞)为凸函数,所以f′(t)是单调递增的,对∀s∈(a, T)都有f′(s)≤f′(ξ)<ε,即0≤f′(s)<ε.由ε的任意性,可知在(a, T)上f′(s)≡0.令T→+∞,f( t)在(a,+∞)上是常数,从而命题得证.

2 流形上热方程解的熵

文献[2,3]研究了上述熵.下面分紧致和非紧情形进行讨论.在紧致流形上,由于任何连续函数都是有界,从而可积,而且紧致流形边界是空集,可以自由地进行分部积分,情况要简单些.在非紧情形下,可以通过引入一个密度函数来定义熵.
2.1 紧致流形
引理1 N的一阶和二阶导数分别为:
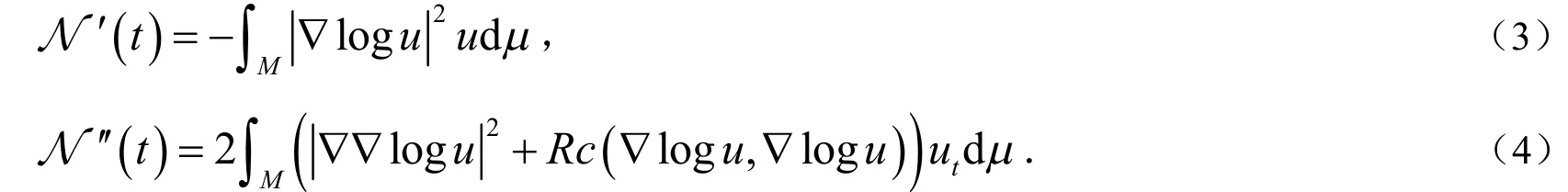
证明:本证明是直接的计算,主要的技巧是分部积分.
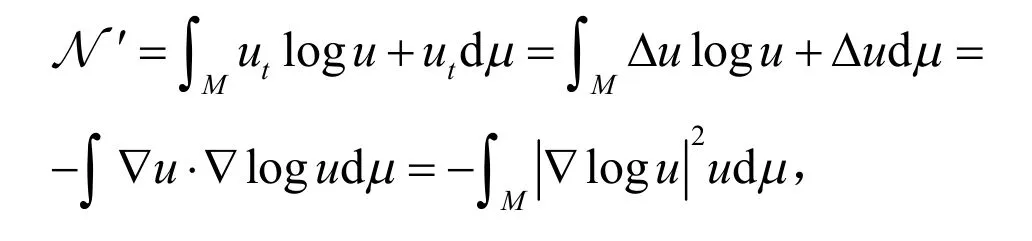

定理2 设(M, g)具有非负的Ricci曲率,则u是常数的充要条件N(-t )次线性增长.
证明:与下面定理3的证明完全相同,这里略去这个定理的证明,将证明下面的定理.
2.2 非紧流形

证明:详细的证明见参考文献[3].
定理3 设(M, g)具有非负Ricci曲率,u( x, t)为热方程的非负古典解,则u是常数的充要条件为它的熵N是次线性增长的.
证明:必要性是显然的.下证充分性.由引理1,N是单调增的凸函数,而且是次线性增长,由定理1,N是常数,它的导数是0,所以▽u=0,从而u只能是常数.
下面这个例子说明,确实有非平凡的古典解,它的熵是线性增长的.


上面例子说明,在高维空间中也确实有非平凡的古典解,它的熵是线性增长的.
[1] 华东师范大学数学系编. 数学分析[M]. 北京: 高等教育出版社, 2008: 148-154.
[2] Lim P C, Luo D J. Asymptotic estimates on the time derivative of entropy on a Riemannian manifold [J]. Advances in Geometry, 2013, 13(1): 97-115.
[3] Guo H X, Philipowski R, Thalmaier A. An entropy formula for the-dependent metric, application to ancient solutions [EB/OL]. [2013-02-02]. http://arxiv.org/abs/1305.0463.
A Property of Convex Function and Its Geometric Applications
JU Zhenxiao, LI Yandan, GUO Hongxin
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)
This paper firstly demonstrates that any increasing convex function with sub-linear growth must be a constant by means of a simple property of convex functions. Then we study the Boltzmann-Shannon entropy of positive solutions to the heat equation on Riemannian manifolds with nonnegative Ricci curvature, and prove that this entropy belongs to a monotone ncreasing convex function, and thereout turns out the fundamental solutions to be an invariable equivalent characterization. In the end, it is illustrated via examples that such an invariable equivalent characterization is optimal at least under the noncompact manifold situation.
Convex Function; Sub-linear Growth; Boltzmann-Shannon Entropy; Fundamental Solution
O186.1
A
1674-3563(2015)01-0006-05
10.3875/j.issn.1674-3563.2015.01.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2014-04-09
国家自然科学基金(11001203);浙江省自然科学基金(LY13A010009)
鞠振晓(1977- ),男,河南邓州人,硕士研究生,研究方向:微分几何
