一类包含集值映射的H-半变分不等式解的存在性

林珍香，阮志毅，钟一文

（1.福建农林大学计算机与信息学院，福建福州350002；2.海南师范大学数学与统计学院，海南海口571158）

一类包含集值映射的H-半变分不等式解的存在性

林珍香1，阮志毅2，钟一文1

（1.福建农林大学计算机与信息学院，福建福州350002；2.海南师范大学数学与统计学院，海南海口571158）

考虑一类包含集值算子的H-半变分不等式问题，应用广义的φ-α-稳定单调和著名的KKM定理证明这类问题解的存在性.

H-半变分不等式；KKM定理；Clarke方向导数

假设E为一个自反的Banach空间，E∗为其共轭空间.并且假设K为E上的一个非空、有界、闭凸子集，T：E→Lp（Ω；Rk）为一个线性连续紧算子其共轭算子为T∗：Lq（Ω；Rk）→E∗，其中1＜p＜∞，1≤k，q为p的共轭指数.若设J：Lp（Ω；Rk）→R为任一局部Lipschitz泛函，则可引入广义Clarke方向导数J°（u，v）和广义的Clarke梯度

于是，可以定义如下这样一个集合

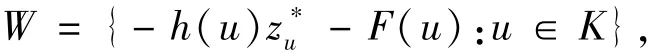
本文主要研究此类包含集值映射的H-半变分不等式问题（P），具体描述如下：（P）找到一个u∈K，以及u∗∈A（u）使得

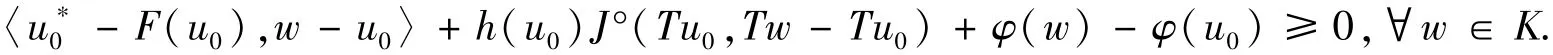
利用KKM定理将得到问题（P）解的存在性定理.

定理1设K是一个实自反Banach空间E上的一个非空、有界、闭凸子集.假设如下条件成立：

（H1）h：E→R是一个非负弱连续泛函；

（H2）F：E→E∗为一个算子并且满足如下函数是弱下半连续的：

（H3）T：E→Lp（Ω；Rk）是一个线性紧映射；

（H4）J：Lp（Ω；Rk）→R为一个局部Lipschitz泛函；

（H5）A：E→P（E∗）为下半连续并且关于集合W为φ-稳定拟单调的；

（H6）φ：E→R为一个真凸下半弱连续泛函.

那么，问题（P）至少存在一个解.

1 主要定义和引理

记P（E）为自反的Banach空间E上的所有非空子集合，同时定义集值算子A：E→P（E∗），并且记co｛u1，u2，…，un｝为｛u1，u2，…，un｝的凸包.

定义1A：E→P（E∗）是一个集值算子，两个单值函数φ：E→R和α：E→R.如果对于任意的ξ∈W以及任意的u，v∈K都满足如下的关系式：〈u∗-ξ，v-u〉+φ（v）-φ（u）＞0⇒〈v∗-ξ，v-u〉+ φ（v）-φ（u）≥α（v-u），∀u∗∈A（u），∀v∗∈A（v），称算子A关于集合W为φ-α-稳定拟单调.

定义2［1-2］设H1，H2为两个Hausdorff拓扑空间，称集值算子A：H1→P（H2）是

（1）下半连续的 （在x0）.当且仅当对于任意开集V⊂H2，满足A（x0）∩V≠∅，总存在x0的一个领域U使得对于所有的x∈U有A（x）∩V≠Ø.若称A是下半连续的，当且仅当对于每一个点x∈H1都是下半连续的.

（2）下H半连续的 （在K）.当且仅当A对于每一条限制在K上的线段都是下半连续的.

定义3［3］设K为Hausdorff拓扑空间H上的一个非空子集，A：K→P（H）为一集值算子.称A为一个KKM映射，如果对于任意的｛u1，u2，…，un｝⊂K，总有co｛u1，u2，…，un｝⊂∪A（uj）.

引理1［4］设J：K→R是u∈K上的一局部Lipschitz函数，那么有

（1）函数v→J°（u，v）为有限值并且满足正其次性和次可加性；

（2）函数J°（u，v）关于变量（u，v）为一个上半连续函数.

引理2［5］设H1，H2为两个Hausdorff拓扑空间，A：H1→P（H2）为一个集值算子.则A为下半连续算子，当且仅当对于任意（x，y）属于A的图像以及任意一个收敛到x的网｛xλ｝λ∈I⊂H1，可以得到对于任意的λ∈I，存在yλ∈A（xλ）使得yλ→y.

引理3［3］设K为Hausdorff拓扑空间H上的一个非空子集，假设G：K→P（E）为一集值算子并且满足如下性质

（1）G为一个KKM映射；

（2）对于每一个x∈K，集合G（x）为一个闭集；

（3）存在一个x0∈K，使得集合G（x0）为一紧集.那么∩x∈KG（x）≠Ø.

2 定理1的证明

首先定义如下这样一个集值映射G：K→P（K）：

对于集值映射G，考虑如下两种情况：（1）G不是一个KKM映射；（2）G是一个KKM映射.

2.1 G不是一个KKM映射

那么将存在一个u0的领域U使得所有的v∈U∩K和i∈｛1，2，…，n｝满足

假设上述不成立，那么对于u0的任意领域U，则存在v0∈U∩K和i0∈｛1，2，…，n｝使得

这与假设G不是一个KKM映射矛盾.于是可知对于所有的v∈U∩K有

由于，集值算子A关于集合W是φ-稳定拟单调的，那么对于任意的j∈｛1，2，…，n｝，

等价于

利用Clarke广义方向导数J°（u，v）的次可加性，可以得到

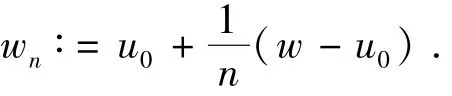
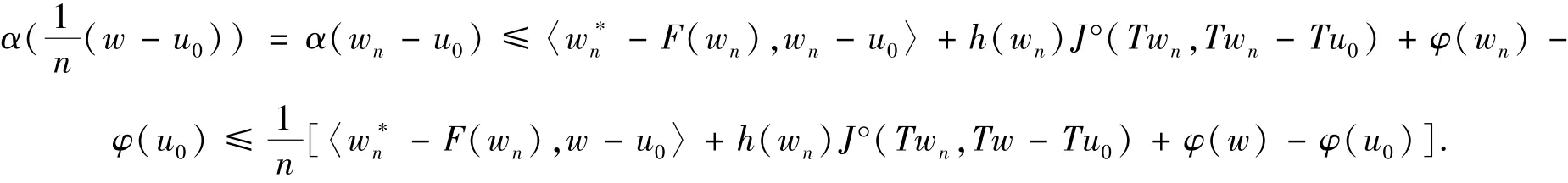
2.2 G是一个KKM映射

若G是一个KKM映射，那么对于任意的v∈K，下面来证明集合G（v）为一个弱闭集.对于任意的序列｛un｝⊂G（v）满足un在E上弱收敛到u.利用函数T为线性紧算的、h是弱连续、φ是弱下半连续、Clarke广义方向导数J°（u，v）是上半连续的以及F的假设条件，可以得到对于每个v∗∈A（v）

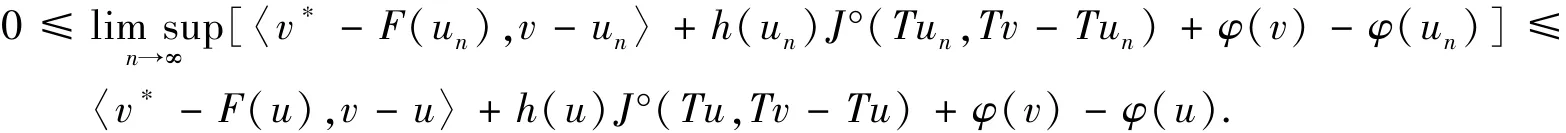
因此，集合G（v）为一个弱闭集.另一方面，由于K在自反的Banach空间E上为一个有界、闭凸子集，则K为弱紧的.那么，对于每一个v∈K，集合G（v）为一个弱紧集.因此，利用在弱拓扑下的KKM定理，可以得到∩v∈KG（v）≠∅.若u0∈∩v∈KG（v）⊂K，则对于任意的v∈K，下述不等式成立.

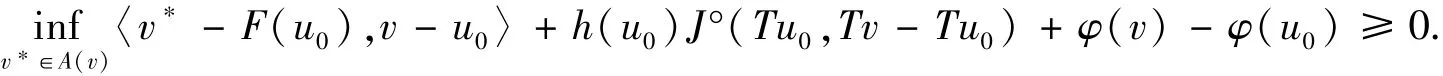
上式都成立.因此，u0∈K为问题 （P）的一个解.

［1］COSTEA N，ION DA，LUPU C.Variational-like inequality problems involving set-valued maps and generalized monotonicity［J］.Optim Theory Appl，2012，155：79-99.

［2］PANAGIOTOPOULOS P D.Hemivariational inequality，applications in mechanics and engineering［M］.Berlin：Spring，1993.

［3］FAN K.Some properties of convex sets related to fixed point theorems［J］.Math Ann，1984，266：519-537.

［4］CLARKE F H.Optimization and nonsmooth analysis［M］.New York：Wiley，1983.

［5］NANIEWICZ Z，PANAGIOTOPOULOS P D.Mathematical theory of hemivariational inequalities and applications［M］. New York：Marcel Dekker，1995.

Existence of Solutions to a Class of Hemivariational Inequality Problems Involving Set-valued Operator

LIN Zhen-xiang1，RUAN Zhi-yi2，ZHONG Yi-wen1
（1.College of Computer and Information Science，Fujian Agriculture and Forestry University，Fuzhou 350002，China；2.College of Mathematics&Statistics，Hainan Normal University，Haikou 571158，China）

In this paper we considered a class of hemivariational inequality problems involving set-valued operator and applied the generalized φ-α-stable monotone and well-known KKM theorem to verify the existence of solutions for Hemivariational inequality problems.

Hemivariational inequality；KKM theorem；Clarke directional derivative

O178

A

1673-4432（2015）03-0108-04

（责任编辑 晓 军）

2014-12-17

2015-05-28

福建省自然科学基金项目 （2013J01216）

林珍香（1990-），女，硕士研究生，研究方向为不等式与计算机智能.通讯作者：钟一文 （1968-），男，教授，博士，研究方向为不等式与计算机智能.E-mail：ywzhong@fafu.edu.cn