非线性分数阶Volterra积分-微分方程的SCW数值方法

朱 莉

（厦门理工学院应用数学学院，福建厦门361024）

非线性分数阶Volterra积分-微分方程的SCW数值方法

朱 莉

（厦门理工学院应用数学学院，福建厦门361024）

推导第二类Chebyshev小波 （SCW）分数阶算子矩阵，利用SCW算子矩阵方法求解了一类非线性分数阶Volterra积分-微分方程.此方法将分数阶积分-微分方程转化成非线性代数方程组求解，可以简化分数阶方程的求解，所得到的数值结果表明该方法是有效和精确的.

分数阶微积分；SCW；Volterra积分-微分方程；算子矩阵；Block Pulse函数

近年来，分数阶微分方程的应用引起了不同领域学者的高度重视［1-3］.然而，由于分数阶微分是拟微分算子，它的保记忆性在对现实问题进行优美刻画的同时，也给分析和计算造成了很大困难，所以发展分数阶微分方程数值解法是一个迫切需要解决的问题.与其他方法相比，小波数值方法的优点是：1）离散后得到的代数方程组的系数矩阵是稀疏的；2）求解高阶方程问题只导致离散后代数方程组的维数增加；3）方程的解具有收敛性.本文主要利用第二类Chebyshev小波 （SCW）算子矩阵方法求解非线性分数阶Volterra积分-微分方程：

其中y（i）（t）表示y（t）的i阶导数；i是常数；f∈L2［0，1），k∈L2（［0，1））2是已知函数；y（x）是未知函数；Dα（r-1＜α≤r）是Caputo意义下的分数阶导数；F（y（x））是y（x）的多项式函数.为简便起见，令F（y（x））=［y（x）］q，q＞1是正整数，并假设函数f和k足够光滑.

1 基础知识

1.1 分数阶微积分［4-6］

定义1称实函数f（t），t＞0，属于空间Cυ，υ∈R，如果存在实数k（k＞υ），使得f（t）= tkf1（t），其中f1（t）∈C［0，∞），称f（t），t＞0，属于空间当且仅当∈Cυ，m∈N.

定义2函数f∈Cυ，υ≥-1的α阶Rieman-Liouville分数阶积分算子定义为：

其α（α≥0）阶分数阶导数为：

定义3函数f（t）的Caputo意义下的分数阶导数定义为：

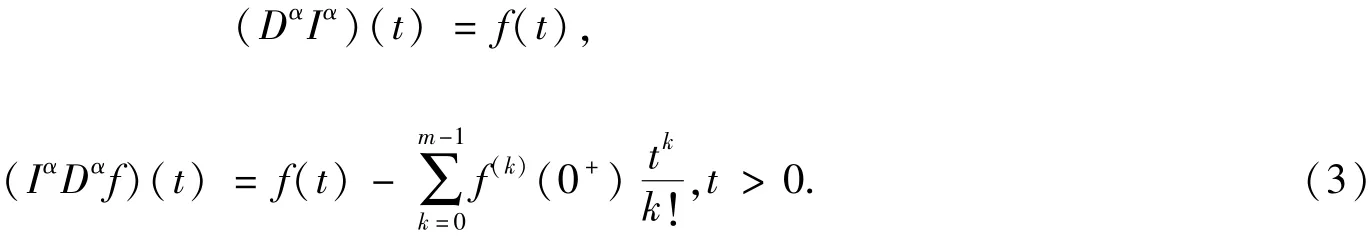
1.2 SCW的构造及函数逼近

定义在区间［0，1）上的SCW［7］满足：其中n=1，…，2k-1和k是任意正整数，且

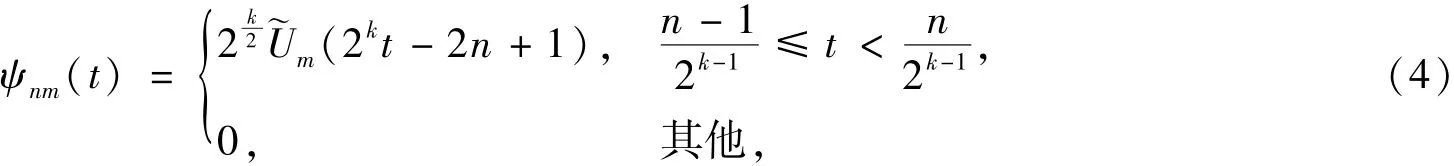
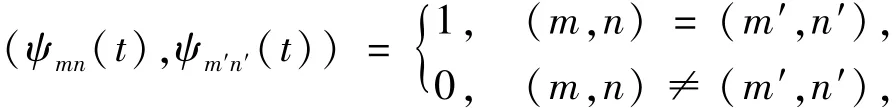
定义在［0，1］区间上的平方可积函数f（t）可以用SCW展开成如下形式：

其中系数

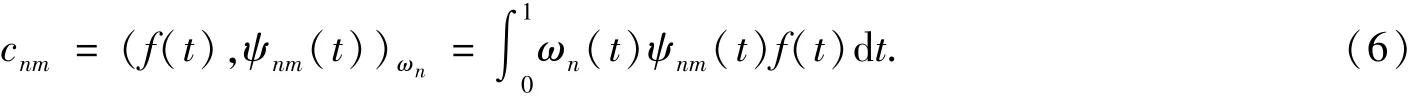
对式 （5）截断有限项，可表示为

其中系数向量C和SCW函数向量Ψ（t）形式为：

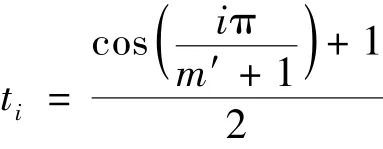
1.3 分数阶积分的算子矩阵

首先给出Block Pulse函数 （BPFs）的定义.定义在区间［0，1）的BPFs为：

其中i=0，1，2，…，m-1.BPFs具有共轭性和正交性：

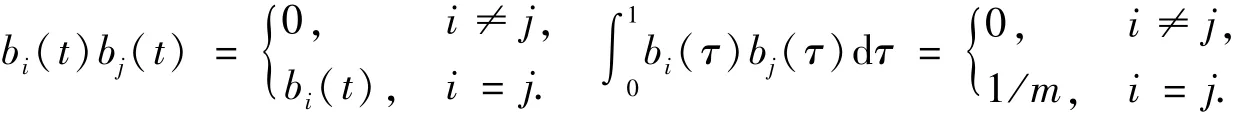
定义在［0，1］区间上的平方可积函数f（t）可以展开成如下BPFs级数的形式：

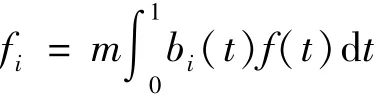
式 （11）表明SCW也可以用BPFs展开成m′项级数：

文献 ［8］给出了Block Pulse分数阶算子矩阵Fα：

其中

并且ξk=（k+1）α+1-2kα+1+（k-1）α+1.令

由式 （13）和 （14）可以得到：

2 分数阶积分算子矩阵的应用

考虑非线性分数阶Volterra积分微分方程：

函数Dαy（x）和f（x），k（x，t）均可以用SCW近似表示为：

利用式 （3），（16）和 （20），可以得到：

将式 （19）带入上式，并用SCW逼近，可以得到：

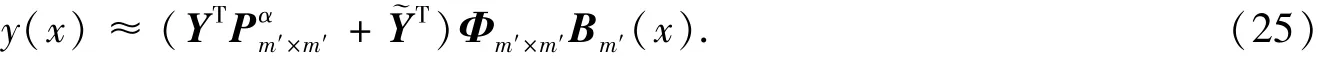
定义

等式 （25）变为

利用BPFs的共轭性，有

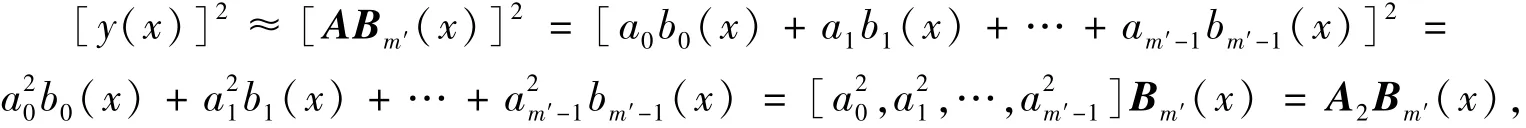
更一般的，有

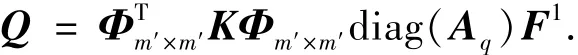
将式 （13）带入式 （20），（21），然后将所得结果和式 （28）带入式 （18），得到

对式 （29）两边同乘以Bm′（x），并在区间［0，1］积分，根据BPFs的正交性得到

式 （30）是一个非线性的代数方程组.通过求解此方程组，可以根据式 （23）得到式 （18）的近似解.

3 数值算例

利用本文的方法求解两个分数阶微分方程.为了在例1和例2中比较SCW和CAS小波方法，采用与文献 ［9］相同的误差定义，即

其中y（x）表示精确解，ym′（x）表示近似解.在数值算例中，给出当k增大时，数值解的误差情况.可以看到，当M固定时，k越大，方程的近似解越精确.所以k的最优取值由预先给定的精度来确定.

例1考虑非线性分数阶Volterra积分微分方程：

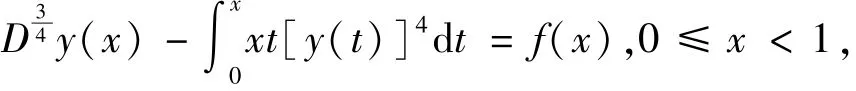
例2考虑方程：

表1给出了当α=2时，由SCW和CAS（见文献 ［9］）两种小波方法得到的例1和例2的误差.通过比较两种小波方法，发现在求解相同方程时SCW方法可以得到更高的精确度.

图1 参数k取不同值时例1的数值结果Fig.1 NumericaI resuIts for varied vaIues of k

图2 当α=1.25，1.5，1.75，2时例2的数值结果Fig.2 ApproximaIe soIution of exampIe 2 forα=1.25，1.5，1.75，2

表1 当SCW小波的参数k取不同值时的误差，以及当CAS小波的参数k=4，5时的误差［9］TabIe 1 Approximate norm-2 of absoIute errors for some k of the SCW，and for k=4，5 of the CAS waveIet［9］

4 结论

本文中引入了SCW，并推导了SCW的分数阶积分算子矩阵.利用积分算子矩阵给出了求解一类非线性分数阶Volterra积分-微分方程的数值方法.通过数值算例，将所得到的数值结果与方程的精确解和由CAS小波得到的数值结果进行了比较，从而表明SCW方法是有效的，而且具有更高的精度.

［1］MACHADO J T，KIRYAKOVA V，MAINARDI F.Recent history of fractional calculus［J］.Commun Nonlinear Sci Numer Simul，2011，16（3）：1 140-1 153.

［2］ROSSIKHIN Y A，SHITIKOVA M V.Application of fractional calculus for dynamic problems of solid mechanics：novel trends and recent result［J］.Appl Mech Rev，2010，63：52.

［3］DIETHELM K.The analysis of fractional differential equations［M］.Berlin：Springer-Verlag，2010.

［4］KACZOREK T.Selected problems of fractional systems theory［M］.Berlin：Springer-Verlag，2011.

［5］WEST B J，BOLOGNAB M，GRIGOLINI P.Physics of fractal operators［M］.New York：Springer，2003.

［6］CAPUTO M.Linear models of dissipation whose Q is almost frequency independent-II［J］.J Roy Austral Soc，1967，13：529-539.

［7］ZHU L，FAN Q B.Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet［J］.Commun Nonlinear Sci Numer Simulat，2012，17（6）：2 333-2 341.

［8］KILLICMAN A，ALZHOURZ A A.Kronecker operational matrices for fractional calculus and some applications［J］. Appl Math Comput，2007，187：250-265.

［9］SAEEDI H，MOHSENI M M.Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS wavelets［J］.Commun Nonlinear Sci Numer Simulat，2011，16：1 216-1 226.

Numerical Solution of Nonlinear Fractional-Order Volterra Integro-Diferential Equations by SCW

ZHU Li
（School of Applied Mathematics，Xiamen University of Technology，Xiamen 361024，China）

In this paper，we first derived the second Chebyshev wavelet（SCW）operational matrix of fractional integration.Then based on its results we proposed the SCW operational matrix method to solve a kind of nonlinear fractional-order Volterra integro-differential equations.The main characteristic of this approach is that it reduces the integro-differential equations into a nonlinear system of algebraic equations that simplifies solution to the problem of fractional order equation.The obtained numerical results indicate that the proposed method is efficient and accurate for equations of this kind.

fractional calculus；SCW；Volterra integro-differential equations；operational matrix；Block Pulse functions

O242.2

A

1673-4432（2015）03-0096-06

（责任编辑 晓 军）

2014-07-07

2014-11-13

厦门理工学院高层次人才项目 （YKJ12029R）

朱莉 （1984-），女，讲师，博士，研究方向为微分方程数值解.E-mail：zhulwhu@163.com