一类非自治捕食系统的动力学研究

陈新一

(西北民族大学中国民族信息技术研究院,甘肃兰州730030)

一类非自治捕食系统的动力学研究

陈新一

(西北民族大学中国民族信息技术研究院,甘肃兰州730030)

文章研究了一类更广泛的非自治捕食系统的动力学行为. 利用比较原理及构造适当的Lyapunov函数的方法得到了保证此系统持久性和全局渐近稳定性的充分条件,通过Brouwer不动点定理及伴随系统作Lyapunov函数的方法得到了正周期解和正概周期解的存在性和惟一性，也推广了已有的结果.

非自治捕食系统; 持久性; 全局渐近稳定性; 周期; 概周期

0 引言

物种的多样性,会使捕食系统中物种之间的关系相对复杂[1～3].文献[4]讨论一类非自治捕食—两共存食饵模型的动力学行为.模型为：

我们在后续的讨论中发现,上述模型中功能反应函数中x1(t)和x2(t)的指数是无关的.因此本文讨论由文献[4]模型推广得到的一类更为广泛的非自治捕食-两共存食饵模型的动力学行为.模型如下：

(1)

其中xi(t)(i=1,2,3)表示t时刻的种群密度；p≥0,q≥0是整数;系数ai(t),bi(t),ci(t),di(t),ei(t),gi(t),Di(t)(i=1,2),f(t),a3(t),t∈[0，+∞)都是连续有界严格正的函数.

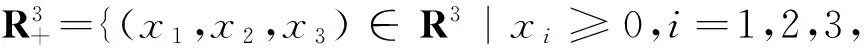
xi(t0)>0,t0≥0,i=1,2,3.

(2)

本文中我们讨论系统的持久性和全局渐近稳定性[5], 并讨论周期和概周期意义下,周期解和概周期解的存在惟一性和全局吸引性的充分条件[6].

1 一致持久性和全局渐近稳定性

(3)

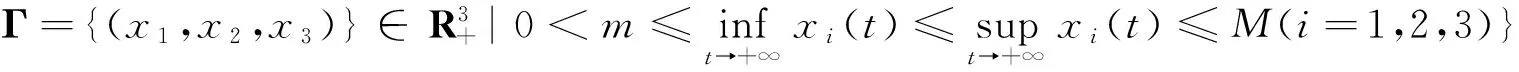
定理1 若系统(1)满足文献[4]引理3的条件,则系统(1)是一致持久的.

定理2 若系统(1)满足文献[4]引理3的条件,且下面的条件也成立.

则系统(1)的满足初始条件(2)的解(x1(t),x2(t),x3(t))是全局渐近稳定的.

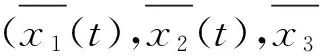
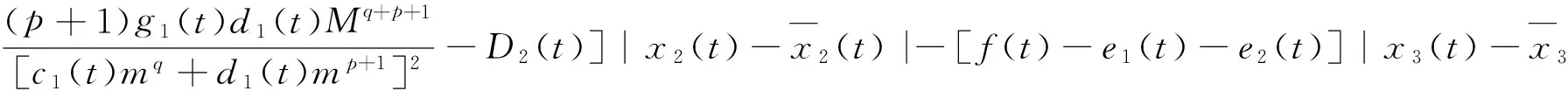
由定理的条件可知，存在η>0，使得

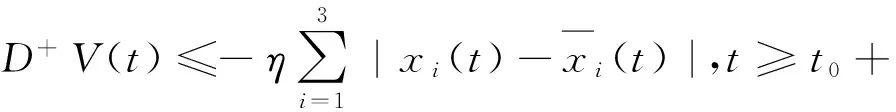
定理证毕.

例 应用定理2可以判定系统

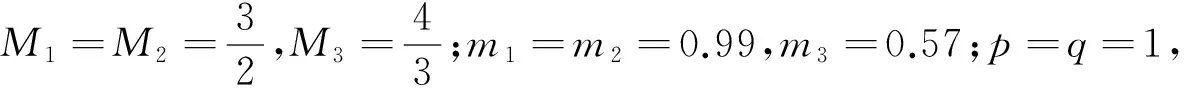
2 正周期解的存在惟一性和全局吸引性

研究种群在周期环境(如季节交替、食物供给及物种繁殖等等)中的一个最基本、最重要的问题是周期解的存在性与稳定性.如果系统(1)为一个ω的周期系统.与文献[4]相仿可得相关结论.

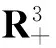
3 正概周期解的存在惟一性和全局吸引性

假设系统(1)是一个概周期系统,考虑此时这个系统的正概周期解的存在性、惟一性和全局吸引性.

定理4 如果概周期系统(1)满足文献[4]中引理3 及定理2的条件,则系统(1)存在惟一的正概周期解,且此解是大范围一致渐近稳定的.

证明 由引理2和引理3知Γ为系统(1)的最终有界区域.考虑系统(1)及其伴随系统

令xi(t)=exp{xi(t)},ui(t)=exp{ui(t)},则系统(5)可以写成

再求V(t)沿(6)解的上右导数得

D+V(t)=sgn[exp{x1(t)}-exp{u1(t)}]{-b1(t)[exp{x1(t)}-exp{u1(t)}]-e1(t)[exp{x1(t)}-

sgn[exp{x2(t)}-exp{u2(t)}]{-b2(t)[exp{x2(t)}-exp{u2(t)}]-e2(t)[exp{x2(t)}-

sgn[exp{x3(t)}-exp{u3(t)}]{-f(t)[exp{x3(t)}-exp{u3(t)}]+D1(t)[exp{x1(t)}-exp{u1(t)}]+

D2(t)]|exp{x2(t)}-exp{u2(t)}|-[f(t)-e1(t)-e2(t)]|exp{x3(t)}-exp{u3(t)}|. (7)

由中值定理得

exp{xi(t)}-exp{ui(t)}=exp{ξi(t)}{xi(t)-ui(t)},

其中exp{ξi(t)}位于exp{xi(t)}与exp{ui(t)}之间，于是由(7)可以得到

D+V(t)≤-ηV(t).

其中η可取定理2中三个数的最小者.所以由文献[7]的引理5知系统(1)存在惟一全局渐近稳定的正概周期解.

注 当p=q时,系统(1)即为文献[5]的系统(1),从而立即得到文献[5]的结果.当p=q=0,gi(t)=1(i=1,2)时,系统(1)即是文献[7]的系统(1.1),文献[7]所讨论的模型更是本文模型(1)的特例.

[1] 陈兰荪, 陈健.非线性生物动力系统[M].北京:科学出版社,1993. 54-90.

[2] 柏灵, 王克.一类具有比率型功能反应的食物链系统周期解的存在性[J].东北师范大学学报(自然科学版),2003,35(1): 1-9.

[3] 王克.具无限时滞的非自治捕食者-食饵系统的持久性[J].数学学报,1997,40(3): 321-332.

[4] 陈新一. 一类非自治捕食系统的动力学行为[J]. 山东大学学报(理学版), 2013,48(12):18-23.

[5] 秦元勋, 王慕秋,王联. 运动稳定性理论与应用[M].北京:科学出版社, 1981.23-105.

[6] 何崇佑. 概周期微分方程[M].北京:高等教育出版社,1992. 70-125.

[7] 王静, 王克. 非自治一捕食者-两互惠食饵模型的动力学行为[J]. 东北师范大学学报(自然科学版)，2005,37(1):1-6.

2015-01-20

陈新一(1957—)，男，教授，主要从事微分方程方面的研究.

O175.7

A

1009-2102(2015)02-0008-04