基于混合算法的色彩信号多光谱表示空间研究
2015-06-23孔令罔
李 梅,孔令罔
(1. 运城学院 机电工程系,山西 运城 044000;2. 武汉大学 印刷与包装系,武汉 430079)
基于混合算法的色彩信号多光谱表示空间研究
李 梅1,孔令罔2
(1. 运城学院 机电工程系,山西 运城 044000;2. 武汉大学 印刷与包装系,武汉 430079)
根据光谱光效率函数,利用聚类分析法对多光谱数据集进行线性降维,进而利用快速独立成分分析法对初次降维数据提取独立成分,然后根据独立成分进行光谱空间重建,最后从均方误差以及色度空间两方面对此方法与主成分分析法进行对比。实验结果表明,该方法的均方差平均值较PCA降低了3.64%,平均色差较PCA降低了24.08%。可见,利用混合算法重建的多光谱表示空间能够更高效地表示原始光谱空间。
多光谱空间;聚类分析;独立成分分析;均方误差;色差
0. 引言
传统的色彩复制基于同色异谱复制原理,此种复制方法受光源及周围环境的影响,不能保证色彩的始终一致性。随着社会的发展,基于多光谱重现的色彩显示与复制正在逐步走进人们的生活。但是由于多光谱数据采集的波段多,相关性强,导致存储空间大,并在进行图像颜色处理时,消耗时间长[1]。因此,快速实现数据有效提取,高效率实现颜色高精度复制已成为亟待解决的问题。本文提出以聚类分析和快速独立成分分析相结合的混合算法来实现色彩信号多光谱空间的降维与重建,并从均方误差和色度空间两方面对此方法与主成分分析法进行对比。
1. 相关原理
1.1 聚类分析
在实际应用中,单独应用聚类分析就可以根据数据的特征获得数据的分布状况,为研究者观察每一类数据的特征,进一步集中对特定的类分析带来很大的便利。所谓聚类分析就是根据一定的标准,将原始数据进行有规律的分类。目前聚类分析大体上分为层次聚类法和非层次聚类法。本文主要利用层次聚类法中的最短距离法和非层次聚类法中的K-均值法[2]。
首先在需要处理的数据中,随机选取k个值作为初始聚类点,为以后的聚类奠定基础。然后根据最短距离法对整体数据与k个值进行具体归类。这次的聚类要求所有数据都归于以k个值为中心点的类。归类完成后,求取各个类的平均值,并以该值为中心点,继续对整体数据运用最短距离法进行归类。依次类推,直到k个中心点不变为止。具体流程如图1所示。

图1 K-均值法流程图
1.2 快速独立成分分析
FICA算法[3]是实现信号盲源分离的一种方法,在实现过程中考虑了高阶的相关性[4],是寻找非高斯性最大值的不动点迭代法。该算法运用近似牛顿迭代法寻找混合信号中的独立成分,其计算量是一般梯度算法的1/20-1/50[5],收敛速度较快。
假设一组随机变量x=(x1(t),x2(t),…,xn(t))T,t是样本标号,是由独立成分s=(s1(t),s2(t),…,sn(t))T线型混合的,则混合信号可表示为式1。
x=As
(1)
式中,只有x是已知的,需要根据x来求解出s,这个过程就称为盲信号分离。当源信号数目等于混合信号数目时,解混矩阵等于混合矩阵的逆,表示为式2。
W=A-1
(2)
从而,独立成分可以由式3估算出:
s=Wx
(3)
本文中的FICA算法主要包含预处理和并行正交化算法两个方面。
1.2.1 预处理
预处理可以在一定程度上降低盲源分离问题的复杂度,有效减少工作量,所以在实现FICA算法时,通常需要对输入的原始数据进行预处理[6]。实施过程如下:
1) 中心化
对混合信号x进行中心化是一个必要条件。具体中心化方式就是用混合信号将每一列的平均值减去,使混合信号变为零均值变量。这也意味着分离出来的独立信号也是零均值的。如式4。
x-E{x}→x
(4)
2)白化
白化处理,又可称为球化处理。因为混合信号之间大都具有相关性,所以在数据处理过程中会引起收敛不稳定。因此一般情况下,都需要对混合信号进行白化或球化处理。白化处理不仅可以去除各混合信号之间的相关性,提高收敛稳定性,而且还可以简化计算过程。当混合信号的个数大于独立成分的个数时,可以实施白化直接将混合信号的维数降到与独立成分的维数相同[7]。白化原理如下:(1)根据零均值向量,计算x的协方差矩阵C;(2)计算协方差矩阵的特征值和其对应的特征向量β,如式5;(3)根据特征值及特征向量,计算白化矩阵V,如式6,其中Λ为特征值的对角阵,U为特征向量矩阵;(4)最终得到白化向量Z,如式7。
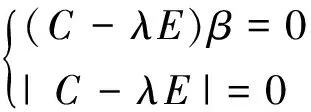
(5)
V=Λ-1/2UT
(6)
Z=Vx
(7)
1.2.2 并行正交化算法
快速ICA学习规则本质上是要找一个方向,这个方向可以使WTX的非高斯性最大。为了使计算简单,对于非高斯性度量,WTX负熵的最大近似值通常都在E{G(WTX)}的极值点处获得。即根据拉格朗日条件,在E{G(WTX)}=‖W‖2=1的约束条件下,E{G(WTX)}的最大近似值能够由式8获得
F=E{xg(WTX)}+βW=0
(8)
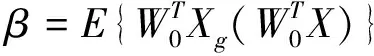
(9)
从而求得权向量W。可见,并行正交化算法进行的是并行批量迭代,是实现FICA的主要部分,所得到的结果误差较小。
最后根据权向量W得到解混矩阵提取独立成分。如式10,
S=WTZ
(10)
最终FICA具体实现流程如图2:

图2 FICA算法流程图
2. 算法实现
研究采用芬兰Kuopio大学的Munsell Color Matt光谱数据集,这个数据集包含有1269个色样的光谱反射率。这个光谱数据集是由Perkin-Elmer Lambda分光光度计在光源为D65,视场为2°的条件下,从400nm到700nm间隔5nm测量的,其中在波长400nm-420nm处,光谱反射率噪声比较大。
1)运用聚类法对原光谱集孟塞尔色卡的1269个色块的光谱反射率进行分类,达到分出来的每一组反射光谱的波形,既能达到几何上的相似分布的分布归并,也可以达到人眼视觉阈限的分布归类。然后在峰值一类的反射光谱中,选取峰值居中的反射光谱作为基准,根据光谱光效率函数[8]分别对应计算各个组中反射光谱在各个波长点处的光谱反射率之差,如果在光谱光效率函数范围内,则归为一类;反之,如果超出光谱光效率函数范围,则将其归为新的一类。聚类分析后,色样由1269组反射光谱线为972组,然后将每一类中作为基准的光谱反射率作为下面实现ICA降维的原始数据X。
2)运用快速独立成分分析法提取降维后数据的独立成分。
首先进行预处理,然后选取独立成分个数5,进而根据上述并行正交化算法求取权向量,最终实现独立成分提取s。
3)色彩信号的多光谱空间重建
色彩信号的多光谱空间是否成功重建是检验混合算法是否成功的一个关键因素。由FICA原理可知,得到混合矩阵和独立成分就可以重建多光谱空间。由上文可知,已经提取出独立成分S。而混合矩阵A可根据式6、式9推出,表示为式11:
A=V-1W-1
(11)

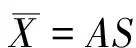
(12)
3. 结果
3.1 均方差分析
平均平方误差,顾名思义,是指估计值与真值之差平方的平均值,是光谱分布向量意义上的评价标准。公式如式13。
(13)

图3 色样的均方误差分布图
平均平方误差的值越小,说明所得实验数据与源数据相比精确度越高。整个光谱集的重建光谱与原始光谱的均方误差分布如下:
从图3中可以得知均方误差分布比较均匀,除了一个色样外,其他均在3.0 x10-4以下。混合算法与PCA[9]算法重建光谱与原光谱的均方差比较如表1。
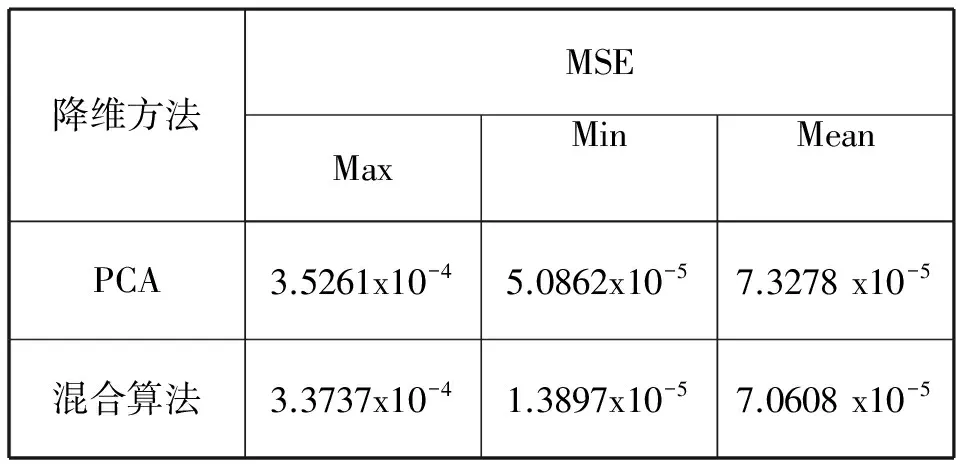
表1 混合算法降维法与PCA降维法的光谱重建均方差比较
由表1可知,经混合算法降维处理后重建的光谱误差较PCA算法的要小。MSE最大值和最小值所对应的色样的序号为1058和539。图4为具有MSE最大值及最小值的重建光谱分布和所对应的原始光谱分布。

图4 具有MSE最小值及最大值的重建和原始光谱分布
3.2 色差分析
色差是将人眼的视觉考虑在内的,属于感观评价,是色彩复制的评价标准[9]。经过该混合算法的降维,可得重构光谱与原光谱的色差如图5。
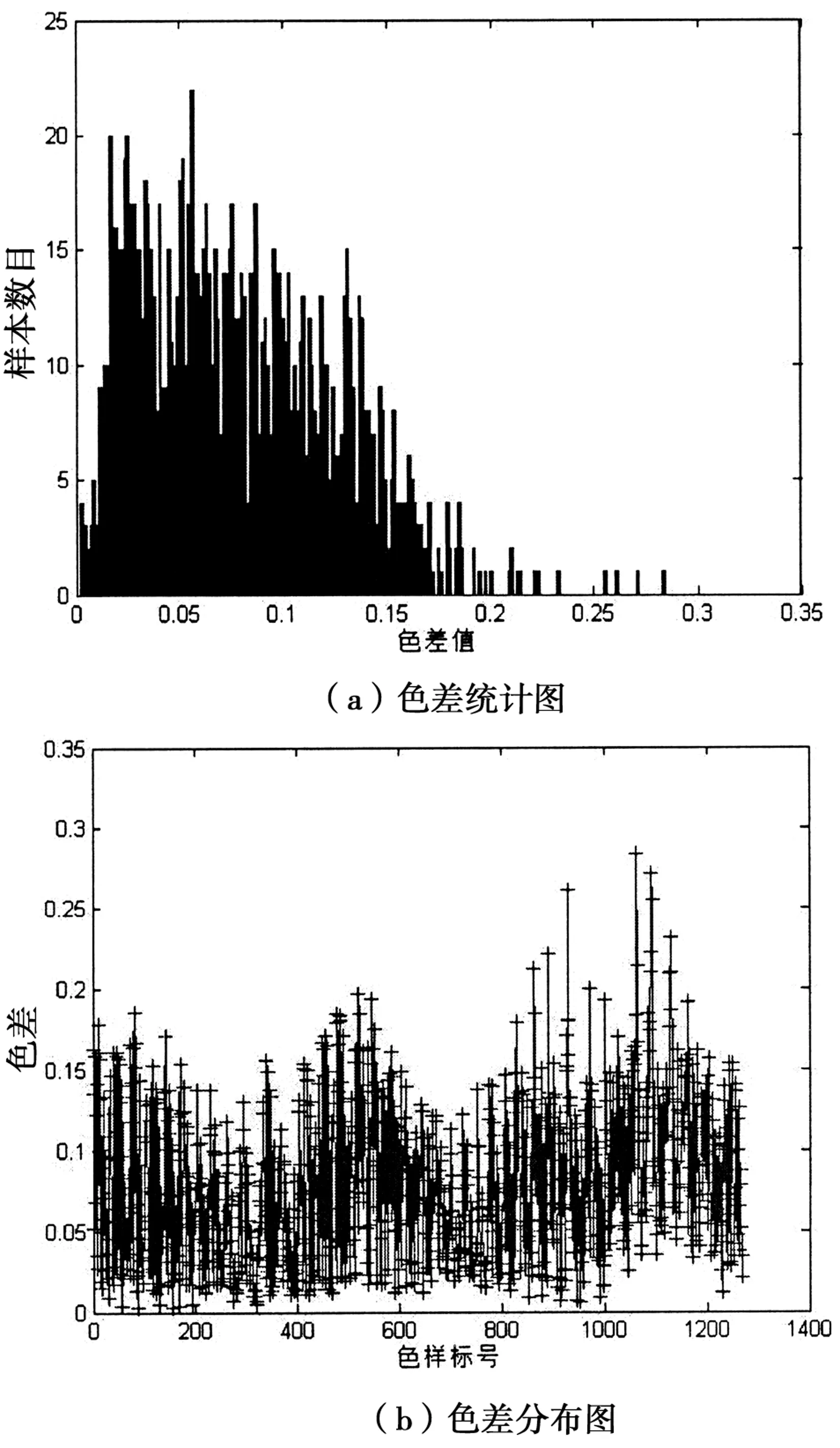
图5 色样的色差分布图
结合图5可知,混合算法重构的光谱与原光谱的色差均小于0.3,说明重构光谱表色只有微量变化,人眼感觉不到[8]。混合算法与PCA算法重建光谱与原光谱的色差比较如表2。

表2 混合算法与PCA算法重建光谱色差比较
由表2可知,两种算法重建的光谱空间表色能力都比较理想,但是经混合算法重建的光谱空间表色能力更强。
色差最大值和最小值所对应的色样的序号为1064和157。图6为具有色差最大值及最小值的重建光谱分布和所对应的原始光谱分布。

图6 具有色差最小值及最大值的重建和原始光谱分布
综上所述,1058号色样的均方误差是色样中最大的,但是色差却不是最大的;539号色样的均方误差是色样中最小的,但是色差也不是最小的。可见,均方误差只能在一定程度上解释重建误差的物理意义,当其值达不到0时,色差的评价更具有实际意义。
4. 结论
本文设计了以聚类分析和FICA算法的混合算法。并对此算法和PCA算法进行对比分析,得出利用混合算法重建的多光谱空间能够更好地表示原始光谱空间。但是由于本算法所应用的数据只是理想数据,有一定的局限性,以后可以将其应用到实际印刷色块,从而实现该算法的应用价值。
[1] 王莹,曾平.面向打印的光谱色彩管理中间空间构造方法[J].计算机科学,2010(5).
[2] 卫俊霞,相里斌,高晓惠,段晓峰.基于K-均值聚类与夹角余弦法的多光谱分类算法[J].光谱学与光谱分析,2011(5).
[3] Vasilescu M A O, Terzopoulos D. Multilinear independent components analysis: 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2005[Z]. San Diego, CA, United states: 2005: 547-553.
[4]王一帆,唐正宁. 基于PCA和ICA的多光谱数据降维方法[J]. 光学技术,2014(2).
[5]王莹,曾平,罗雪梅,谢琨.一种用于低维光谱空间构造的非负主成分分析法[J].四川大学学报(工程科学版),2010(2).
[6]Soize C. Construction of probability distributions in high dimension using the maximum entropy principle: Applications to stochastic processes, random fields and random matrices[J]. International Journal for Numerical Methods in Engineering. 2008, 76(10): 1583-1611.
[7]Hill B. Color capture, color management and the problem of metamerism: Does multispectral imaging offer the solution Proceedings of the 2000 Color Imaging: Device-Independent Color, Color Hardcopy, and Graphic Arts V[M]. San Jose, CA, USA: 2000: 2-14.
[8]刘武辉.印刷色彩学[M].胡更生.北京:化学工业出版社,2008.
[9]孔令罔,朱元泓,李琼.以混合算法建立宽带多光谱色彩表示空间[J].武汉大学学报(信息科学版),2006(9).
【责任编辑 马太来】
Abstrat: By using the cluster analysis method according to the spectral luminous efficiency functions, the linear dimensionality reduction in multispectral dataset was realized, and the independent components of the dimensionality reduction data were extracted by using the fast independent component analysis method. Then, the spectral space was reconstructed according to the independent components. Finally, contrast this method and the principal component analysis method from the mean square error and color difference. The experimental results showed that the average value of mean-square error of proposed method reduced by 3.64% and the average value of color difference increases by 24.08% in comparison with PCA. The multispectral space reconstructed by using hybrid algorithm can efficiently represent the original spectral space.
Research of Color Signal Multispectral Representation Space Based on Hybrid Algorithm
LI Mei1,KONG Ling-wang2
(1.DepartmentofMechanicalandElectricalEngineering,YunchengUniversity,Yuncheng044000,China)
(2.DepartmentofPrintingandPackage,WuhanUniversity,Wuhan430079,China)
Multi-spectral space; Cluster analysis;Independent component analysis; Mean square error; Color difference
2015-02-11
运城学院院级科研项目 (CY-2013021)
李梅(1987-),女,山西吕梁人,运城学院机电工程系教师,硕士,研究方向为色彩科学与应用。
TS801
A
1008-8008(2015)03-0029-05
