基于三角拓扑结构的指纹加密方案*

2015-06-23刘嘉勇汤殿华

通信技术 2015年3期

关键词：样板个数指纹

茹宇，刘嘉勇，汤殿华

(1.四川大学电子信息学院，四川成都 610064；2.保密通信重点实验室，四川成都 610041)

基于三角拓扑结构的指纹加密方案*

茹宇1，刘嘉勇1，汤殿华2

(1.四川大学电子信息学院，四川成都 610064；2.保密通信重点实验室，四川成都 610041)

模糊金库作为生物加密领域的经典算法已得到广泛应用。在模糊金库方案的基础上，提出一种基于三角拓扑结构的指纹加密方案。首先提取带有三角拓扑结构的指纹特征细节点，然后构造多元线性函数，将细节点映射到多元线性函数上，添加干扰集，生成指纹加锁集。在解锁时，比对样板细节点和模板细节点三角拓扑结构，对样板图像进行配准。实验结果表明，该方案解决了样板指纹需要提前配准的问题，同时很大程度上缩减了秘密信息恢复的时间，提高了系统的效率。

模糊金库三角拓扑多元线性函数

0 引言

随着信息技术和互联网技术的普及，信息安全成为人们关注的焦点。然而传统身份认证，由于用户口令或者钥匙容易被盗、丢失、复制，已经不能满足现代信息安全的需求。生物特征加密技术是将生物识别技术与密码学理论相结合，克服了传统身份认证的局限。在所有生物特征中，指纹的综合性能较高，已被得到广泛的应用。针对密钥产生或使用方式的不同，将生物特征加密分为密钥绑定、密钥释放和密钥生成三种方式[1]。而这三种方式，密钥绑定方式发展相对成熟。Jules等人在模糊承诺方案的基础上提出了模糊金库方案(Fuzzy Vault)[2]。在Jules等人工作的基础上，Liu和Wang 提出基于混沌序列的密钥绑定算法[3]。Uludag等提出了基于多项式的指纹Fuzzy Vault算法[4]，在加锁Vault和解锁Vault时都需要构造多项式。但是他们的方案中都存在不足：①匹配时，假设指纹图像已经配准，然而在实际应用中是不可能的；②恢复秘密信息的细节点的个数由多项式的阶决定，细节点数目过少，会导致系统错识率提高，从而增加非法用户获取签名密钥的风险[5]，而较多的细节点可以提供更高的安全性，然而高阶多项式系数求解的复杂度较高，恢复秘密信息比较耗时。

本文在原始Fuzzy Vault的基础上提出一种基于三角拓扑的指纹加密方案。提取带有三角拓扑结构细节点特征信息，通过分段秘密信息和伪随机数构造多元线性函数，生成加锁集，解锁时对细节点三角拓扑结构进行比对，匹配细节点，求解多元线性函数系数，恢复秘密信息。实验结果表明该方案克服了现有Fuzzy Vault方案需要预配准、求解多项式耗时的问题，提高了系统的安全性。

1 基于三角拓扑结构的指纹加密方案

由于位移，旋转，非线性失真，压力和皮肤状况等情况，同样手指的指纹可能不同，同时高阶多项式求解比较耗时。因此在加锁时，本文采用多元线性函数绑定指纹细节点和系统秘密信息。而在解锁时首先比对样板指纹和模板指纹的三角拓扑结构，对样板指纹进行配准，然后比对样板指纹细节点与模板指纹细节点的相似性，得到匹配细节点集合，恢复秘密信息。本文方案主要包括，指纹模糊金库加锁，指纹模糊金库解锁两个阶段，所有运算均在有限域GF(216+1)内进行。

1.1 指纹模糊金库加锁

模糊金库加锁主要通过构造多元线性函数绑定细节点和系统秘密信息，同时添加干扰点，隐藏真正的细节点。

(1)指纹特征细节点提取

指纹细节点的类型主要有端点、叉点、中心点和三角点。对模板指纹图像预处理，提取指纹特征细节点集合Tp={mi=(xi,yi,θi,tri1,tri2,tri3,ti)},其中，1≤i≤n，n为细节点个数，xi为指纹特征细节点的横坐标，yi为指纹特征细节点的纵坐标，θi为指纹特征细节点的方向场角度，ti为细节点的类型，tri1，tri2，tri3为细节点的三角拓扑结构。细节点mi的三角拓扑结构示意图如图1所示，具体提取过程如下：

1)提取细节点mi(1≤i≤n)的横、纵坐标xi,yi,，方向角θi以及类型ti。在此基础上以mi为圆心，以R为半径作圆。

2) 将细节点mi的方向角θi逆时针旋转45°，与圆周的第一个交点记为顶点1，此点的方向场角度记为tri1。

3)在顶点1为基础上，作该圆的内接正三角形，与圆周的交点依次记为顶点2和顶点3，方向场角度分别记为tri2，tri3。

细节点mi的三角拓扑结构由其内接正三角形三个顶点的方向角构成，tri1，tri2，tri3∈[0，180)。对超出图像表示范围的顶点，将其的方向角度均设为固定值255。

图1 细节点mi的三角拓扑结构示意

(2)构造多元线性函数

假设系统随机产生秘密信息K，长度一般为128 bit，需要d(d>8)个细节点来绑定秘密信息。

1)构造系数矩阵。将K从高位到低位，分割为8段，每段长度为16 bit，分别记为a7，a6，a5，a4，a3，a2，a1和a0。系数a8，…，a(d-2)为随机产生的16 bit数。连接a0～a(d-2)，计算连接值的CRC-16值记为a(d-1)。得到多元线性函数的系数矩阵记为A=[a0,a1,a2,a3,…,a(d-1)]。

2)产生多元线性函数，生成真实细节点集合。连接指纹模板Tp中细节点mi的xi和yi(1≤i≤n)，记为：gi=xi||yi；以gi作为种子，生成16 bit伪随机数分别记为ri1，ri2，…，ri(d-1)，令ri0=gi，mi参数向量记为：Ri=[ri0,ri1,…,ri(d-1)]，则第i个细节点的多元线性函数可用式(1)进行表示

(1)

式中，1≤i≤n，d为绑定秘密信息需要的细节点个数，f(Ri)为细节点mi在线性函数上的映射。连接所有细节点的横、纵坐标，并将其作为种子，生成16 bit伪随机数，得到其参数向量，通过式(1)得到所有细节点在线性函数上的映射，生成真实指纹细节点集合，记为:

Tpt={mi=(xi,yi,θi,tri1,tri2,tri3,ti),f(Ri)|1≤i≤n}

(3)产生干扰点集合

为了隐藏真实指纹细节点，产生大量的干扰点，干扰点的个数要远大于真实点个数，且与指纹细节点之间必须满足一个预设的距离阈值THd，同时干扰点必不能位于秘密信息K的编码多元线性函数上。

生成满足条件的干扰点集合记为

C={mj=(xj,yj,θj,trj1,trj2,trj3),βj}

其中1≤j≤n，βj≠f(Rj)，r(r>>n)为产生干扰点个数，βj∈(0,217-1)，θj∈(0,360)，trj1∈(0,360)，trj2∈(0,360)，trj3∈(0,360)和tj∈(1,2,3)。

(4)生成加锁集合

混合真实指纹模板加锁集Tpt和干扰点集合C，并置乱，形成模糊金库加锁集记为

Tptc=Tpt∪C={ms=(xs,ys,θs,trs1,trs2,trs3,ts)f(Rs)}

其中，1≤s≤n+r，n+r表示总数。

1.2 指纹模糊金库解锁

模糊金库解锁，通过用户提供的指纹样板，与指纹模板的模糊金库加锁集匹配，分离出干扰点，从中提取到真实细节点，恢复出系统秘密信息。

采用1.1节模板指纹细节点的提取方法，提取样板指纹细节点集合，记为

Fp={mj′=(xj′,yj′,θj′,trj1′,trj2′,trj3,tj′)}

其中，1≤j≤n′，n′表示样板细节点个数。

(1)样板细节点配准

首先，从指纹模板mi(1≤i≤n)与样板mj′(1≤j≤n′)中各任取一点，比较两个细节点的类型，若类型不同，则重新从指纹样板中取一细节点。

其次，比对两个细节点的三角拓扑结构相似性，即计算θi和tri1的方向场角度差C1=|θi-tri1|与θj′和trj1'的方向场角度差C1′=|θj′-trj1′|，以及三角拓扑结构中相互两个顶点之间的方向场角度差，如果mi和mj′对应角度误差均在预先设定的角度误差范围之内，则认为两个细节点的三角拓扑结构相似。若不相似，则重新从指纹样板中取一细节点，与指纹模板细节点比对三角拓扑结构是否相似。然后，对于相似的细节点，假设样板中第z个细节点mz′与模板中的细节点mi三角拓扑结构。相似则计算两个细节点的角度旋转量：Δθ=(θi-θz′)mod360、横坐标偏移量：Δx=xi-xz′、纵坐标偏移量：Δy=yi-yz′。通过式(2)对样板细节Fp点进行配准，配准后的指纹样板记为

Ap={mj″=xj″,yj″,θj″,trj1″,trj2″,trj3″,tj″}

其中，1≤j≤n′。

(2)

(2)指纹细节点匹配

指纹特征细节点匹配即指纹模板Tptc与配准后的指纹样板Ap中细节点的匹配，必须满足两个条件：

1)当两个细节点满足式(3)匹配条件时，认为此两点是匹配的

(3)

式中，Δθ、Δx、Δy和Ed分别表示当前两个细节点的夹角、水平距离、垂直距离和距离；THθ、THx、THy和THEd分别表示夹角阈值、水平距离阈值、垂直距离阈值和欧氏距离阈值。

2)当相互匹配的细节点个数及相似度均大于预先设定的合格阈值时，认为指纹样板与模板匹配成功，来自同一手指。得到匹配点集合记为TGmatch={xk,yk,f(Rk)}，其中，1≤k≤n，k为相互匹配的细节点个数。

指纹模板与配准后的样板之间的相似度说明了两组细节点集合比对的一致程度，记为SD

SD=4×score×k×maxpnum/(2n′)2

(4)

其中，maxpnum：表示最大指纹特征细节点个数；score表示分数，记录指纹模板与配准后样板上可能匹配的细节点之间，对应特征元素的相对误差大小累计情况。可建立如式(5)所示的关系：初始score=0。

score=score+(THθ-Δθ)+(THEd-Ed)

(5)

设相似度SD的合格阈值记为THSD，细节点匹配个数为绑定秘密信息的细节点个数为d，只有匹配的细节点个数k≥d，相似度SD≥THSD，则认为样板指纹匹配成功。

(3)重构多元线性函数，恢复秘密信息K

假设，恢复秘密信息需要d个细节点，从匹配点集合TGmatch中任选d个点作为候选点集。令gk=xk‖yk,(1≤k≤n)，以gk作为种子产生16 bit伪随机数分别记为rk1，rk2，…，rk(d-1)，令rk0=gk。对于每个细节点的gk，都会得到细节点mk参数向量记为

Rk=[rk0,rk1,…,rk(d-1)]

对于每组细节点候选集，通过式(6)可以得到多元线性方程组

(6)

令f=[f(R0),f(R1),…,f(R(d-1))]T，

A′=[a0′,a1′,…,a(d-1)′]，

则多元线性方程可以表示为

f=A′Rmod65537，

(7)

由于作为种子的gk各不相同，所以得到的参数向量矩阵每行互不相关，即行列式|R|≠0，则可得到A′=fR-1mod65537。

将a0′，a1′，…，a(d-2)′连接起来，计算连接值的CRC-16值，如果该值等于a(d-1)′，则秘密信息

k=a7′‖a6′‖a5′‖a4′‖a3′‖a2′‖a1′‖a0′，解锁成功。反之，则需要从匹配点集合TGmatch中在另选d个点重新构造多元线性函数。若遍历完匹配点集合中的所有组合都不能恢复出秘密信息，则说明匹配点集合中假细节点数量过多。

2 实验结果与安全性分析

2.1 实验结果分析

为了验证本方案的准确性和有效性，本文利用公开指纹库FVC2004-DB2中的来自100个不同手指的800幅图像测试评估该方案性能。指细节点平均个数为35，添加干扰点个数300。本文将两个细节点三角拓扑的角度误差设置为8，匹配条件阈值参数为：夹角阈值THθ=10、水平阈值THx=10、垂直阈值THy=10、距离阈值THEd=10，相似度阈值THSD=100。

对于真匹配，用指纹库中同一手指的每一个图像和余下图像进行比较，进行2 800次真匹配；对于假匹配，取每个手指中细节点个数最多的指纹图像与其余来自不同手指的图像比较，进行74 250次假匹配测试。依次测试匹配细节点个数9到13对应的指纹匹配拒识率(FRR)和误识率(FAR)，并计算该方案恢复秘密信息需要的时间。

通过表1可以看出随着匹配时需要细节点个数的增多，误识率FRR逐渐增大，拒识率FAR逐渐减。

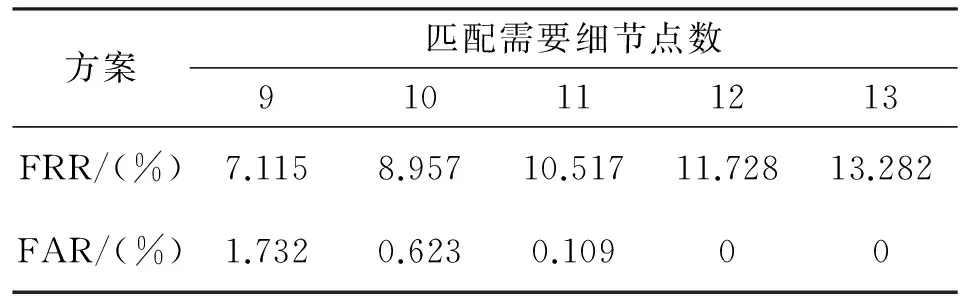
表1 不同匹配细节点个数的匹配结果

通过表2可以看出，本文采用构造多元线性函数方案较Uludag等人构造多项式方案大大缩减了时间，因为重构高阶多项式的计算比较费时。

表2 比较不同方案恢复秘密信息的平均时间

2.2 安全性分析

本文在构造线性函数时，引入随机数，相对于传统的模糊金库方案，函数的阶数不在由秘密信息的长度决定，而是可以根据要采用的匹配细节点的个数来调节，很大程度上提高了系统的安全性。

由于真实指纹细节点中添加了大量的干扰点，起到对真实点隐藏的作用，如果攻击者要从Fuzzy Vault中分离真实细节点比较困难。同时对于恢复秘密信息需要的细节点数越多，攻击者破解秘密信息的难度也就越大。对于暴力破解，假设攻击者没有真实指纹的数据，用本文方法来计算攻击者需要尝试的次数。文献[6]指出，只有12个以上的细节点匹配才是可靠的，因此，取d为13。平均细节点个数为35，干扰点个数为300，则攻击者需要尝试的次数T为:

相当于攻击者要破解24个字母和10个数字随机组合的10位数的次数(3410≈2.06×1015)，所以暴力破解的难度也是比较大的。

3 结语

本文以指纹三角拓扑结构为基础，采用多元线性函数绑定秘密信息，匹配时并未对活体指纹样板进行提前配准操作，而是在解锁过程中通过对比三角拓扑关系实时配准，得到相互匹配的点对，从而恢复出秘密信息，这在一定程度上改善了提前配准问题。同时实验结果表明，该方案在很大程度上缩减了恢复秘密信息的时间，提高了效率。然而在指纹模安全性方面还需要进一步提高。

[1] 李鹏，田捷，杨鑫.生物特征模板保护[J]. 软件学报，2009，20(06):1553-1573. LI Peng, TIAN Jie, YANG Xin. Biometric Template Protect [J] Journal of Software 2009，20(06):1553-1573.

[2] Juels A,Sudan M. A Fuzzy Vault Scheme[J]. Designs, Codes and Cryptography, 2006, 38(2): 237-257.

[3] Hong-wei L,Yao W. A New Fuzzy Fingerprint Vault Using Multivariable Linear Function based on Lorenz Chaotic System[C]//Computer Science and Automation Engineering (CSAE), 2012 IEEE International Conference on. [s.l.]:IEEE, 2012: 531-534.

[4] Uludag U,Pankanti S,Jain A K. Fuzzy Vault for Fingerprints[C]// Audio-and Video-Based Biometric Person Authentication.[s.l.]:Springer Berlin Heidelberg,2005:310-319.

[5] 李丹, 卿昱, 谭平嶂. 一种基于生物特征加密技术的数字签名方案[J]. 通信技术, 2010，43 (02): 128-130. LI Dan, QING Yu, TAN Ping-zhang. A Digital Signature Scheme based on Biometric Encryption[J]. Communications Technology, 2010,43(02):128-130.

[6] Pankanti S, Prabhakar S, Jain A K. On theIndividuality of Fingerprints[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on,2002,24(8):1010-1025.

RU Yu(1987-), male , M.Sci. , mainly working at network communication and network security.

刘嘉勇(1962—)，男，教授，博士，主要研究方向为信息安全理论与应用、网络通信与网络安全；

LIU Jia-yong(1962-), male, professor, Ph.D., principally working at theory and application of information security, network communication and network security.

汤殿华(1986—)，男，硕士，主要研究方向为信息安全理论与应用。

TANG Dian-hua(1986-)，male， M.Sci., mainly working at theory and application of information security.

Fingerprint Encryption Scheme based on Triangle Topology

RU Yu1，LIU Jia-yong1，TANG Dian-hua2

(1.College of Electronic and Information Engineering, Sichuan University, Chengdu Sichuan 610064, China;2.Science and Technology on Communication Security Laboratory,Chengdu Sichuan 610041, China)

Fuzzy vault, as a classical encryption algorithm, is widely used in biometric encryption. Based on Fuzzy Vault scheme by Jules et al., this paper proposes a fingerprint encryption scheme triangular topology. Firstly, the fingerprint minutiae feature with a triangular topology is extracted, and then multiple linear functions are constructed,finally, the minutiae is mapped onto multiple linear functions, the inteference set added,and the fingerprint locking set generated. Sample image is registrated by comparing triangle topology of sample minutiae with template minutiae during the unlocking process. Experimental results show that this scheme could solve the advanced registration of sample fingerprint while greatly reducing the time for secret information recovery, thus the system efficiency is improved.

fuzzy vault; triangular topology; multiple linear function

date:2014-09-11；Revised date：2014-12-30

TP309

1002-0802(2015)03-0362-05