机载预警雷达搜索参数研究

李相如,曹 晨

(中国电子科学研究院,北京 100041)

工程与应用

机载预警雷达搜索参数研究

李相如,曹 晨

(中国电子科学研究院,北京 100041)

针对相控阵体制机载预警雷达搜索参数设计问题,从雷达威力方程出发,分析了波束编排及波位脉冲积累时间计算方法,并对全向搜索模式和扇区搜索模式不同设计约束条件下的搜索参数求解方法和求解步骤进行了研究。仿真计算对扇区模式搜索参数计算方法和步骤进行了验证,为工程应用提供了有益参考。

机载预警雷达；探测距离；搜索时间

0 引 言

机载预警雷达从第二次世界大战末期诞生以来，已经走过了60多年历史，其主要任务是为了解决低空目标探测盲区问题。随着技术的进步，机载预警雷达面临的电磁环境日益复杂，具有高空、高速和低雷达散射截面积（RCS）等特性的目标不断涌现，给机载预警雷达带来了严峻挑战。为了适应未来复杂战场环境，机载预警雷达不仅需要采用诸如STAP处理，认知等新技术来提高其探测性能，同时对其工作模式设计也提出了更高要求，特别需要根据不同方向的威胁等级和载机的位置，动态设置搜索扇区宽度和搜索时间，以适应未来复杂战场环境。

机载预警雷达搜索模式下参数设计需要满足威力和时间的要求，文献[1]对相控阵雷达的搜索参数进行了研究，重点对多目标条件下跟踪和搜索时间分配进行了讨论，本文在文献[1]基础上对采用相控阵体制机载预警雷达的波位编排与搜索时间和探测威力参数计算进行详细分析并给出计算方法和计算步骤。

1 机载预警雷达搜索模式主要战术技术指标

1.1 机载预警雷达搜索威力方程

经典雷达搜索威力方程为[2]：

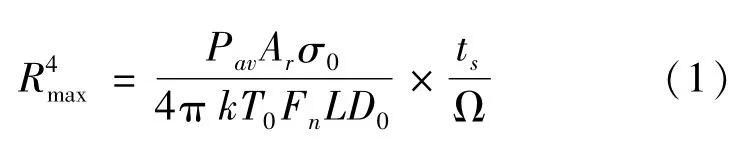
其中Pav为雷达平均发射功率；Ar为接收天线孔径有效面积；σ0为目标雷达散射截面积；k为波尔兹曼常数；T0为热力学温度；Fn为接收机噪声系数；L为系统总的损耗；D0为最小可检测信噪比；ts为搜索时间长度；Ω为雷达搜索空域立体角宽度。

根据方程（1），雷达搜索模式下，搜索空域宽度Ω和搜索时间长度ts一旦确定，对常规目标的探测威力主要取决于功率孔径积。

对于机载预警雷达，由于其天线俯仰波束宽度一般能满足高度覆盖要求（俯仰上可能存在能量浪费），常采用方位一维扫描方式，其搜索模式下威力方程为：

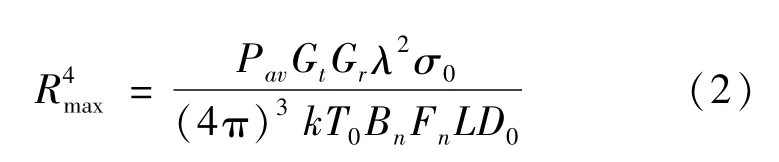
由于机载预警雷达为了对抗地杂波，一般采用PD体制，式中多普勒滤波器宽度Bn等于目标所在波位相参积累时间长度的倒数。

假设搜索空域宽度Ω≈φc×θc，φc为俯仰宽度，θc为方位宽度。雷达主瓣俯仰波束宽度为△φ1/2，方位宽度为△θ1/2。当机载预警雷达俯仰波束宽度满足高度覆盖要求，即△φ1/2≈φc时，搜索空域宽度可表示为

根据上式，可由经典搜索威力方程（1）推导出机载预警机雷达搜索威力方程（2）。

对于同一部机载预警雷达，不同的方位扇区大小和搜索时间长度，最终体现在方程（2）中多普勒滤波器宽度Bn指标的差异。

如果机载预警雷达采用机械扫描方式，则雷达天线增益和波束宽度在360°内保持不变（不考虑机身对天线方向图的影响），因此各方向多普勒滤波器宽度相等；而当机载预警雷达采用相控阵电扫描方式，由于雷达波束偏离法向后，波束会逐渐展宽，天线增益将下降，因此各波位多普勒滤波器宽度将不同。如果各波位采用等威力设计，则可用雷达法向天线增益和多普勒滤波器宽度计算雷达探测威力。

相控阵体制机载预警雷达搜索模式多普勒滤波器宽度的计算，需要确定搜索空域所需的波位数和单个波位的时间分配。

1.2 波位编排

相控阵体制机载预警雷达在方位向进行一维扫描，一般采用2 dB波束交叠进行波位编排，但天线波束宽度会随扫描角的增大而展宽，因此需要计算各波位指向和波束宽度才能完成波位编排。假设法向2 dB波束宽度为θB，0，以法向波位为参考，偏离法向的第n个波位波束宽度为θB，n，波束中心指向角为θn，则

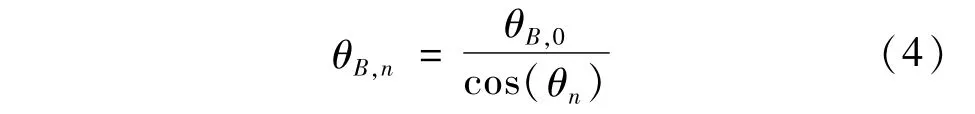
第n个波束与第n-1个波束之间关系为

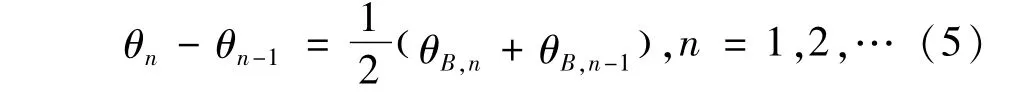
将式（4）代入式（5），可得到关于θn的超越方程，该超越方程的解可近似表示为[3-4]

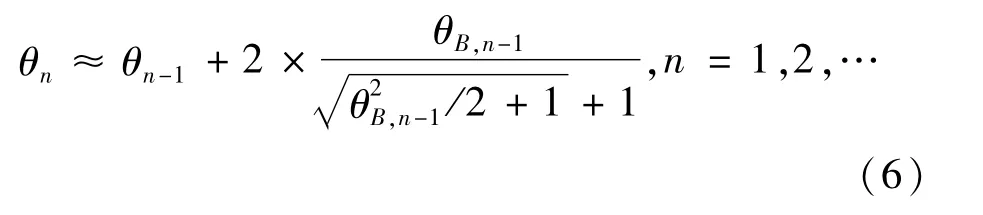
已知法向波位波束宽度θB，0，对于给定的方位扫描范围，例如[-θc/2，θc/2]，根据式（6）和式（4），利用计算机可完成波位编排。

1.3 波位脉冲积累时间

雷达的天线增益与天线俯仰和方位波束宽度关系可近似表示为[5]

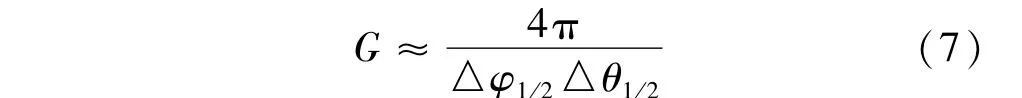
对于在方位向进行一维扫描的相控阵体制机载预警雷达，其俯仰向波束宽度保持不变，方位向波束宽度与波束指向角的余弦成反比，如式（4）所示，因此相对于法向波位天线增益G0，第n个波位天线增益可近似表示为

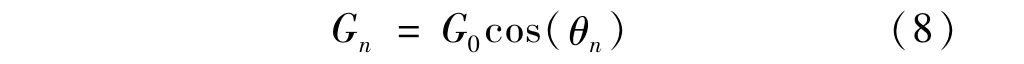
由搜索威力方程（2），雷达接收端回波信噪比与天线收发增益GtGr和脉冲积累时间τn成正比，即

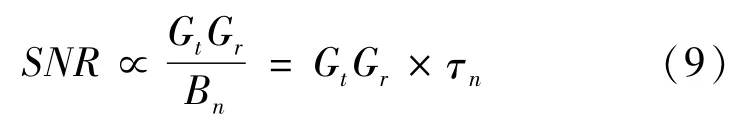
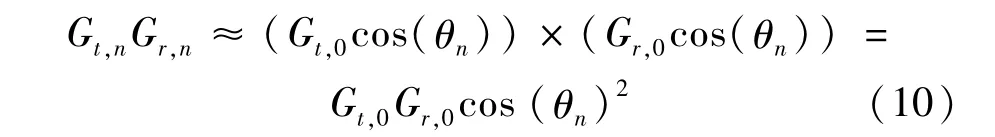
根据式（8），第n个波位天线收发增益可近似表示为Gt，0和Gr，0分别表示法向天线发射和接收增益。

为了补偿由于波束展宽导致的接收信号信噪比下降问题，需要增加波位的脉冲积累时间长度，假设法向波位脉冲积累时间长度为τ0，则当时，可实现机载预警雷达各搜索波位的探测威力相等。

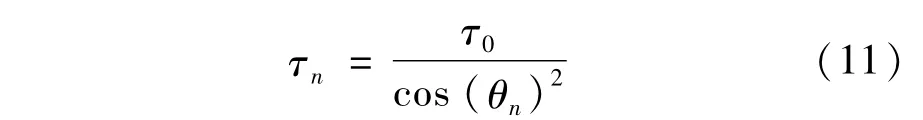
2 搜索参数设计

2.1 全向搜索模式

假设相控阵雷达由于受阵元间互耦效应等因素影响，单个阵面的扫描范围一般限制在[-60°，+ 60°]，扫描时间长度为ts。

根据公式（6），利用计算机按2 dB波束交叠对方位扫描[-60°，+60°]内进行波位编排，假设波位编排结果为[-60°，+60°]内需M个波位。需要注意的是，在进行波位编排时，由于单个阵面的方位向搜索范围关于阵面法线左右对称，因此只需分析一侧的波位编排便可求出整个[-60°，+60°]范围内的波位编排结果；另外，左右两侧波位编排均以法向波位为起始，到两侧±60°可能存在波位溢出问题，即两侧边缘波位覆盖范围超过±60°，实际工程中可适当对波位进行调整来解决。

接下来计算每个波位的脉冲积累时间分配。由于每个波位进行脉冲积累需要填充脉冲，如果雷达设计探测威力为Rt，完成一次脉冲积累的脉冲填充时间为2×Rt/c，c为电磁波传播速度。如果每个波位为了解距离和速度模糊需进行K组脉冲参差，则M个波位所需总的脉冲填充时间[6]

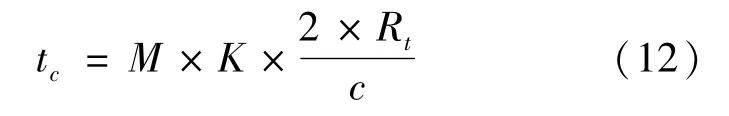
则单阵面可用于进行目标探测的有效时间为

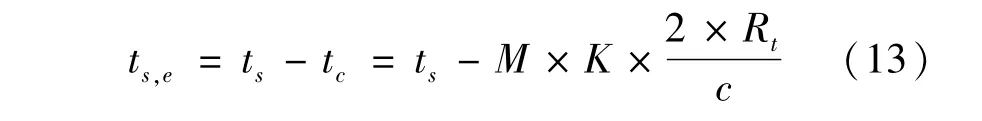
假设第n个波位各参差脉组的平均积累时间长度为τn，则总的脉冲积累时间为

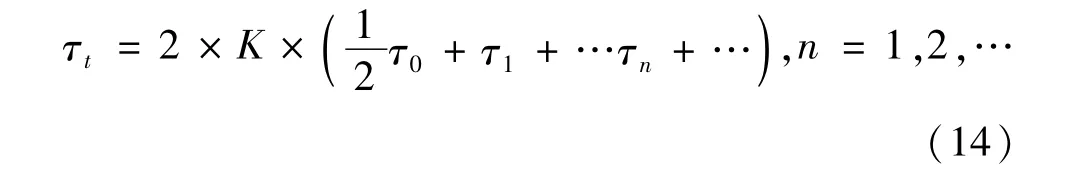
上式右侧括号外乘2是因为式（14）右侧括号内只计算了法线一侧波位脉冲积累时间；括号内第一项除以2，是因为法向起始波位只有一半宽度位于单侧扇区。

为了实现全向探测威力相等，各波位的脉冲积累时间需满足式（11），将式（11）代入（14），总脉冲积累时间可表示为

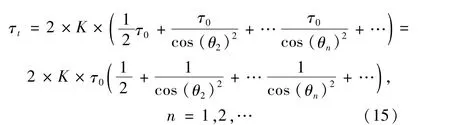
经过计算，可以得到总脉冲积累时间τt与法向波位脉冲填充时间τ0的函数关系。

由于总脉冲积累时间τt最大等于单阵面可用于进行目标探测的有效时间ts，e，因此根据式（15）和式（13），可以求出法线波位最大脉冲积累时间为

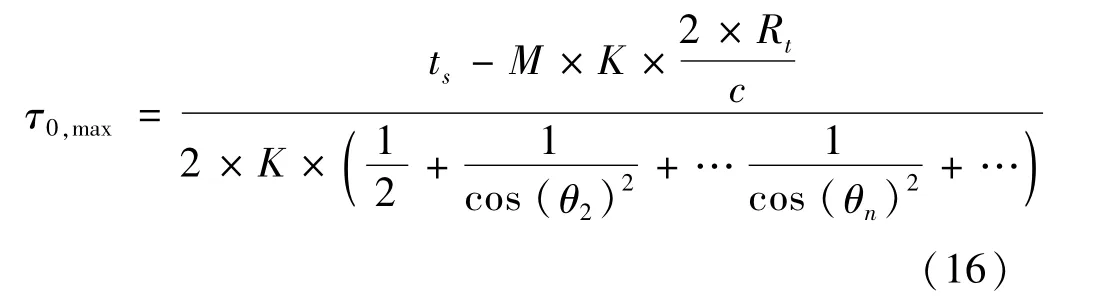
PD处理法向波位多普勒滤波器宽度Bn= 1/τ0，max，根据天线法向收发增益，利用式（2）可求出全向等威力条件下机载预警雷达搜索模式最大探测距离Rmax。

2.2 扇区搜索模式

雷达为提高对特定方向低RCS目标的探测能力，例如巡航导弹，隐身战机等，将搜索范围将从[-60°，+60°]缩小到一个小扇区，一般扇区宽度小于60°，同时增加搜索时间，这样将增加单个波位的脉冲积累时间，提高对低RCS目标的探测概率。机载预警雷达扇区搜索模式的扇区中心指向需根据平台运动和低RCS目标来袭方向进行动态调整。

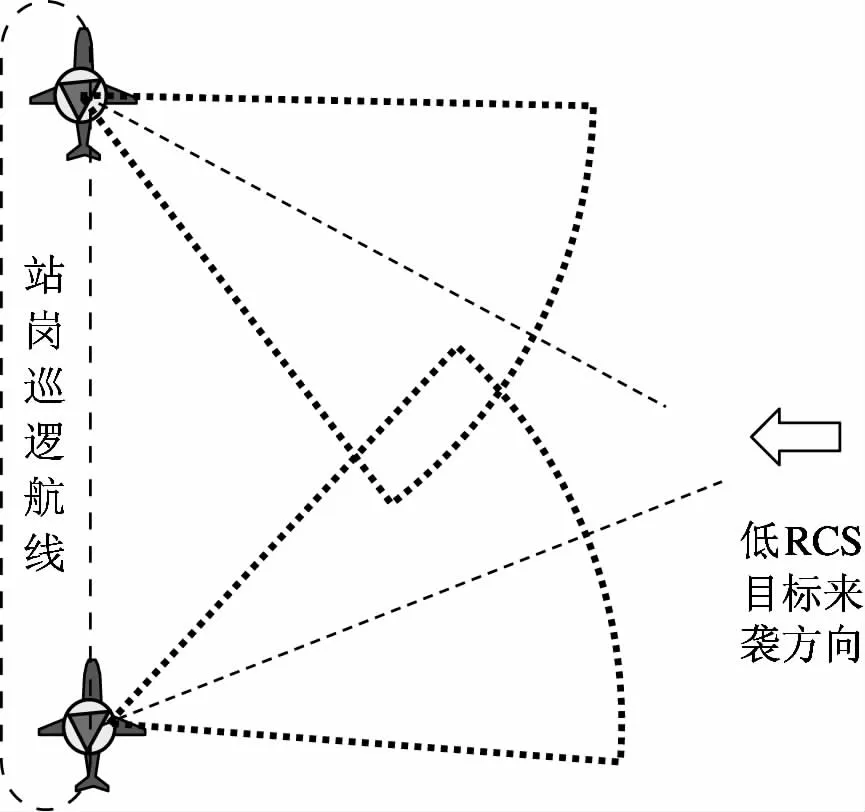
图1 扇区中心指向随载机运动变化示意图

（1）等数据率

等数据率是指搜索扇区因载机运动而在[-60°，+60°]范围内进行变化时，其数据率保持不变，但不同扇区中心指向，探测威力将不同。实际设计中在给定扇区宽度，搜索数据率条件下，需求出不同扇区中心指向角的探测距离。

假设搜索小扇区的宽度θB，s，扫描时间周期为ts。首先计算扇区中心指向不同角度时扇区内的波位编排。

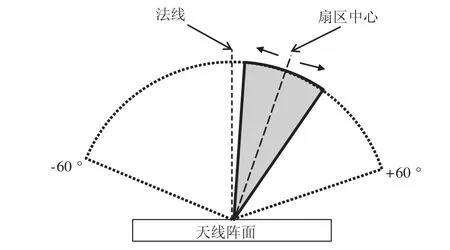
图2 扇区中心指向变化示意图

扇区搜索模式下，由于扇区的中心指向需根据平台位置进行动态调整，因此扇区不具有关于阵面法线对称的性质，这样需要对公式（6）进行适当修改。

假设扇区中心指向角为θsc，则其取值范围为

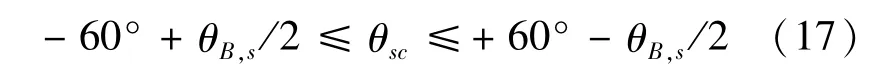
对于给定的扇区中心指向角θsc，已知法线方位波束宽度为θB，0，以扇区内最左侧波位作为波位编参起始波位，其指向角为

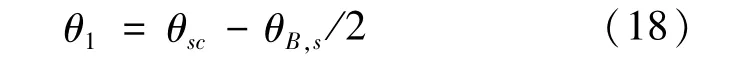
左侧起始波位宽度为

求出起始波位的指向角和波位宽度后，可以根据式（6）完成扇区内其它波位的编排。

接下来计算扇区内各波位的脉冲积累时间分配。假设法线波位脉冲积累时间为τ0，根据扇区内各波位探测威力相等原则，扇区内各波位总的脉冲积累时间为

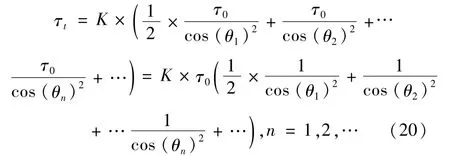
上式中括号内第一项除以2，是因为左侧起始波位只有一半位于扇区内。

根据式（16），可以求出法线波位最大脉冲积累时间

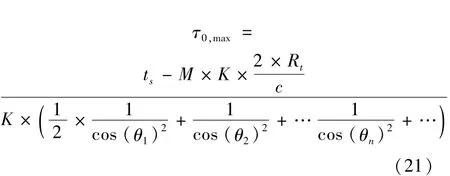
已知法向波位收发天线增益，因此可以用式（2）求出法向波位探测距离。需要注意的是，虽然法线波位不一定位于搜索扇区内，但由于求解τ0，max是以扇区等探测威力为原则，以法向波位为计算参考，因此可以求解的法向波位探测距离代替扇区内各波位的探测距离。

（2）等探测威力

等威力是指搜索小扇区中心指向随载机平台运动而变化时，探测威力保持不变，但不同扇区中心指向，数据率将不同。

假设探测距离要求为Rt，根据这一参数需要求出扇区中心指向不同角度所需的数据率。

首先，利用脉冲积累时间与多普勒滤波器宽度成倒数关系，根据式（2）求出法向波位在探测距离为Rt的约束条件下所需的脉冲积累时间τ0

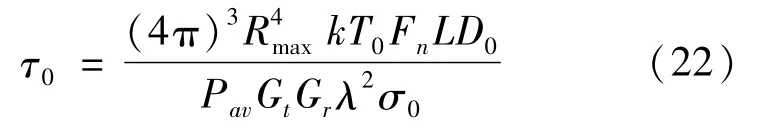
其次，对于中心为任意指向扇区，根据等数据率一节分析，利用公式（18）和公式（19）对其进行波位编排，假设波位编排结果为Mx。由于各扇区探测威力相等，因此可以根据式（22）求得的法向波位脉冲积累时间τ0，利用式（20）求出扇区内各波位所需总的脉冲积累时间τx。

这样对于中心为任意指向扇区，当探测距离为Rt，所需数据率为

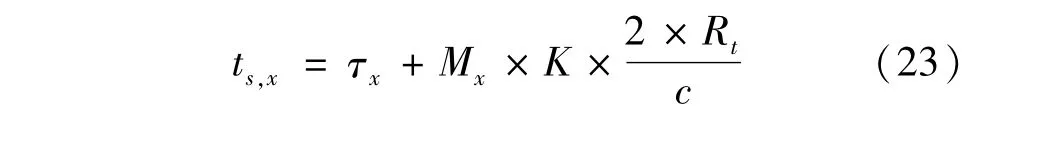
3 仿真分析

以下重点对扇区搜索模式等数据率和等威力两种情况进行仿真分析。

（1）等数据率

假设机载预警雷达工作频率为3 GHz，搜索扇区宽度为10°，搜索数据率为5 s，发射天线法向增益为34 dB，主瓣2 dB波束宽度为0.72°，参差脉组数为5，不考虑天线自身互耦等非线性因素对不同扫描角天线增益的影响，根据扇区模式等数据条件下公式（17）至（21），对波位编排并求出法向波位脉冲积累时间，进而求出不同扇区中心指向角的雷达探测威力，计算仿真结果如图3所示。

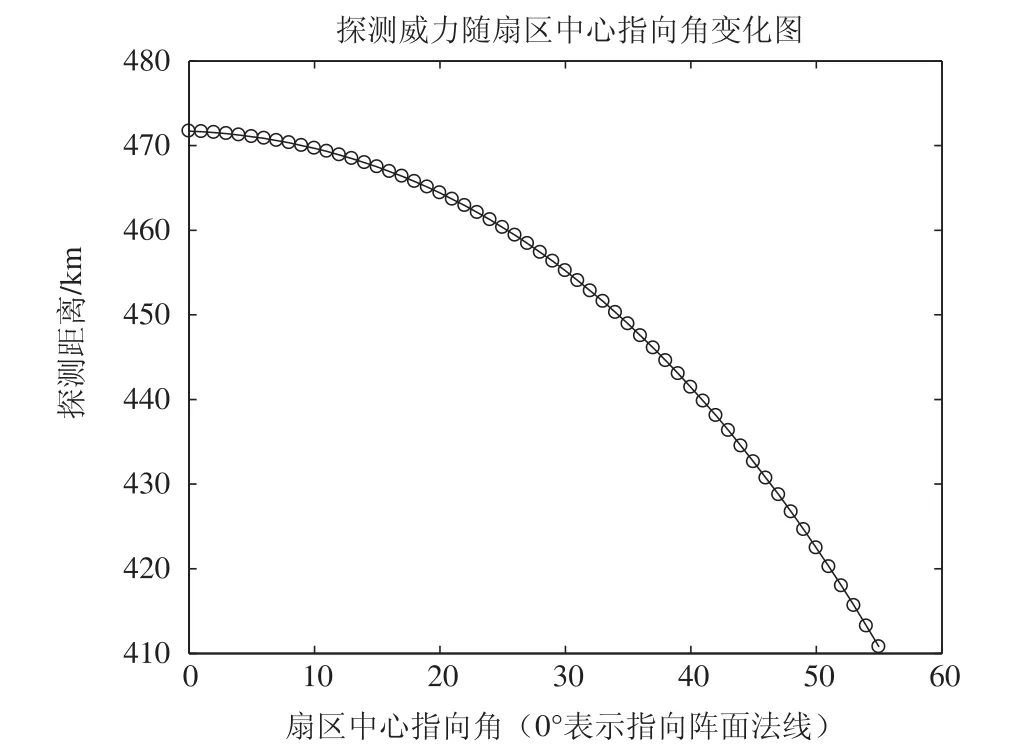
图3 等数据率条件下探测威力与扇区中心指向角变化关系仿真结果

根据上图仿真结果，当扇区中心指向两侧±55度时，探测距离将下降13%，探测性能下降明显。

（2）等探测威力

前面扇区搜索模式等数据率的仿真计算中假设不同中心指向扇区的数据率均为5 s，以下在前面仿真计算基础上，假设不同中心指向角扇区的探测威力均为470 km，根据式（22）和（23）仿真计算不同中心指向角扇区所需搜索时间，如图4所示。根据仿真计算结果，当扇区中心指向两侧±55度时，为了保持探测威力不下降，搜索时间由法向5 s增加到8.7 s，时间增加了 2.4 dB，折算到距离增幅为12.9%，与前面等数据率仿真计算结果中两侧±55度探测距离下降幅度完全吻合。

4 结 语

针对相控阵体制机载预警雷达搜索参数设计问题，首先从雷达威力方程出发，分析了波束编排及每个波位脉冲积累时间计算方法。在此基础上，对全向搜索模式和扇区搜索模式不同条件下的搜索参数求解方法和求解步骤进行了研究。最后，仿真计算验证了扇区模式搜索参数计算方法和步骤的正确性。

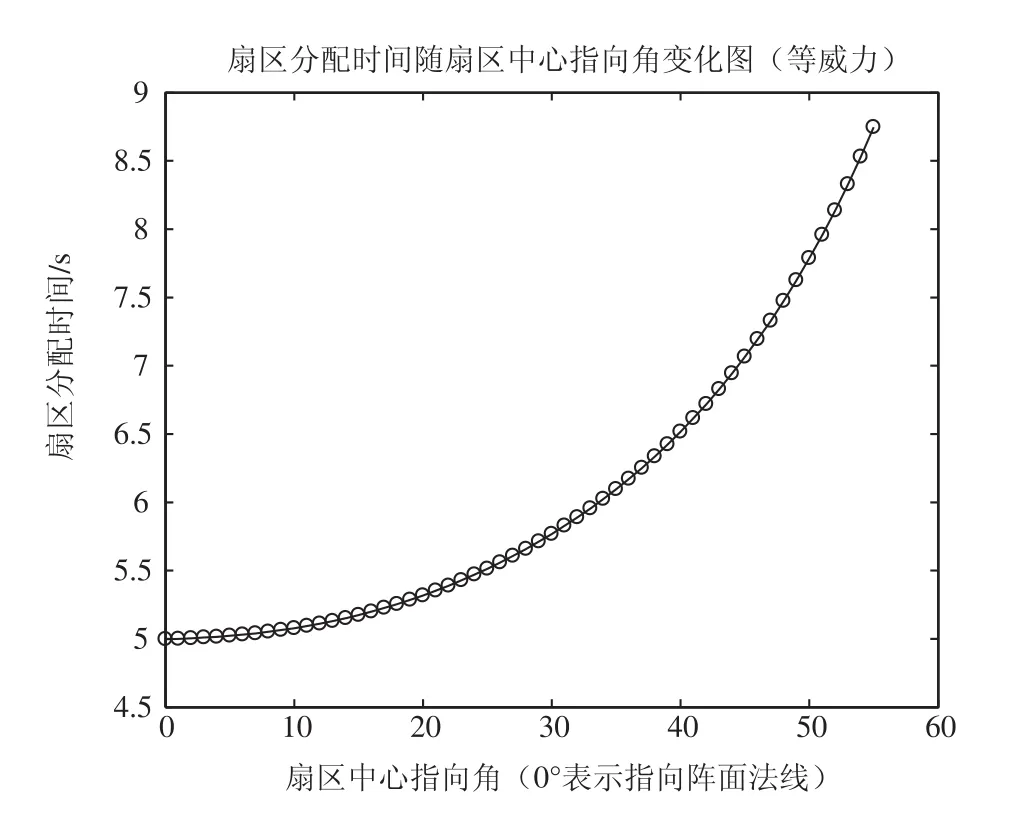
图4 等威力条件下扇区搜索时间与扇区中心指向角变化关系仿真结果

[1] 张立韬，李盾，王国玉.相控阵雷达搜索参数研究[J].现代雷达，2008（10）：20-25.

[2] 张光义，赵玉洁.相控阵雷达技术[M].北京：电子工业出版社，2006

[3] 王雪松，汪连栋，肖顺平，等.相控阵雷达天线最佳波位研究[J].电子学报，2003（06）：74-78.

[4] 钟广海，王克宇.相控阵雷达扫描波位和扫描时间的设计与优化[J].上海航天，1999（05）：32-36.

[5] 王峰，傅有光.数字相控阵与模拟相控阵雷达的性能对比分析[J].中国电子科学研究院学报，2012（02）：148-153.

[6] 曹晨，王小谟.机载相控阵PD雷达性能分析中的重要问题[J].现代雷达，2008（06）：14-16.

李相如(1984—),男,湖南益阳人,工程师,博士,主要研究方向为传感器系统设计；

E-mail：xiangruli2006@163.com

曹 晨(1974—),男,湖北当阳人,研究员,博士,博士研究生导师,主要研究方向为信息系统总体设计。

The Research on Airborne Early W arning Radar Search Parameters

LIXiang-ru，CAO Chen
（China Academy of Electronics and Information Technology，Beijing 100041，China）

Aiming at the problem of search parameters design of Early Warning Phased array radar，the selection principle and method of a number of search parameters are presented from the perspective of radar equation，including search time，detection range and beam-positon arrangement.The calculation method and process of the search parameters are analyzed according to the width of search space and precondition.A simulation is constructed to validate the calculation method of parameters of sector search model.

airborne warning radar；search range；search time

TN958.92

A

1673-5692（2015）04-406-05

10.3969/j.issn.1673-5692.2015.04.014

2015-04-08

2015-07-13

空军十二五装备预先研究项目（10206）