基于节点导纳法的多导体传输线串扰研究

2015-06-23王川川曾勇虎

中国电子科学研究院学报 2015年4期

关键词：传输线干扰源导体

王川川,曾勇虎,蒙洁

(电子信息系统复杂电磁环境效应国家重点实验室,洛阳 471003)

基础理论

基于节点导纳法的多导体传输线串扰研究

王川川,曾勇虎,蒙洁

(电子信息系统复杂电磁环境效应国家重点实验室,洛阳 471003)

为了研究多导体传输线的串扰变化规律,基于传输线分布参数节点导纳法和快速傅里叶逆变换技术,推导得到了多导体传输线串扰响应的计算公式,并根据具体算例,与其他方法对比验证了本文所用方法计算结果的正确性。基于所推导公式,仿真计算并分析了干扰源上升、下降沿时间,干扰源脉宽,电缆长度以及电缆材料参数对多导体传输线串扰的影响。研究结论对于了解多导体传输线的电磁脉冲响应规律及电磁防护具有一定参考意义。

节点导纳法；多导体传输线；串扰；快速傅里叶逆变换

0 引言

当两传输线并行接近时，强信号线主扰回路上的电压或电流将通过容性和感性耦合，在弱信号线被扰回路中产生感应电压或感应电流，从而对被扰回路中的信号产生影响。串扰便是并行回路间耦合影响的典型问题。因此，确定被扰回路上的感应电压和电流一直是研究的热点。例如对于军用移动电站来说，它与装备之间的连接电缆为非屏蔽多导体电缆，当军用移动电站的发电机某一相或两相发生故障，或外界电磁脉冲对电缆进行干扰时，高频信号沿电缆传播，可能使电能质量下降，对装备性能发挥造成影响，或对电站造成破坏。因此，必须研究多导体电缆芯线之间的串扰，了解电站遭受干扰的规律，以采取合理的防护措施。

对于多导体线缆之间的串扰有两类研究方法：理论仿真和实验研究。理论仿真方面，主要采用的方法有：时域有限差分（Finite-Difference Time-Domain，FDTD）法[1]，节点导纳分析法[2]，传输线理论[3]，传递函数法[4]，矩量法与传输线混合算法[5]，简化三维全波算法[6]，多导体传输线模型[7]，时域有限积分法[8]，时域BLT（Baum-Liu-Tesche）方程法[9][10]。文献中采用的FDTD等数值方法、全波算法虽然能够获得传输线串扰的计算结果，但建模方法复杂，计算时间较长。而节点导纳分析法计算简便，计算时间代价小，可用于分析串扰问题。

本文首先基于分布参数节点导纳法推导了多导体传输线串扰响应的计算公式，然后通过一个实例将本文算法与文献算法计算结果对比以验证方法的正确性，在此基础上研究了多导体传输线串扰的变化规律。

1 多导体传输线串扰的研究模型及方法

1.1 基于节点导纳法的串扰研究模型

串扰研究电路网络方程的形成基于改进节点法（Method of Nodal Admittance，MNA），每一个多端口元件都可对应主矩阵中的一个子矩阵[2]。多导体互连线可以看成一个子网络。下面，我们推导离散频变等效电路参数多导体互连线所组成的网络的MNA方程。

多导体传输线串扰研究模型如图1所示。图中，1、2、3、4、5、6分别为传输线感应信号各观测点。

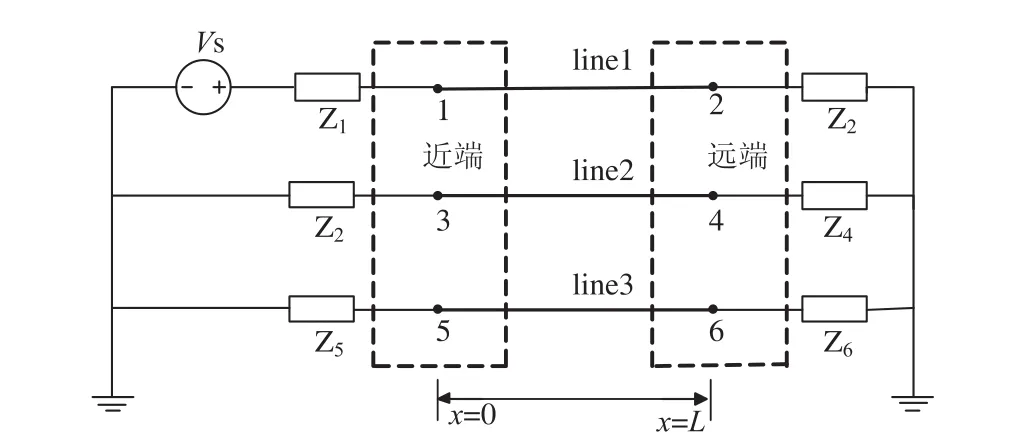
图1 多导体传输线串扰研究模型

假定传输线沿长度方向均匀，则在频域端口电压电流满足电报方程[11]：

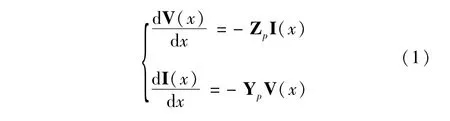
可得到传输线波动方程

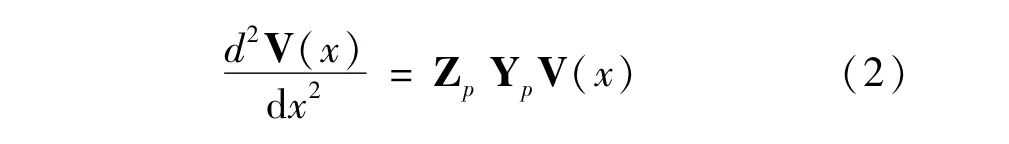
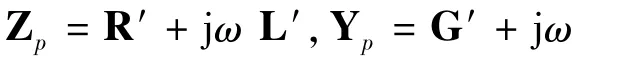
式中，Y为端接阻抗和不带端接阻抗的节点导纳矩阵组成的矩阵[2]，V为图1中所标示各观测点处的感应电压矩阵，I为各端接负载处外接激励源与负载共同作用产生的激励电流矩阵。

不带端接阻抗的节点导纳矩阵为[2]：

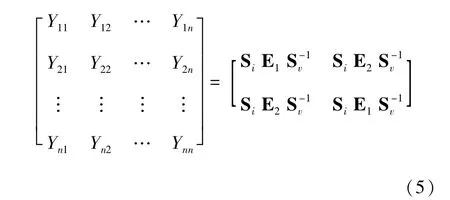
式中，n为传输线系统中信号线个数的两倍，例如以地面为信号参考回路的三导体传输线系统，则n=6。Sv是ZpYp特征值对应的特征向量组成的矩阵：

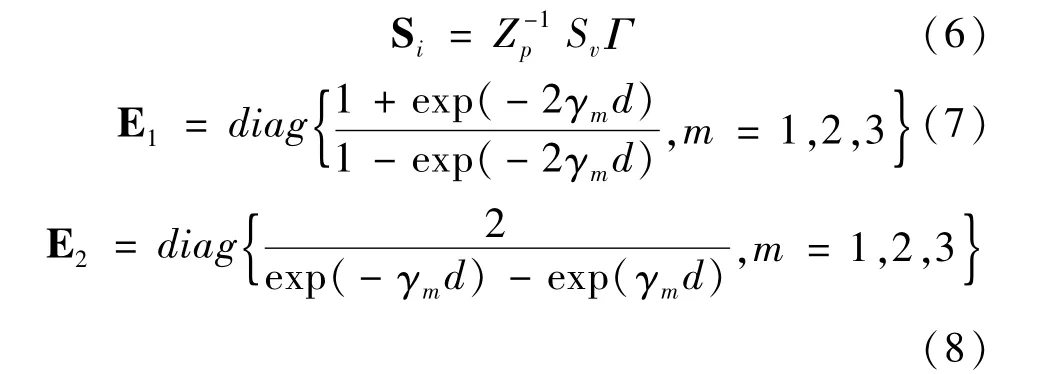
其中，diag表示矩阵为对角阵，d表示传输线长度，Γ为ZpYp的特征值开方后所组成的对角矩阵，γm为对角矩阵中对角线上的数值。由式（3）-（4），可得具有端接阻抗的传输线节点导纳方程为：

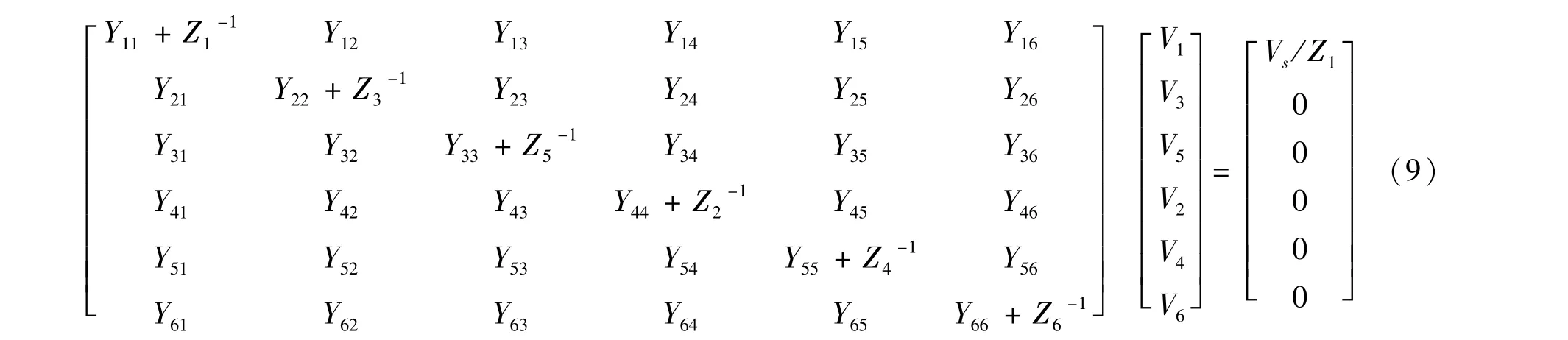
式中，[V1V3… V6]T为感应电压向量，[Vs/Z10…0]T为激励电流向量。式（9）即为多导体传输线串扰电压响应计算公式。这样，在每一个预先给定的频率点上就可以得到互连电路的网络方程，求解电路方程，得到多导体传输线串扰响应频域表达式，然后利用快速傅立叶逆变换技术（inverse fast Fourier transform，IFFT）对其进行逆变换就可求得时域响应。

1.2 方法验证

为了验证本文方法的正确性，我们采用本文方法对文献[4]所给算例进行重新计算。文献[4]采用长度为L=0.1m的双导体耦合线作为研究的对象，如图2所示，接地板未画出。线的分布参数为

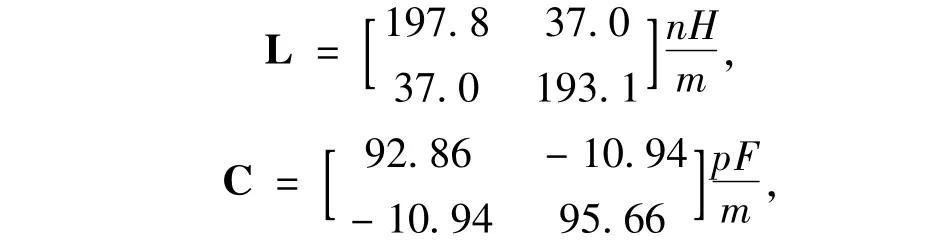
G=0。互连线1的左端受梯形电压波激励，上升和下降时间都为0.5 ns，顶部持续时间为1 ns，持续电压值为1.0 V。互连线左端的阻抗值Z1=Z3= 50Ω，右端的电容值C1=C2=1 pF。

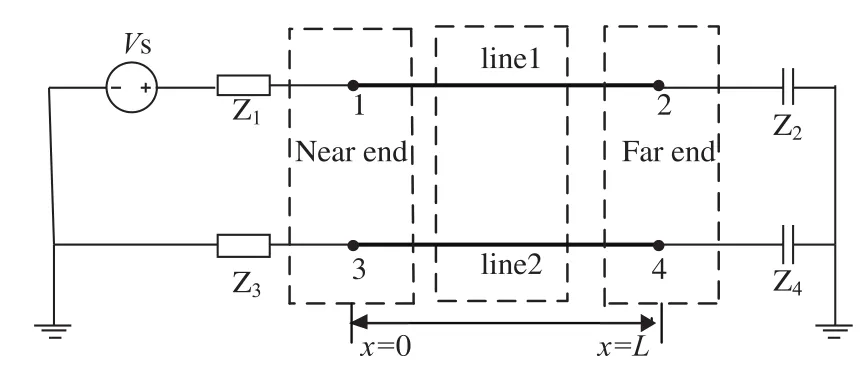
图2 双导体耦合电路模型

图3和图4分别为攻击线远端和受害线两端的电压响应波形。其中，图虚线为文献用传递函数法结合IFFT所得结果，实线为商业仿真软件HSPICE计算出的结果；图为本文方法结合IFFT所得结果。从图中可以看出，本文方法的计算结果和文献及HSPICE软件的仿真结果吻合得很好，从而验证了该方法的有效性。

图3 攻击线远端电压响应波形

图5（a）和（b）分别为受害线近端和攻击线远端电压幅值的频率响应图。从图中可以看出，随着频率的增加，串扰将越来越大，而有用信号的衰减比较大。在高频段出现震荡，主要是由于分布参数系统的传递函数中的纯延迟部分实际上具有无限多的极点造成的。图中所反映的结论与实际中所观察的现象是一致的。

2 多导体传输线串扰的变化规律研究

实际情况下，军用移动电站多使用（3+1）芯多导体电缆为雷达、火炮等装备供电，因此本节我们以（3+1）芯多导体电缆为例来研究串扰的变化规律，更有实际意义。（3+1）芯多导体电缆串扰等效电路模型如图1所示。

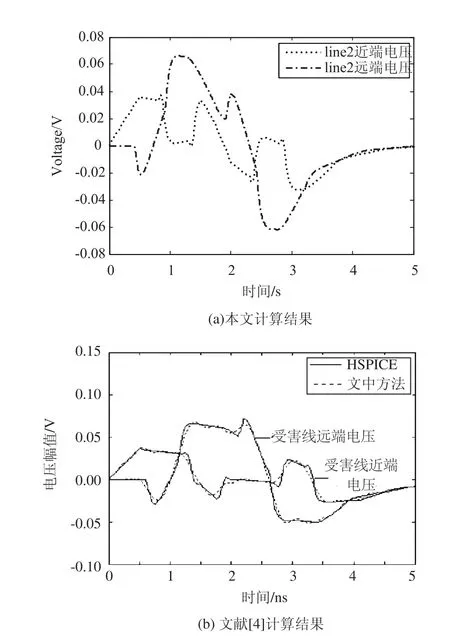
图4 受害线两端电压响应波形

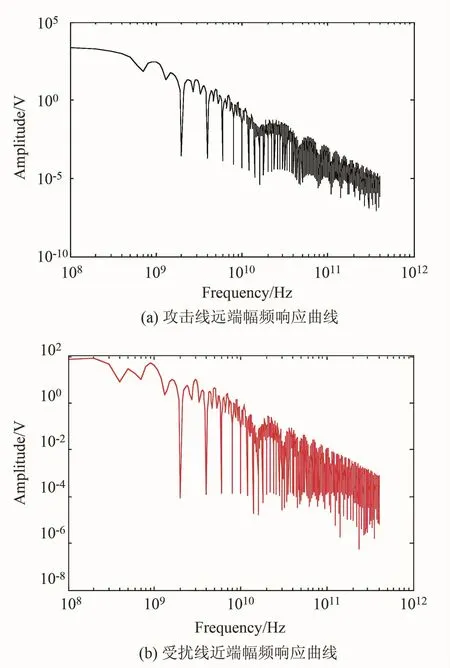
图5 受害线近端和攻击线远端电压幅值频谱

仿真研究对象为一根铺设在地面上的YC型耐压450/750V（3+1）芯无金属屏蔽层重型橡套软电缆，其横截面结构如图6所示。

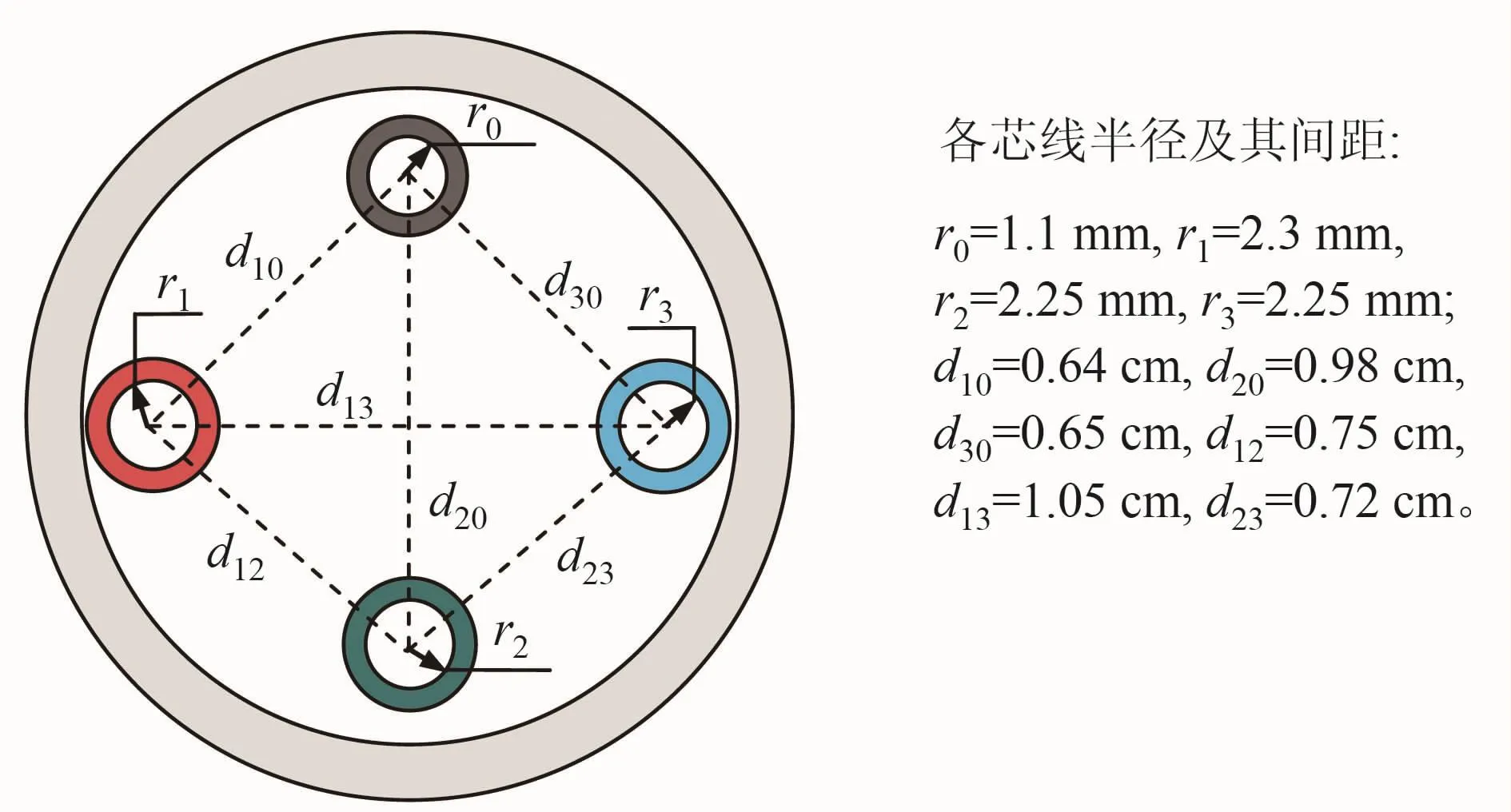
图6 多导体电缆横截面示意图

为了研究电缆本身各种参数对串扰强弱的影响，我们采用数值计算方法[11]来获取电缆的分布参数，电缆分布参数为：

设电缆长度L=10 m，两端端接阻抗为Z1= Z2=Z3=Z4=Z5=Z6=50Ω，干扰源为方波信号，其上升沿与下降沿相等，tr=td=1.5 ns，脉宽p=1 ns。

在下面研究某种参数的影响时，只改变该种参数，其余参数仍恢复到此处的设置。

2.1 干扰源上升、下降时间的影响

图7为当改变干扰源的上升沿和下降沿时间的情况下，计算得到的观测点3感应电压波形。可以看出，随着干扰源波形上升时间和下降时间的延长，受扰线上的感应电压幅值呈减小趋势，且电压波形的上升沿和下降沿时间也会相应延长。

2.2 干扰源脉宽的影响

图8为改变干扰源脉冲宽度的情况下，对应得到的观测点3感应电压波形。可以看出，随着干扰源波形脉宽的变大，受扰线上的感应电压幅值在第一个波峰呈减小趋势，后续波峰呈增大趋势。

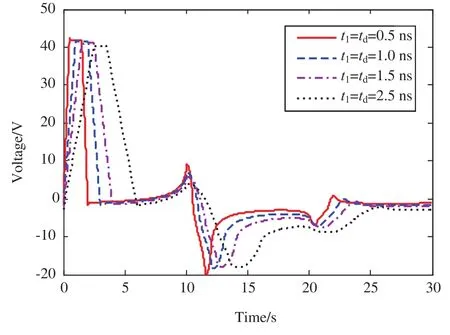
图7 干扰源上升、下降时间影响

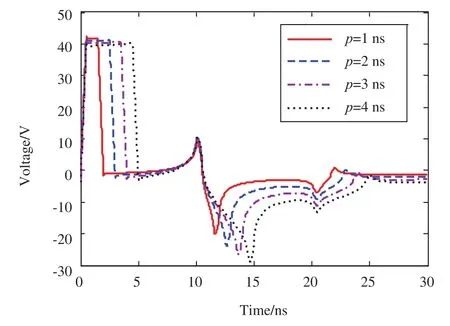
图8 干扰源脉宽的影响

2.3 电缆长度的影响

图9为电缆长度改变时的观测点3感应电压波形。可以看出，随着电缆长度的增加，受扰线上的感应电压幅值呈减小趋势，且波峰的脉冲宽度也逐渐减小，波峰出现时间提前，波峰与波峰之间的时间间隔缩短。

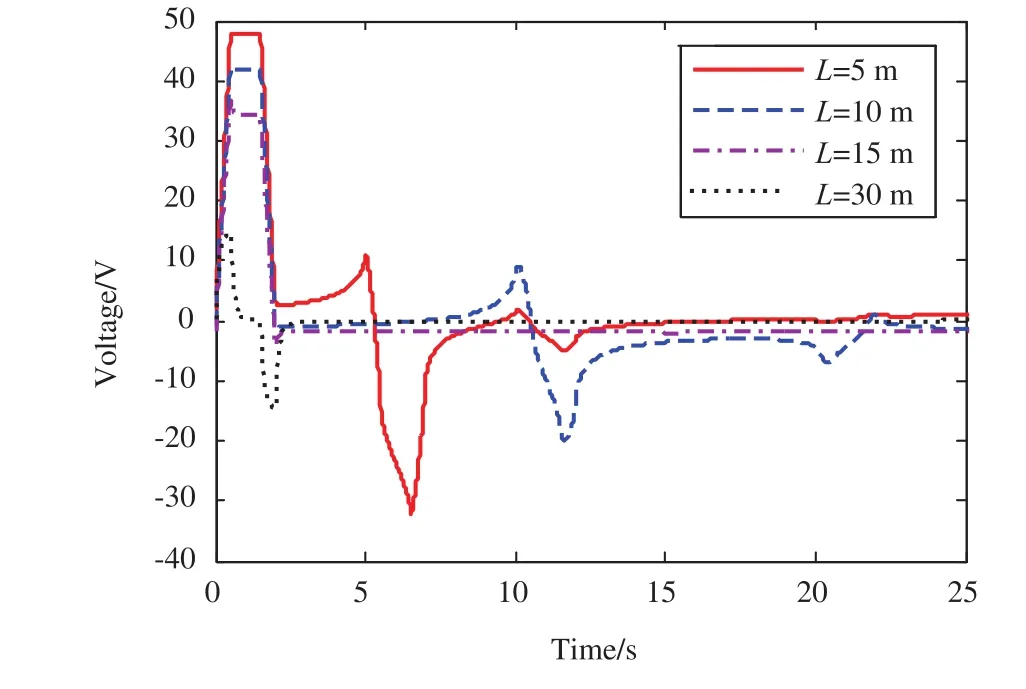
图9 电缆长度的影响

2.4 电缆材料电气参数的影响

图10为当电缆导体电导率变化时，观测点3感应电压波形。分析可见，当导体电导率变化时，受扰线感应电压基本没有变化，这是由于高频时线电阻在传输线特性阻抗中仅占很小的份额，传输线电导率的变化对特性阻抗几乎没有影响。

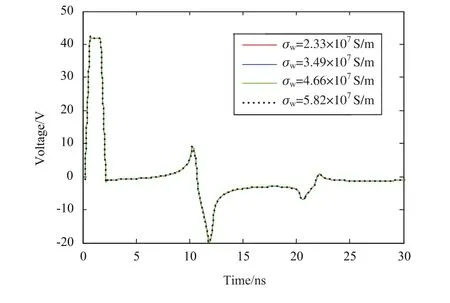
图10 电缆导体电导率的影响

3 结语

基于传输线分布参数节点导纳方程和快速傅里叶逆变换技术，推导了多导体传输线间串扰电压的响应计算公式，仿真分析了其串扰的主要影响因素，有利于提出抑制串扰的合理措施。所用方法计算简便，适于进行多导体传输线缆串扰的研究。

[1] KAMBIZ A，ABDOLALI A.Efficient Method for Timedomain Analysis of Lossy Non-uniform Multiconductor Transmission Line Driven by a Modulated Signal Using FDTD Technique[J].IEEE Transactions on Electromagnetic Compatibility，2012，54（2）：482-494.

[2] 袁正宇.高速芯片内互连系统的电特性分析[D].上海交通大学博士论文，2000.

[3] 李宝忠，何金良，周辉，等.电磁脉冲在传输线上激励电流规律研究[J].信息与电子工程，2010，8（1）：36-40.

[4] 吉小鹏，张启峰，葛龙，等.基于传递函数的高速互连线串扰分析[J].计算机工程，2009，35（12）：283-285.

[5] 焦金龙，王晨，刘源.线缆束电磁兼容仿真技术[J].微波学报，2012，8：57-60.

[6] 张刚，王立欣，刘超.高频多导体串扰的简化三维全波算法及其有效性评估[J].电工技术学报，2012，27（9）：140-145.

[7] 马云双，闻映红，张丹，等.动车组屏蔽线缆间串扰特性及其试验验证研究[J].仪器仪表学报，2013，34（5）：1188-1194.

[8] 秦萌涛，宋文武，王冬冬.舰船舱室中电缆串扰分析[J].电子技术应用，2014，40（3）：75-78.

[9] 唐丽娟，叶志红，陈伶璐.单导体传输线与屏蔽电缆串扰问题的研究[J].科学技术与工程，2013，13（36）：10913-10916.

[10]叶志红，廖成，张敏，等.基于时域BLT的多导体传输线串扰响应分析[J].强激光与粒子束，2014，26（7）：073212-1-073212-4.

[11]C R PAUL.Analysis of Multiconductor Transmission Lines[M].NewYork：Wiley，2007.

Research on the Crosstalk of M ulti-conductor Transm ission Line Based on Distribution Parameter Node Adm ittance M ethod

WANG Chuan-chuan，ZENG Yong-hu，MENG Jie
（State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System，Luoyang 471003，China）

In order to research the crosstalk laws between differentmulti-conductor transmission line's core lines，crosstalk coupling voltage responses are derived based on distribution parameter node admittancemethod and inverse fast Fourier transform technique，then themethod is validated based on an example by comparing the calculation results.Based on the derived equations，the effects of interference source's rising edge time and fall edge time，the pulse width of interference source，the length of cable and thematerial electric parameter of cable are analyzed.The results and conclusions in can be referenced in realizing the response laws ofmulti-conductor transmission lines to electromagnetic pulse and its electromagnetic protection.

distribution parameter node admittance method；multi-conductor transmission line；crosstalk；inverse fast fourier transform

TM246

1673-5692（2015）04-344-06