两栖型指控车非线性横摇安全盆侵蚀研究*

马新谋，潘旭东，于 斌

（1.中北大学，太原 030051；2.山西协城工程招标代理有限公司，太原 030009；3.北方光电集团有限公司，西安 710043）

两栖型指控车非线性横摇安全盆侵蚀研究*

马新谋1，潘旭东2，于 斌3

（1.中北大学，太原 030051；2.山西协城工程招标代理有限公司，太原 030009；3.北方光电集团有限公司，西安 710043）

采用单自由度系统研究了两栖型指控车在规则波激励下的非线性横摇和倾覆，非线性横摇控制方程应用四阶龙格库塔法进行数值积分；以波浪扰动力矩的幅值和波浪的频率作为变量，研究了两栖型指控车的安全盆侵蚀问题。以波浪扰动力矩的幅值为变量的安全盆侵蚀研究结果表明：当波浪扰动力矩大于0.01时，安全盆开始出现侵蚀现象，当波浪扰动力矩大于1.84时，安全盆的安全域已经变成了几个离散的点，随着波浪扰动力矩继续增大，安全盆的安全域将继续严重侵蚀，直到消失为止。以波浪频率为变量的安全盆侵蚀研究结果表明：两栖型指控车的安全盆侵蚀对波浪的频率敏感，安全盆出现明显的侵蚀；随着频率的增大，安全盆侵蚀将不会发生，表明两栖型指控车对高频波浪是安全的。

两栖型指控车，非线性横摇，安全盆侵蚀，非线性动力学，规则波

0 引言

两栖车辆作为武器平台，如果给其安装火炮则称为两栖型自行火炮，再给两栖型自行火炮配装不同配置的火控系统，则变成信息化程度不同的两栖型自行火炮；如果给其安装上指挥控制系统则称为两栖型指控车。两栖型指控车与两栖车辆、船舶一样必须具备两个基本性能，第一是必须能浮在水面上，第二是必须能稳定地浮在水面上。传统的稳定准则靠流体静力学计算出的GZ曲线与坐标轴包围的面积去判断［1］。但是根据这些准则设计出的船舶在受到波浪激励有时会发生倾覆，这种倾覆占船舶事故中相当大的比例［2］。因此，横摇运动是船舶水上运动中最危险的一种，是船舶倾覆的主要原因，已经成为船舶工程领域重要的研究方向之一［3］。船舶力学里采用安全盆(safe basin)理论（安全盆是表征在外载荷作用下船舶经历足够长的时间后不发生倾覆的初始条件的集合）研究船舶的横摇运动特性，研究其倾覆的条件，给出确保安全的安全域。同理，采用安全盆理论也可以研究两栖型指控车的横摇运动特性。

有关船舶安全盆和其他非线性动力学系统安全盆的研究文献较多。Thompson［4-5］最早提出并应用安全盆侵蚀（safe basin erosion）方法研究船舶在规则波浪作用下的倾覆问题；Senjamovic等［6］应用安全盆理论研究了不同形式载荷作用下的船舶倾覆问题和生存概率预报等问题。Long等［7-11］研究了激励幅值、频率、阻尼特性等对安全盆的影响。目前的文献里尚未查到有关两栖车辆、两栖型指控车安全盆侵蚀研究的论文和报告，但是可查阅的文献里马新谋等［12-14］针对两栖车辆的非线性横摇运动进行了较为系统的研究，取得了一些有益的结论。

1 非线性横摇动力学模型

由于研究的两栖型指控车的底盘与文献［14］中的两栖车辆一致，只是一个安装火炮，另一个则安装了指挥控制系统。所以借鉴两栖车辆非线性横摇动力学研究成果，根据某两栖型指控车的总体设计方案，及各信息子系统的布置及其质量、质心分布，给出两栖型指控车的非线性横摇动力学模型为：

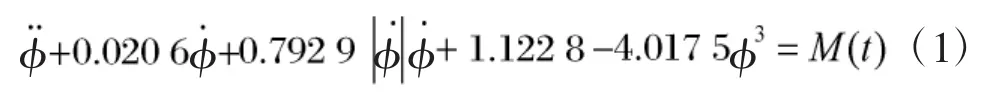
当M（t）=0时，式（1）为静水条件下的非线性横摇动力学方程。如果仅研究静水条件下的力学性能，则不能满足工程需要。在工程实际中肯定存在风浪，常见的波浪载荷存在以下几种情形，规则波的扰动力矩、随机波的扰动力矩和上述两种联合共三种情形。本文仅研究规则波对两栖型指控车的扰动及其安全性影响。规则波浪的扰动力矩的表达式

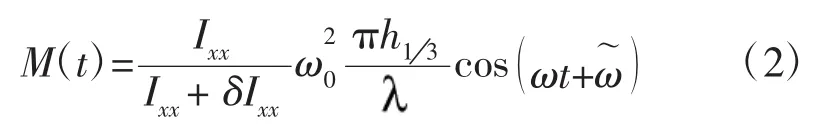
式中：Ixx和δIx分别为两栖型指控车横摇转动惯量和附加横摇转动惯量，单位：kg·m2；ω0为两栖型指控车横摇固有频率，单位：rad/s；为规则波的波长，单位：为规则波的1/3有义波高，单位：m；ω为规则波的频率，单位：rad/s；为规则波的相位，单位：rad。为了理论分析方便，规则波浪扰动力矩可以简化为

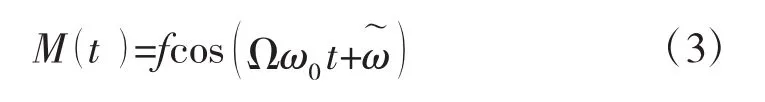
式中：f由海况（水情）和车辆几何特性决定；Ω=ω/ω0为规则波浪频率与横摇固有频率之间的比值。

把式（3）代入式（1）有：

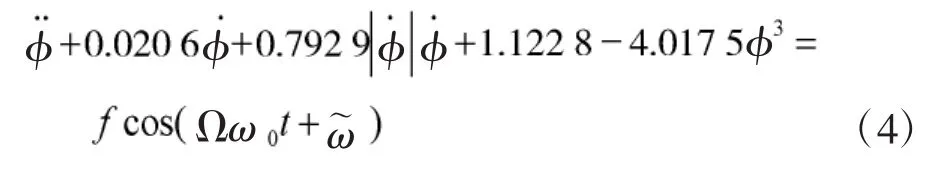
下面就针对式（4）开展两栖型指控车安全盆侵蚀研究，研究两栖型指控车在风浪中航行的安全性。

2 两栖型指控车安全盆侵蚀研究

安全盆侵蚀经常导致工程事故，因此，有必要根据不同的激励幅值和波浪频率扰动下的安全盆的形状，看其是否发生侵蚀，是否安全。安全盆是两栖型指控车非线性横摇动力学方程计算过程中的初始条件为横摇角和横摇角速度组成的相平面。

设第i行第j列的点对应的初值记为：

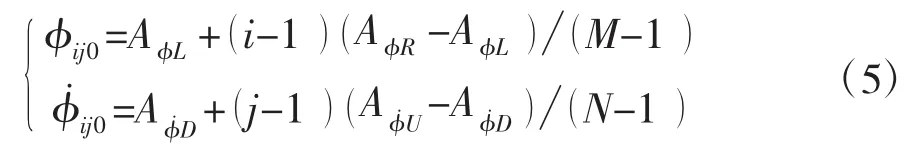
式中：1≤i≤M，1≤j≤N。

计算时间区间为t=0～Tend。如果Tend时的位移和速度还在相平面Asb里，则认为它是安全的，给该点记为“黑色十字”；如果Tend时的位移和速度不在相平面Asb里，则认为它是不安全，将导致倾覆，把该点记为“白色十字”。安全盆侵蚀计算的流程如下页图1所示。

3 波浪扰动力矩的幅值对安全盆的影响

固定波浪频率，考察波浪扰动力矩的幅值对安全盆的影响。计算两栖车辆安全盆侵蚀中采用的相平面 Asb里的参数分别为：AφR=-AφL=1.5 rad，Aφ˙U=-Aφ˙D=2.5 rad/s，M=N=50，Tend=300 s。

在分析计算安全盆时，设波浪的频率为w= 2 rad/s。计算时采用四阶龙格库塔法进行数值积分。当波浪扰动力矩f分别取0.01,0.1,0.5,1.0,1.5,1.8, 1.84时采用图1所示的流程分别计算了相应的安全盆侵蚀。在Pentium4 PC、Windows XP操作系统、内存2 G、128RAM的计算机上计算一个安全盆耗时3小时27分，计算结果如图2所示。

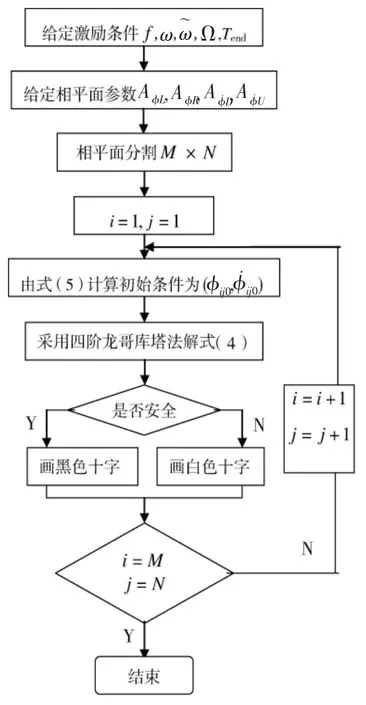
图1 安全盆侵蚀计算流程图

在安全盆里，凡网格上画黑‘+’的区域表明初始条件在这里时安全的，称为安全域；凡网格上空白的区域表明初始条件在这里时是不安全的，称为倾覆域。

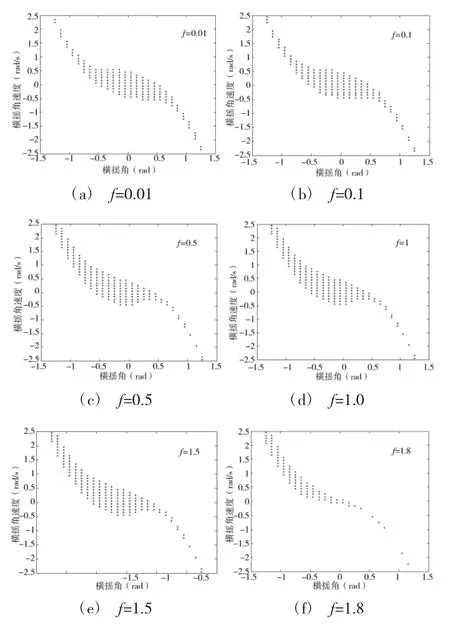
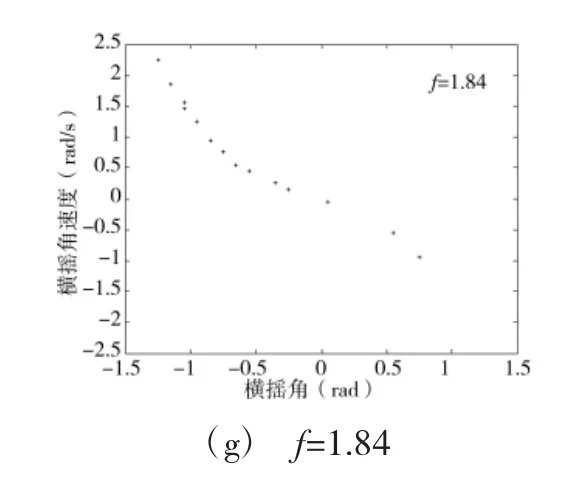
图2 两栖型指控车的安全盆

如图2（a）所示，即当f=0.01时安全盆没有侵蚀，它的边缘是光滑的；当f＞0.01时，如图2（b）～图2（f）所示安全盆将出现安全盆侵蚀，表明随着激励力矩幅值的增加安全盆的安全域越来越小。如图2 (g)所示当f=1.84时，安全盆的安全域几乎消失。

因此，横波的力矩激励幅值f取0.01和1.84为安全盆无侵蚀和安全盆消失的两个阈值。

下面采用这种方法研究不同频率下的两栖型指控车全盆侵蚀问题。

4 波浪频率对安全盆的影响

下面固定波浪力矩幅值，考察波浪频率对安全盆的影响。计算时采用图1所示的流程，分别计算了规则波浪频率与两栖型指控车横摇固有频率之间的比值Ω取不同值的安全盆。计算时Ω分别取0.1，0.2，0.5，0.7，0.8，1.0，1.3，2.0，4.0。Asb里的参数除了M和N取80外，其余同第3节里参数。计算一个图大约需要297 min，计算结果如下页图3所示。

如图3中的9幅图所示，可以看出两栖型指控车的安全盆在规则波激励力矩幅值一定的前提下，随着Ω的变化，两栖型指控车的安全盆的形状发生明显的改变。

（1）随着Ω的增大，安全盆的安全域发生迁移。如图3(a)所示，当波浪的频率为两栖型指控车横摇固有频率的0.1倍时，其安全域主要集中在对称中心和第四象限，第二象限没有安全域。随着Ω的逐渐增大，当Ω=1.0时，即发生共振时，如图3（f）所示其安全域主要集中在对称中心和第二象限，第四象限的安全域越来越小；如果加密计算间隔，可找到使该两栖型指控车安全域在第四象限消失的波浪频率。

（2）随着Ω继续增大，第四象限的安全域又逐渐增大，如图3（g）～图3（i）所示。因此，对于高频的波浪激励而言，该两栖型指控车的安全盆又逐渐增大。因此，两栖型指控车对于高频的波浪激励的安全域相对较大。

5 结论

通过采用数值仿真的方法研究两栖型指控车在规则波浪激励下的安全盆侵蚀问题，可以得出如下结论：

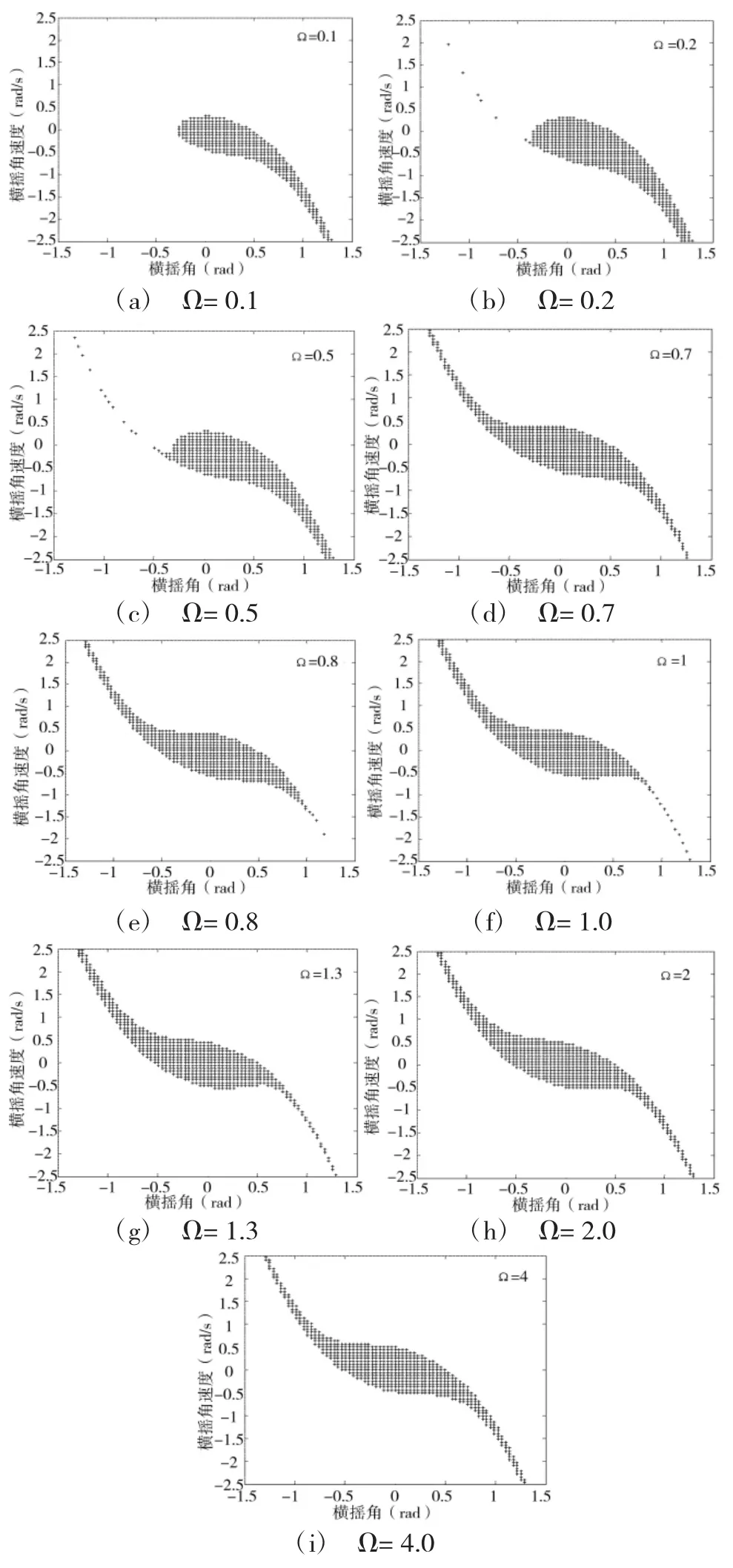
图3 两栖型指控车的安全盆

①两栖型指控车在规则波浪激励下，当波浪的频率固定，激励力矩幅值发生变化，如图2所示，两栖型指控车的安全盆侵蚀显著，安全域随着激励幅值增大越来越小，最后直至消失；②当规则波浪的激励力矩幅值固定，随着波浪频率的增大，如图3所示，两栖型指控车的安全盆侵蚀变化明显。表明两栖型指控车对低频激励的安全域较小，对高频率激励的安全域较大。③以上结论是针对某一特定两栖型指控车的，可能对其他两栖型指控车不适用，但是研究的方法可以通用。采用该方法可针对不同两栖车辆的非线性横摇安全盆侵蚀进行研究，找出其中的规律，为两栖型指控车及两栖车辆的研制工作提供参考。

需要指出的是，上述研究是针对规则波浪条件下的激励力矩幅值和激励频率变化的计算结果。实际的波浪却是随机波浪，因此，要深入研究两栖型指控车的安全盆与激励之间的关系还应研究在随机波浪激励下的安全盆侵蚀问题，这正是我们今后要做的研究工作。

［1］Lewis，E V.Principles of Naval Architecture［M］.Vol.I.Stability and Strength.SNAME.Jersey City.NJ，1988.

［2］Senjanovic I，Parunov J，Cipric G，Safety Analysis of Ship Rolling in Rough Sea［J］.Chaos，Solitons and Fractals，1997（4）：659-680.

［3］Rawson K J，Tupper E C.Basic Ship Theory［M］.5th ed.Butterworth Heinemann，2001.

［4］Thompson J M T.Transient Basins：A New Tool for Designing Ships Against Capsize［C］//Proceedings,IUTAM Symposium on the Dynamics of Marine Vehicles and Structures in Waves. London，UK，1990：325-331.

［5］Thompson J M T，Bishop S R，Leung L M.Fractal Basins and Chaotic Bifurcations Prior to Escape from a Potential Well［J］. Physics Letters A，1987（121）：116-120.

［6］Senjanvic I，Fan Y.Numerical Simulation of a Ship Capsizing in Irregular Waves［J］.Chaos,Solitons&Fractals，1995，5（5）：727-737.

［7］Zhan J L，Seung K L，Joon Y K.Estimation of Survival Proba-Bility for a Ship in Beam Seas using the Safe Basin［J］.Ocean Engng 2010（37）：418-424.

［8］Freitas M S T，Viana R L，Grebogi C，.Erosion of the Safe Basin for the Transversal Oscillations of a Suspension Bridge［J］.Chaos,Solitons and Fractals，2008（18）：829-841.

［9］Wu X，Tao L，Li Y.The Safe Basin Erosion of a Ship in Waves with Single degree of Freedom［C］//Proceedings,15th Australasian Fluid Mechanics Conference,The University of Sydney，Sydney，Australia，2004.

［10］Spyrou K J，Cotton B，Gurd B.Analytical Expressions of Capsize Boundary for a Ship with Roll Bias in Beam Waves［J］.Journal of Ship Research，2002（46）：167-174.

［11］Soliman M S.Fractal Erosion of Basins of Attraction in Coupled Nonlinear Systems［J］.Journal of Sound and Vibration, 1995（182）：727-740.

［12］马新谋，潘玉田，常列珍，等.两栖作战武器非线性横摇动力学研究［J］.火炮发射与控制学报，2010（4）：66-69.

［13］马新谋，潘玉田，常列珍，等.两栖车辆非线性横摇运动的Lyapunov特性指数分析［J］.中北大学学报，2011，32（4）：448-453.

［14］马新谋，潘玉田，常列珍.两栖车辆非线性横摇阻尼系数估计［J］.船舶力学，2013（5）：488-493.

An Investigation on Safe Basin Erosion for Amphibious Command Vehicle Nonlinear Rolling Motion

MA Xin-mou1，PAN Xu-dong2，YU Bin3
（1.North University of China,Taiyuan 030051，China；2.Shanxi Xiecheng Bidding Agency Co.,LTD,Taiyuan 030009，China
3.North Electro-Optics Group Co.,LTD,Xi’an 710043，China）

Nonlinear amphibious command vehicle rolling and capsizing in regular waves is analyzed by a single degree of freedom system.The governing differential equation of motion is integrated by applying the four order Runge-Kutta method.The safe basin in the initial value plane is constructed for different values of the two excitation parameters,which are wave disturbance torque and wave frequency,respectively.It is found that for the wave disturbance torque greater than 0.01,the safe basin erosion occurs,and when the wave disturbance torque is great than 1.84 the safe basin have eroded to some point.And with the wave disturbance torque is further increased,the safe basin erosion is aggravated,until vanished.For the excitation wave frequency,the obtained results indicate that the safe basin is sensitive to the frequency increased,and for high frequency of wave,the safe basin will not erosion,and it is safe for amphibious command vehicle nonlinear rolling motion for high frequency of waves.

amphibious command vehicle，nonlinear rolling motion，safe basin erosion，nonlinear dynamics，regular wave

TJ811+.6

A

1002-0640（2015）07-0143-04

2014-05-15

2014-07-09

军队预研课题；中北大学科学基金资助项目（20130105）

马新谋（1978- ），男，陕西武功人，博士。研究方向：两栖武器水上动力学研究。