断裂点位置对GIS中无拓扑闭曲线简化的影响
2015-06-23高培超谢美慧
高培超,刘 钊,谢美慧,田 琨
(清华大学土木工程系地球空间信息研究所,北京100084)
断裂点位置对GIS中无拓扑闭曲线简化的影响
高培超,刘 钊,谢美慧,田 琨
(清华大学土木工程系地球空间信息研究所,北京100084)
在回顾并总结无拓扑闭曲线简化工作的基础上,分别研究了断裂点位置对地图中人工地物和自然地物简化的影响.采用经典、常用的Douglas-Peucker方法作为简化算法,研究结果表明断裂点位置对人工地物和自然地物的简化结果影响均较大,且在人工地物简化过程中呈现一定的规律性.文章最后给出了断裂点位置选择的具体建议.
断裂点;简化;无拓扑;闭曲线;地理信息系统
数字地球的建设目前已初具成果,并在人类的生活中发挥越来越重要的作用[1-3].矢量数据是地理信息系统[4](Geographical Information System,GIS)中的主要数据类型,其数据量目前正随着数字化工作的推进日益增多并趋向海量.无论从优化存储的角度还是多尺度显示的角度来看,都有必要对矢量数据进行简化.
矢量数据简化主要包括散点抽稀、曲线(包括直线)简化、面简化(主要针对边界线)3种类型,在曲线简化和面简化中,常用的算法有Douglas-Peucker(DP)[5,6]、Opheim[7]、SimpliPoly[8]等,但这些算法均是针对开曲线(Open curve)设计的,而在实际工作中,部分曲线和所有面边界都是首尾相连的闭曲线(Closed curve,又称为多边形).
选择断裂点(Break point)位置,将闭曲线“拆剪”为开曲线,是闭曲线简化工作中的首要任务.对于该问题的处理方法,相关工作可分为3类.
(1)不涉及断裂点问题.
文献[9,10]在简化闭曲线网的过程中,根据闭曲线间的相邻关系提取公共边(已是开曲线),对公共边进行简化,然后再组合为新的闭曲线网.在这种情况下,断裂点位置已被客观确定,无需主动选择.
(2)涉及断裂点问题但未阐明处理细节.
文献[11]在进行形状匹配前简化复杂面状要素,文献[12]对等高线进行简化,文献[13]的简化对象是独立的林权地块边界,文献[14]对二值图像的轮廓进行简化,这些简化对象均为无拓扑闭曲线,采用开曲线算法简化时必须主动选择断裂点位置,但文中均未对断裂方法进行细节阐述.文献[15]提出了一种基于数学特征值对开曲线进行简化的算法,并说明算法可扩展至闭曲线,但未对细节进行深入讨论.
(3)涉及断裂点问题并阐明处理细节.
文献[16]在简化过程中根据等高线与其最大外接矩形的交点,将闭合的等高线划分为左上、上右、右下、下左4段开曲线处理.文献[17]在第二次全国土地调查成果缩编工作中,利用基本农田数据将地类图斑边界分为若干片段,然后采用开曲线简化算法处理.此2项工作通过不同的方法,在无拓扑闭曲线简化过程中均主动选择了断裂点的位置.此外,也有文献采用被动选择(或随机选取)的做法,例如,文献[18]的主要工作是平滑栅格数据的矢量化结果,其在平滑闭合矢量曲线时认为,可以从任一节点处将闭合曲线断裂成开曲线.文献[19]在应对闭曲线简化并选择断裂点时,提出了一种近乎遍历的方法,从而得到产生误差最小的断裂位置.
综上所述,在无拓扑曲线简化过程中,闭曲线的情况存在且不容忽略.闭曲线往往需要断裂成开曲线处理,但对于断裂点位置选择问题的研究相对较少.因此,补充相关研究,了解断裂点位置对简化工作的影响,发现可能存在的规律,并提供合理的位置选择方法具有一定的意义.
1 无拓扑闭曲线的特点
从拓扑学的角度来看,矢量数据结构分为无拓扑矢量数据结构(又称为简单数据结构)和拓扑矢量结构(又称为复杂数据结构).无拓扑矢量数据结构只存储地理实体的位置信息(二维或三维)和属性信息,将地理实体抽象为点、线、面3种基本类型,并不记录地理实体间的拓扑关系.由于部分图形应用中无需基于拓扑关系的空间分析功能[20],且无拓扑矢量数据结构能够更快速地在计算机中显示[21],因此无拓扑矢量数据经常成为空间数据结构的首选.
无拓扑闭曲线作为无拓扑矢量数据的一种,主要特点可总结如下.
(1)以坐标对的形式记录空间对象的位置信息.
(2)由于曲线闭合,因此曲线起点和终点的坐标对相同.
(3)不包含拓扑关系,在表达多边形网状结构时公共边会被相邻的多边形独立存储.
2 简化算法与评价指标
2.1 DP算法
DP算法[5-6]是目前最经典、使用最广泛的一种矢量数据简化算法,由Douglas和Peucker于1973年联合发表,后人在DP算法基础上做了很多优化和改进,使之成为很多简化算法的基础.DP算法的简化流程如下.
(1)确定DP算法中的距离阈值ε.
(2)连接曲线首点和尾点,形成基准线(若首尾点重合,则形成基准点),计算其余各点(即中间点)到基准线的距离.如果所有中间点到基准线的距离都小于ε,则删除所有中间点,否则不删除任何点,但将距离基准线最远的中间点标记为分界点.
(3)分界点将曲线分割成2段,对每段重复执行步骤2,直到每段曲线上的所有中间点到各自基准线的距离均小于阈值ε.
(4)最终仍被保留的点即为简化结果.
2.2 简化质量评价指标
使用定量评价的方法计算由简化操作引起的误差,具体采用的评价指标为长度变形(Length deformation,LD)、矢量偏差(Vector displacement,VD)[22]、面积畸变(Shape distortion,SD)[23],其具体的计算方法分别是:


3 实验
无拓扑闭曲线简化是一项复杂的工作,实际应用中常常需要联合使用多种算法才能的获得令人满意的简化效果[23],但多种算法的存在将使得断裂点位置影响的研究变得参数复杂.考虑到DP算法是目前最经典、使用最广泛的一种矢量数据简化算法,也是当今多种主流算法和最新算法的基础[24-26],本文将采用最基础的DP算法简化GIS无拓扑闭曲线,从而在基础层次探究断裂点位置对简化工作的影响.
由于GIS的处理对象往往是地理空间以及空间中的地物,因此GIS无拓扑闭曲线主要是地物本身或轮廓线.在现实生活中,地物可分为人工地物和自然地物2类.人工地物如居民地、工程建筑物与构筑物、道路等,其特点是比较规则,转弯“急促”,且转角以直角为主;自然地物如湖泊、河流等,广义上的自然地物甚至包括等高线,其特点是线形自然,转弯较为“缓和”,且转角以钝角为主.2类地物的特点不同,因此分2类进行实验.
在实验过程中,分别对仿真数据和真实数据进行测试.仿真数据是理想化、典型化、特殊化地物的代表,使用这样的仿真数据进行实验可以简化冗余参数,方便分析实验结果;真实数据是切实存在于地图中的数据,真实数据比仿真数据复杂,数据特征更为一般化,对真实数据进行实验可以验证仿真实验的结论.
3.1 人工地物
建筑物是人工地物中的典型代表,在一幅地图中,大部分的建筑物轮廓线均较为规则,近似矩形.为方便探究断裂点位置对简化工作的影响,使用矩形仿真数据(如图1).仿真数据中共有12个顶点,其中首顶点和尾顶点重合,坐标值均为(1 000 cm,2 000 cm).所有相邻顶点间隔相同,均为500 cm.5号点和11号点的坐标分别为(3 000 cm,2 000 cm)和(1 000 cm,1 000 cm).为表示曲线的闭合性,在存储矩形仿真数据时,重复储存2次断裂点,使断裂点既成为曲线的起点,又成为曲线的终点.例如,以3号顶点为断裂点的闭曲线中,共存储13个顶点,点号顺序依次是3~12、1~3;又如,以7号顶点为断裂点的闭曲线中,共存储13个顶点,点号顺序依次是7~12、1~7.

图1 矩形仿真数据Fig.1 Simulation data(a rectangle)
考虑到对称性,若以7~12号点为断裂点简化曲线,简化结果将和1~6号点相同.因此仅分别以1~6号点为断裂点,使用DP算法(阈值为500 cm)简化曲线,探究断裂点位置对曲线简化的影响.简化结果如表1所示.

表1 简化效果评价Tab.1 Assessments of the simplified results
分析表1中的数据,可得知当矩形角点(1号点和5号点)作为断裂点时,产生的长度变形、矢量偏差、面积畸变均为零;当断裂点处于2个角点的中点位置时(3号点),产生的误差也为零,但并不绝对(反例为6号点);位置对称的断裂点(2号点和4号点)产生的误差大小相同.但断裂点位置更靠近角点时,误差是否更小,不同断裂点位置产生的误差是否呈线性变化等细节无从得知.
为进一步探究细节,仍使用图1中的矩形,沿边界将其等分为60份,由此获得60个间距相等的顶点,其中相邻顶点间距为100 cm.此时1号点位置不变,其余3个角点的序号依次变更为21、31、51.同样考虑到对称性,只研究1~30号点,将1~30号分别作为断裂点,生成30条闭合曲线,分别使用DP算法(阈值为500 cm)进行简化.在理想情况下,如果同时展示30条闭曲线的化简结果,这些简化后的闭曲线应重合在一起,并与原矩形吻合,但实际效果却如图2所示.

图2 同时展示30条简化结果Fig.2 Displaying all the simplified results at the same time
计算压缩率(剩余顶点数/原始顶点数)、长度变形、矢量偏差、面积畸变,结果如图3所示.
从图3中可以确认上文结果,并综合得出以下结论.
(1)断裂点位置对压缩率的影响较小,在大多数情况下,断裂点位置的改变并不影响闭曲线的压缩率.
(2)断裂点位置对长度变形、矢量偏差、面积畸变的影响很大,并且值得注意的是此3项误差指标的变化曲线相似,峰值点几乎相同.

图3 断裂点位置与简化误差的关系(人工地物)Fig.3 Relationships between the positions of breakpoints and the simplification errors(artificial features)
(3)当以矩形角点作为断裂点时,产生的长度变形、矢量偏差、面积畸变最小(此处为零).
(4)大多数情况下,断裂点位置越靠近角点,产生的简化误差越小,但并不绝对.
(5)将断裂点位置设在两角点连线中点处并不一定能够控制简化误差,例如同样处于中点位置,11号点产生的误差很小,但26号点产生的误差却很大.
(6)随着断裂点位置的顺次改变,简化误差并不呈现线性变化趋势,而是无规律地波动变化.
为进一步验证实验结果,将遥感图像上的2块农作物植被轮廓线作为对象分别进行简化(见图4).与仿真数据不同,这些轮廓线并非标准矩形.每条轮廓线上的顶点个数均大于100,因此数据高度冗余.实验结果表明,当以角点作为断裂点时,产生的长度变形、矢量偏差、面积畸变明显变小(但并非一定最小).实验结果完善了上述第3条结论,并确认了其余结论.
3.2 自然地物
地图上的自然地物包括湖泊边界、河流线、等高线等,自然地物与人工地物最大的区别在于线形较为自然,转弯“缓和”并以钝角(而非直角)为主.本文以我国喀纳斯冰川地区等高线数据①数据来源:中国西部环境与生态科学数据中心(http://westdc.westgis.ac.cn)为例,简化其中的闭合等高线,如图5所示.

图4 农作物植被轮廓线Fig.4 Contours of the land used for crop production

图5 闭合的等高线Fig.5 Closed contours
这里给出图5中最外围等高线的简化评价结果,该条等高线共有91个顶点,全长为6 926.232 8个单位,平均点间距约为770个单位.分别以1~91号点为断裂点,以数值77为阈值,使用DP算法简化等高线.然后依次计算每项简化结果的压缩率、长度变形、矢量偏差和面积畸变.最终计算结果如图6所示.

图6 断裂点位置与简化误差的关系(自然地物)Fig.6 Relationships between the positions of breakpoints and the simplification errors(natural features)
从图6中可以看到,当简化对象为自然地物时,简化误差并未变现出一定的规律性.
(1)随着断裂点位置的改变,闭曲线的压缩率呈上下波动状变化,但浮动范围较小(上下浮动值约为4%).
(2)断裂点位置对长度变形、矢量偏差、面积畸变的影响很大,且影响不同.
(3)当角点(转角较大的点,如18号点)作为断裂点时,产生的长度变形、矢量偏差、面积畸变并未达到最值.
(4)压缩率、长度变形、矢量偏差、面积畸变的变化均不具有规律性,且两两之间并无明显相关性.
为进一步验证实验结果,将我国青海湖的轮廓线作为对象进行简化(图7).该轮廓线上共有560个顶点,具有一定的数据冗余.循环执行简化操作560次,逐次将每个顶点作为断裂点,并计算每次简化后的各项误差指标.实验结果确认了上述结论,当简化对象为自然地物时,简化误差并未变现出一定的规律性.
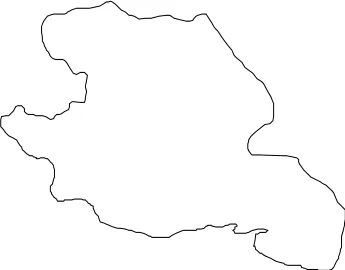
图7 青海湖轮廓线Fig.7 The contour of the Qinghai Lake
4 结论
本文研究表明,在无拓扑闭曲线简化过程中,需要考虑断裂点位置的设置问题.尽管断裂点位置不影响无拓扑闭曲线的形状信息表达,却对简化质量和效果有着不容忽视的影响.本文研究根据属性和几何特征的不同,将待简化对象分为人工地物和自然地物两大类,并以仿真矩形和等高线为典型代表,探究了断裂点位置对2类地物的影响.结论如下.
(1)断裂点位置对简化人工地物和自然地物均有较大影响.
(2)断裂点位置对人工地物的影响具有规律性,当断裂点位置位于角点处时,简化误差较小.
(3)断裂点位置对自然地物的影响具有波动性,但简化误差并没有表现出明显的规律性.
(4)在简化人工地物时,长度变形、矢量误差、面积畸变的变化趋势相关性高,在简化自然地物时变化趋势的相关性低.
(5)在简化工作中,如果待简化对象为城镇地图(含有大量的人工地物),应特别注意断裂点位置的选取规则,建议在编写代码时首选角点.
[1]Goodchild M F,Guo Huadong,Annoni A,et al.Nextgeneration digital earth[J].Proceedings of the National Academy of Sciences,2012,109(28):11088-11094.
[2]Gao Peichao,Liu Zhao,Xie Meihui,et al.The Development of and Prospects for Private Cloud GIS in China[J].Asian Journal of Geoinformatics,2014,14(4):30-38.
[3]郭华东.数字地球:10年发展与前瞻[J].地球科学进展,2009(09):955-962.
[4]刘钊,高培超,闵世平,等.一种大曲率线状实体的三维可视化方法[J].国土资源遥感,2014,26(3):43-47.
[5]费立凡,何津,马晨燕,等.三维Douglas-Peucker算法及其在DEM自动综合中的应用研究[J].测绘学报,2006,35(3):278-284.
[6]Douglas D H,Peucker T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].The Canadian Cartographer,1973,10(2): 112-122.
[7]Mcmaster R B.Automated line generalization[J].Cartographica:The International Journal for Geographic Information and Geovisualization,1987,24(2):74-111.
[8]Chuon C,Guha S,Janecek P,et al.Simplipoly:Curvature-based polygonal curve simplification[J].International Journal of Computational Geometry&Applications,2011,21(4): 417-429.
[9]黄万里,戴文远,余珊.基于面积保持的Douglas-Peucker改进算法的多边形化简[J].科学技术与工程,2009 (24):7325-7328.
[10]禹铭月,王卫安.多边形形状简化及其质量评价[J].测绘与空间地理信息,2011(06):152-155.
[11]付仲良,邵世维.复杂面状矢量要素快速形状匹配方法[J].测绘通报,2011,3(03):26-28.
[12]纪洋,武文波,杨晓伟.等高线自动矢量化的后处理[J].辽宁工程技术大学学报:自然科学版,2008(S1):37-39.
[13]胡芸,方陆明.一种利用拓扑转换消除多边形数据压缩裂缝的方法[J].浙江农林大学学报,2011(04):597-600.
[14]谷柱,武卫,高翌飞,等.X射线安检设备测试图像分割方法[J].无损检测,2009(03):169-172.
[15]Salotti M.Optimal polygonal approximation of digitized curves using the sum of square deviations criterion[J].Pattern Recognition,2002,35(2):435-443.
[16]朱强,武芳,翟仁健.基于通视性原理的等高线化简算法研究[J].中国图象图形学报,2009(02):359-364.
[17]张俊峰,费立凡,黄丽娜,等.第二次全国土地调查成果的多比例尺缩编方法研究[J].测绘科学,2011(02):121 -123.
[18]Yue Jianwei,Wang Jun,Wang Bin.A fast method of smoothing vector graph converted from raster image[J].The International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences,2008,XXXVII(B7):943-945.
[19]Perez J,Vidal E.Optimum polygonal approximation of digitized curves[J].Pattern Recognition Letters,1994,15(8): 743-750.
[20]罗芳,艾廷华,王洪.闭合坐标链多边形数据的拓扑关系快速构建[J].武汉大学学报:信息科学版,2004,29 (6):558-561.
[21]郭嘉亮.基于VxWorks的ECDIS基础显示平台研究[D].哈尔滨:哈尔滨工程大学,2011.
[22]郑春燕,郭庆胜,胡华科.基于蚁群优化算法的线状目标简化模型[J].测绘学报,2011,40(05):635-638.
[23]Park W,Yu K.Hybrid line simplification for cartographic generalization[J].Pattern Recognition Letters,2011,32 (9):1267-1273.
[24]Pallero J.Robust line simplification on the plane[J]. Computers&Geosciences,2013,61:152-159.
[25]Song Xiaomei,Cheng Changxiu,Zhou Chenghu,et al. Gestalt-based douglas-peucker algorithm to keep shape similarity and area consistency of polygons[J].Sensor Letters,2013,11 (6-7):1015-1021.
[26]Gorman G J,Piggott M D,Pain C C.Shoreline approximation for unstructured mesh generation[J].Computers&Geosciences,2007,33(5):666-677.
Effect of Breakpoints Position on Simplification of Closed Curves without Topology
GAO Pei-chao,LIU Zhao,XIE Mei-hui,TIAN Kun
(Institute of Geomatics,Department of Civil Engineering,Tsinghua University,Beijing 100084,China)
This paper reviews the simplification of closed curves without topology,and studies the effects of the position of breakpoints on simplification both in terms of artificial and natural features.The classical Douglas-Peucker algorithm is adopted,and the research result shows that the position of breakpoints can influence both artificial and natural features in the simplification process.Furthermore,there are some influencing rules in the process for artificial features.Specific tips on breakpoints selection are given at the end of the article.
breakpoint;simplification;without topology;closed curve;Geographical Information System(GIS)
P208
A
(责任编辑 苏晓东)
1004-8820(2015)02-0090-06
10.13951/j.cnki.37-1213/n.2015.02.003
2014-08-22
高培超(1991-),男,河南长葛人,硕士研究生.
刘钊(liuz@mail.tsinghua.edu.cn),副教授,主要研究方向为地理信息系统与遥感.
