高超声速风洞颤振试验技术研究

2015-06-22刘子强

实验流体力学 2015年4期

关键词：翼面试验装置动压

季辰, 李锋, 刘子强

(中国航天空气动力技术研究院, 北京 100074)

高超声速风洞颤振试验技术研究

季辰, 李锋, 刘子强*

(中国航天空气动力技术研究院, 北京 100074)

为实现在高超声速风洞中开展颤振试验研究，设计了高超声速风洞颤振试验装置和模型保护机构。风洞试验表明该试验装置可用于开展高超声速风洞颤振试验研究，支撑方式可避免风洞及其他机构对模型的频率干扰；保护机构在高动压情况下可正常工作，达到模型保护效果。试验验证了高超声速风洞固定马赫数阶梯变动压和连续变动压两种风洞开车方式。为验证高超声速风洞颤振试验技术，对平板翼进行了高超风洞颤振试验，试验马赫数为5.0和6.0。试验采用随机子空间法(SSI)辨识结构模态参数，采用Zimmerman-Weissenburger方法预测颤振临界动压，其颤振预测动压比采用活塞理论计算值高12.7%。试验表明目前采用的高超声速风洞颤振试验技术可用于开展高超声速风洞颤振试验研究。

高超声速；风洞颤振试验；亚临界；颤振边界预测；气动弹性

0 引言

高超声速颤振是高超声速飞行器研制中需要解决的重要问题，设计时必须确保飞行器结构在飞行包线内不致发生颤振。高超声速飞行除存在气动加热效应外[1-2]流场特性也非常复杂，存在着激波层、熵层、边界层、复杂波系干扰、激波-粘性干扰以及高温气体效应等复杂流动现象[3]。由于高超声速流动的本质特性为非线性，现有非定常气动力理论不能很好地考虑这些复杂因素的影响，因此在型号设计中还需要通过在高超声速风洞中采用结构动力学相似的模型进行颤振试验研究。

20世纪50、60年代，NASA、美国空军实验室等研究机构建立了高超声速风洞颤振试验技术，开展了大量的高超声速风洞颤振试验[4]，研究了相关设计参数对舵翼面高超声速颤振特性的影响以及一些型号舵翼面的高超声速颤振特性。如Gibson[5]、Morgan[6]、Goetz[7]等人在高超声速氦气风洞中研究了翼型对舵翼面颤振特性的影响；Hanson[8]、Young[9]研究了翼型厚度对舵翼面颤振特性的影响。此外Young[9]还研究了迎角对翼面颤振特性的影响。Rainey[10]、Hanson[8]、Goetz[11-12]、Spain[13]等人研究了超声速、高超声速不同马赫数下舵翼面前缘钝度与其颤振特性的关系。Doggett[14]、Goetz[15]还通过实验研究了考虑翼身干扰效应下的翼面颤振特性。大量的试验数据为其高超声速飞行器设计和高超声速非定常气动力计算和理论的发展奠定了坚实的基础。

国内之前不具备高超声速风洞颤振试验技术，尚未开展过高超声速风洞颤振试验研究[16-17]。笔者提出了在现有高超声速风洞开展颤振试验研究的解决方案，建立了基于中国航天空气动力技术研究院FD-07高超声速风洞的颤振试验装置，通过试验验证了该试验装置以及模型保护技术、固定马赫数变动压技术等。通过固定马赫数阶梯变动压的方式，对类X-15机翼平板翼模型的高超声速颤振特性进行了试验研究，采用Zimmerman-Weissenburger方法[18]对其经典颤振边界进行预估。

1 试验装置和保护机构

1.1 试验装置设计

在常规暂冲式高超声速风洞中开展颤振试验需要解决诸多难题。主要难点如下：

(1) 模型保护问题。暂冲式高超声速风洞启动和关车时存在高于正常开车动压数倍的流场冲击，需要采取措施在风洞启动和关车时保护模型；此外当接近或发生颤振时会有模型破坏的可能，需对模型提供应急保护。

(2) 气动加热影响。国内常规高超风洞常采用加热空气作为流场介质，马赫6.0以上总温较高，模型气动加热明显。因此设计模型和选择测量元件时需考虑并防止气动加热对模型振动特性和测量元件的影响。此外对测量元器件及线路需考虑防隔热问题，对所测的信号需评估可能的热影响和修正。

(3) 试验测量元件及线路保护。高超声速风洞试验动压大，试验中需防止试验测量元件和线路受到流场冲击的影响。尤其对于测量元件和线路外露的模型(如本文采用的实心薄翼模型)，这类问题更为严重。

(4) 风洞开车方式。风洞变动压开车是颤振试验的关键，高超声速试验需要采用固定马赫数变动压风洞开车技术，需要风洞具备一定的动压调节范围。

(5) 振动干扰问题。风洞本体振动噪声和试验段相关部件振动会对弹性模型的振动特性构成干扰，试验机构设计时需尽量避免和减小外部振动环境对模型振动特性的影响。

本文中设计的基于FD-07高超声速风洞的舵翼面颤振试验装置如图1所示。试验机构与保护机构一体设计，模型夹具(Model Clamp)、模型支座(Pedestal)以及保护机构的一部分被支撑挡板(Supporting Baffle)和反射板(Reflective Plate)包围，与流场隔离。模型通过支撑机构安装在平台基座(Platform Base)上，平台基座直接固定在风洞试验段驻室底座上。这种安装形式有效避免了风洞本体振动和其它附加支撑(如插入机构等)的频率对试验模型的干扰。翼面模型位置处于流场锥形均匀区内。保护罩(Spoiler)打开情况下阻塞度为0.1034，满足流场建立要求。试验装置试验能力为模型展长<160mm，弦长<250mm。

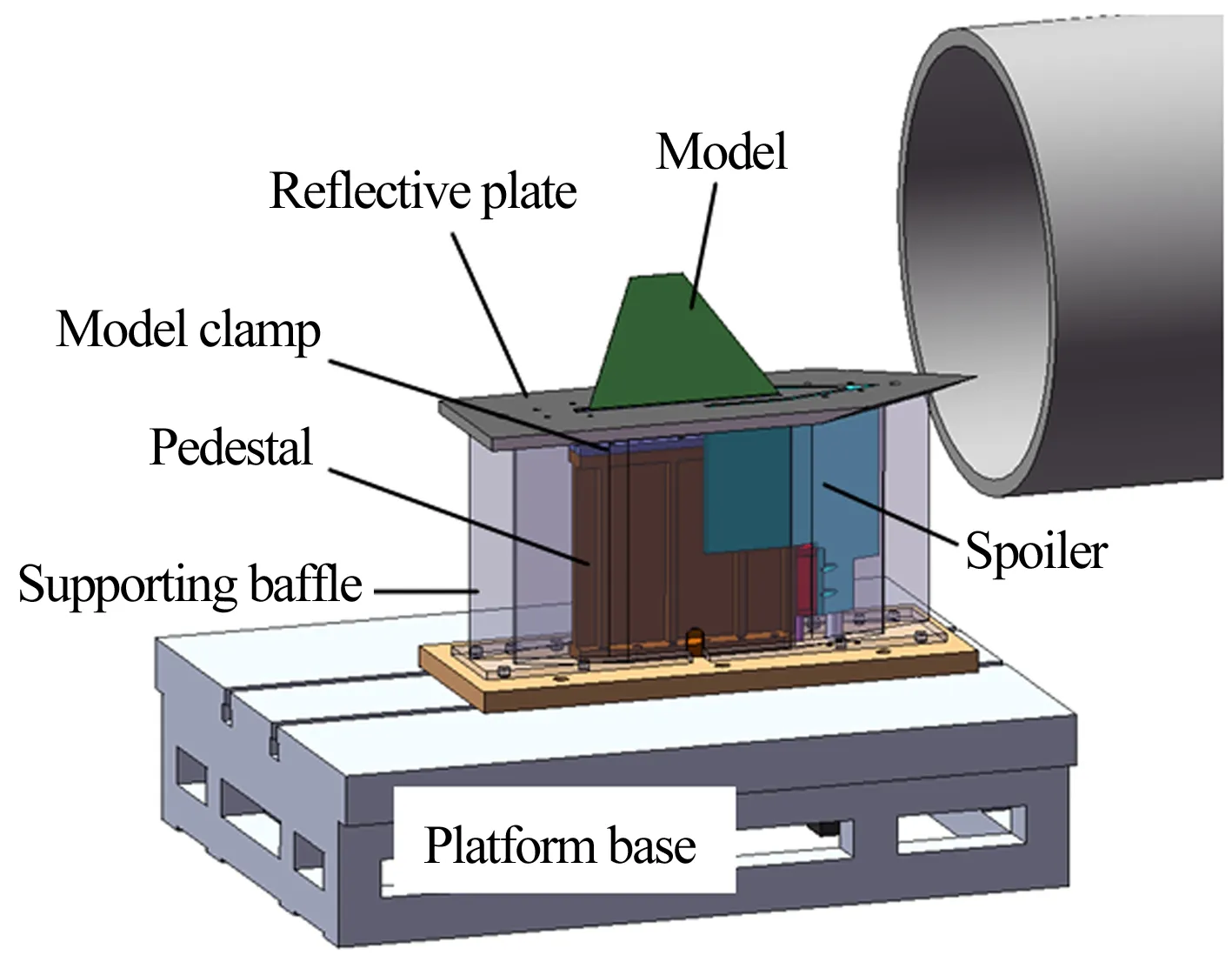
图1 试验装置轴测图Fig.1 Axonometric drawing of the testing apparatus

1.2 保护机构

模型保护采用保护罩保护的方式。如图1所示，保护机构由保护罩、气缸等部分组成。模型需要保护时气缸驱动保护罩弹出，使模型局部流场动压下降；试验时保护罩回撤至与反射板齐平。保护机构控制系统独立于风洞控制系统，并且反应时间短，可以控制在1s以内，可由人工控制或程序控制。

图2为试验时翼面应变信号时域曲线。0～8s保护罩开启，模型处于保护状态；约8s时保护罩回撤，直至23s，模型暴露在流场中处于试验状态；约23s时保护罩弹出，模型处于保护状态。可以看出，保护罩阻止了模型在风洞流场中的大幅振动，起到了模型保护效果。试验过程中保护机构工作正常，能够承受风洞启动和关车高动压气流冲击。

图2 翼面模型应变信号Fig.2 The strain gage signals of wing model

2 风洞及数据测量采集

试验在中国航天空气动力技术研究院FD-07高超声速风洞进行(见图3)。该风洞是一座自由射流暂冲式高超声速风洞。喷管出口直径为Φ0.5m。常用试验马赫数为5～8。本次试验马赫数为5.0和6.0。试验采用位于翼面中下部(见图3)的电阻应变片测量翼面振动信号，两组惠斯通半桥分别测量翼面弯曲和扭转变形。应变片及裸露信号线表面涂覆低模量胶以保护测量元件和信号线免受流场冲击影响。数据采集系统采用Coinv INV3060A数据采集系统，采样频率512Hz。

3 试验模型

试验模型采用类X-15机翼的平板翼，材料为0.47mm均匀等厚钢板。机翼展弦比1.08，根梢比0.273。根部弦长0.2217m，翼尖弦长0.0605m，展长0.1524m。边界条件为根部固支。其前两阶模态振型计算如图4、5所示，模态计算频率和地面振动试

验(GVT)频率如表1所示。采用活塞理论预估(结构阻尼为零)其颤振动压为7.2×104Pa，其颤振形态主要为一阶弯曲和一阶扭转模态的耦合(如图6)。

表1 翼面结构固有频率Table 1 Natural frequencies of the wing model

图3 高超声速风洞中的翼面及颤振试验装置

Fig.3 Wing model and flutter testing apparatus in the hypersonic wind tunnel

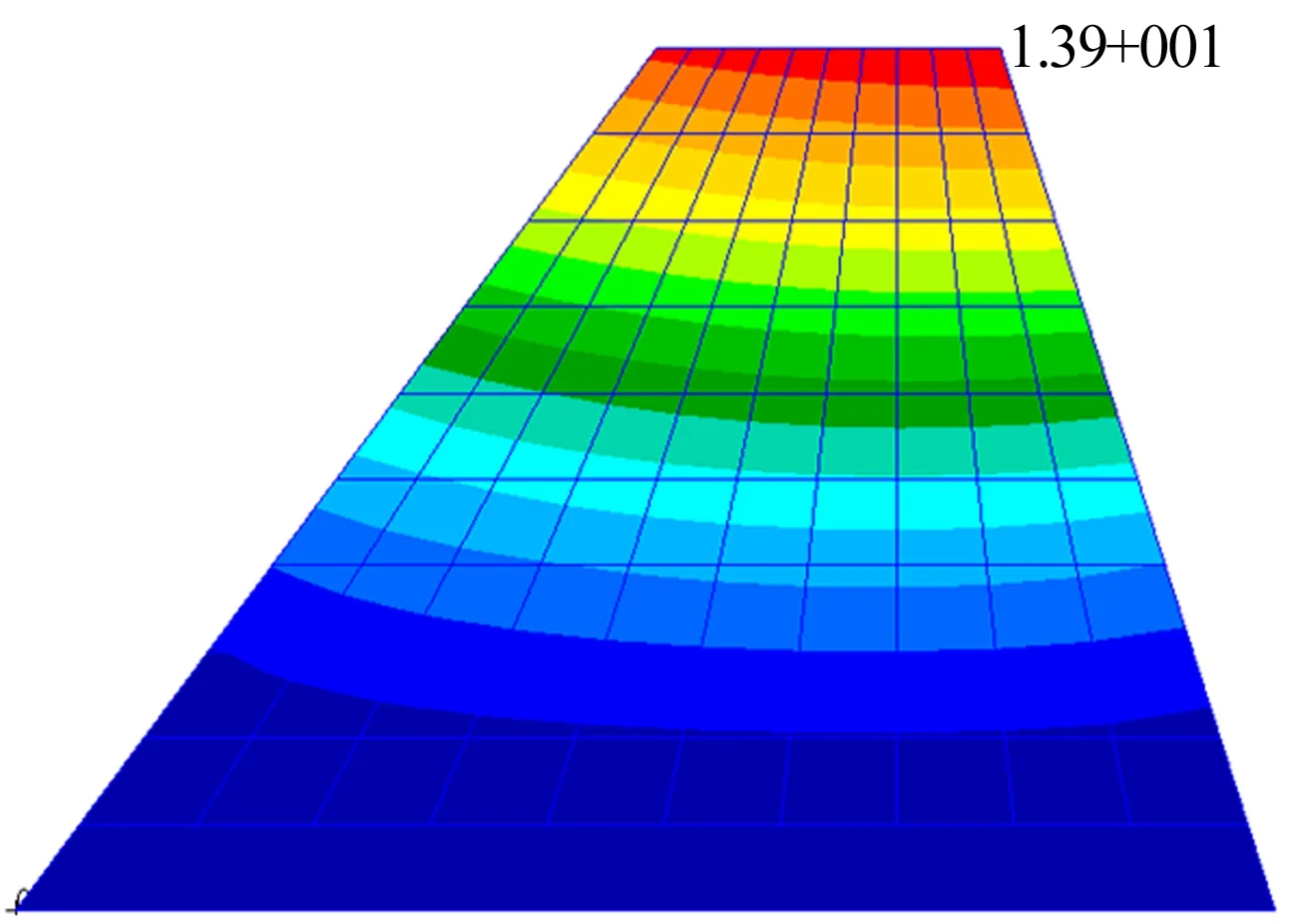
图4 一阶弯曲模态Fig.4 1st bending mode

图5 一阶扭转模态Fig.5 1st torsion mode

图6 颤振动压-频率曲线Fig.6 Flutter q-f plot

4 试验流程和方法

4.1 试验流程

模型及试验装置在风洞试验段安装完成后，在试验前先进行零风速振动试验，采集测量无风情况下模型应变响应数据并辨识其低阶固有频率和阻尼。在每次风洞试验结束后再进行零风速振动试验，以测定试验结束后模型的结构动力学参数，检验模型是否受到破坏。试验采用风洞湍流激励模型。

4.2 风洞开车方式

试验采用固定马赫数变动压的开车方式，即通过增加或降低前室总压实现试验动压的增加或降低。此次试验验证了固定马赫数阶梯增压和固定马赫数连续增压两种变动压方式。阶梯增压每一个动压阶梯稳定时间大于20s。

图7为Ma5.0某车次阶梯变动压开车时动压随时间变化情况，对应动压依次平均为39 535、43 276和46 648Pa；图8为Ma6.0某车次先阶梯变动压(40 041、49 814和56 198Pa)，后连续变动压(56 439～79 535Pa)情况。试验验证了2种开车方式均稳定可控。

图7 Ma5.0阶梯变动压开车情况Fig.7 Results of dynamic pressure control at Ma 5.0

图8 Ma6.0时变动压开车情况Fig.8 Results of dynamic pressure control at Ma 6.0

5 试验结果与分析

5.1 试验情况概述

试验马赫数为5.0和6.0。其中Ma5.0时的试验动压范围为37 705～65 849Pa。

在Ma5.0的试验中随着动压的增加，被测模型的一阶弯曲频率增加、一阶扭转频率降低，同时模型振幅加大，应变响应幅值增加。

在Ma6.0试验时，模型表面应变片在吹风数秒之后便无振动信号输出；考虑到Ma6.0时流场总温将近200℃，同时结合翼面红外热像监测结果分析其原因可能是应变片高温失效导致。试验没能得到该马赫数下的有效试验数据。

5.2 模态参数辨识

采用功率谱计算初步分析模型振动频率。图9为零风速试验翼面应变响应的曲线，图10为该响应数据的功率谱。结合GVT试验情况可辨识出该翼面模型风洞安装状态的一阶弯曲频率为25.4Hz，一阶扭转频率为73.4Hz，与地面GVT试验结果(见表1)基本一致。

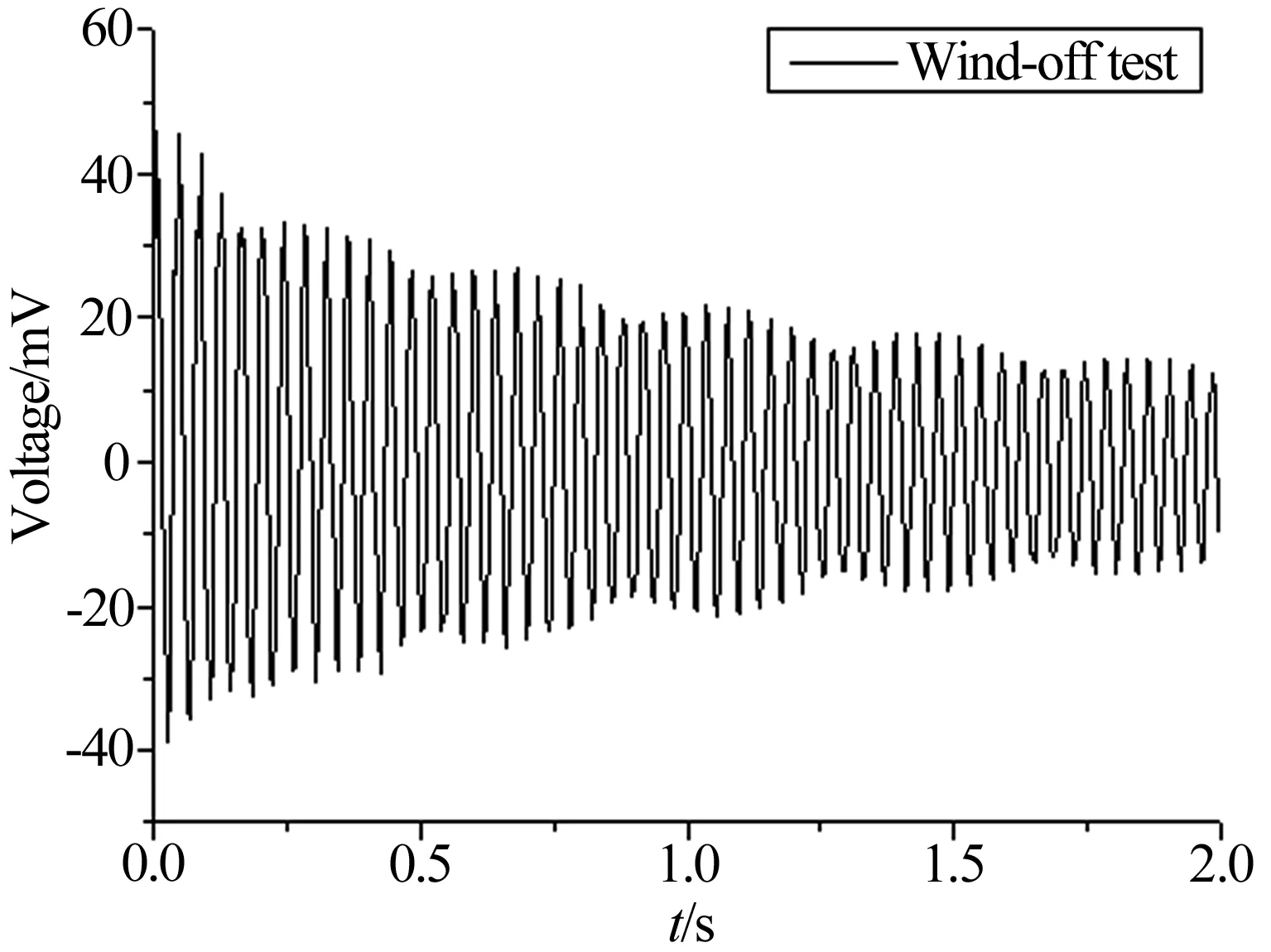
图9 零风速试验翼面应变响应信号Fig.9 Response signals of wing model in wind-off test

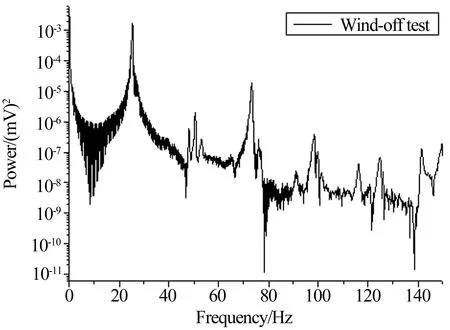
图10 零风速试验响应功率谱Fig.10 Power spectrum of response in wind-off test

图11为风洞试验状态(Ma5.0，动压50 374Pa)下翼面应变响应曲线，图12为该响应数据功率谱。结合图10和12可以看出，风洞试验中模型一阶弯曲频率和一阶扭转频率发生耦合。

采用随机子空间法(SSI)识别试验模态参数。图13为所辨识的阻尼和频率随动压的变化情况。图中可以看出随着动压增加，模型一阶弯曲频率增加，一阶扭转频率下降。一阶弯曲和一阶扭转的阻尼随动压增加基本呈现下降趋势。

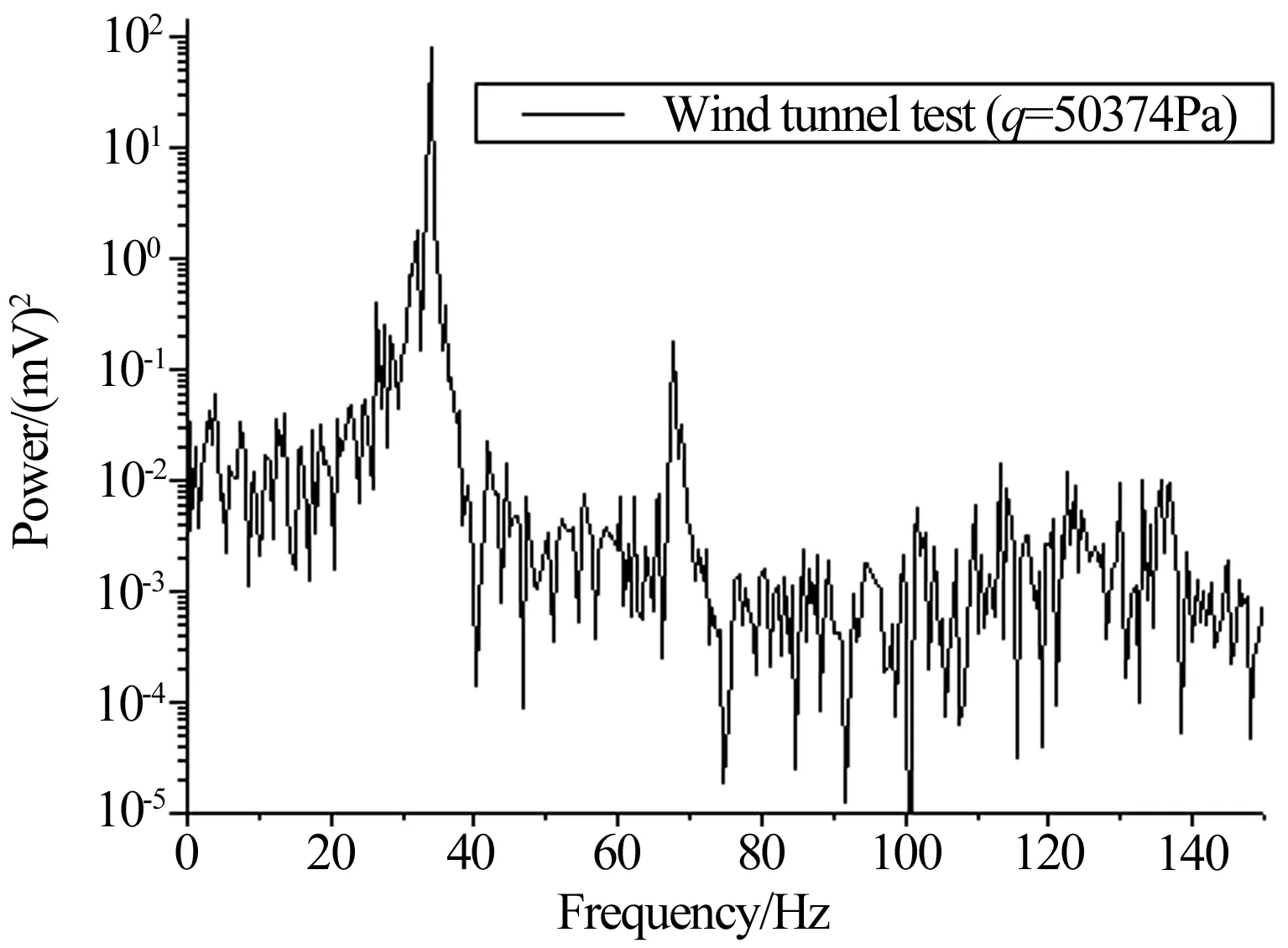
图12 风洞试验翼面响应功率谱Fig.12 Power spectrum of response in wind tunnel test

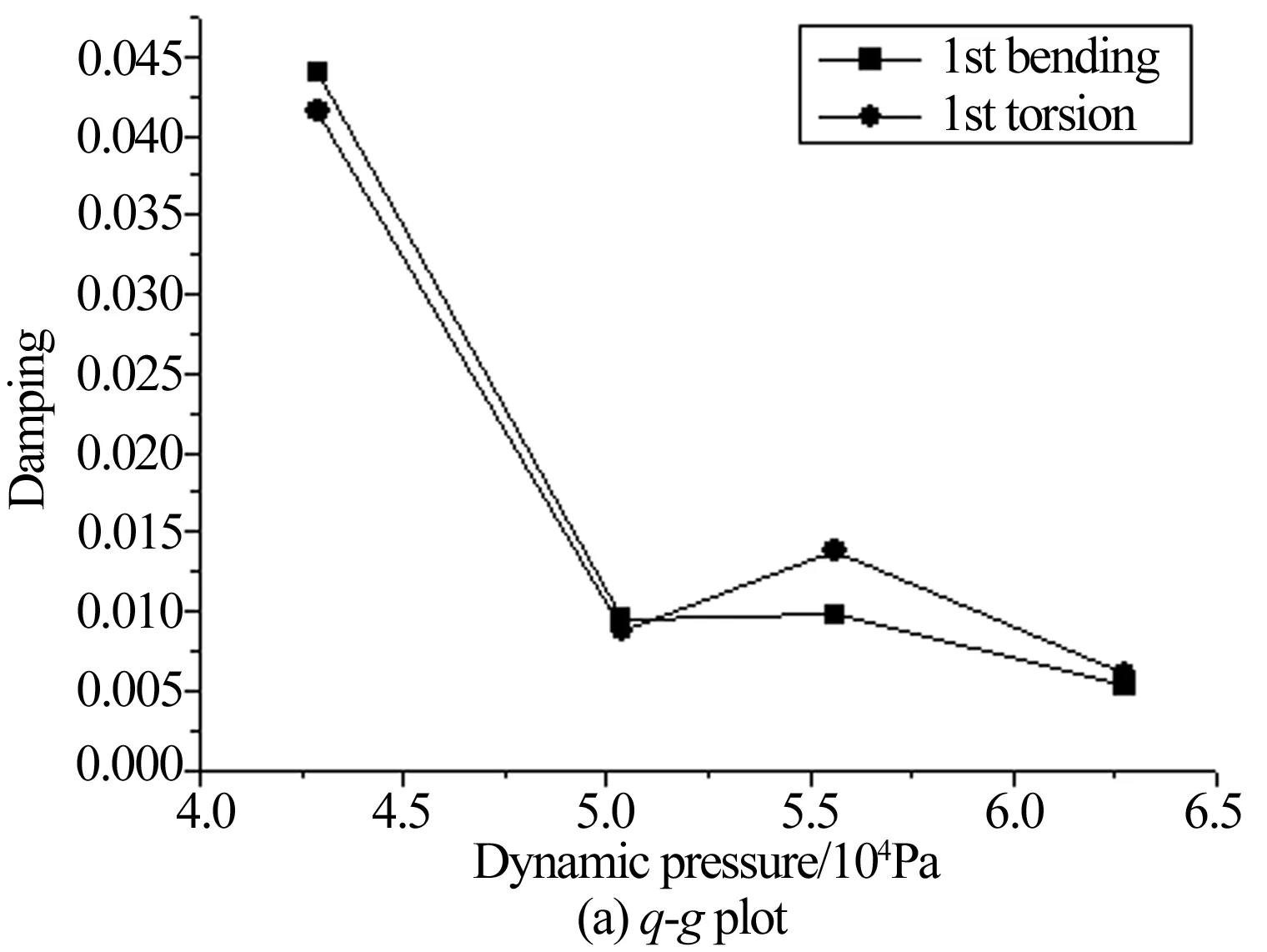
图13 典型试验验动压模态参数辨识结果

Fig.13 Identification of modal parameters at typical testing dynamic pressure

5.3 亚临界颤振预测

采用Zimmerman-Weissenburger方法[18]进行颤振边界预测。该方法通过构造颤振边界函数，并通过对颤振边界函数随动压的变化进行外插判断颤振临界动压，适用于经典颤振的预测。

颤振边界函数F为与颤振相关的模态频率ω和模态阻尼β的函数。

各动压点下的颤振边界函数值计算如图14所示，通过二次多项式外插得到颤振边界函数为零的经典颤振临界点动压为8.25×104Pa。其值比采用活塞理论计算(结构阻尼为零)的颤振动压(7.2×104Pa)高12.7%。

图14 亚临界颤振预测Fig.14 Subcritical prediction of flutter parameter

该组亚临界外推试验数据中的最大试验动压为62 766Pa，距离预测的颤振动压相差约23.9%。为获得更为精确的颤振预测动压需要进一步提高试验动压来逐步逼近颤振临界点。但对于本文所研究的平板均厚薄翼模型，试验中发现其在动压较高的情况下会发生较大侧向变形，这种大变形引起的结构非线性、结构预应力甚至局部支撑状态改变等因素会使得试验中模型结构动力学特性发生改变，这种结构变化要先于经典颤振的发生，因而较难采用直接观测法测量平板翼的经典颤振边界。

6 结论

(1) 采用本文设计的颤振试验装置成功完成高超声速风洞颤振试验研究。该试验装置能够有效避免风洞本体振动以及其它部件对模型自身频率的干扰。保护罩形式的保护机构能够经受风洞启动和关车动压的冲击，在流场中有效地保护模型。

(2) 对平板翼模型进行高超声速亚临界颤振试验，采用颤振边界函数法预测其经典颤振边界，结果表明该模型的经典颤振临界动压比活塞理论计算值高12.7%。

(3) FD-07高超风洞的变动压开车方式和动压变化梯度可以满足高超声速风洞颤振试验要求。Ma6.0以上高超声速颤振模型设计时需采取措施防止气动加热对信号采集以及模型结构动力学特性的影响。

(4) 对于等厚平板薄翼模型在高超声速经典颤振发生前会由于振幅或载荷过大发生结构动力学特性的变化，因而较难采用直接观测法得到平板薄翼的经典颤振边界。

[1] Garrick I E, Cunningham H J. Problems and developments in aerothermoelasticity[C]//Proceeding of Symposium on Aerothermoelasticity. ASD-TR-61-645, 1962.

[2] Doggett, Robert V, Jr. An observation on the pictorial representation of aeroservothermoelasticity[R]. NASA-TM-104058, 1991.

[3] 李素循. 典型外形高超声速流动特性[M]. 北京: 国防工业出版社, 2007.

Li Suxun. Hypersonic flow characteristics of typical configuration[M]. Beijing: National Defence Industry Press, 2007.

[4] Terry M Harris. Aeroelasticity research at wright-patterson air force base (wright field) from 1953-1993[J]. Journal of Aircraft, 2003, 40(5): 813-819.

[5] Frederick W Gibson. Flutter investigation of models having the planform of the north american X-15 airplane wing over a range of Mach number from 0.56 to 7.3[R]. NASA-TM-X-460, 1961.

[6] Homer G Morgan, et al. Flutter tests of some simple models at a Mach number of 7.2 in helium flow[R]. NASA MEMO 4-8-59L,1959.

[7] Robert C Goetz, et al. Hypersonic flutter analysis using measured static aerodynamic derivatives, and comparison with experiment[R]. NASA-TN-D-5233, 1969.

[8]Perry W Hanson. Aerodynamic effects of some configuration variables on the aeroelastic characteristics of lifting surfaces at Mach numbers from 0.7 to 6.86[R]. NASA-TN-D-984,1961.

[9] Lou S Young, et al. Effects of angle of attack and thickness ratio on the flutter of a rigid unswept diamond-airfoil-section wing at a mach number of 10.0[R]. NASA-TN-D-1380, 1962.

[10] A Gerald Rainey, et al. Aeroelastic research at high speeds[R]. NASA-TM-X-326, 1960.

[11] Robert C Goetz, et al. Effects of leading-edge bluntness on flutter characteristics of some square-planform double-wedge airfoils at a mach number of 15.4[R]. NASA-TN-D-1487, 1962.

[12] Robert C Goetz, et al. Effects of leading-edge sweep on flutter characteristics of some delta-planform surfaces at a Mach number of 15.4[R]. NASA-TN-D-2360, 1964.

[13] Charles V Spain, et al. A flutter investigation of all-moveable NASP-LIKE wings at hypersonic speeds[R]. AIAA-93-1315, 1993.

[14] Robert V Doggett Jr. Experimental flutter investigation of some simple models of a boost-glide-vehicle wing at Mach numbers of 3.0 and 7.3[R]. NASA-TM-X-37, 1959.

[15] Robert C Goetz. Experimental flutter study of a wing-fuselage configuration at a Mach number of 15.4 and comparison with theory[R]. NASA-TN-D-3046, 1965.

[16] 季辰, 冉景洪, 刘子强. 亚跨风洞中舵面亚临界颤振试验[J]. 实验流体力学, 2011, 25(3): 37-40.

Ji Chen, Ran Jinghong, Liu Ziqiang. Flutter test of rudder in sub-tran-supersonic wind tunnel using subcritical response methods[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3):37-40.

[17] 郭洪涛, 路波, 余立, 等. 某战斗机高速全模颤振风洞试验研究[J]. 航空学报, 2012, 33(10): 1765-1771.

Guo Hongtao, Lu Bo, Yu Li, et al. Investigation on full-model flutter of a certain fighter plane in high-speed wind tunnel test[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10):1765-1771.

[18] Zimmerman N H, Weissenburger J T. Prediction of flutter onset speed based on flight testing at subcritical speeds[J]. Journal of Aircraft, 1964, 1(4): 190-202.

(编辑：张巧芸)

Research on flutter test technique in hypersonic wind tunnel

Ji Chen, Li Feng, Liu Ziqiang*

(China Academy of Aerospace Aerodynamics, Beijing 100074, China)

In order to conduct flutter test research in hypersonic wind tunnels, a hypersonic wind tunnel flutter test apparatus and a model protection device in the form of protective cover were designed. Wind tunnel tests show that the apparatus can be used to carry out the hypersonic wind tunnel flutter test research and to prevent the test model from being interfered by the wind tunnel vibration. The protection device can work in high dynamic pressure situations and protect the model effectively. The results also validate the two ways of driving the wind tunnel with the dynamic pressure changing step by step or continuously at a fixed Mach number. In order to verify the hypersonic wind tunnel flutter testing technique, flat wings flutter tests were conducted on in the hypersonic wind tunnel at Mach 5.0 and 6.0. The stochastic subspace method was used to identify structural model parameters, and the Zimmerman-Weissenburger method was used for predicting the critical flutter dynamic pressure. The results of this prediction were 12.7% larger than the calculated values using the piston theory.

hypersonic;wind tunnel flutter test;subcritical;flutter boundary prediction;aeroelasticity

1672-9897(2015)04-0075-06

10.11729/syltlx20150005

2015-01-14;

2015-02-04

国家自然科学基金(91216202)；国防基础科研题目(B0320110011)

JiC,LiF,LiuZQ.Researchonfluttertesttechniqueinhypersonicwindtunnel.JournalofExperimentsinFluidMechanics, 2015, 29(4): 75-80. 季辰, 李锋, 刘子强. 高超声速风洞颤振试验技术研究. 实验流体力学, 2015, 29(4): 75-80.

V215.3