纹影定量化在火焰温度测量中的应用

2015-06-22杨臧健王明晓沈忠良钟英杰

实验流体力学 2015年4期

关键词：光度法折射率镜片

孟晟, 杨臧健, 王明晓, 沈忠良, 邓凯, 钟英杰

(浙江工业大学能源与动力工程研究所, 杭州 310014)

纹影定量化在火焰温度测量中的应用

孟晟, 杨臧健, 王明晓, 沈忠良, 邓凯, 钟英杰*

(浙江工业大学能源与动力工程研究所, 杭州 310014)

基于传统“Z”字形纹影系统，采用标准光度法对火焰温度进行了定量化。标准光度法通过一个标定镜片来建立火焰纹影图像的灰度值和光线偏转角之间的定量关系，并利用轴对称假设建立光线偏转角和折射率之间的关系。最后通过盖斯定律和理想气体方程得到火焰温度。对其中涉及到的反演算法进行了比较，结果显示直接积分法和Abel逆变换法误差最小，Radon逆变换受滤波函数影响较大，而迭代重建法在离散点数量较少的情况下误差最大。将纹影定量化所得到的温度曲线和热电偶所测结果值比较，证明了标准光度法对纹影火焰定量化的有效性。

纹影定量化；温度测量；标准光度法；Abel逆变换；Radon逆变换；迭代重建法

0 引言

纹影技术作为非接触式流场可视化手段已存在近百年，广泛应用于射流、空气动力学和传热等研究领域。然而在实际应用中，纹影通常仅作定性观察和分析，极少作为定量化的测试手段。这主要有2个原因：首先，影响纹影图像灰度的因素很多，如光源强度、玻璃透射率、测试区厚度等，导致难以建立图像与待测物理量之间的定量关系；其次，纹影图像反映折射率的一阶导数场，提取数据困难。然而，随着计算机技术，特别是图像处理技术的发展，纹影的定量化测量逐渐成为了可能。

国外，Agrawal等[1]利用彩色纹影得到了火焰的温度场。Hargather 等[2]对“Z”字形纹影、彩色纹影和背景纹影(BOS)在平板传热实验中的定量化进行了比较，结果显示3种纹影技术在平板传热试验中都可以达到很好的精度。国内，叶继飞等[3]利用彩色纹影对密度场进行了定量化测量。周昊[4]等采用背景纹影对火焰温度进行了定量化测量。

本文采用“Z”字形纹影进行火焰温度场定量化测量，主要解决2个问题：(1)纹影图像中偏转角的定量问题；(2)由偏转角反演温度分布。偏转角定量最直接的定量化方法是绝对光度法。通过确定图像上光线明暗的绝对值，来获得光线的绝对偏转角。这种方法除了要知道纹影系统几何尺寸外还需要知道绝对光源强度等，因此对系统设置的准确性要求较高。另一种是标准光度法，其降低了对纹影系统设置的要求，将这些系统信息通过标定镜片来表达，减少了误差来源。采用标准光度法来进行纹影定量化的相关研究较少。因此，本文开展了该方法的研究工作。

温度场反演的关键是利用图像断层假设，采用反演算法由偏转角获得折射率场。简单火焰可以认为在时间平均下是轴对称的[5]。非轴对称的三维定量化需要利用Radon逆变换[6-7]，基于轴对称假设的定量化需要利用Abel逆变换[8-10]。但是不同的算法，可能导致的误差是不一样的，需要深入研究。

本文利用高斯函数产生假想的偏转角分布，通过模拟实验比较了不同反演算法的特性。基于轴对称假设，采用标准光度法对本生型甲烷火焰的温度进行了定量化，并与细丝热电偶的测温结果进行了比较。

1 原理和算法比较

纹影图像反映的是光线经过一个折射率变化的流场后的偏转。偏转角θ和折射率n的关系为:

(1)

其中，x方向为光线入射方向，如图1所示。

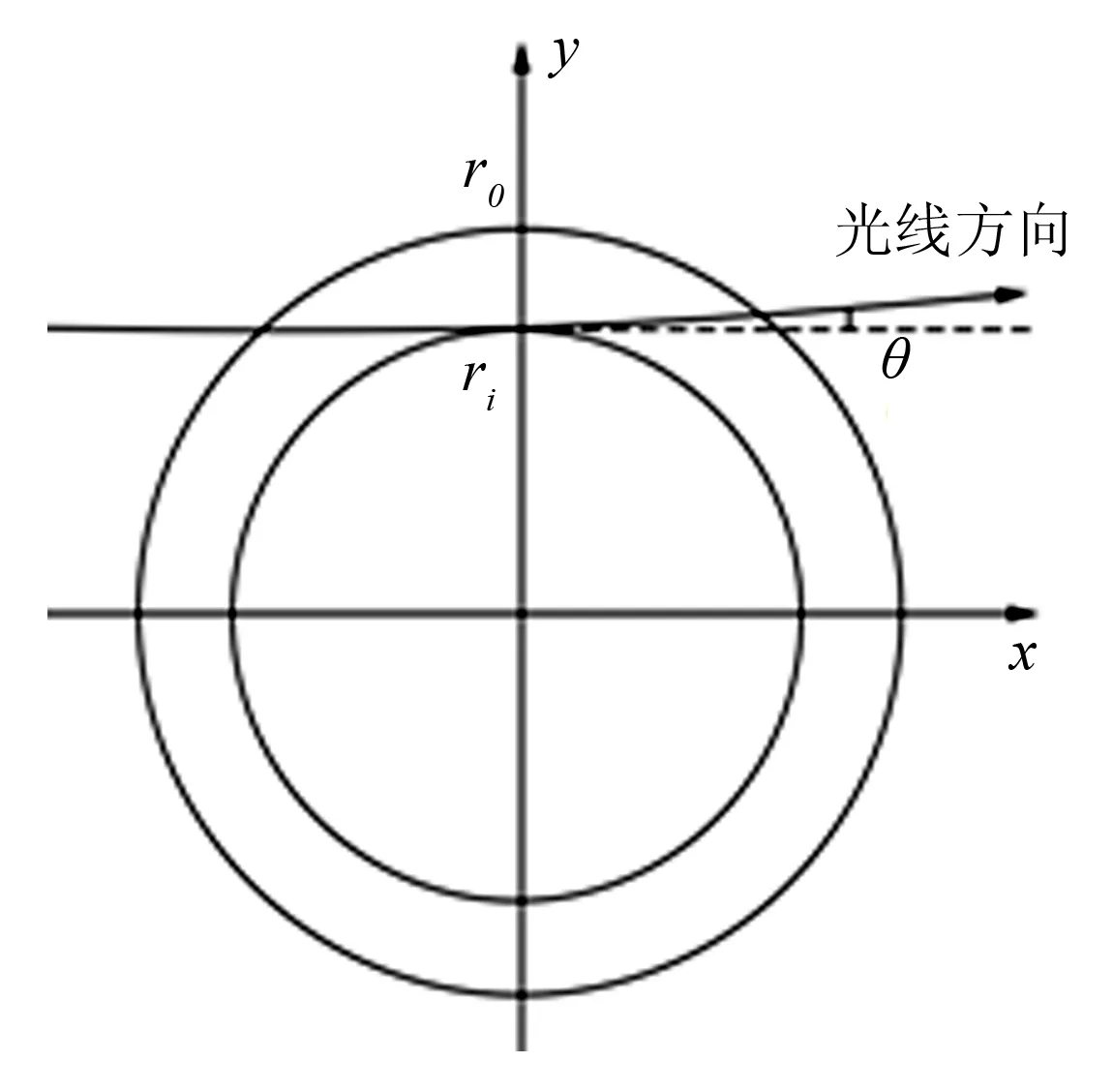
图1 光线经过流场截面后偏转示意图Fig.1 Light deflection through a flow field

但是图像信息主要是灰度、色彩等，并不直接反应偏转角θ，还需要将这些信息加工处理。“Z”字形纹影可以通过标定镜片建立起图像上灰度和偏转角θ的关系，标定镜片的作用将在实验设置部分详细介绍。彩色纹影通过加装彩色滤片建立起图像上色调(hue值)和偏转角θ的关系。背景纹影则通过计算图像像素偏移量来获得偏转角θ。

在获得偏转角θ后，可以通过积分变换建立起偏转角θ和折射率n的关系。假设火焰是轴对称的，那么(1)式就可以改写成：

(2)

式中：rn指火焰截面最外圈半径，ri指θi所对应的半径,y等于ri，C是折射率n的函数。

折射率n和密度ρ可以通过Gladstone-Dale关系式[2]得到：

(3)

式中：κ为Gladstone-Dale常数，它的值和气体组分以及波长有关，文中取κ为定值。

而密度ρ和温度T之间的关系通过理想气体方程建立。当压力近似不变时，温度T和折射率n有如下关系：

(4)

式中：n0是指在参考温度T0下的折射率，也就是环境中空气的温度和折射率，n0取1.00029，T0取300K。

在公式(1)～(4)中，(2)式中通过偏转角θ来得到折射率n是关键。常见的算法有直接积分法，Abel逆变换，Radon逆变换和迭代重建法。

1.1 直接积分法

假设在半径ri和半径ri+1之间，折射率成线性变化。从而折射率梯度可以表达为：

(5)

利用(2)式，对于每一个(ri,ri+1)区间分段直接积分得到：

(6)

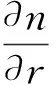
1.2Abel逆变换

从(2)式出发，得到其Abel逆变换方程如下：

(7)

文献[11]中认为在区间(ri,ri+1)内偏转角θ呈线性变化能获得最高的积分精度。由(7)式可得：

(8)

式中：θj已知，对于每一个n(ri)，y是一个常数，等于ri。同样，计算从最外层半径r0开始，逐步分段积分到ri。

1.3 Radon逆变换

实际上，Abel逆变换是Radon逆变换的特殊情况[12-13]，对于二维轴对称情况二者等价。对于平面上的可积函数f(x,y)，沿直线Lθ,r:xcosθ+ysinθ=r积分可得其Radon变换：

(9)

式中，对于纹影而言f(x,y)指折射率分布n(r)。其逆变换公式为：

(10)

式中，通常投影区间在(0,π)之间，因为(π,2π)的投影结果和其一样。

1.4 迭代重建法

由图像断层技术可知，M条平行光线形成的总的射线投影为：

(11)

式中，对于p×p的图像矩阵，N=p×p。对于纹影而言，θM即第M条射线所产生的偏折角。由于纹影入射光线互相平行，这M条射线所形成的M个超平面互相正交。因此虽然M≪N，但此方程组有唯一解。

图2 迭代算法网格示意图Fig.2 Iteration algorithm grid

图2中，假设流场切面的半径为10个像素，N=10×10。根据文献[4]的方法，半径r=9.5像素处的偏转角为：

(12)

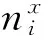
(13)

由于(13)式中的系数矩阵是下三角阵，因此迭代一次便可得到ni的值。

1.5 算法比较

为了比较上面分析的不同重建法，假设流场截面的折射率分布符合理想的高斯函数：

(14)

然后通过文献[14]的方法，对式(14) 积分得到假想的偏转角分布，如图3所示。然后利用假想的偏转角通过不同算法反演得到折射率(函数幅值)分布。

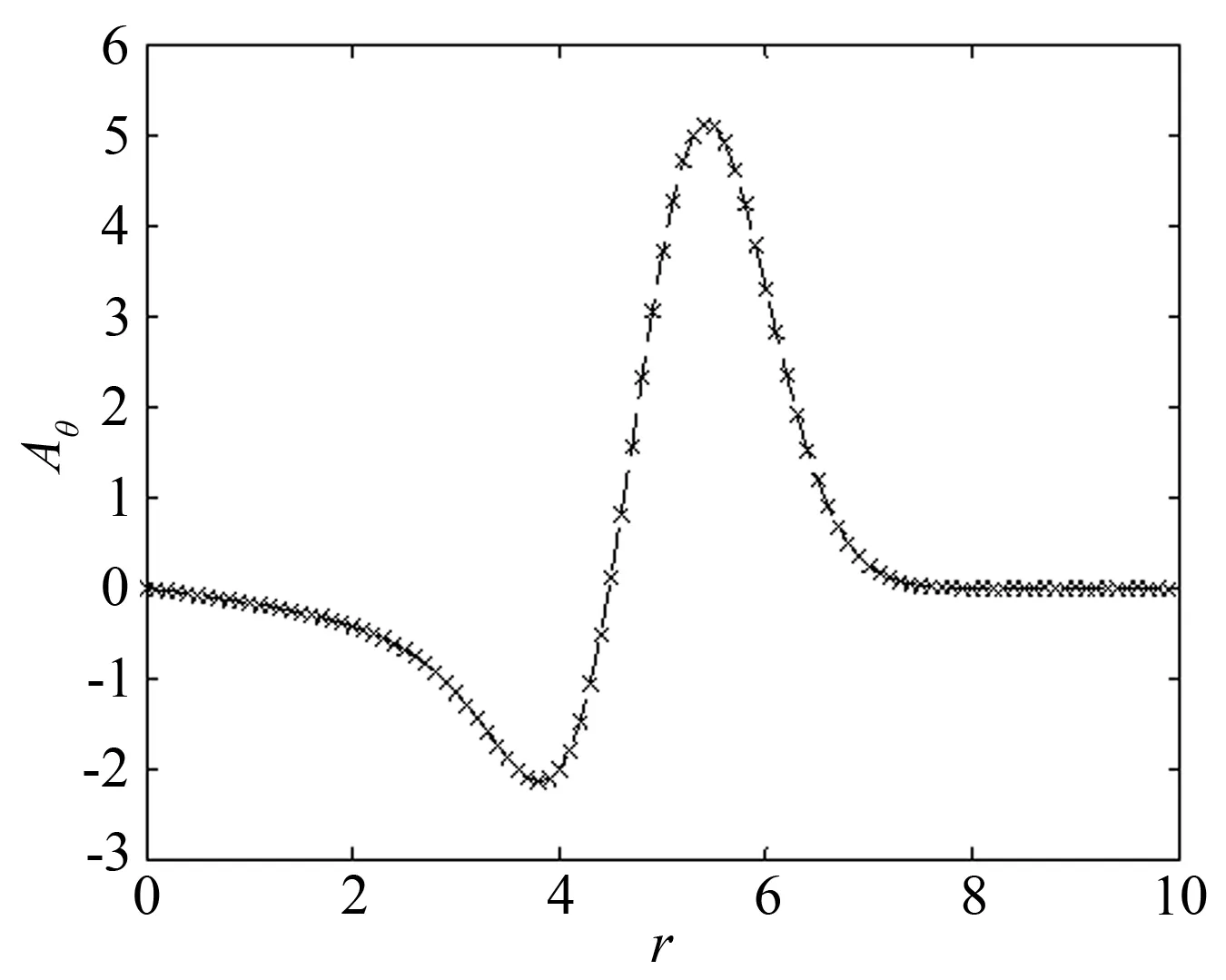
图3 假想的偏转角随半径变化示意图Fig.3 Artificial deflection angles

这里比较了直接积分法、迭代重建法、Abel逆变换和Radon逆变换对折射率分布重建的结果，如图4所示。其中Radon逆变换采用了MATLAB自带的算法，滤波函数为“Shepp-Logan”[13]。

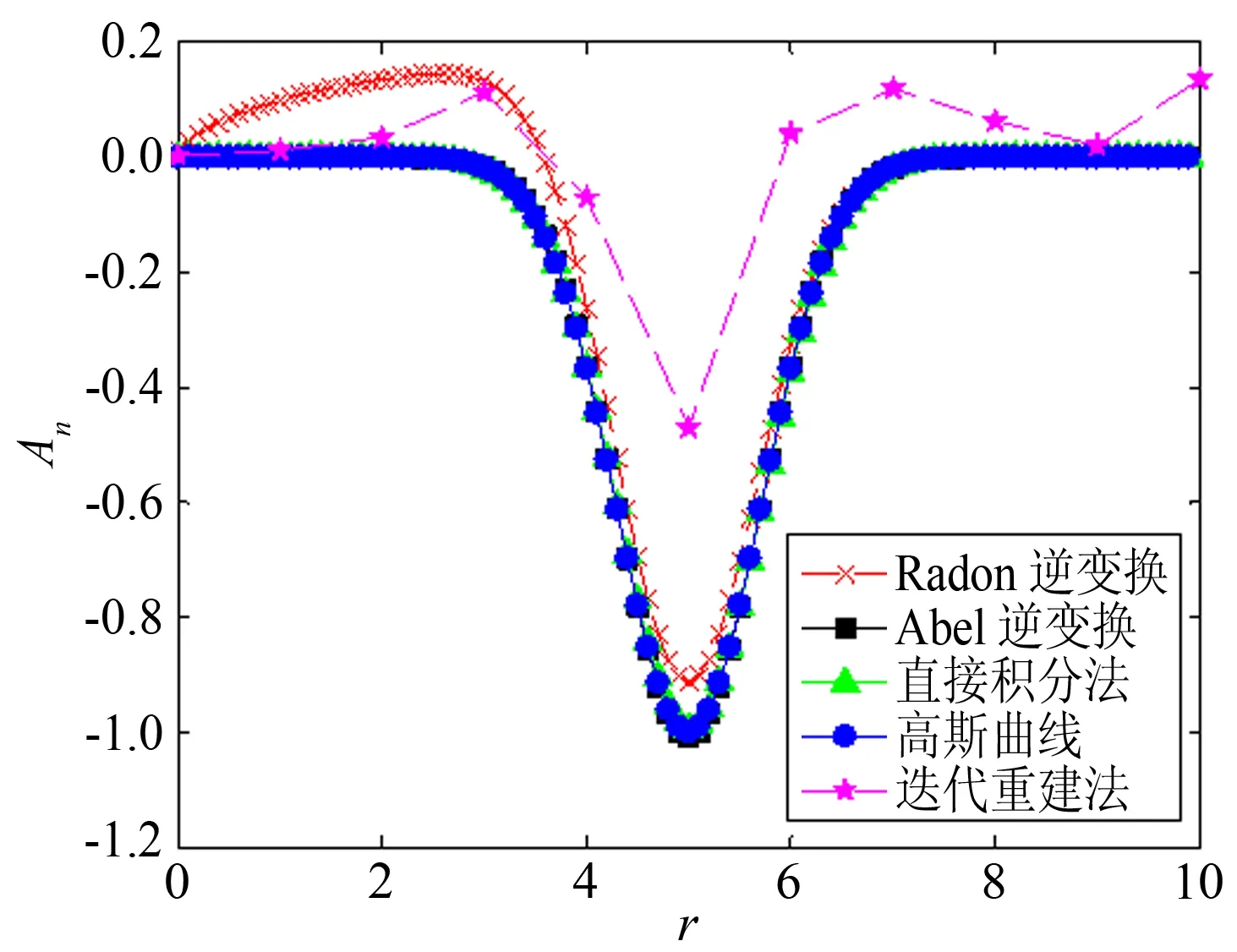
图4 算法比较Fig.4 Algorithm comparison

通过图4我们可以看到，直接积分法和Abel逆变换的结果基本和假想的高斯分布重叠，因此本文采用的是直接积分法。而Radon逆变换由于必须滤波，因此在接近半径为零时误差比较大。由于迭代法是直接积分法的离散近似，当数据点偏少时，误差较大。

2 实验设置

本文在“Z”型纹影基础上，采用标准光度法，通过一个垂直于管口的标定镜片来完成偏转角的定量测量。该透镜的焦距要足够的长，一方面是所标定的范围能够覆盖火焰偏转角；另一方面是满足：

(15)

式中:r是标定图像上像素在透镜上的对应半径,f是透镜的焦距，当焦距足够长时约等式成立[2]。这样，偏转角与图像灰度的定量关系就可以利用标定镜片来获得。标定的透镜半径为25.4mm，焦距10m(CVI Laser: PLCX-25.4-5151.0-C)。

图5 “Z”型纹影示意图Fig.5 Sketch of “Z” type schlieren system

在火焰点火前将镜片放置于火焰管口中轴线截面，也就是纹影系统的成像截面处，其x位置如图5所示，拍摄得到的标定纹影图片如图6(a)所示。然后，利用标定镜片得到的纹影图片建立图像灰度值和光线偏转角θ之间的关系。取图6(a)标定镜片纹影图像的中心线所在像素建立标定曲线如图6(b)所示，从而建立像素偏移值和灰度之间一一对应的关系。再通过(15)式，得到偏转角和灰度值之间的关系。

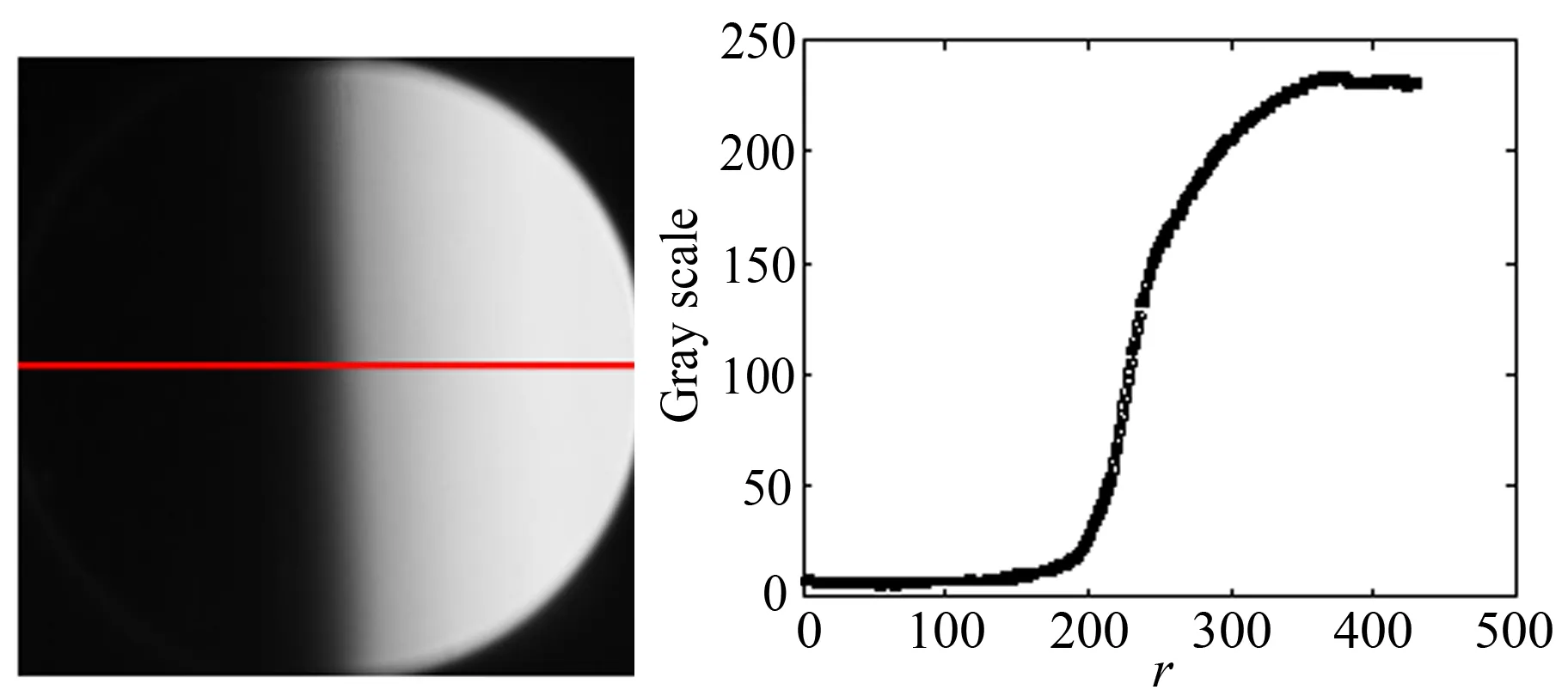
(a) 标定镜片的纹影图像 (b)标定曲线

图6 标定镜片的纹影图像及标定曲线

Fig.6 Schlieren image of calibration lens and calibration curve

火焰纹影图像的偏转角获得就是标定过程的逆向过程。将标定曲线建立的灰度值和偏转角关系，应用到火焰纹影图像的灰度值上，建立火焰纹影图像灰度值和其偏转角之间的对应关系。

在得到火焰偏转角之后，利用反演算法就能得到火焰折射率分布。再结合(4)式得到火焰温度。

实验中，光源采用的是LED灯。光线经过第一面抛物面反射镜形成平行光，平行光经过火焰后发生偏转，由于刀口的存在，偏向于y轴负方向(见图5)的光线被阻挡，最终在相机上呈现有明暗变化的纹影图像。

相机采用的是佳能EOS 550D。图像尺寸是2592pixel×1728pixel。拍摄标定镜片和火焰纹影图像时需要在相同的光照和相机设置下完成，确保所得到图像灰度值变化是由光线穿过不同物体所造成的。

火焰喷口是本生型，火焰为部分预混甲烷火焰，甲烷和空气的当量比为3。

3 实验结果

实验利用“Z”字形纹影系统，通过在同一条件下获取标定纹影图片和火焰纹影图像来完成。

图7(a)是火焰的纹影图像，所测温度位于管口上方h=12.96mm处，如图7(a)中红线所示。将图7(a)得到的火焰灰度曲线和由图6(b)得到的标定曲线对比，获得偏转角θ的值。图7(b)是热电偶测温示意图，热电偶在离管口同样的高度扫过一条直线。

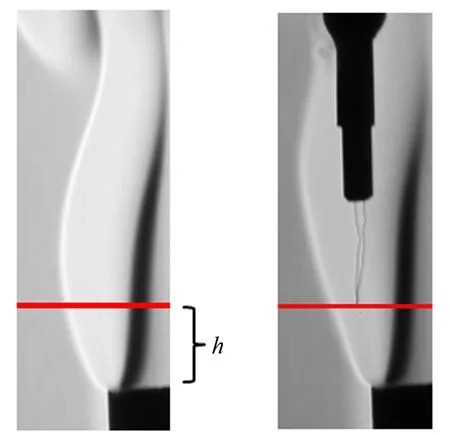
(a) 火焰纹影图像 (b) 细丝热电偶测量图像

图7 火焰纹影图像和细丝热电偶测量图像

Fig.7 Schlieren image of flame and the image of thermocouple measurement

实验中，采用直接积分法对图7(a)得到图像进行反演，得到离管口12.96mm处的火焰温度曲线。图8比较了纹影定量化所得到的温度曲线和细丝热电偶扫描得到的温度曲线。从图中可以看出火焰温度从预热区一直升高，在离管口轴线5mm附近发生化学反应，温度迅速上升，随着甲烷的燃烧耗尽，温度又急剧下降，在离管口轴线15mm附近基本恢复到环境温度。从图8可以看到，由纹影定量化得到温度曲线总体符合热电偶测温结果，在高温和接近管口轴线附近误差较大。这是由于高温时，气体组分变化剧烈，Gladstone-Dale常数为定值的假设会带来偏差[15]。

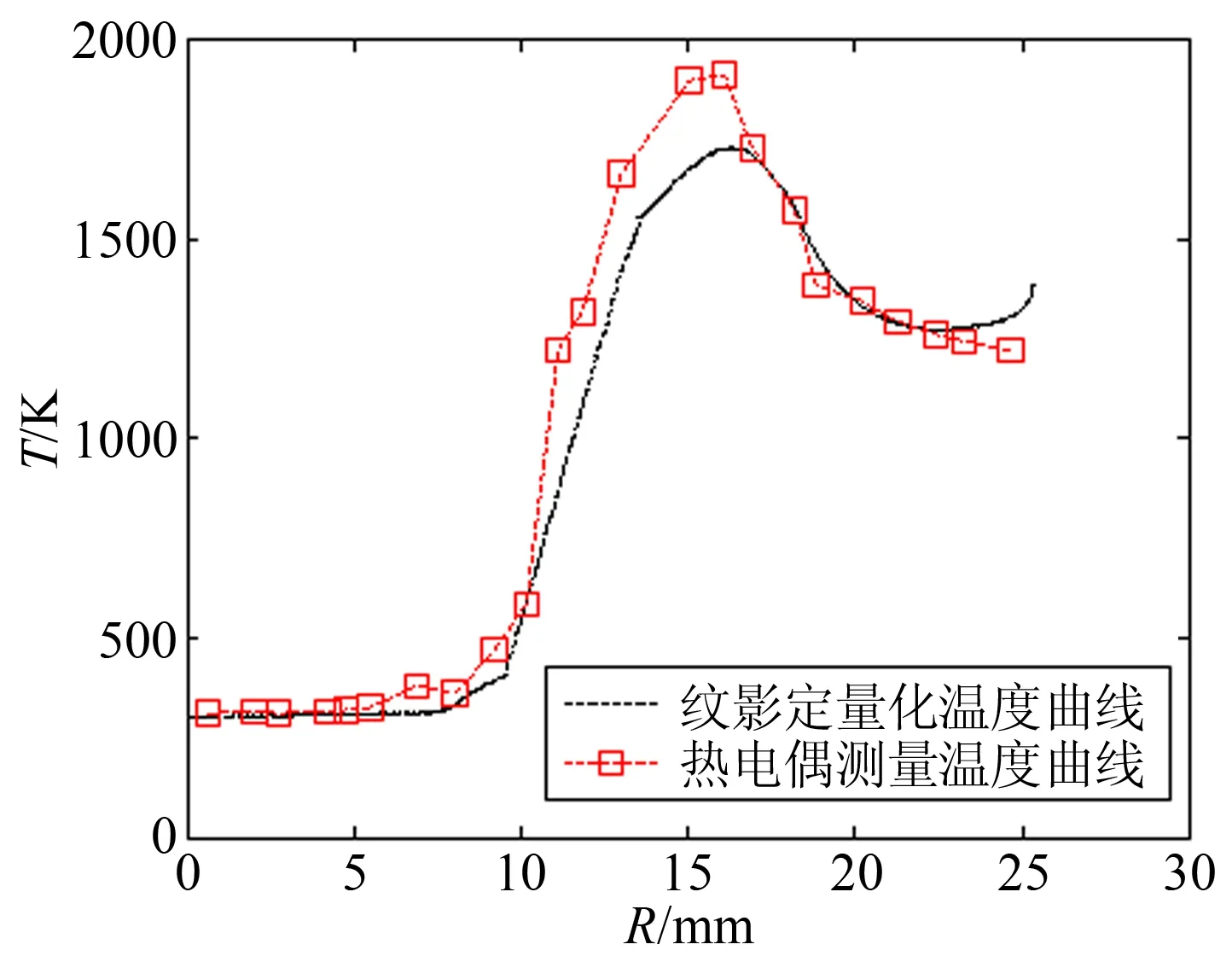
图8 纹影定量化和热电偶所测温度对比曲线

Fig.8 Temperature comparison of quantitative schlieren measurement and thermocouple measurement

4 结论

利用纹影的定量化得到了火焰的温度曲线。通过对比不同的反演算法发现，直接积分法和Abel逆变换的误差最小，原因主要为这2种方法都是直接对积分进行变换的。Radon逆变换常用于三维重建，在轴对称情况下，其滤波函数的选择会对原点附近的值产生影响。迭代重建法是对直接积分法的离散求解，其依赖于离散点的数量，数量越多误差越小，但同时过多的离散点会增加计算成本。由于用离散点代替了连续积分，迭代重建法因而可以回避积分所带来的奇点问题。

标准光度法利用一个标定镜片的纹影图像建立图像灰度值和光线偏转角之间的对应曲线。结果显示，采用标准光度法进行火焰纹影定量化得到的温度曲线总体符合由热电偶所测量的温度，证明了该方法对火焰温度测量的有效性。

更准确的纹影定量化依赖于对气体组分的测量，从而得到Gladstone-Dale常数的变化值。同样，尽量减少系统的光学误差，也能提高测量的准确性。

[1] Ajay K Agrawal, Nelson K. Butuk, Subramanyam R, et al. Three-dimensional rainbow schlieren tomography of a temperature field in gas flows[J]. Applied Optics, 1998, 37(3): 479-85.

[2] Michael J Hargather, Gary S Settles. A comparison of three quantitative schlieren techniques[J]. Optics and Lasers in Engineering, 2012, 50(1): 8-17.

[3] 叶继飞, 洪延姬. 轴对称流场的彩色纹影密度场定量测量[J].

红外与激光工程, 2013, 42(12): 3335-3338.

Ye Jifei, Hong Yanji. Quantitative measurement of density by color schlieren based on axial symmetry field[J]. Infrared and Laser Engineering, 2013, 42(12): 3335-3338.

[4] 周昊, 吕小亮, 李清毅, 等. 应用背景纹影技术的温度场测量[J]. 中国电机工程学报, 2011, 31(5): 63-67.

Zhou Hao, Lyu Xiaoliang, Li Qingyi, et al. Temperature measurement using the background oriented schlieren technique[J]. Proceedings of the CSEE, 2011, 31(5): 63-67.

[5] Pankaj S Kolhe, Ajay K Agrawal. A novel spectral analysis algorithm to obtain local scalar field statistics from line-of-sight measurements in turbulent flows[J]. Measurement Science and Technology, 2009, 20(11): 115402-115412.

[6] Schwarz A. Multi-tomographic flame analysis with a schlieren apparatus[J]. Measurement Science and Technology, 1996, 7(3): 406-413.

[7] Ishino Y, Horimoto K, Kato T, et al. 3D-CT measurement of premixed flames using a multi- directional quantitative schlieren optical system[J]. Procedia Engineering, 2013, 67: 303 - 316.

[8] Paul S Greenberg, Robert B Klimek, Donald R Buchele. Quantitative rainbow schlieren deflectometry[J]. Applied Optics, 1995, 34(19): 3810-25.

[9] Derek Dunn-Rankin, Felix Weinberg. Location of the schlieren image in premixed flames: axially symmetrical refractive index fields[J]. Combustion and Flame, 1998, 113(3): 303-311.

[10] Venkatakrishnan L, Meier G E A. Density measurements using the background oriented schlieren technique[J]. Experiments in Fluids, 2004, 37: 237-247.

[11] Pankaj S Kolhe, Ajay K Agrawal. Abel inversion of deflectometric data: comparison of accuracy and noise propagation of existing techniques[J]. Applied Optics, 2009, 48(20): 3894-3902.

[12] Deans S R. The transforms and applications handbook[M]. Boca Raton: CRC Press, 1996: 631-717.

[13] 邵华, 朱丹平, 吴毅雄. Abel逆变换的数值算法[J]. 上海交通大学学报, 2005, 39(8): 1375-1378.

Shao Hua, Zhu Danping, Wu Yixiong. Numerical methods of Abel inversion[J]. Journal of Shanghai Jiao Tong University, 2005, 39(8): 1375-1378.

[14] Shenoy A K, Agrawal A K, Gollahalli S R. Quantitative evaluation of flow computations by rainbow schlieren deflectometry[J]. AIAA Journal, 1998, 36(11): 1953-1960.

[15] Xiao Qin, Xu Dongxiao, Ishwar K Puri, et al. Aggarwal. Effect of varying composition on temperature reconstructions obtained from refractive index measurements in flame[J]. Combustion and Flame, 2002, 128(1-2): 121-132.

(编辑：李金勇)

Application of quantitative schlieren method in flame temperature measurement

Meng Sheng, Yang Zangjian, Wang Mingxiao, Shen Zhongliang, Deng Kai, Zhong Yingjie*

(Institute of Energy and Power Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

The frame temperature is measured using ‘Z’ type schlieren by standard photometric method. The relationship between the grayscale value of flame schlieren image and the deflection angle is established through a calibration lens. The refraction index is obtained by using axisymmetric assumption. Then by using the Gladstone-Dale relationship and the ideal gas law, the flame temperature is obtained. The comparison of involved inversion algorithms shows that, the direct integral method and the Abel inversion method can both achieve the least error, however, the Radon inversion strongly depends on the filter function and the algebraic reconstruction depends on the numbers of discrete points. The temperature reconstructed by the quantitative schlieren technique is compared to thermocouple measurements. The results prove the validation of this quantitative technique.

quantitative schlieren;temperature measurement;standard photometric method;abel inversion;radon inversion;algebraic reconstruction

1672-9897(2015)04-0065-05

10.11729/syltlx20140117

2014-10-11;

2015-01-07

浙江省科技厅基金资助项目(2014C31034)

MengS,YangZJ,WangMX,etal.Applicationofquantitativeschlierenmethodinflametemperaturemeasurement.JournalofExperimentsinFluidMechanics, 2015, 29(4): 65-69. 孟晟, 杨臧健, 王明晓, 等. 纹影定量化在火焰温度测量中的应用. 实验流体力学, 2015, 29(4): 65-69.

TB942