考虑批量订购的铁路客运动态定价研究

李煜

(西南交通大学交通运输与物流学院)

考虑批量订购的铁路客运动态定价研究

李煜

(西南交通大学交通运输与物流学院)

我国传统的铁路客运定价较少考虑旅客需求变化与运输能力的限制等条件，使用比较单一的价格制定机制，这种方式由于缺乏对市场需求反映，难以试下实现企业收益的稳步提升，同时也使得部分运输能力闲置。针对固定价格存在的缺陷，在考虑批量订购的基础上，针对分类的乘客需求建立了离散时间马尔科夫定价模型对高铁客运进行定价决策。应用最大凹向包络理论，对离散时间的多维马尔科夫模型进行了优化求解，并提出了市场需求变化时价格动态调整的策略，最后通过数值仿真验证了该模型的正确性。

收益管理;批量订购;铁路客运;最大凹向包络理论

1 基于马尔科夫决策的批量订购动态定价模型

1.1 问题描述与假设

(1)铁路公司销售一趟从A地直达B地的班列车票，在有限时间内完成销售，班列的座位容量有限。

(2)公司面临三种不同类型的顾客，第一类顾客为对价格非常不敏感，但对时间非常敏感，购票时选择购买高价票;第二顾客对价格非常敏感，对时间不敏感，倾向于购买低价票;第三类顾客对时间和价格均轻微敏感，选择购买中间价位车票。模型不考率低价顾客的升级购买行为。

(3)铁路公司针对不同车票进行定价，顾客到达后根据心理保留价格判断是否会购买车票。同一等级下顾客的心理保留价格独立同分布，且分布函数为已知的。

(4)顾客到达后以一定的概率进行批量购买，批量购买享受固定折扣，铁路公司设定最大购票数限制，限制倒卖车票行为。

(5)任何时间的订座需求是一个非负随机变量，并且不同时刻的需求相互独立。

(6)不考虑超售、退票和no－show(指:顾客购票后未成功乘车)

2.2 符号说明

建立模型需要如下的基本参数。

C为班列座位容量，即班列可装载的最大乘客数;t为决策阶段，0＜t＜T，t=0表示铁路公司开始销售车票，t=T表示销售的最后一期;i为顾客购买的座位等级，i=(1，2，…，I);pi为铁路公司针对第i个座位等级制定的价格。Λi=表示第i个座位等级的可行价格集，其中表示可行价格数目，不失一般性，假定:

(3)pi∈Λi=［1，2，3］，铁路公司针对第i个座位等级制定的价格从价格集Λi中选取。

N为预期全部类型车票产品的潜在顾客总数;βi为需求中i类顾客潜在需求的比例;为t时段需要i舱位票的潜在顾客需求到达率(到达率P=N/T，表示单位时间内到达的顾客)，且记表示没有顾客到达的概率;Vt(x)为在t时刻，各路段剩余座位容量为x的情况下，从开始销售到t时刻铁路公司能取得的最大期望收益;f(pi)为第i个座位等级顾客在面临车票价格为pi时购买概率分布函数，为对应的概率累积函数，记表示顾客购买的概率。记R(p)=P·(1－F(p))·p表示实际收益率。

P(y=j)表示顾客到达后购买j张车票的概率，记P(y=

Di(j)表示第i类顾客批量购买j张车票能享受的折扣。

1.2 模型

由假设知，铁路公司的售票期间内存在一个马尔科夫生灭过程。在该过程内，公司在离散时间下进行决策。将时间区间划分为足够多的决策阶段，使得在单位阶段内到最多到达一个潜在顾客。铁路公司通过定价影响消费者需求，在每个阶段，分别对不同类型的购票请求进行接受或拒绝，以实现销售期间内总收益最大。

为了便于分析和计算，设定足够大的离散时间阶段(T个阶段)，由此将时间区域［T，0］划分成单位长度为1的决策周期。假设在任意时刻t，公司面临剩余座位数量为K，则期望收益Vt(K)可以由前一阶段多个状态的收益转移而来。铁路售票公司面临的马尔科夫决策过程表示如图1所示。

图1 公司决策过程示意图

由图知，当决策期间内没有顾客到达时，Vt(K)由转移而来;当第i类顾客到达后，因车票售价超出其心理保留价格选择放弃购买的，由转移而来;当顾客到达后决定购买j张车票时，由转移而来。铁路公司选择接受或是拒绝购买的条件为(当且仅当)。

故T期间内，最大座位容量为C时，铁路公司能获得期望收益

式(1)的约束条件为:

(1)V0(x)=0，∀x∈［0，T］，这表明销售期开始前，不论剩余座位多少，期望总收益为零。

(2)Vt(0)=0，这表明，剩余座位为零的情况下，期望总收益为零。

定义一组包含所有产品的价格的数组为一个价格方案，那么记P*=arg max(VT(C))，P*∈Γ为最优价格方案，其中Γ为价格方案的全集。

1.3 求解简化过程——最大凹向包络理论

最大凹向包络定理:取任意k≥0，收益函数V(t，k)对任何预先确定的价格集合Γ，存在一组价格子集

Γ0∈Γ，Γ0={p1，p2，…，pnum}，满足:

(1)在价格Γ0下，R(λ)是的λ凹函数，单调递增;

(2)对任意价格Γ1，Γ0⊂Γ1⊆Γ，且Γ1≠Γ0，R(λ)不是λ的凹函数或者递增函数;

(3)如果pi∈/Γ0，任意时刻pi不能成为决定价值函数Vt(k)的最优价格。

2 算例求解和分析

本节通过数值仿真(利用Matlab2010b)展现模型的实际运用过程，分析市场供求关系、销售周期长短和最大运力对期望收益的影响。

基本参数如下:销售区间划分为T=1 000，车厢最大容量C为220，初始潜在顾客需求总数K为300，三二一等级顾客占总人数的比例βi=［0.4，0.5，0.1］

假设各ODF各座位等级允许的最大折扣Di=［0.8，0.9，0.95］

模型假设各ODF各等级顾客按照随机正态分布在销售区间内到达。且各产品需求分布概率函数应满足:1，则t时刻需求到达率，设fi(t)服从正太分布，且三类顾客的各自的到达概率密度服从图2(左)，从此可得到单位周期内的顾客到达率图2(右)。

图2 各类型顾客到达概率密度和到达率图

假定需求－价格反应函数f(x)服从指数函数，从而可以计算出顾客购买的概率为F(x)=φ·1/σ·e(－σ·p/u－1)，其中p代表产品价格，u为消费者心理保留价格的均值，σ为消费者价格弹性，φ为使得最低价格下购买概率为1的修正系数。

对每个产品，可选价格集为在最低价格和全价间均匀生成的num个价格的数组，本文仿真中num=10，由此计算出户Λ'=［pi·Di:(1－Di)pi/num:pi］，可选价格方案Γ的个数为10^3=1000组。本文使用最大凹向包络方法对价格方案集进行精简，精简后价格方案包含在数量为17的子集中，优化结果如图3所示。

图3 最大凹向包络优化结果示意图

将精简后的价格方案子集作为可选价格方案集进行迭代求解，搜索最优价格方案P*。

论文假设模型条件下，不同潜在需求总量下最优定价方案与最大期望收益见表1。

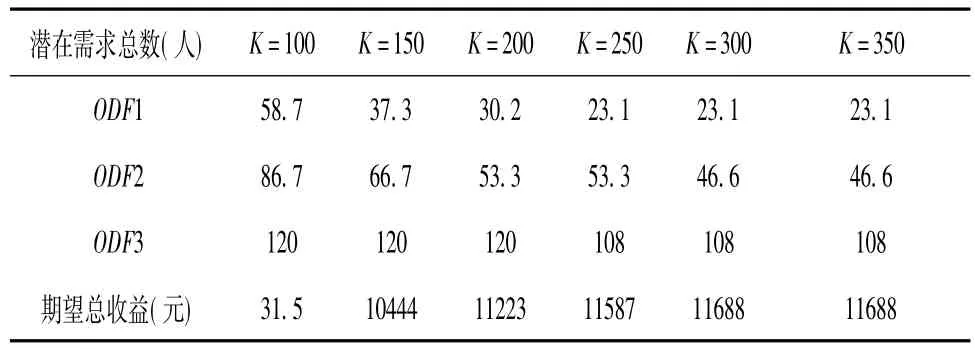
表1 不同潜在需求总量下最优定价方案与最大期望收益

由表1可知，当市场需求潜在总需求较小时，定价应采用低价策略以吸引顾客提升运载率，当市场需求上升，运能一定的情况下应提升定价，并可以优先提升价格敏感度较小的顾客人群的客票价格。

当K值不变(k=220)，网络运输下动态定价期望总收益和边际收益，随销售时长T和座位容量C变动情况如图4。

图4 总收益、边际收益随T、C值变化图

基于乘客分类的批量订购动态定价模型期望总收益特性如图5。

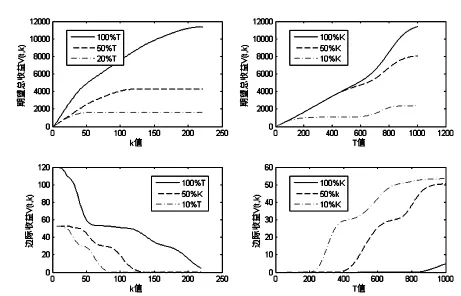
图5 总收益随、边际收益随T、C值变化剖面图

从图6可以看出，当T值不变，期望边际收益随C值的增加而减小;当C值不变，期望边际收益随T值的增加而增减。从原因上分析，这是由于当座位数一定，销售时长增加可以增大将座位销售给高价顾客的几率，从而使单张票的销售收益增加;而销售时常一定时，可供销售的座位越多，人们倾向于支付的购买价格就越低。

3 结论

本文建立考虑批量订购的马尔科夫动态定价模型，并通过算例实现论证了模型的正确定，这说明动态定价能有效提升企业收益，实现有限运输能力的利益最大化。本文将批量订购的因素引入到消费者购买行为中，从而避免了仅销售单张车票情况下潜在消费者流失的问题。本文暂未讨论消费者策略性购买行为，未来可进一步深入研究。

［1］ Gallego G，van Ryzin G.Optimal Dynamic Pricing of Inventories with Stochastic Demand over Finite Horizons［J］.Management Science.1994，40(8):999－1020.

［2］ Feng Y，Xiao B.Optimal policies of yield management with multiple predetermined prices［J］.Operations Research.2000，48 (2):332.

［3］ 罗利，萧柏春.航空客运平行航班动态定价模型［J］.中国管理科学.2012(03):104－111.

［4］ 李豪，熊中楷，屈卫东，等.基于乘客分类的航空客运座位控制和动态定价综合模型［J］.系统工程理论与实践.

［5］ 文曙东，张秀敏，王涛.运输网络最优价格组合研究［J］.武汉理工大学学报:交通科学与工程版，2005，29(1):133－136.

F532.5

C

1008－3383(2015)10－0164－02

2015－03－18