两种处理特大洪水参数公式的比较研究

杨立夫，贺 军

两种处理特大洪水参数公式的比较研究

杨立夫，贺 军

（河海大学水利水电学院，南京210098）

适线法是推求设计洪水的主要方法。文章对现有的含特大洪水情况下的统计参数公式和前人提出的由历史洪水资料和实测洪水资料推求频率曲线参数x，Cv的新公式进行对比讨论，论证在一定前提下现有公式较新公式的准确性，提出了改进意见。

统计参数；经验频率；历史洪水；适线法

1 概 述

在水利分析计算中，水文频率计算在防洪设计中有决定性的作用。推求设计洪水主要有两种方法：根据暴雨资料推求，根据流量资料推求。两种方法估计总体都受暴雨或流量资料观测年限影响，而如果能利用有效的特大值（历史洪水资料），会提高系列代表性［1］。

利用洪水或流量资料推求设计洪水时，主要采用适线法，而我国主要采用的频率曲线是P-Ⅲ型曲线，有论证表明，对于P-Ⅲ型曲线，若总体参数Cv0、Cs0愈大，采用极大似然法估计参数得到的在置信区间中的数据会存在更多无解样本，因此M-L法无法作为一个普通方法加以使用。实际应用中多采用矩法估计参数。使用适线法时，在将已有的洪水或流量资料进行大小排序计算经验频率后，要利用资料估计频率曲线的参数。笔者发现金光炎在文献中阐述现有的计算参数x、Cv的矩法公式存在一定误差，并提出改进的参数计算公式，但是笔者经实例论证发现在以最优适线结果为标准时，改进公式误差往往比矩法公式误差更大，并给出论证过程［2］。

2 现有的参数估计计算公式

对于有历史特大洪水和实测的洪水资料；xj为特大洪水，共a个（其中有1个为实测资料中的特大值）；xi为一般洪水，i＝l＋1，l＋2，…，n；N为实测洪水与历史大洪水一起构成的一个历史调查期为N年的样本。则整个样本统计参数x，Cv的无偏估计公式：

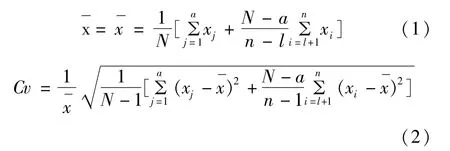
式中：xj为特大洪水，共a个，包括历史洪水和实测中的特大洪水（实测洪水中被调到为特大洪水的个数为l个，0＜l＜a），j＝1，2，……，a；xi为一般洪水，i＝l＋1，l＋2，…，n；N为实测洪水与历史大洪水一起构成的一个历史调查期为N年的样本。

再根据求得的参数，结合P-Ⅲ型频率曲线的离均系数值画出经验频率曲线，再目估调整曲线参数值，使上中部分的点与曲线尽量拟合。最后根据拟合最好的曲线计算设计洪水［3］。

3 前人提出的观点

由（1）式计算总体均值的无偏估计时，当N较大并且a较小时，均值的计算结果主要取决于实测系列的均值x（n），它在公式中所占权重很大。所以实测系列均值的代表性是十分重要的。

当l≠0（及有特大值从实测系列中抽出时），实测系列均值计算如下：

1）仅用余下的n-l项，即：

这样算得的值，可能偏小，因最大的l项不计在内。（现在普遍使用的矩法公式就是这样计算）

2）把l项仍留在实测系列内，均值计算结果为：

这个值可能偏大。

因此建议对l≠0时采用两种情况的平均值，及

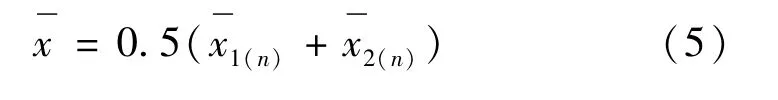
4 实例分析

4.1 数据来源

以金沙江屏山水文站1939—1978年40年的实测洪峰资料为例计算，吕振前在文献中给出利用钱-穆公式计算，并且根据频率曲线适线的结果，x0＝18100m3／s，适线曲线如图1所示。

4.2 假设情况

1）用现有公式计算得到x1（n）＝18 200 m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 300 m3／s，故这种情况下现有公式更准确。

2）假设数据还没有记录到1978年这么久，去掉1974—1978年的数据，重新组成历史调查期为115年的样本，假设x0＝18 100m3／s是一个理论总体平均值。

用现有公式计算得到x1（n）＝18500m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 600 m3／s，故这种情况下现有公式更准确。

图1 金沙江屏山站最大洪峰流量频率曲线

3）假设遗失一个历史洪水记录，去掉特大洪水值中1892年的数据，重新组成历史调查期为120年，特大洪水有 5个数据的样本，假设x0＝18 100 m3／s是一个理论总体平均值。

用现有公式计算得到x1（n）＝18 100 m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 200 m3／s，故这种情况下现有公式更准确。

4）去掉年代最久远1860年的数据，重新组成历史调查期为87年，特大洪水有5个数据，实测数据有40组的样本，假设x0＝18 100 m3／s是一个理论总体平均值［4］。

用现有公式计算得到x1（n）＝18 300 m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 400 m3／s，故这种情况下现有公式更准确。

5）去掉年代最久远1860年的数据，并且去掉1974—1978年的数据，重新组成历史调查期为82年，特大洪水有5个数据，实测数据有35组的样本，假设x0＝18 100 m3／s是一个理论总体平均值。

用现有公式计算得到x1（n）＝18 600 m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 600 m3／s，故这种情况下两种公式相差不大。

6）去掉年代最久远1860年和1892年的数据，重新组成历史调查期为74年，特大洪水有4个数据，实测数据有40组的样本，假设x0＝18 100 m3／s是一个理论总体平均值。

用现有公式计算得到x1（n）＝18 260 m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 300 m3／s，故这种情况下现有公式更准确。

7）去掉年代最久远1860年和1892年的数据，并且去掉1974-1978年的数据，重新组成历史调查期为69年，特大洪水有4个数据，实测数据有35组的样本，假设是一个理论总体平均值。

用现有公式计算得到x1（n）＝18 560 m3／s，而用新公式计算得到0.5（x1（n）＋x2（n））＝18 600 m3／s，故这种情况下现有公式更准确。

4.3 改进公式形式

原作者只给出实测资料部分公式的修正，没有给出样本整体估计参数的公式修正，现将修正后的公式列出如下：

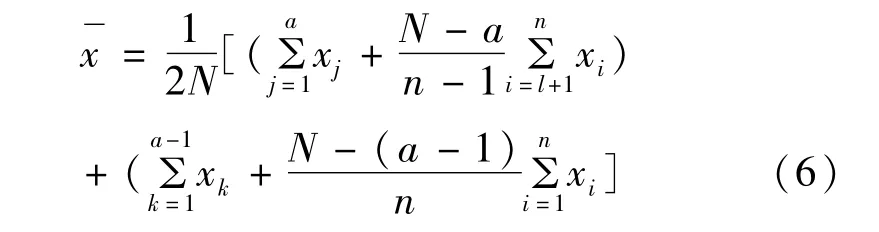
新公式中括号里的两部分与现有公式中括号里的部分都是根据线性比例放大得到的结果。而新公式猜想将实测数据中特大洪水放到实测数据而不在历史特大值中计算情况也计算一遍，再与原结果略偏小的公式加起来求平均值这样的结果会更加接近适线结果，但笔者尝试多种情况，发现新公式并没有预想中更精确［5］。

而吴燕，李松仕已提出了在不连续系列中参数Cv的修正公式，现列出如下：

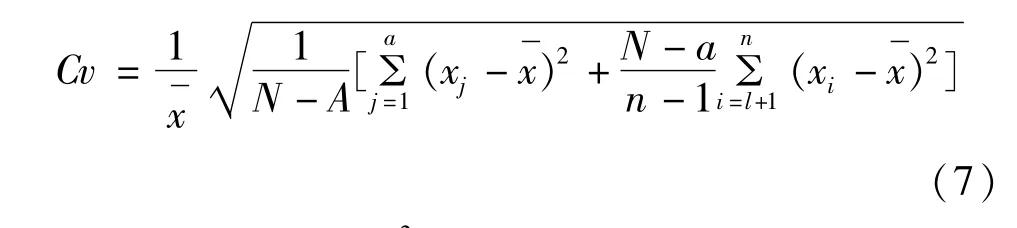
5 结 语

根据试算结果，在特大值的多少、实测数据的多少、总体样本的大小改变时都是现有矩法公式更加准确，所以推翻前人对改进公式x＝0.5（x1（n）＋x2（n））更加准确的猜测。在使用适线法估计洪水流量时还需要根据当地地理环境和计算者自身工作的经验对最后的曲线做一定的微调，各种方法都存在相对的误差，本文通过论证说明现有参数计算公式虽存在误差，但比起修正后的新公式，在实测洪水数据较多时较为精确，可减少试算调整曲线的工作量［6］。

［1］李刚，刘双林.关于有历史洪水参加的供水资料经验频率计算方法的讨论［J］.吉林水利，2003（02）：9-10.

［2］詹道江，徐向阳，陈元芳.工程水文学［M］.北京：中国水利水电出版社，2010：146-224.

［3］丛树铮，谭维炎等.水文频率计算中参数估计方法的统计试验研究［J］.水力学报，1980（03）：1-15.

［4］金光炎.频率分析中特大洪水处理的新思考［J］.水文，2006（03）：27-32.

［5］吕振前.关于洪水频率计算中的两个问题［J］.水文，1982（01）：20-23.

［6］吴燕，李松仕.不连序水文系列Cv计算公式的改进［J］.福州大学学报，1985（03）：151-156.

P333.6

A

1007-7596（2015）07-0033-02

2015-06-28

贺军（1969-），男，江苏宿迁人，讲师，博士研究生，从事水资源优化规划研究工作。