基于绝对矩块截断编码融合Clifford代数的图像压缩
2015-06-20齐兴斌李雪梅
赵 丽,齐兴斌,李雪梅,田 涛
(1.山西大学 计算机工程系,山西 太原 030013;2.北京航空航天大学 计算机学院,北京 100191;3.北京师范大学 教育信息技术协同创新中心,北京 100875)
基于绝对矩块截断编码融合Clifford代数的图像压缩
赵 丽1,2,齐兴斌1,李雪梅1,田 涛3
(1.山西大学 计算机工程系,山西 太原 030013;2.北京航空航天大学 计算机学院,北京 100191;3.北京师范大学 教育信息技术协同创新中心,北京 100875)
针对现有的图像压缩方法很难兼顾压缩效率和压缩后图像质量的问题,提出了一种基于绝对矩块截断编码和Clifford代数的融合方法。首先,将原始图像分为若干大小相等且互不重叠的局部小块;然后,利用绝对矩块截断编码保留每个子块的第一和第二矩;最后,利用Clifford代数将图像矩阵表示为最大完全平方和,并利用解码器重构图像。压缩实验结果表明,该方法的峰值信噪比可接近100 dB,结构相似度接近1,相比其他几种较新的方法,该方法取得了更好的压缩图像质量,并且降低了压缩耗时。
图像压缩;绝对矩块截断编码;Clifford代数;峰值信噪比;加权峰值信噪比
图像压缩技术通常利用较小位数表示图像,并且保证分解图像的视觉质量不产生明显下降。该技术大致可分为两类:有损压缩和无损压缩[1],无损压缩中重构图像与原始图像之间每个像素上都没有差异,有损压缩中重构图像包含相对于原始图像的退化[2]。无损压缩技术中压缩图像的质量好,但是压缩率低,有损压缩技术可提供较高压缩率,但图像质量较低[3]。因此,提出一种可靠的方法既能保证压缩率又能提高图像的质量显得至关重要。
针对图像压缩问题,学者们提出了许多方法,例如,文献[4]提出了基于相邻系数、父系数与子系数之间统计相依关系的小波系数合理树结构,获得了更高的图像压缩质量。针对目前JPEG2000中最优截断嵌入式块编码器硬件实现效率低且占用大量资源问题,文献[5]提出了一种适于CCD相机图像压缩的位面编码器,与传统方法相比,平均PSNR提高了0.91 dB。文献[6]提出了一种块截断编码(Block Trunca⁃tion Coding,BTC)压缩算法,可压缩单色图像数据,实现了2bit/pixel的低计算复杂度,通过执行每个非重叠像素块的矩保留量化,从而在降低存储空间的基础上保证图像质量。文献[7]提出了绝对矩块截断编码(Absolute Moment Block Trun⁃cation Coding,AMBTC),该算法保留了较高的均值,统计开销是每个块需要保持均值和标准差,以非重叠块的较低均值作为量化输出,更加有效地解决了图像质量问题,然而,压缩过程中的耗时问题仍然没有得到很好的解决。受文献[6-7]启发,为了进一步改善图像压缩后的图像质量与压缩率,本文提出一种基于AMBTC和Clifford代数压缩方法,实验结果表明,本文方法获得了比BTC和AMBTC更好的图像质量。
1 块截断编码
块截断编码是一种流行的压缩数字图像的有损矩保留量化方法,它保留每个块的第一和第二矩[8],算法步骤如下:
第一步,大小为M×N的原始图像划分成大小为m×m(令 m=4)的非重叠块(C),每个块分开处理。令f(xi),xi∈C为像素的原始强度。其中,C表示那个块中图像平面的像素坐标集,而且令m2=k。


式中:m1表示一阶矩,即

第三步,块矩阵(B)可由如下描述的那个块每个像素的C0和C1计算。

式中:th视作m1,可由式(3)定义。
第四步,必须发出每个块的块矩阵(B)、均值(xˉ)和σ,这里σ表示块的标准差。
第五步,为了重构图像,将值a给由0标记的像素,将值b给由1标记的像素,a和b满足

求解式(5)

对于每个块,m1,σ,k和k'已知,由此可计算值a和b。其中,k'是块矩阵中0的数目;k-k'是块矩阵中1的数目;0的数目k'由值a代替;1的数目k-k'由b代替。
2 本文方法提出
为了克服上述方法中的各种困难,本文提出利用Clifford代数融合AMBTC方法,Clifford代数[9]将一个正整数表示为正整数最大完全平方和,然后依次对整数的剩余部分重复同样的过程。
第一步,将像素大小为M×N的图像划分为若干大小为m×m的非重叠块子图像(正常为4×4像素),然后分开处理每个块。

说明假设值为:
{209,168,98,96,105,202,146,92,103,107,190,115,95,95,109}
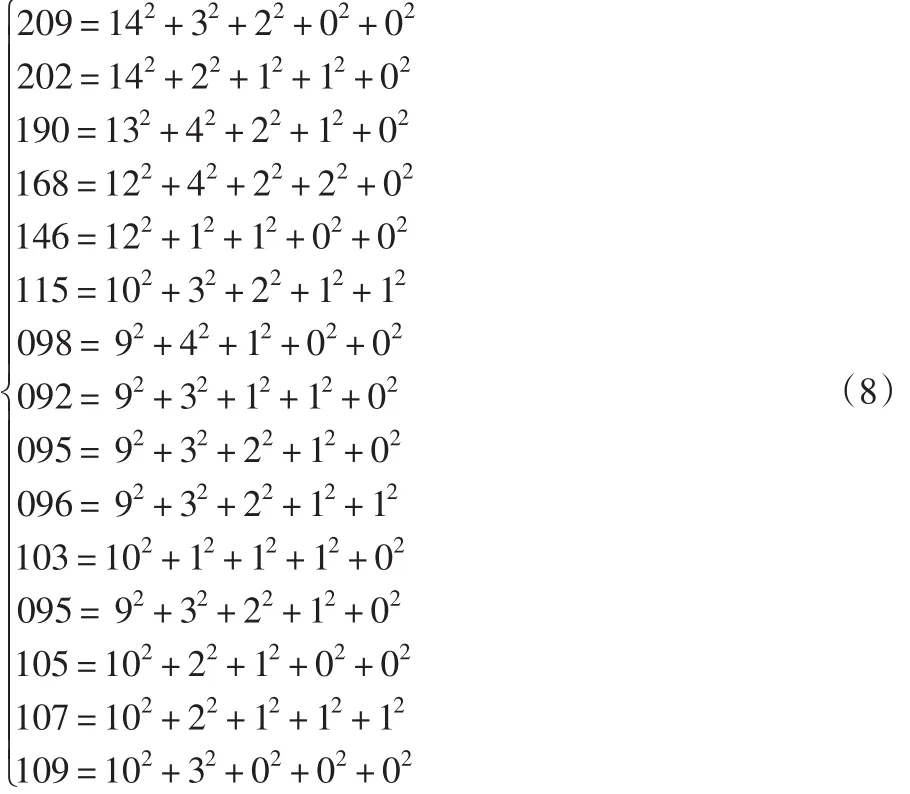
所以,第1列的期望值为102,第2列的期望值为32,第3列的期望值为12,第4列的期望值为12,第5列的期望值为02。
因此,最终向量元素的和vs=102+32+12+12+02=111,=120.625+0.267(120.625-111)=123.194 9。从各种实验结果巧妙选择α值使C-均值[11]与原始均值偏差较小,给出了更好的PSNR。
第三步,计算量化等级,并分类为两个范围,较高的C-均值为那些灰度等级大于或等于x~的集C0的C-均值,而剩余的C1用于产生较低C-均值。其中,C=C0⋃C1,C0⋂C1=∅。
较高C-均值由xH表示,较低C-均值由xL表示,计算如下
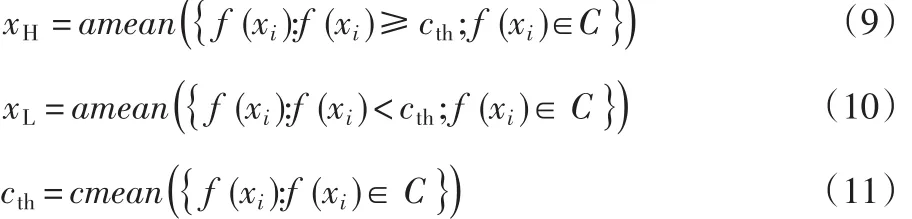
第四步,令cth为阈值,如果像素值 f(xi)小于量化阈值cth,则像素值量化为0;否则量化为1,二进制块称为B,用于表示每个像素的这些量化值。

第五步,块矩阵(B),必须给出每个像素的xH和xL。
第六步,解码器中,在位平面用xH代替1,用xL代替0来重构每个图像块。

本文方法需要16位编码位平面,这与BTC相同,但本文方法的编码器所需计算少于BTC,一个块所需的位总数为32,位速率为2 bit/pixel。
3 图像质量度量
本文方法的评价指标有峰值信噪比(PSNR)、加权峰值信噪比(Weighted Peak Signal To Noise Ratio,WPSNR)和结构相似度(Structural similarity,SSIM)。
3.1 峰值信噪比
PSNR[12]是信号的最大可能功率和原始图像与处理的图像之间逐点差之间的比率,定义为
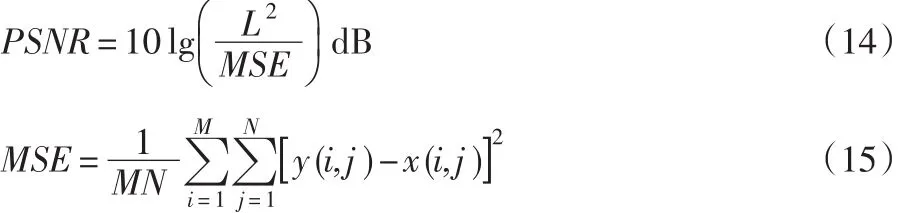
式中:L是像素值的动态范围;M和N是灰度图像的维度;x(i,j)和y(i,j)表示原始图像和处理的图像。如果参考图像和处理的图像彼此非常接近,则MSE将变小,PSNR将变大,否则PSNR值将变小,PSNR值范围可能从接近0到高达100 dB,如果参考图像和重构的图像彼此几乎相等,则PSNR将为100 dB,否则它将小于100 dB。
3.2 加权峰值信噪比
WPSNR[13]是一种不同于PSNR的量化指标,使用称作噪声可见函数(Noise Visibility Function,NVF),NVF的值范围从接近0到高达1,WPSNR定义为
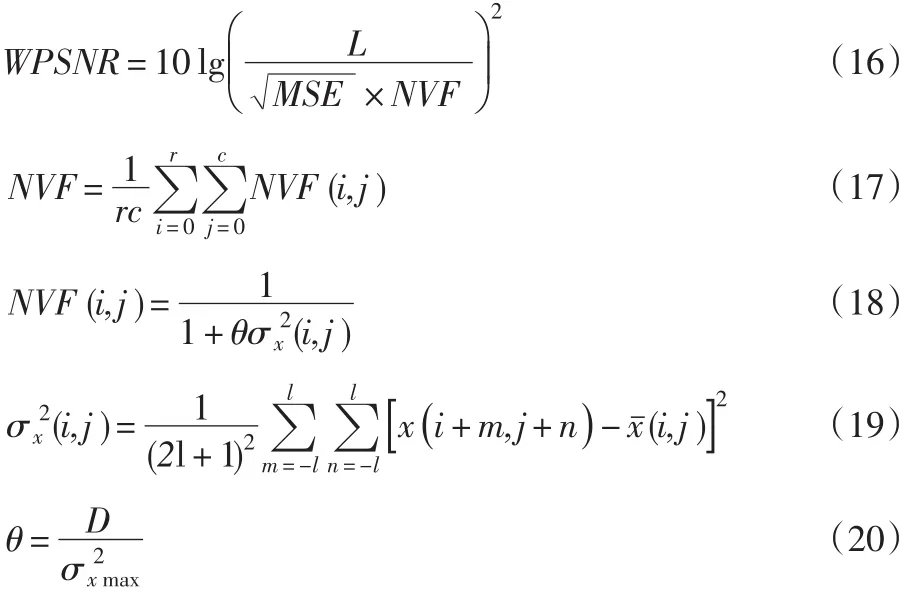
式中:σ2xmax是集中于像素坐标(i,j)的窗口中已知图像的最大局部方差;D∈[50,100]是决定参数,如果参考图像和重构的图像彼此相等,则WPSNR将为100 dB,否则它将小于100 dB。
3.3 结构相似度
SSIM[14]是另一种指标,用于确定参考图像和重构图像之间的相似度,SSIM指标测量图像质量,以初始未压缩图像作为参考,SSIM指标计算如下
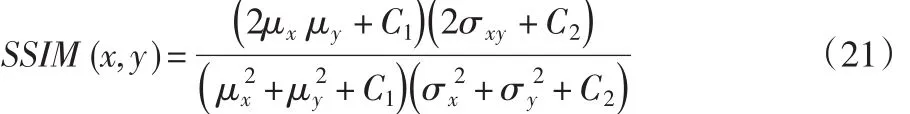
式中:

4 实验
实验使用6个大小为512×512的测试图像用于各种压缩技术的对比研究,分别为Lena,Peppers,Boat,Tank,Bridge和House。
4.1 参数分析
实验在Lena图像上分析了字块大小对本文方法压缩结果的影响,分别将图像分为4×4,4×5,5×5,5×6,6×6,计算其PSNR,WPSNR和SSIM,如图1所示,由于SSIM的值小于1,再而PSNR,WPSNR的值远大于SSIM,故图中给出的是放大100倍后的SSIM。

图1 子块大小对压缩结果的影响
从图1可以看出,随着字块大小的变化,3个指标先呈上升趋势,再呈下降趋势,总能在某处取得峰值,从图中可以看出,当字块大小在5×5时,可取得各个指标的最佳值,因此,后续实验均设置字块大为5×5。此外,可以看出,随着字块大小的变化,各个指标的变化并不是很明显,一定程度上体现了本文方法的稳定性。
4.2 实验结果
为了更好地评估本文方法,将其指标PSNR,WPSNR和SSIM与其他几种方法进行比较,每个子块大小设置为5×5,针对各个比较方法进行实验,实验结果如表1所示。
从表1可以看出,相比其他方法啊,本文方法在大部分情况下PSNR、WPSNR和SSIM值更大,PSNR值比AMBTC方法平均高出3 dB,WPSNR值比AMBTC方法平均高出4,SSIM值比AMBTC方法平均高出0.01,表明本文方法的压缩效果较好,从实验中观察到,本文方法压缩一张图像所用时间仅为0.032 1 s,而AMBTC和BTC方法的耗时均在0.2 s以上,表明Clifford代数将一个正整数表示为正整数最大完全平方和,有效地降低了压缩耗时。
图2~图7为原始图像和使用BTC、AMBTC、本文方法得到的压缩图像。
从图2~图7可以看出,相比原始图像,BTC方法压缩后的结果略显模糊,AMBTC方法压缩后的图像比原始图像稍暗,但整体效果较好,本文方法压缩后的图像与原始图像较为接近,取得了最好的压缩效果,再次验证了本文方法的优越性。
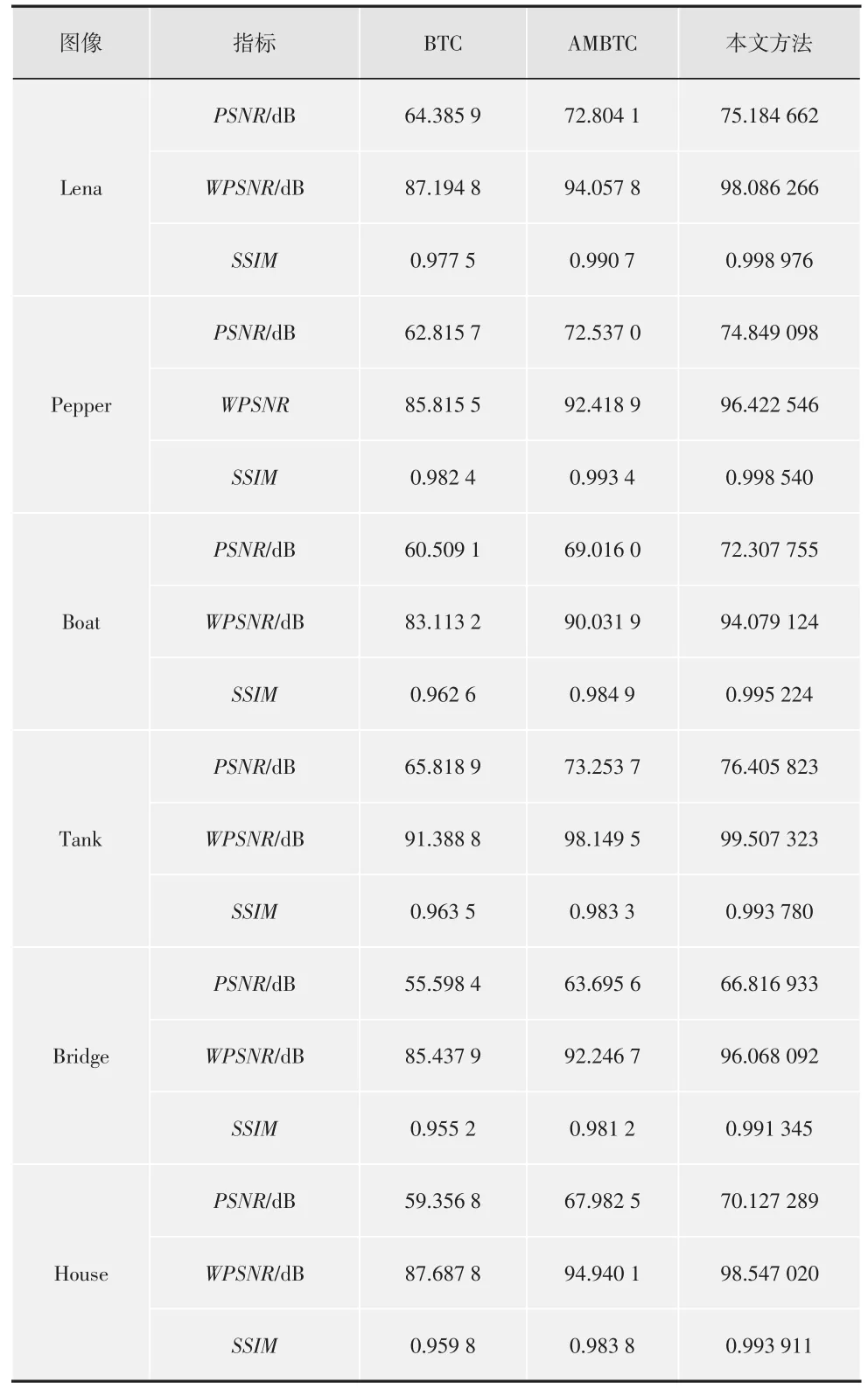
表1 各方法的PSNR,WPSNR和SSIM比较

图2 Lena上的压缩结果
5 结束语
本文提出了一种基于AMBTC和Clifford代数的图像压缩方法,将图像进行分块,并利用每个块的两个量化等级。实验数据库使用大小为512×512的灰度图像,参数度量用于比较和评估图像质量。实验结果表明,本文方法在PSNR和WPSNR方面改善了重构图像,通过灵活地选择α值,重构图像的PSNR明显优化,相比BTC和AMBTC两种方法,本文方法取得了更好的重构图像。
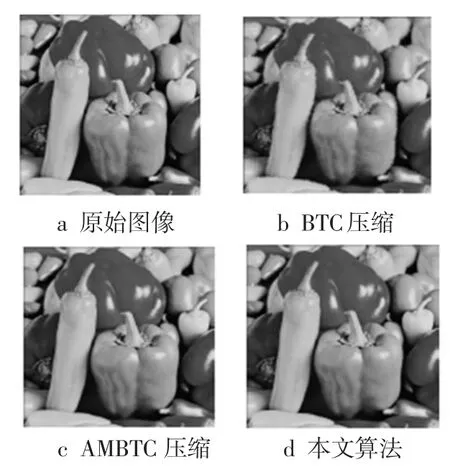
图3 Peppers上的压缩结果

图4 Boat上的压缩结果

图5 Tank上的压缩结果

图6 Bridge上的压缩结果

图7 House上的压缩结果
未来会将本文方法运用于其他图像的压缩,结合其他新颖技术,进行大量实验,在保证质量的同时,进一步提高压缩率。
[1] 李进,金龙旭,李国宁.离散小波变换域非负张量分解的高光谱遥感图像压缩[J].电子与信息学报,2013,35(2):489-493.
[2] ZHANG C,HE X.Image compression by learning to minimize the total error[J].IEEE Trans.Circuits and Systems for Video Technology,2013,23(4):565-576.
[3]李康顺,韦蕴珊,张文生.基于演化算法的卷曲DCT图像压缩[J].中国图象图形学报,2013,18(2):169-175.
[4] HOU X,YANG J,JIANG G,et al.Complex SAR image com⁃pression based on directional lifting wavelet transform with high clustering capability[J].IEEE Trans.Geoscience and Remote Sensing,2013,51(1):527-538.
[5]李进,金龙旭,韩双丽,等.适于CCD相机图像压缩的位平面编码器[J].电视技术,2013,37(2):135-142.
[6] CHEN W L,HU Y C,LIU K Y,et al.Variable-rate quadtree-segmented block truncation coding for color image com⁃pression[J].International Journal of Signal Processing,Image Pro⁃cessing&Pattern Recognition,2014,7(1):121-129.
[7]SUN W,LU Z M,WEN Y C,et al.High performance reversible data hiding for block truncation coding compressed images[J].Sig⁃nal,Image and Video Processing,2013,7(2):297-306.
[8]HU Y C,LO C C,CHEN W L,et al.Joint image coding and im⁃age authentication based on absolute moment block truncation coding[J].JournalofElectronic Imaging,2013,22(1):13012-13020.
[9]徐晨,刘辉,欧阳春娟,等.多光谱图像Clifford拟微分算子及应用[J].中国科学:信息科学,2012,41(12):1423-1435.
[10] SANDA A T,EZIN E C,GOUTON P,et al.Clifford algebra and gabor filter for color image texture characterization[C]//Proc.International Conference on Signal-Image Technology&Inter⁃net-Based Systems(SITIS),2013.[S.l.]:IEEE Press,2013:212-216.
[11]虞文俊,顾国华.一种基于模糊C均值聚类和边缘提取算法的红外偏振图像的模式识别方法[J].光子学报,2013,42(10):1244-1247.
[12]RUFAI A M,ANBARJAFARI G,DEMIREL H.Lossy medical image compression using Huffman coding and singular value de⁃composition[C]//Proc.Signal Processing and Communications Ap⁃plications Conference(SIU),2013.[S.l.]:IEEE Press,2013:1-4.
[13]PANGGABEAN M,RONNINGEN L A.Chroma interpolation us⁃ing windowed kriging for color-image compression-by-network with guaranteed delay[C]//Proc.International Conference on Digi⁃tal Signal Processing(DSP),2011.[S.l.]:IEEE Press,2011:1-6.
[14]桑庆兵,苏媛媛,李朝锋,等.基于梯度结构相似度的无参考模糊图像质量评价[J].光电子·激光,2013,24(3):573-577.
齐兴斌(1976—),硕士,讲师,主研图像处理、机器学习;
李雪梅(1962—),女,教授,主研图像处理、人工智能等;
田 涛(1980—),硕士,工程师,主研图像处理、机器学习等。
Research of Image Compression Based on Fusion of AMBTC and Clifford Algebra
ZHAO Li1,2,QI Xingbin1,LI Xuemei1,TIAN Tao3
(1.School of Computer,Shanxi University,Taiyuan 030013,China;2.School of Computing,Beijing University of Aeronautics and Astronautics,Beijing 100191,China;3.Collaborative&Innovation Center for Education Information Technology,Beijing Normal University,Beijing 100875,China)
For the issue that it is hard to juggle compression efficiency and the quality of compressed image when using traditional compressed methods,a fusion method based on absolute moment block truncation coding and Clifford algebra is proposed.Firstly,original images are divided into a number of non-overlapping local small pieces with equal size.Then,absolute moment block truncation coding is used to retain the first and second moment of each sub-block.Finally,Clifford algebra is used to represent image matrix to be the largest completely squares sum,and decoder is used to reconstruct image.Experimental results show that peak signal noise ratio and structural similarity of proposed method can achieve 100dB and 1 respectively,it has better compression quality of image and less time-consuming than several other advanced methods.
image compression;absolute moment block truncation coding;Clifford algebra;peak signal noise ratio;weighted peak signal to noise ratio
TP391 文献标志码:A DOI:10.16280/j.videoe.2015.06.004
【本文献信息】赵丽,齐兴斌,李雪梅,等.基于绝对矩块截断编码融合Clifford代数的图像压缩[J].电视技术,2015,39(6).
国家自然科学基金项目(61202163);山西省自然科学基金项目(2013011017-2)
赵 丽(1980—),女,硕士,讲师,主研图像处理、中文信息处理;
时 雯
2014-06-26
