巧解卫星变轨问题

朱志恒

卫星变轨问题是天体运动的综合问题，也是高考的常见题型之一。卫星变轨问题可分为突变与渐变两种情况。其中，卫星的突变问题知识点是学生比较难掌握的物理模型之一。这里讲一种高效解决卫星变轨问题的方法，将复杂的卫星变轨问题分解为几个简单的基本问题，并得出相应推论，在解题时只需把相关推论进行组合即可。

一、地球卫星在不同圆轨道上的相关推论

地球卫星做圆周运动的向心力由地球对它的万有引力提供。由基本方程易得：

定性分析可得：

推论1：做圆周运动的地球卫星，其向心加速度、线速度、角速度的大小均与轨道半径反相关，与卫星的质量无关；其周期与轨道半径正相关，与卫星质量无关。说明：该推论用于比较地球卫星沿不同圆轨道运行时相关运动学量大小。

二、地球卫星在椭圆轨道上的相关推论

由开普勒第二定律可知：

推论2：卫星沿椭圆轨道运行时，在远地点的速度最小，在近地点的速度最大。

由开普勒第三定律可得：

推论3：地球卫星的运行周期与其半长轴（半径）正相关。

说明：该推论用于比较沿椭圆运动的卫星与其它卫星的周期大小

三、地球卫星在不同轨道公共切点的相关推论

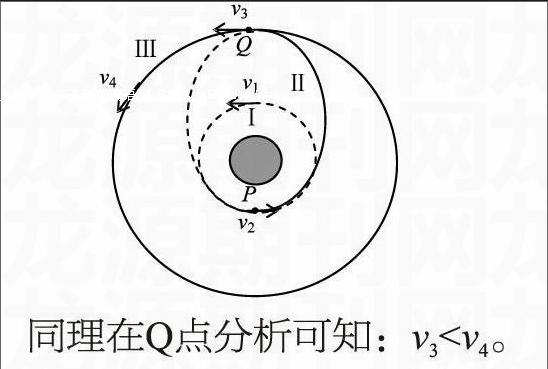
以一个椭圆轨道分别与两圆轨道相切为例。（如图）卫星在圆轨道Ⅰ上运行的线速度为v1，两圆轨道与椭圆轨道Ⅱ相切于椭圆轨道的近地点P、远地点Q，经P点时线速度为v2，经Q点时线速度为v3。在圆轨道Ⅲ上运行的线速度是v4。卫星沿轨道Ⅰ运行时，若要它经P点变到椭圆轨道Ⅱ，卫星应在P点做离心运动即万有引力小于卫星做圆周运动所需的向心力；注意到在同一点，卫星所受万有引力不变，可知卫星在该点所需的向心力要增大。再根据向心力公式易得卫星P点由轨道Ⅰ变到轨道Ⅱ时速度要增大，因此可知，v2>v1。

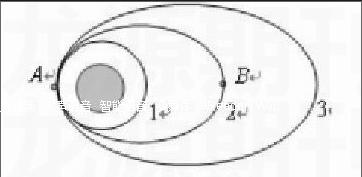
同理在Q点分析可知：v3

推论4：卫星沿不同轨道运动到公共切点处时，沿大轨道的速度较大。

说明：该推论用来比较不同轨道上的卫星经公共切点时的线速度大小

另外，由万有引力定律可知，同一卫星经同一点时合外力相同，则加速度相同；而两轨道相切于一点时，卫星的法向加速度恰等于其加速度，可知此时，二者的法向加速度（即向心加速度）也相同。综上可得：

推论5：卫星沿不同轨道运动至公共切点处时，加速度相同，向心加速度也相同。

典例分析：

例1：如上图（推论3中所用图）所示，卫星由圆轨道Ⅰ经椭圆轨道Ⅱ变轨至圆轨道Ⅲ，P、Q为椭圆轨道的近地点和远地点，v1、v4依次为圆轨道Ⅰ、圆轨道Ⅲ的线速度。v2、v3为卫星沿椭圆轨道Ⅱ经P、Q点时的线速度。则下列说法正确的是（ ）

A.卫星在椭圆轨道Ⅱ上经P点时的加速度比在圆轨道Ⅰ经P点时加速度大

B.卫星沿轨道Ⅱ经P点时的动能比沿圆轨道Ⅰ经P点时动能小

C.椭圆轨道Ⅱ的周期与圆轨道Ⅲ的周期相等

D.v1>v3

解析：由推论5知A错；由图可知椭圆轨道Ⅱ比圆轨道Ⅰ大，由推论4得卫星沿轨道Ⅱ经P点时的速度比沿圆轨道Ⅰ经P点时速度大，进而可知B错；椭圆轨道Ⅱ的半长轴小于轨道Ⅲ的半径，由推论3可知C错；由推论1知v1>v4，由推论4知v4>v3，联立得v1>v4>v3，D对。

例2：如图所示是“嫦娥一号”卫星绕地飞行的三条轨道，轨道1是近地圆形轨道，2和3是变轨后的椭圆轨道。A点是2轨道的近地点，B点是2轨道的远地点，卫星在轨道1的运行速率为7.7km/s，则说法正确的是：

A.卫星在2轨道经过A点时的速率一定大于7.7km/s

B.卫星在2轨道经过B点时的速率一定大于7.7km/s

C.卫星在3轨道所具有的机械能小于2轨道所具有的机械能

D.卫星在3轨道所具有的最大速率小于2轨道所具有的最大速率

解析：由于轨道1、2、3依次增大，由推论4得：卫星沿轨道1、2、3经过A点时线速度也依次增大，可知A正确；由推论4可知卫星在轨道2经B点的速度小于在轨道4的速度，因此卫星在轨道2经B点时的速度一定小于在轨道1的速度，故B错误；在A点，卫星的重力势能相等，而由推论4知卫星在轨道3经A点的速度大于在轨道2经A点的速度，可知C错误；由推论2知卫星沿椭圆轨道2、3运动时速度最大的位置都在近地点A，又由推论4知卫星沿轨道3到A点的速度大于卫星沿轨道2到A点的速度，可得D错误。

（作者单位：甘肃省张掖市第二中学）