页岩气藏三重介质模型压力动态分析及其应用

封钦亚，许艺博，张欣，刘静华，杜春雨，田玉明

（中国石油大学（北京）国家重点实验室，北京102249）

0 引言

国内外常规天然气的产量不断下降，开发的目标已经开始转向非常规资源，例如页岩储层中的页岩气。大多数页岩储层为天然裂缝储层，其蕴藏着20%以上的世界油气储量［1］，具有非常大的开发价值。常规储层一般由多孔并具有高渗透率的岩石组成，而页岩通常是一种具有极低渗透率的烃源岩，且页岩中产生的气体多为甲烷，一般困于微孔隙空间或者附着在页岩中的有机物质上，不易从中分离出来；所以，从页岩中开采气体是相当困难的［2-7］。为了估计页岩储层中的可采气体，就需要一个数学模型来描述气体在页岩中的流动过程。

在过去的几年里，双重介质模型已经广泛被用作解释气体在页岩基质和裂缝中的流动［5-7］。传统的双重介质模型假设所有的基质在整个流动系统中具有相同的性能，裂缝具有高的渗透率。双重介质首先是Barenblatt 等［8］1960年引入的，模型假定在基质和裂缝中流动为拟稳定流；后来，Warren 等［9］延伸了Barenblatt模型，通过瞬态试井分析，引入2 个无量纲参数（弹性储能比、窜流系数）来分别表示系统的储存油气能力、基质和裂缝系统中流体流动的难易程度；de Swaan［10］和Ozkan 等［11］分 别 于1976年、1987年 在 假 设 基 质 与裂缝间的流动为不稳定流动的基础上，提出了双重介质模型，但双重孔隙介质的缺陷在于忽略了基质中存在微孔隙、基质在整个系统中不是均质的。

页岩储层的天然气很大一部分来自于页岩基质。然而，页岩样品的渗透率太低，以至于在实验室内无法测量气体从页岩基质到裂缝的流动，因此，一些隐藏的流动通道不易被发现。为解释这种现象，近些年学者们提出来了一些假设。例如：Javadour 和Civan 等分别于2009年、2010年提出了分子扩散和Knudse 窜流作用［12-13］；F.P.Wang 等［14］2009年 提 出 了 在 页 岩 基 质 岩块中存在具有渗透性的白云岩石和天然的裂缝。

本文在F.P.Wang 等人假设的基础上，针对页岩气储层，提出了一个三重介质模型：考虑了页岩气吸附作用及一部分页岩基质具有渗透性；假设每个页岩基质是由具有纳米达西渗透率的微裂缝组成；气体在微裂缝中的流动机制主要是解吸；扩展了原有的瞬态和拟稳态双重介质页岩气模型。新的三重介质模型描述了页岩储层内部气体的流动行为。

1 页岩气吸附机理

页岩气与常规天然气藏的最主要区别是页岩气主要以吸附状态储存于页岩基质中。页岩气藏在孔隙中的解吸、吸附流动过程如图1所示。

图1 微孔内页岩气解吸、扩散、渗流分解过程示意

Langmuir 等温吸附曲线能描述在恒温条件下页岩气解吸与吸附的平衡关系，定量描述吸附气体的压力和被吸附量之间的关系。由于吸附是解吸的可逆过程，所以，等温吸附曲线可以表征页岩气的解吸特征。Langmuir 从动力学的观点出发，得出了单分子层吸附的吸附方程，即Langmuir 方程：

式中：VE为单位岩石体积的总吸附量，m3；VL为Langmuir体积，m3/t；pA为Langmuir 压力，MPa；pL为气藏压力，MPa。

2 数学模型的建立

三重介质模型的假设条件：

1）人工裂缝具有高渗透率和极小的孔隙度，是页岩气唯一流向井筒的介质。

2）页岩基质m 具有渗透性和孔隙性（带有微裂缝），并且向裂缝中提供气源。

3）页岩基质n 具有微小渗透性和孔隙性，并且既向裂缝又向页岩基质m 提供气源。

三重介质（裂缝、基质m、基质n）连续性方程分别为

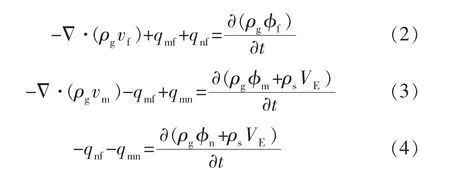
其中

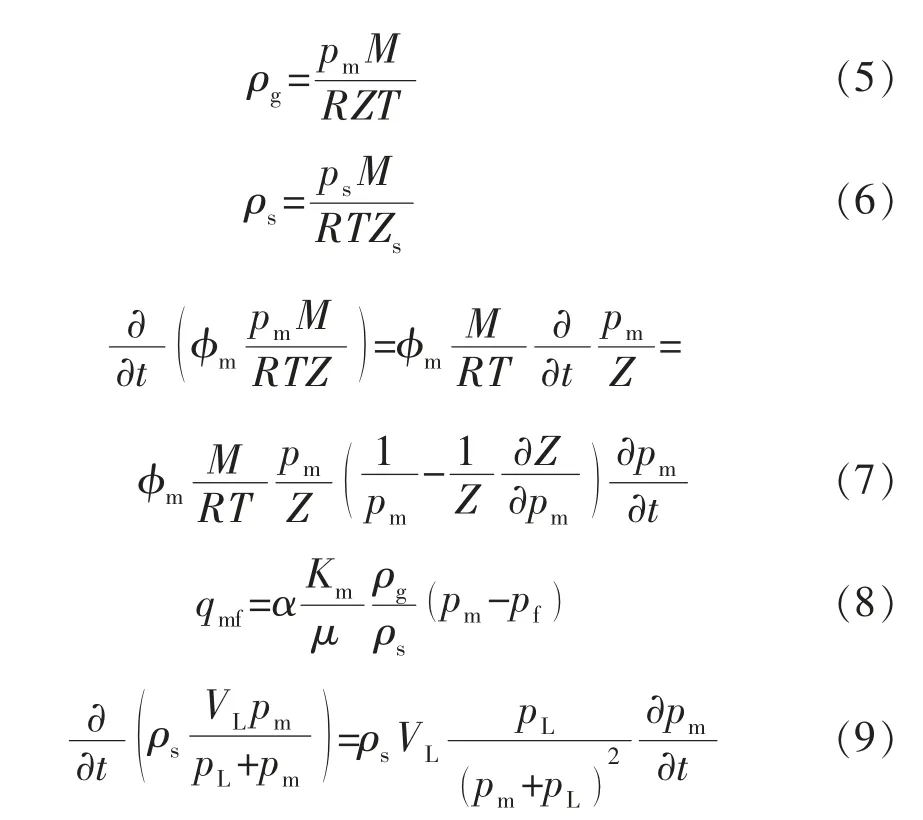
式中：ρg，ρs分别为气体和岩石密度，g/cm3；vf，vm分别为气体在裂缝中的流动速度和气体在基质中的流动速度，cm/s；t 为时间，d；qmf，qnf，qmn分别为基质m 系统与裂缝系统、基质n 系统与裂缝系统、基质m 系统与基质n 系统之间的窜流量，m3/d；φf，φm，φn分别为裂缝系统、 基质m 系统和基质n 系统的孔隙度；下标m，n，f分别代表基质m、基质n、裂缝。

将上述3 个连续性方程化简，并将引入连续性方程，则简化裂缝、基质m、基质n 的连续性方程分别为

其中

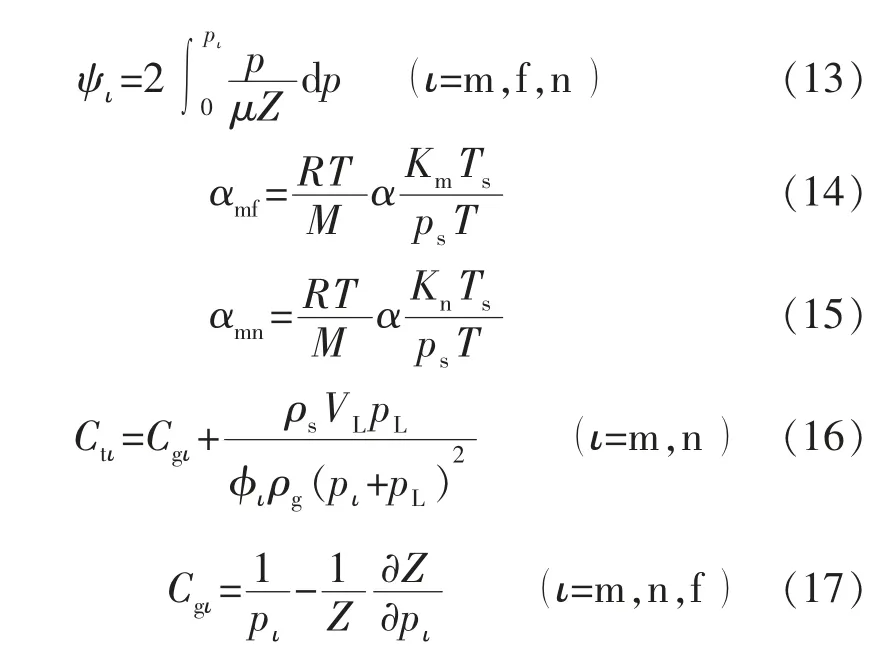
式中：K 为渗透率，μm2；ψ 为拟压力，MPa2/（mPa·s）；αfm，αfn，αmn分别为系统的形状因子（与基质m、基质n和裂缝的几何形状、裂缝的密集程度有关）；p 为压力，MPa；C，Cgι，Ct分别为压缩系数、系统原始压缩系数、综合压缩系数，MPa－1；μ 为气体黏度，mPa·s；ps为岩石颗粒压力，MPa；M 为气 体相对分子质量，g/mol；Z 为压缩因子；T 为气体温度，K；R 为通用气体常数，取值0.008 314 MPa·m3/（kmol·K）。

2 数学模型的解

以上建立的页岩气三重介质数学模型是一个复杂的非线性偏微分方程（组），无法用解析法直接求解，需将这类复杂的偏微分方程离散化后进行数值法求解［5-7］。

定义适当的初始条件和边界条件。初始条件：

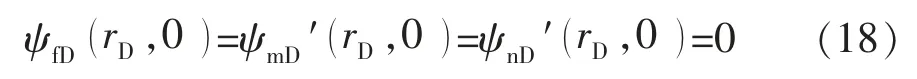
外边界条件：

内边界条件：

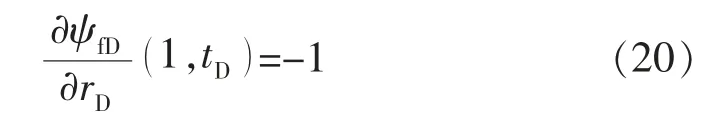
式中：ψfD为裂缝无因次拟压力；ψmD′，ψnD′分别为基质m、基质n 的无因次拟压力导数；rD为无因次距离；tD为无因次时间。

以基质m（考虑三维渗流）的连续性方程为例。

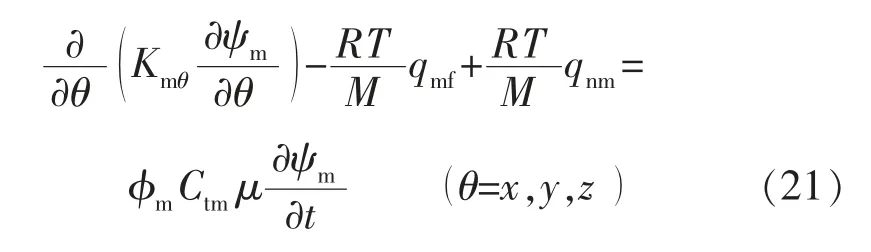
式中：x，y，z 为空间坐标。

1）对式（21）左边项进行差分。

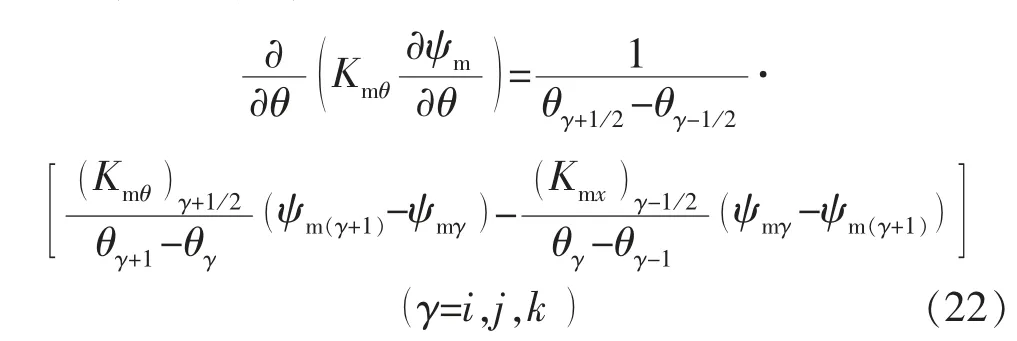
2）以x 方向为例。

令

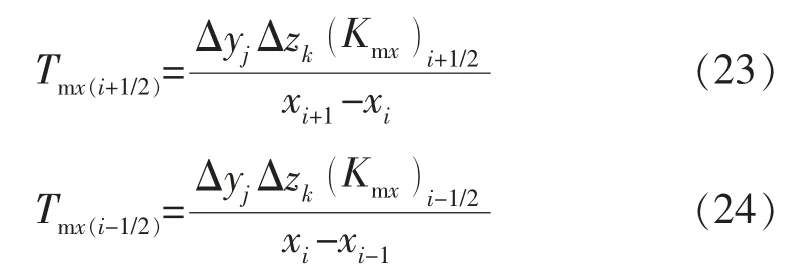
于是式（21）变成：

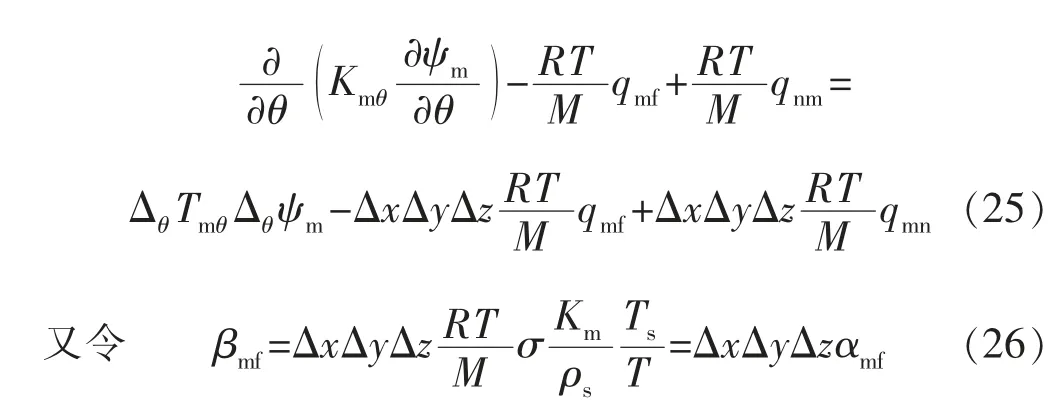
3）形状因子的简化。

αfn和αmn使用Warren 和Root 1963年［9-10］定义的：

式中：L 为基质岩块的特征长度，m；w 为裂缝面维数。

假设基质岩块呈正方体状时，岩块正方体单元的边长为αs，则w=3，L=αs，于是Ln分别为基质岩块和微基质岩块的长度，m）。对于αfm，使用Wu 等2007年［15］定义的：

式中：A12为单位体积岩石中裂缝和基质连接的面积，m2；L12为基质长度，m。

将基质块视为由微基质块包围的交叉网格块，并且裂缝厚度为l；因此，每个基质块都由长为Ln的微基质块组成，长为Lm［16-17］（见图2）。

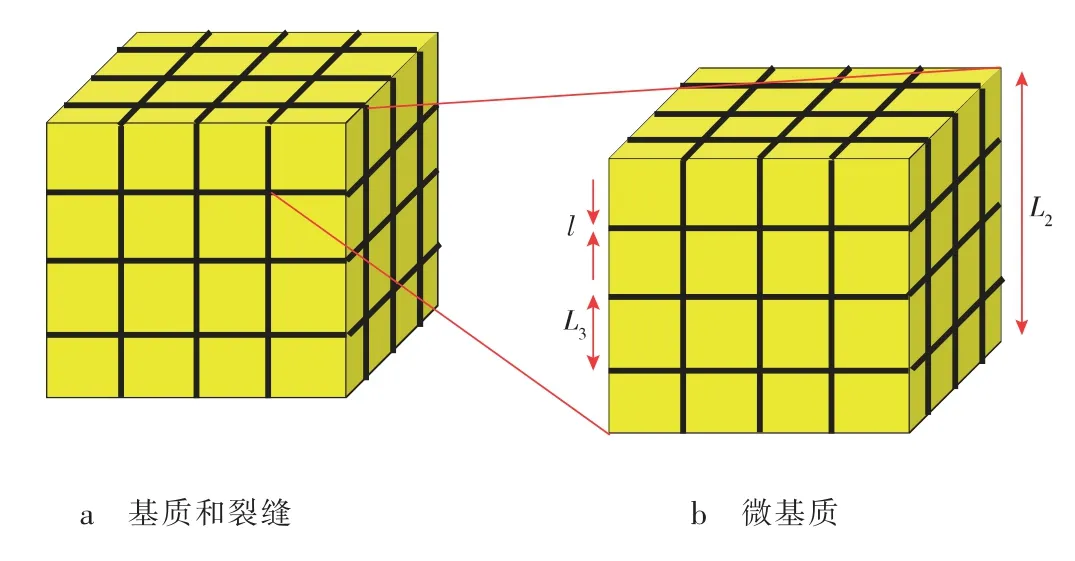
图2 基质理想化网格

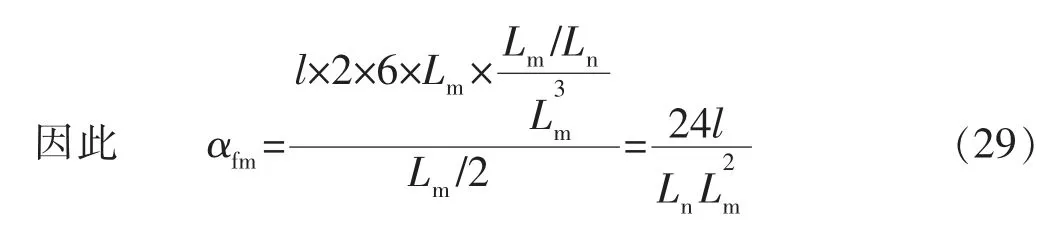
由式（21）的简化分别得到基质m、基质n 和裂缝的差分方程：

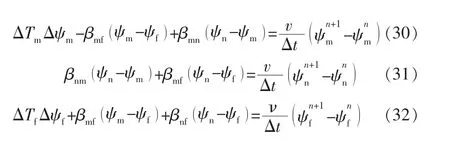
3 井底压力曲线分析

将式（30）、式（31）和式（32）进行Matlab 编程求解，对以下几种因素进行讨论。

3.1 窜流系数对井底压力变化的影响

图3a、图3b、图3c分别表示裂缝与基质m 间的窜流系数λfm、裂缝与基质n 间的窜流系数λfn、基质m和基质n 之间的窜流系数λmn对井底压力的影响，窜流系数的数值大小反映了原油在2 种介质间流动的难易程度。

图3 窜流系数对井底压力的影响

从图3中可以看出，窜流系数λ 越小，出现过渡段时期越晚，但整体形态不变。这说明：在三重介质模型中，当压力不断降低，发生基质m 向裂缝的窜流后，也将发生基质n 向裂缝的窜流；基质m 和基质n 系统只控制着气体的传播，它们之间的窜流系数几乎对井底压力没有影响。

3.2 储容比对井底压力变化的影响

图4a、图4b、图4c分别表示裂缝、基质m、基质n系统的弹性储容比（各系统储容系数与总储容系数之比）ωf，ωm和ωn对井底压力变化的影响。

图4 弹性储容比对井底压力的影响

从图4a可以看出：裂缝弹性储容比影响曲线的前半段，其值越小，其第1 个下凹越浅且越窄；ωf影响2条曲线间的关系，当ωf越小时，其第1 条曲线与第2条曲线的直线间距离就越小，这表明基岩与裂缝间的窜流时间就越长。从图4b、图4c可看出，基质m、基质n 系统的弹性储容比几乎对井底压力没有影响。

3.3 渗透率比值对井底压力变化的影响

图5表示的是裂缝渗透率与基质m 渗透率的比值K*对井底压力的影响。从图中可以看出，随着渗透率比值的增大，第1 条曲线和第2 条曲线之间的距离越来越大，同时第1 条曲线在图上变短且变高，表明基质与裂缝之间的窜流时间就越长。由于基质n 的渗透率特别小，所以可以忽略不计。

图5 渗透率比值对井底压力的影响

4 现场实际应用

以四川威远县龙马溪组的一口页岩气井为例。首先对这口井的储层特征、压裂参数、生产参数通过Eclipse 数值模拟软件进行历史拟合，之后采用本文所提出的页岩气三重介质模型进行模拟，最后与实际数据进行对比。基本参数如表1所示。

图6反映了考虑吸附解吸与不考虑吸附解吸对压裂页岩气井产能动态曲线的影响。页岩气藏考虑吸附解吸比不考虑吸附解吸产量递减更慢，且生产时间更长，产量更加稳定。

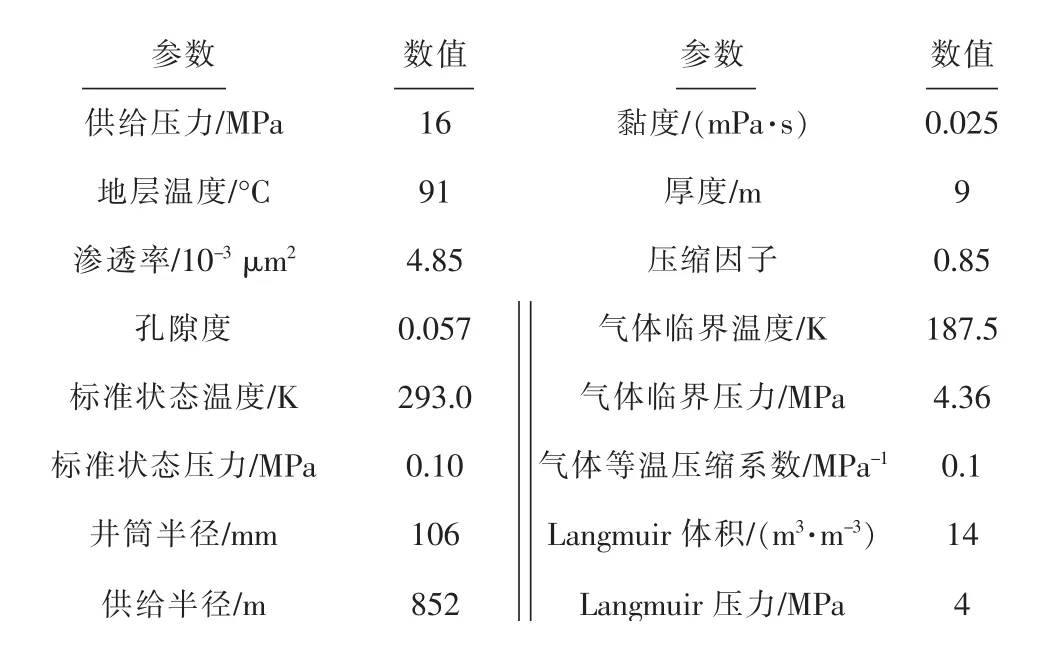
表1 储层参数

图6 吸附对产量的影响

通过现在页岩气实际数据和拟合数据进行分析（见图7），输入值和拟合值变化规律基本符合，相对误差在范围内，可以看出本文所建立的页岩气三重介质模型基本符合现场应用。

图7 页岩气实际数据和拟合数据分析

5 结论

1）页岩气藏比较复杂，且基质性能不同，本文所建立的三重介质模型考虑了页岩气吸附性能及微孔隙的存在，并通过离散差分及Matlab 程序进行求解。

2）分别分析了裂缝、基质、基质系统中的窜流系数、弹性储容比、裂缝与基质渗透率比值对井底压力特征曲线的影响：窜流系数决定出现过渡段时期的早晚，弹性储容比决定曲线下凹深度与宽度，渗透率比决定2条曲线之间的距离。这些结果可为以后页岩气藏开发提供试井模型和理论依据。

3）根据四川威远县龙马溪组页岩气井的现场数据，利用求得的模型进行计算。分析表明，实际数据与拟合数据基本规律一致。建立的模型得到有效验证。

［1］Sarma P，Aziz K.New transfer functions for simulation of naturally fractured reservoirs with dual-porosity models ［R］.SPE 90231，2004.

［2］Doddy Abdassah，Iraj Ershaghi.Triple-porosity systems for representing naturally fractured reservoirs［R］.SPE 13409，1986.

［3］Ali Al-Ghamdi，Chen Bo，Hamish Behmanesh，et al.An improved triple-porosity model for evaluation of naturally fractured reservoirs［R］.SPE 132879，2011.

［4］Escobar F H，Saavedra N F，Escorcia G D，et al.Pressure and pressure derivative analysis without type-curve matching for triple porosity reservoirs［R］.SPE 88556，2004.

［5］尹虎，袭问平，王新海.页岩气藏试井解释方法研究［D］.武汉：长江大学，2013.

［6］李登华，李建忠，王社教，等.页岩气藏形成条件分析［J］.天然气工业，2009，29（5）：22-26.

［7］陈更生，董大忠，王世谦，等.页岩气藏形成机理与富集规律初探［J］.天然气工业，2009，29（5）：17-21.

［8］Barenblatt G I，Zhelto I P，Kochina I N.Basic concepts of the theory of seepage of homogeneous liquids in fissured rocks［J］.Journal of Applied Mathematical Mechanics，1960，24（5）：852-864.

［9］Warren J E，Root P J.The behavior of naturally fractured reservoir［R］.SPE 426，1963.

［10］de Swaan O.Analytic solutions for determining naturally fractured reservoir properties by well testing［R］.SPE 5346，1976.

［11］Ozkan E，Ohaeri U，Raghavan R.Unsteady flow to a well produced at a constant pressure in fractured reservoir ［R］.SPE 19902，1987.

［12］Javadpour F.Nanopores and apparent permeability of gas flow in mudrocks（Shales and Siltstone）［J］.Journal of Canadian Petroleum Technology，2009，48（8）：16-21.

［13］Civan F，Rai C S，Sondergeld C H.Shale-gas permeability and dififfusivity inferred by improved formulation of relevant retention and transport mechanisms［J］.Transport in Porous Media，2010，86（3）：925-944.

［14］Wang F P，Reed R M，A.Pore network and fluid flow in gas shales［R］.SPE 124253，2009.

［15］Wu Y S，Ehlig E C，Qin G，et al.A triple-continuum pressuretransient model for a naturally fractured vuggy reservoir［R］.SPE 110044，2007.

［16］张利军，程时清，尹红军.双渗三重介质油藏试井分析［J］.特种油气藏，2008，5（15）：56-60.

［17］张冬丽，李江龙，吴玉树.缝洞型油藏三重介质数值试井模型影响［J］.西南石油大学学报：自然科学版，2010，6（32）：113-120.