基于Hasse图的概念格的一种渐减式构造算法

李海霞

（安徽新华学院公共课教学部,安徽合肥230088）

基于Hasse图的概念格的一种渐减式构造算法

李海霞

（安徽新华学院公共课教学部,安徽合肥230088）

提出了基于概念格Hasse图的一种对象渐减式构造算法,从Hasse图的最大节点开始,沿着仅包含该对象的路径,自顶向下完成概念格的构造,不需要遍历所有的节点,也不需要重新构造概念格.

概念格；Hasse图；节点；对象

自从德国的Wille教授1982年提出新式概念分析以来[1],作为其核心数据结构——概念格,已经在数据挖掘、知识发现、信息检索、软件工程、本体研究等很多领域得到广泛的应用[2-5].

在应用过程中,由于数据库中的数据是变化的、动态的,为了符合动态环境下概念格应用的需求,概念格维护的研究也是一个重要的方面.针对概念格的维护,已有的算法有：Godin提出了一种在新增对象的情况下,渐进式更新概念格的所有概念节点及其Hasse图[6]；李云、刘宗田等将原概念格节点按外延的势从小到大检查,通过不断增加属性完成概念格的更新[7]；曲立平等利用树结构组织节点,以此来减小更新节点及产生子格节点的搜索范围,提出基于属性的概念格的一种构造算法,减少了格的构造时间[8].

以上这些研究关注的是增加对象或者属性时的概念格的构造与维护,但随着概念格应用范围的不断扩展,需要研究在概念格中减少对象或属性时概念格的构造与维护,比如单位员工辞职、删除数据库中的一条记录等.近年,张磊等提出了自顶向下和自底向上两种基于概念格属性渐减的原理和算法,在原概念格的基础上直接更新概念格,比重新从形式背景构造概念格节省大量时间[9]；智慧来提出了对象渐减时概念格的维护算法[10],该算法中定义了唯一路径上的关键概念,但在对节点定位时需遍历所有的概念,这可能会影响算法的效率.

本文提出了基于概念格Hasse图的一种对象渐减式构造算法,从Hasse图的最大节点开始,沿着仅包含该对象的路径,自顶向下完成概念格的构造,不需要遍历所有的节点,也不需要重新构造概念格.

1 概念格的基本概念

研究需要用到文献[1]中的以下定义：

定义1一个形式背景K=（O,D,R）,其中O是对象集,D是属性集,xRy表示对象x具有属性y.

定义2设对象集A⊆O,属性集B⊆D,定义A'={m∈D|任意的g∈A,gRm},B'={g∈O|任意的m∈B, gRm}.若A、B满足A'=B,B'=A,则称二元组C=（A,B）为一个概念（或节点）,A称为概念C的外延（记为Ext（C））,B称为概念C的内涵（记为In（tC））.

定义3设C1=（A1,B1）和C2=（A2,B2）是两个概念,若A1⊇A2（等价于B1⊆B2）,称C1为C2的父概念（节点）,C2为C1的子概念（节点）,记为C1≥C2.形式背景K的所有概念按照这种偏序关系形成的格称为K的概念格,记为L（K）.若不存在节点C3,使C1≥C3≥C2,则称C1为C2的直接父概念（节点）, C2为C1的直接子概念（节点）,记为C1>C2.如形式背景1对应的概念格,如图1所示.

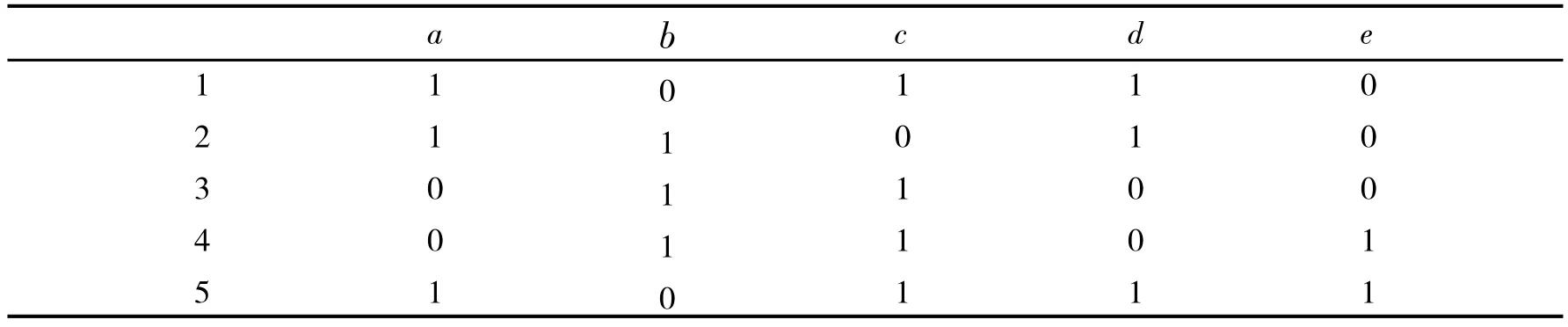
表1 形式背景1Tab.1 Formal context 1

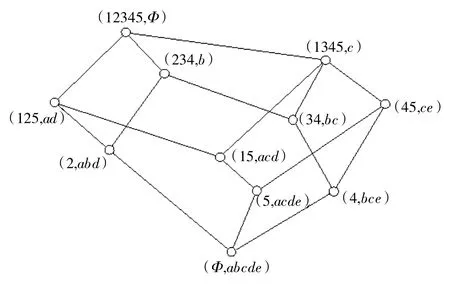
图1 形式背景1对应的Hasse图Fig.1 Hasse diagram of the formal context 1

2 基于Hasse图的概念格渐减式构造算法

2.1 相关定义及定理

为了研究减少对象a后概念格变化的规律,根据原概念格中每个节点C的外延和被消减对象a之间的关系,给出如下定义：

定义4如果a∈Ext（C）,则称C是不变节点.

定义5如果a∈Ext（C）,并且节点C的所有子节点的外延均不等于Ext（C）-a,则称C是更新节点.

定义6如果a∈Ext（C）,并且节点C的某一子节点的外延等于Ext（C）-a,则称C是删除节点.

设原概念格为L（K）,删除对象a后对应新概念格为L（K*）.

定理1若（A,B）为L（K）的不变节点,则（A,B）∈L（K*）.

证明：设（A,B）∈L（K）,且为不变节点,则a∈A,A'=B,B'=A.因为在原形式背景K和K*中,对应关系R不变,所以在新概念格L（K*）中仍有A'=B,B'=A,即（A,B）∈L（K*）.

定理2若（A,B）为L（K）的更新节点,则（A-{a},B）∈L（K*）.

证明：因为（A,B）∈L（K）,所以A'=B,即B为对象集A具有的所有共同属性；由更新节点的定义,a∈A,所以{a'}⊇B；外延减小,内涵增大,所以又有（A-{a}）'⊇B.

下证（A-{a}）'=B.若（A-{a}）'≠B,则（A-{a}）'∩（{a'}-B）≠椎,又因为a∈A,所以必有A'⊃B,与A'=B矛盾.即对象集A-{a}具有的所有属性为B,属性B对应的所有对象为A-{a},亦即（A-{a},B）∈L（K*）.

性质1若（A,B）为L（K）的删除节点,则其必有一个外延为A-{a}的直接子节点,且该直接子节点为不变节点.

证明：因为具有父子关系的两节点,外延至少相差一个元素,A-{a}仅比A少一个元素；由定义6,删除节点必然有一个子节点外延为A-{a},所以其必有一个外延为A-{a}的直接子节点.因为a∈A,由不变节点的定义,该节点为概念格的不变节点.

性质2设（A,B）为L（K）的删除节点,除了外延为A-{a}的直接子节点外,若还有其它直接子节点,则必为删除节点.

证明：记C=（A,B）,因为C若有其他直接子节点,外延不会为A-{a},即其他直接子节点不会为不变节点.设其他任一直接子节点为C1=（A1,B1）,若C1为更新节点（设在新格中对应的更新节点为C1*=（A1-{a},B1））,则a∈A1且C1的子节点中外延均不等于A1-{a}.因为C1

定理3设形式背景K*=K-{a},则概念格L（K）的不变节点和更新节点与新概念格L（K*）中的节点一一对应.

证明：设C1、C2∈L（K）,C1≠C2且为不变节点或更新节点,由定理2.1、2.2,显然在新格L（K*）中会对应不同C1*、C2*；

反设C*=（A*,B*）∈L（K*）,既不是原格L（K）中不变节点保留下来的,也不是更新节点更新过来的,而是原格L（K）中删除节点C=（A,B）对应过来的,则B*=B,A*=A-{a}.因为C为删除节点,由定义2.3和性质2.1,则a∈A,并且C有一个直接子节点C1=（A1,B1）,A1=A-{a}（该节点为不变节点,将保留到新格L（K*）中）.外延减小,节点内涵会增大,所以B⊂B1.对节点（A*,B*）、C1=（A1,B1）=（A1-{a},B1）∈L（K*）来说,二者外延相同,内涵不同,显然是错误的,所以假设不成立,即新格L（K*）中的节点必然是由原概念格中的不变节点保留下来的,或者是更新节点更新过来的.

由定理1、2、3,若删除对象a,对原概念格中不变节点保留,更新节点更新（外延减去a,内涵不变）,删除节点直接删除,就可以得到新格的所有节点,不需要重新构造概念格.

除了节点的变化,下面来确定节点之间边的变化.

定理4设C1、C2为概念格L（K）的不变节点或更新节点,并且二者在新概念格L（K*）中分别对应C1*和C2*.若C1

证明：设C1=（A1,B1）,C2=（A2,B2）,则C1*=（A1,B1）或（A1-{a},B1）,C2*=（A2,B2）或（A2-{a},B2）.因为在原格L（K）中不存在第三个节点C3=（A3,B3）,使B1B3B2,由定理2.3,新格L（K*）中节点是由原格L（K）中节点对应过来的,同样在C1*和C2*之间不会存在第三个节点C3*=（B3',B3）,使B1⊃B3⊃B2,所以C1*

由定理4,若直接父子节点均为不变节点或更新节点,则对应节点在新格中保持同样的直接父子关系,所以只要考虑删除节点的直接父节点和直接子节点有无直接父子关系.因为删除节点的直接子节点若为删除节点仍需删除,所以只要考虑该删除节点的直接子节点为不变节点（设为C1）的节点.在删除删除节点的各相应边时,若某一直接父节点到C1仍有其他路径连接,则不需要新增边；若无路径连接,则将该直接父节点到C1增加一条边.

2.2 基于Hasse图的概念格的对象渐减式构造算法

根据以上性质、定理,删除对象a时,从概念格的最大节点（该节点一定包含对象a）开始,对不包含对象a的直接子节点及其以下节点、边不做任何变化,对包含对象a的所有直接子节点,沿着概念格的Hasse图,自上向下,判断节点的类型,若为更新节点,外延减去a,内涵不变即为新格的节点,节点之间的边暂且不变.若为删除节点,删除该节点及各边；对该节点的直接子节点中的不变节点C1,若其某一直接父节点到C1仍有其他路径连接,则不需要新增边,若无路径连接,则将该直接父节点到C1增加一条边；对该节点的其他直接子节点因为也为删除节点,所以予以删除,边的处理同上.

算法步骤描述如下：

（1）从概念格的Hasse图取出最大节点,令A=A-{a}、B=B；

（2）取出节点（A,B）的一个不带标记“Y”的直接子节点,记为（A,B）；（标示“Y”表示该节点已经处理）

（4）若a∈A,并且节点（A,B）的所有子节点的外延均不等于A-{a}（,A,B）给以标示“Y”,令A=A-{a}, B=B,转向⑵；

（5）若a∈A,并且节点（A,B）的某一直接子节点的外延等于A-{a},节点（A,B）给以标示“Y”“S”,将外延为A-{a}的直接子节点标示为“Y”“B”,并判断该直接子节点与节点（A,B）的直接父节点有无路径连接,若有则不需要新增边,若无路径连接,则将该直接父节点到该直接子节点增加一条边,然后删除标示为“Y”“S”的节点；将其它直接子节点标记为“Y”“S”,均记为（A,B）,重复步骤⑸；

⑹若节点（A,B）的内涵B等于属性集D,将其和对应的直接父节点连边,结束.

这样就得到删除对象a后,新概念格的Hasse图,图中各节点即为新格的各个概念,不需要遍历所有的节点,不需要重新构造概念格,在原概念格Hasse图的基础上就得到新概念格的Hasse图,极大提高了概念格维护的效率.

3 举例

从形式背景1中删除对象{5},根据该算法,首先取出最大节点（12345,椎）,将其更新为（1234,椎）；沿着Hasse图向下,依次判断各个直接子节点：5∈{125}、5∈{1345}且节点（125,ad）、（1345,c）的各直接子节点外延均不等于A-{5},即二者为更新节点,分别更新为（12,ad）、（134,c）,均标示为“Y”；5∈{234},节点（234,b）为不变节点,标示为“Y”,其对应的Hasse图以下部分不作任何变化,也不再考虑；再取出带标示“Y”节点的各直接子节点：5∈{15}且其各子节点外延均不等于A-{5},即（15,acd）为更新节点,更新为（1, acd）标示为“Y”,5∈{34},（34,bc）为不变节点,标示为“Y”,其对应的Hasse图以下部分不作任何变化,也不再考虑；5∈{45},且有一直接子节点（4,bce）的外延等于A-{5}（为删除节点）,将节点（4,bce）标示为“Y”“B”,因为（4,bce）与该删除节点的直接父节点（1345,c）有路径连接,所以不增加边,然后直接将（45,ce）删除,最后将节点（45,ce）的其它直接子节点亦即（5,acde）标示“Y”“S”；取出（5,acde）所有直接子节点（只有一个（椎,abcde））5∈椎,即（椎,abcde）为不变节点,标示为“Y”“B”,将节点（1,acd）、（椎,abcde）之间连边,并删除（5,acde）又因为节点（椎,abcde）的内涵等于属性集{abcde},算法结束.

4 小结

本文提出了基于概念格Hasse图的一种对象渐减式构造算法,从Hasse图的最大节点开始,根据节点的类型,只需要沿着Hasse图的仅包含该对象的路径,自顶向下即可完成概念格的构造,不需要遍历所有的节点,极大提高了删除对象后概念格的构造效率.当然,实际工作中可能需要同时删除两个及以上的对象,这将是下一步的研究工作.

[1]Ganter B,Wille R.Formal concept analysis：mathematical foundation[M].New York：Springer-Verlag,1999.

[2]Li J Y,Mei C L,Lv Y J.Knowledge reduction in real decision formal contexts[J].Information Sciences,2012,189（15）：191-207.

[3]Mehdi K,Sergei O K,Amedeo N,et al.Mining gene expression data with pattern structure in formal concept analysis[J].Information Sciences,2011,181（10）：1989-2001.

[4]Qu K S,Zhai Y H,Liang J Y,et all.Study of decision implications based on formal concept analysis[J].Journal of General Systems, 2007,36（2）：147-156.

[5]Fethi F,Samir E,Ali J,et al.Formal context coverage based on isolated labels：An efficient solution for text feature extraction[J]. Information Sciences,2012,188（1）：198-214.

[6]Godin R,Missaoui R,Alaoui H.Incremental concept formation algorithms based on Galois（concept）lattices[J].Computational Intelligence,1995,11（2）：246-267.

[7]李云,刘宗田,陈崚,等.基于属性的概念格渐进式生成算法[J].小型微型计算机系统,2004,25（10）：1768-1771.

[8]曲立平,刘大昕,杨静,等.基于属性的概念格快速渐进式构造算法[J].计算机研究与发展,2007,44（S）：251-256.

[9]张磊,张宏莉,殷丽华,等.概念格的属性渐减原理与算法研究[J].计算机研究与发展,2013,50（2）：248-259.

[10]智慧来.概念格对象渐减维护与关联规则更新[J].计算机工程与用,2014,50（1）：21-23,35.

（责任编辑：卢奇）

A decreasing algorithm of concept lattice based on Hasse diagram

Li Haixia
（Department of Public Teaching,Anhui Xinhua University,Hefei 230088,China）

One decreasing algorithm of concept lattice was proposed,when one object was deleted.Based on the Hasse diagram,starting from the greatest node,along the path which only contains the object deleted,from top to down, the new concept lattice could be completed,without travelling all the nodes of the original concept lattice and reconstructing the new concept lattice from its corresponding formal context.At the same time,the new Hasse diagram can be obtained,too.

concept lattice；Hasse diagram；node；object

O153,TP301

A

1008-7516（2015）03-0057-04

10.3969/j.issn.1008-7516.2015.03.012

2015-04-07

安徽省自然科学项目（KJ2013B107）；安徽新华学院项目（2014zr011,2014zr014）

李海霞（1982―）,女,硕士,讲师.主要从事概念格尧智能信息处理研究.