棉织物透气性能的预测研究

徐瑶瑶，朱俐莎，杜 磊，邹奉元，b

(浙江理工大学,a.服装学院；b.浙江省服装工程技术研究中心，杭州 310018)

棉织物透气性能的预测研究

徐瑶瑶a，朱俐莎a，杜 磊a，邹奉元a，b

(浙江理工大学,a.服装学院；b.浙江省服装工程技术研究中心，杭州 310018)

采用两种计算孔径的方法，分别计算出织物孔径dp、dh。在特定纱线线密度下，研究织物孔径和织物透气率之间变化规律。其次改变纱线线密度，观察纱线线密度变化对织物透气率大小的影响。利用Origin软件拟合织物透气率与纱线线密度、织物经纬纱密度、孔径dp或孔径dh之间的函数关系。研究结果表明，当孔径分别采用dp、dh用作拟合参数时，所得函数计算的透气率与实测透气率的相关系数分别为0.9927、0.9952。由此可见，所建立的拟合函数可用于全棉织物的透气性预测。对于孔径计算方法的选择，采用dh时要比采用dp时，透气率的预测精度略高。

棉织物；拟合；透气性；相关性

织物透气性是指织物两侧存在压差时，空气从织物的孔隙透过的性能[1]。根据所需纺织品透气性需求，通过透气性预测，在投入生产之前便可准确进行织物的规格设定。因此织物的透气性预测对于纺织品的生产及使用具有指导意义。

目前，对于织物透气性预测主要有两类，一类是通过人工网络模型对所选取的影响因子进行拟合训练，利用神经网络能够对一类特定的织物较为准确地进行织物透气性预测。所采用的神经网络一般有BP神经网络[2]、RBF神经网络[3]、PPR神经网络[4]。3种模型中，PPR神经网络被认为拟合效果最佳。另一类是公式计算法，利用流体动力学原理、拟合得出预测公式，通过公式计算求得预测值。两类方法在特定训练样本下得到特定类型织物的透气性预测值都能达到一定的预测精度，但是公式计算法相对神经网络预测法有两大优点：一是相对更加泛化[5]，由于神经网络选取固定的影响因子作为输入层数据，输入层单元会自动计算权重，而不同的织物其透气性大小影响因子权重[6]会有所差异，公式计算法选用织物参数作为公式拟合依据，不受特定影响因子束缚，所以应用范围广；二是公式计算法相对简单方便，神经网络模型的建立相对复杂，专业性要求高。公式拟合许多数据处理软件均能直接应用，为非计算机专业学者进行相关研究提供诸多便利[4-6]。因此本文选取公式计算法，对棉织物透气性能进行预测研究。公式计算中的参数孔径有两种计算方法，对两种孔径计算方法通过拟合得出两种织物透气率预测公式，分析预测值和实测值之间的相关性，从而得到预测精度较高的一种织物透气率预测公式。

1 孔径计算方法

在公式计算法中通常采用的一个参数是孔径，孔径主要是为了表示织物纱线间孔隙的大小。研究思路不同对孔径的数学定义有所差异，而孔径的计算方法主要有以下两种。

1.1 孔径dp

Marie Havlova认为可以将织物经纬向交织所形成的孔隙理想化，假设每个孔隙为方形、大小相同且分布均匀,Dj、Dw(根/10cm)分别表示织物经向密度和织物纬向密度，dj、dw(mm)分别表示织物经向纱线直径和纬向纱线直径，定义dp为织物纱线间孔隙半径。可得孔径dp计算公式[7]：

(1)

1.2 孔径dh

织物其实是一种典型的多孔介质材料，空气透过织物的过程与流体流过多孔介质的过程相似,因此织物的多孔隙结构可以视为平行毛细管束集聚体模型[5,8]。通过流体力学原理，模拟织物间孔隙通道为圆形通道，可得圆形通道孔径dh计算公式[9]：

(2)

式(2)中：A为织物孔隙截面面积；p为织物孔隙截面周长。

计算织物孔隙截面面积及截面周长，可得孔径dh计算公式为式(3)：

(3)

2 实 验

2.1 试样

排除织物材质、组织结构对织物透气性的影响，选用全棉平纹织物共29块作为试样。其中21块为拟合样，8块为验证样。采用样本均由绍兴县纺业良纺织有限公司提供。具体织物规格详见表1。

2.2 测试数据及孔径计算结果

2.2.1 织物纱线直径测定

为了更好地表征织物纱线直径，采用江南永新MV2100金相显微镜获取经纬向纱线图片、利用Scope image9.0中的测量工具对同一纱线取10个有效点进行直径测量，取平均值，获取织物经纬向纱线表观直径[10]。如图1所示，测试结果见表2。

表1 样本织物结构参数

注：1～21为拟合样，22～29为验证样。

图1 纱线直径测试示意

2.2.2 织物厚度测定

利用YG(B)141D数字式织物厚度仪测量织物厚度L(mm)，样品在测试前放置于恒温恒湿室预调湿24h。测试过程选取10组有效点数据，取平均值。

2.2.3 织物透气率测定

使用YG461型织物透气仪进行织物透气率测试。测试条件：织物两侧压差设为100Pa，圆形测试试样的直径为20mm。

2.2.4 孔径dp、dh的计算

通过所给的公式(1)、公式(3)，将相关数据代入公式，计算得出每块样本的孔径dp、dh。其中织物纱线线密度T(tex)、织物经纬向密度由样本制造商提供，经纬向纱线表观直径由实验测量所得。

织物经纬向纱线表观直径、织物厚度、透气率及织物孔隙直径计算结果见表2。

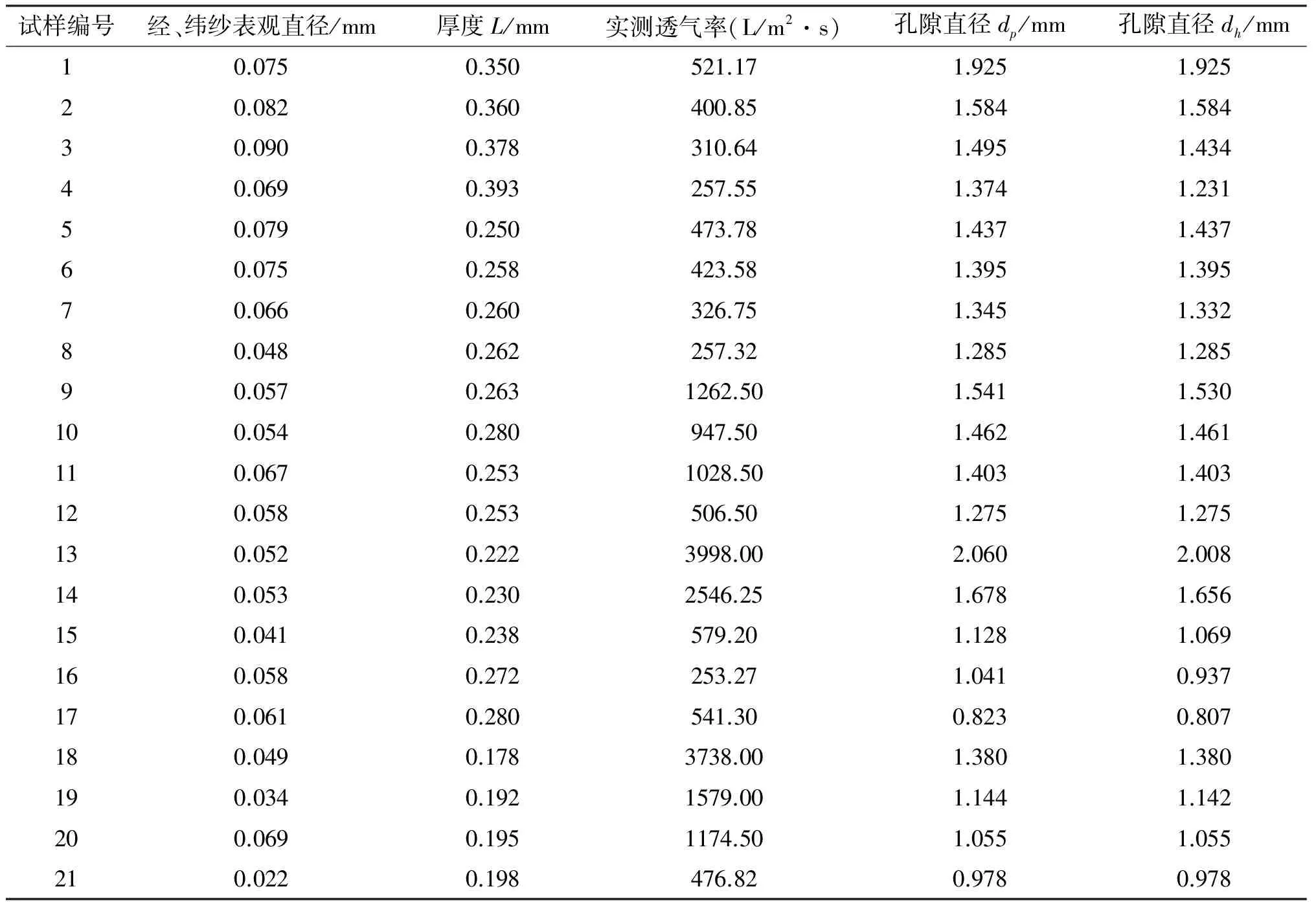
表2 织物测试数据及孔径计算结果

3 透气性预测计算公式构建

分别选取经纬纱线线密度为28.12、19.69、18.46、14.76tex和9.84tex的织物，改变织物经纬纱密度，计算出孔径dp、dh，绘制dp、dh与透气率之间的散点图。其结果如图2、图3。

通过观察所得散点图可知，随着织物纱线线密度的增大，透气率先增大后减小，说明织物透气性能大小不仅受织物经纬纱密度影响，同样也受织物纱线线密度等其他因素影响。在特定纱线线密度下，织物透气率随孔径的增大而增大，观察图2、图3可发现两者之间呈线性关系。变化规律同时适用于dp、dh。可见在纱线线密度确定的条件下，织物透气率大小可表示为，

图2 dp与透气率之间关系

图3 dh与透气率之间的关系

(4)

式(4)中：Ap表示透气率，d表示孔径dp或dh，K、B为待定参数。

相同纱线线密度下，对孔径和透气率之间线性关系进行线性拟合，得出在给定的纱线线密度下，织物孔径和透气率之间的函数关系式。图4是织物纱线线密度在14.76tex时，织物孔径dp与透气率之间的线性拟合。图5是织物纱线线密度在14.76tex时，织物孔径dh与透气率之间的线性拟合。

图4 dp与透气率之间拟合关系

图5 dh与透气率之间拟合关系

采用同种拟合方法，对其他纱线规格下的孔径与透气率之间进行数据拟合，得出在不同纱线规格下，孔径分别为dp、dh与透气率之间的函数关系，如表3，表4。

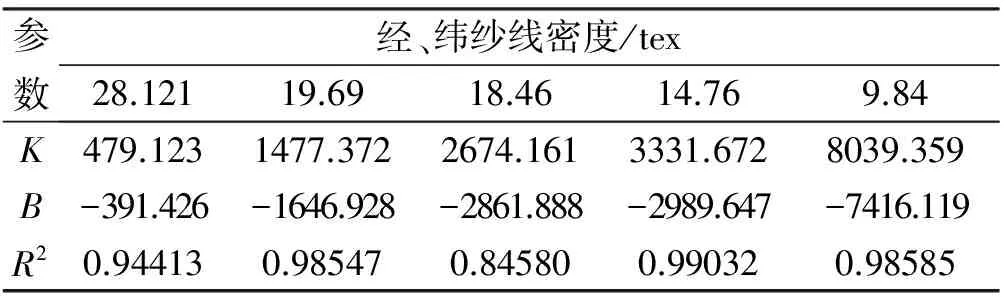
表3 孔径dp在不同线密度下对应的参数K、B值

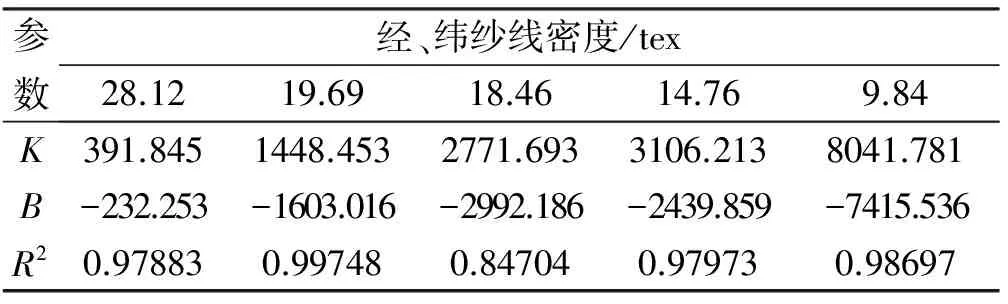
表4 孔径dh在不同线密度对应的参数K、B值

由表3、表4可发现，透气率计算公式中的参数K、B随织物纱线线密度变化而变化，绘制散点图，观察分析两者之间符合指数函数曲线，利用Origin8.0进行数据拟合，得出K、B与织物纱线线密度之间的函数关系。如图6、图7为孔径dp时参数K、B与线密度之间的拟合关系。

图6 线密度与参数K之间的拟合曲线

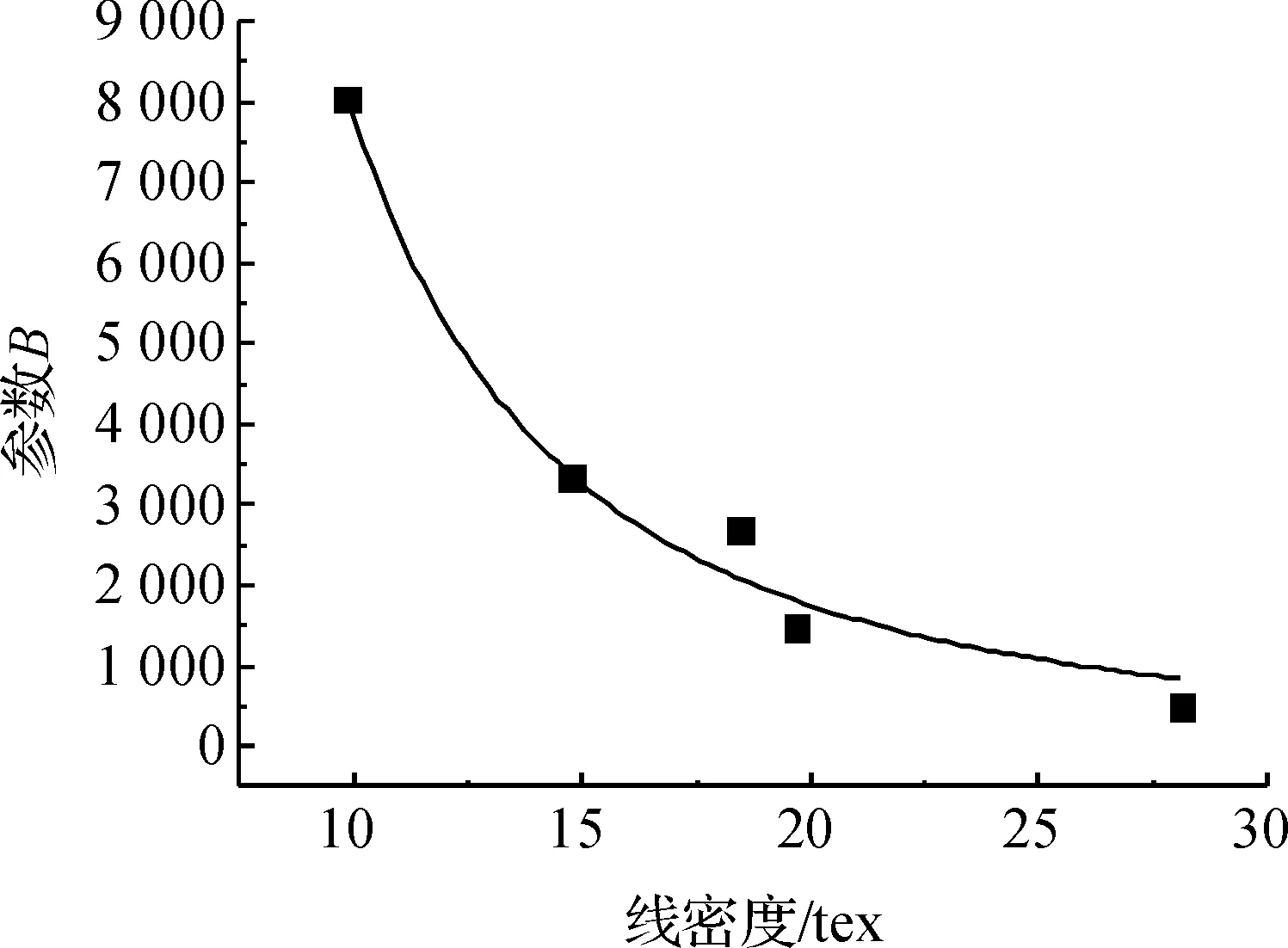
图7 线密度与参数B之间的拟合曲线

同样，在孔径dh的情况下，对纱线线密度和参数K、B之间分别绘制散点图。拟合纱线线密度与参数K、B之间的相关函数关系。分别将dp、dh所得参数K、B回代至式(4)中，得到透气率预测计算式如式(5)、式(6)。

Ap=114910T-2.15563dp-763859.013T-2.022697

(5)

Ap=1233480T-2.20088dh-998435.021T-2.14753

(6)

4 验 证

根据拟合所得织物透气率预测计算式，选取8块面料进行验证，与前面拟合样相同，计算孔径dp、dh,测量验证样透气率及厚度。参数见表6。

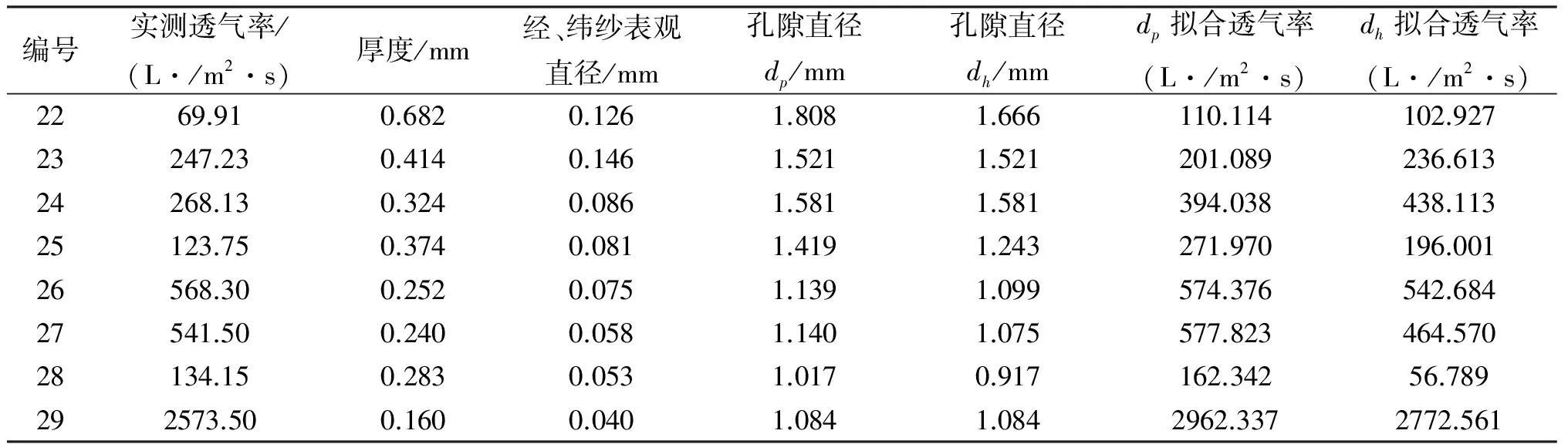
表6 验证样各项参数

将所得的计算值与实测值进行相关性分析，验证所得预测值的准确性。通过相关性分析可得孔径计算方法选取dp时，将拟合方程计算值与实测值之间进行相关性分析，其相关系数为0.9927。选取dh时，计算值与实测值之间相关系数为0.9952。

5 结 论

a) 使用两种计算方法计算织物孔径大小dp、dh，通过实验测试织物透气率。绘制织物孔径和透气率之间散点图，观察发现在线密度不变的情况下，织物透气率和孔径dp、dh呈线性相关。透气率和孔径之间计算公式中的参数K、B随织物纱线线密度增大而减小。

b) 利用软件拟合平纹全棉织物透气率预测计算式。所得拟合式用于平纹棉织物透气率计算，计算值与实测值之间相关系数可达到0.99以上。表明通过数据绘制散点图，分析相关参数与所求值之间的函数关系，有针对性进行数据拟合，该种方法用于织物的透气性预测具有较高的可行性。

c) 两种不同的孔径dp、dh用来拟合织物透气率预测公式，所得计算值和实测值之间相关系数分别为0.9927、0.9952。结果表明：对于平纹棉织物的透气率预测公式拟合，选用孔径dh时预测值与实测值之间相关性相对更高，在后期的平纹棉织物透气性预测研究中，选用孔径dh作为预测参数可行性更高。

[1] 俞月莉,张 丽,周 强,等.织物透气性测试方法标准之比较[J].纺织标准与质量,2011(4):21-25.

[2] Wang L Y , Mao L E.Valuation and prediction of wet comfort performance of knitted fabric underwear using artificial neural network [C]//3rd International Symposium of Textile Bioengineering and Informatics,2010:1335-1341.

[3] 田 丽,高 洪,葛 愿,等.基于RBF神经网络的织物透气性预测研究[J].自动化与仪器仪表,2006(5):6-8.

[4] 王 健,张晓丽,刘 陶.机织物透气性预测的投影寻踪回归模型[J].纺织学报,2011(8):47-49.

[5] 徐广标,王府梅.基于BP神经网络的精纺毛织物透气性能的预测[J].毛纺科技,2008(2):54-56.

[6] 曹建达.棉织物透气性能的BP神经网络预测研究[J].棉纺织技术,2004,31(11):19-21.

[7] Havlova M. Air permeability and costructional parameters of woven fabrics[J]. Fibres & Texties in Eastern Europe,2013,21(2):84-89.

[8] Kulichenko A V, Langenhove L V. The resistance to flow transmission of porous materials[J]. Journal Textile Institute, 1992,83(1):127-132.

[9] Zupin Z, Hladnik A, Dimitrovski K. Prediction of one-layer woven fabrics air permeability using porosity parameters[J].Texties Research Journal, 2011(2): 117-128.

[10] 邱茂伟,王府梅.机织物透气性能的预测研究[J].纺织学报，2005,26(4):73-75.

(责任编辑：许惠儿)

Prediction of Air Permeability of Cotton Fabrics

XUYaoyaoa,ZHULishaa,DULeia，ZOUFengyuana，b

(a.School of Fashion Design and Engineering; b.Zhejiang Garment Engineering Technology Research Center, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Two methods of calculation of the aperture were adopted to calculate thedpand thedh. Under particular yarn linear density, change rules between aperture and air permeability of fabrics were studied. Then, yarn linear density was changed to observe effects of changes in yarn linear density on air permeability of fabrics. Origin software was used to fit the relationship among air permeability, yarn linear density, weft and warp yarn density, aperturedpor aperturedh. The results show whendpand dh are used as fitting parameters, correlation coefficients of air permeability calculated according to the function and actual air permeability are 0.9927 and 0.9952, respectively. It thus can be seen that the fitting function can be used to predict air permeability of cotton fabrics. for aperture selection, prediction accuracy whendhis adopted is slightly higher than that whendpis adopted.

cotton fabric; fitting; air permeability; relevance

2014-09-10

纺织科学与工程重中之重一级学科2013年学生科研创新计划项目(11110031211202)

徐瑶瑶(1991—)，女，浙江衢州人，硕士研究生，主要从事服装人体工程与舒适性方面的研究。

邹奉元，E-mail:zfy166@zstu.edu.cn

TS195.644

A

1009-265X(2015)03-0026-05