基于TRMM数据提取降雨侵蚀力的校正方法——以蓟运河上游地域为例

靳秋桐,史明昌,†,张举涛,王珊,胡影

(1.北京林业大学水土保持学院,100083,北京；2.北京林业大学水土保持与荒漠化防治教育部重点实验室,100083,北京；3.北京地拓科技有限责任公司,100084,北京；4.高德软件有限公司,102200,北京)

基于TRMM数据提取降雨侵蚀力的校正方法
——以蓟运河上游地域为例

靳秋桐1,2,史明昌1,2,3†,张举涛1,2,王珊4,胡影3

(1.北京林业大学水土保持学院,100083,北京；2.北京林业大学水土保持与荒漠化防治教育部重点实验室,100083,北京；3.北京地拓科技有限责任公司,100084,北京；4.高德软件有限公司,102200,北京)

由于TRMM数据的时间分辨率较低,导致用TRMM数据计算某一区域指定时间段内的降雨侵蚀力存在较大的系统误差。为解决该问题提出通过统计研究区气象站实际降雨过程的数据,或者通过模拟研究区典型降雨过程,确定不同降雨过程中不同时间分辨率下降雨侵蚀力的差异程度,并以此对每一场降雨的降雨侵蚀力进行修正,进而校正指定时间段的降雨侵蚀力。为验证该方法的有效性,以蓟运河上游地区为研究区,在Matlab 2010b中对当地典型降雨过程进行模拟,计算当地不同时间分辨率下降雨侵蚀力差异程度,并利用典型降雨年份2008年的TRMM 3B42数据(0.25°×0.25°空间分辨率及3 h时间分辨率)通过ENVI-IDL语言程序进行校正计算。结果表明,经过校正后,研究区年降雨侵蚀力分布约为900～2 900 MJ·mm/(hm2·h)。该结果与这一地区多年平均降雨侵蚀力的量级及分布一致,说明该校正方法是一种切实可行的、能有效提高TRMM数据应用精度的方法；但是受TRMM数据空间分辨率的限制,该方法只适用于研究大中尺度区域降雨侵蚀力。

降雨侵蚀力；TRMM；系统误差；校正方法；蓟运河流域

近些年来全球气候变化导致极端天气频繁发生,我国很多地区旱涝灾害事件剧增,这加重了我国土壤侵蚀严重程度[1]。降雨是引起土壤侵蚀的重要因子,由降雨引起土壤侵蚀的潜在能力,即为降雨侵蚀力[2]5-8[3]。准确计算和评估降雨侵蚀力对各种土壤侵蚀模型的设计、模型精度的评价及准确定量预报土壤侵蚀工作都有重要的意义[4-6]。

降雨侵蚀力是用降雨的总动能和降雨强度估算的多年平均指标[2]50-51[6]。指定时间长度内,每场降雨的总动能E和对应场次最大降雨强度I的乘积EI的累计值作为该段时间内的降雨侵蚀力[3,7]。通常降雨资料从气象站点获取[8-9],但气象站点数量有限且分布不均,这使获取空间面域上的降雨侵蚀力分布情况变得极为困难[5,10]；此外,及时准确地评价和预报土壤侵蚀,需要及时准确的降雨数据去估算降雨侵蚀力,这些也是在现阶段技术条件下气象站难以满足的[9,11]。1997年11月美国和日本合作开发的全球第一颗搭载降水雷达的热带降雨观测卫星(Tropical Rainfall Measuring Mission,TRMM)发射成功,使获取准全球空间面域上的降雨分布即时数据成为现实,弥补了气象站观测数据的不足[11-13]。

学者们对TRMM数据在测算降雨强度和降雨量时的精度问题争议较大。C.M.Mannaerts等[14]认为TRMM数据的精度可用于大尺度空间降雨的研究；而T.Y.Pham[15]认为TRMM数据由于空间分辨率太低,并不能得到较为准确的降雨分布。研究区尺度越小,用TRMM数据计算结果的误差越大。TRMM数据不宜用于小尺度区域的研究,用其研究中等尺度空间范围内降雨侵蚀力也很少,通常只用其研究大尺度空间范围内的降雨量和降雨侵蚀力的分布[9-11,13,16]。现有TRMM数据计算降雨侵蚀力的方法分为2种,第1种是根据TRMM数据估算的降雨量结合研究区的经验公式间接计算,第2种是根据TRMM数据利用RUSLE的公式直接计算。第1种方法因计算过程简单,被广泛使用但是其可靠性差,误差不能估计。如Fan Jianrong等[9]选用经验公式利用TRMM计算的降雨量数据去估算降雨侵蚀力分布。第2种方法计算过程较为复杂,但是能够准确却反映研究区降雨侵蚀力变化趋势；为解决TRMM数据精度带来的误差,Zhu Qiang等[11]利用TRMM数据3 h统计的平均降雨强度和最大降雨强度代替30 min统计的平均降雨强度和最大降雨强度。A.Vrieling等[10,13,16]也简单认为2种时间分辨率下的最大降雨强度相等；但是这些处理方式与实际情况不符(详见第2节),从而降低了研究的可信度。

笔者基于以往利用TRMM数据计算降雨侵蚀力方法的研究,找到了一种有效提高TRMM数据在中等尺度上应用精度的方法,这既扩大TRMM数据的应用范围,且弥补部分地区地面气象观测的空白。此外,笔者在用TRMM数据计算降雨侵蚀力的方法基础上分析了该方法的系统误差,提出了一种可行的校正方法,并以蓟运河流域上游地区为研究区,利用典型降雨年份2008年的TRMM 3B42数据,对该校正方法进行了验证。

1 降雨侵蚀力计算方法

降雨强度是一个实时变化的物理量,时间分辨率越高,监测到的降雨强度变化越快,变化的幅度越大,统计到的降雨强度极值越大；反之,时间分辨率越低,变化幅度越小,统计到的极值越小。降雨侵蚀力是在平降雨强度和最大降雨强度的基础上计算得到。与降雨强度一样,降雨侵蚀力也受到时间分辨率的影响。为此RUSLE手册建议,用每30 min统计的平均降雨强度和最大降雨强度计算降雨侵蚀力[3,7],在降雨侵蚀力的研究计算中,只针对具有侵蚀性的降雨进行研究和计算(通常将降雨量＞12 mm的次降雨认定为侵蚀性降雨[17])。

1.1 地面气象站降雨资料计算降雨侵蚀力

地面气象站降雨监测数据的时间分辨率通常为30 min。RUSLE手册建议,利用这种数据计算降雨侵蚀力的公式[3,18]如下:

式中:R为年平均降雨侵蚀力,MJ·mm/(hm2·h)；n为计算R值得总年数；j为参与计算的年份序数；m为第j年内的暴雨次数；k为参与计算的次暴雨序数；E为次降雨总动能,MJ/hm2；I30为30 min时间分辨率资料统计的次降雨最大30 min降雨强度,mm/h；i30为30 min时间分辨率资料统计的次降雨平均降雨强度,mm/h；ΔV为对应时间段内的降雨量,mm。

1.2 TRMM数据计算降雨侵蚀力

TRMM3B42数据集由TRMM科学资料信息系统和TRMM办公室联合制作(在http:∥trmm.gsfc. nasa.gov/或 http:∥old-cdc.cma.gov.cn/免费获取),是基于红外亮温资料采用3B-42算法得到的准全球的降雨估量数据,其图像的一个像素点代表0.25°×0.25°经纬度范围,像素值为每3 h平均降雨强度资料,单位mm/h。即TRMM数据得到降雨强度资料的时间分辨率为180 min。

基于TRMM的降雨侵蚀力计算方法是根据RUSLE手册建议采用的降雨侵蚀力计算公式推导,采用TRMM 3B42中的3 h降雨量资料,筛除次降雨量小于12 mm的非侵蚀性降雨,采用K.G.Renard等[3]和Zhu Qiang等[11]的计算方法计算次降雨侵蚀力、月降雨侵蚀力和年降雨侵蚀力,计算公式如下:

式中:e为次降雨动能,MJ/(mm·hm2)；Rs为次降雨侵蚀力,MJ·mm/(hm2·h)；i180为180 min时间分辨率下的次降雨平均降雨强度,mm/h；I180为TRMM资料中的次降雨最大180 min降雨强度,mm/h；p为次降雨持续3 h段数,il为该次降雨第l个3 h段的平均降雨强度。计算时,将该次降雨中il的最大值作为次降雨最大180 min降雨强度,将il的平均值作为180 min时间分辨率下的次降雨平均降雨强度。

对于月降雨侵蚀力,则是将一个月内的次降雨侵蚀力叠加得到:

式中:Rm为月降雨侵蚀力,MJ·mm/(hm2·h)；q为该月次降雨的次数。

对于年降雨侵蚀力,则是将一年内的次降雨侵蚀力叠加而得到:

式中:Ry为年降雨侵蚀力,MJ·mm/(hm2·h)；r为该年次降雨的次数。

1.3 TRMM数据计算降雨侵蚀力分布

编写ENVI-IDL语言程序一次性读入研究范围内的TRMM 3B42数据,利用式(3)～(6)计算出每个网格(0.25°×0.25°)站点的降雨量以及降雨侵蚀力。这样得到的降雨侵蚀力可以表述大尺度上的降雨分布,但结果粗糙。通常利用地统计学方法对格网上的降雨侵蚀力进行克里格插值,得到更精细平滑的降雨侵蚀力分布。

为了准确构建插值模型,利用ArcGIS中探索性空间数据分析(ESDA)工具对数据进行检测及筛选。其中:使用自然间断点的分类符号方法对TRMM数据初步计算结果进行绘制和检查；利用趋势面分析任务,将经纬度坐标(x,y)与降雨侵蚀力的值(z)构成的点对投影在南北和东西2个平面上,得到的投影点分别进行趋势线回归拟合,得到南北和东西2个方向平面上的降雨侵蚀力变化趋势线,即得到趋势面分析图。根据趋势分析的结果决定克里金插值是否进行趋势剔除处理。

协同克里格方法可以给出有限区域内区域变量的最佳线性无偏估计量,在遥感图像处理中也得到了越来越广泛的应用[19]。因降雨受地形影响较大[20],所以结合研究区域的数字高程模型(DEM)可以对格网上降雨侵蚀力进行协同克里格插值。在对TRMM数据进行克里格插值之前,需要将上一节中计算出的每个网格的降雨侵蚀力值作为该网格中心点位置的降雨侵蚀力,然后进行插值[10-11,13,16]。

2 降雨侵蚀力计算方法的校正

2.1 TRMM数据获取降雨侵蚀力时的误差来源

由遥感影像得到的TRMM数据源计算的降雨侵蚀力结果必然存在一定程度的误差。该误差分为2类:随机性误差和系统性误差。随机性误差由TRMM卫星遥感获取数据时降雨强度大小及取样时间的随机性引起,也由不同尺度凸显的地学要素(地形、地貌及地理位置等)影响的随机性引起。随机性误差不可避免,尤其地学要素对降雨侵蚀力总体趋势的影响会随着尺度的缩小被逐步放大。系统性误差由TRMM卫星搭载的测雨雷达的精度水平、监测时间间隔,及TRMM数据计算降雨侵蚀力的计算方法差异导致。由设备精度带来的误差随着技术水平的改进可以提高,由计算方法带来的系统误差可以估计并消除。

利用不同时间分辨率气象站降雨资料得到的降雨侵蚀力大小不一样[8,18]。研究TRMM数据计算的降雨侵蚀力精度及误差值,需要选定评判的标准,以往研究中通常采用 30 min降雨资料作为基准[3,7]。因为气象站数据只是针对特定空间点的降雨数据,所以对于面域的降雨分布来说,气象站定点数据作为TRMM数据计算结果的基准并不合适；故不能对由随机性造成的误差进行准确的估计。笔者只分析由计算方法引起的系统误差。

2.2 不同分辨率数据计算降雨侵蚀力方法的差异

受TRMM 3B42数据时间分辨率3 h的限制,不能获取式(1)和式(2)中所需的30 min时间分辨率统计的次降雨最大降雨强度I30和平均降雨强度i30；因此,在利用TRMM数据计算降雨侵蚀力时,采用180 min分辨率下统计的次降雨平均降雨强度i180和最大降雨强度I180来替代较难获得的30 min时间分辨率统计的次降雨最大降雨强度I30和平均降雨强度i30,利用式(3)和式(4)来计算次降雨侵蚀力。

不同的计算方法应用于同一地区会存在不同(甚至相差数倍)的降雨侵蚀力值[6]。降雨量、历时及降雨时程(雨量随历时分配过程)的不同对一场降雨的降雨强度有显著的影响。对于一场历时恰好为30 min的侵蚀性降雨来说,如果在降雨开始时刻计时统计,最大降雨强度I30是I180的6倍,而平均降雨强度i30也是i180的6倍。由此可见,气象站数据和TRMM数据计算降雨侵蚀力所得结果的差异,其实质上是不同时间分辨率下(最大和平均)降雨强度的差异[18]。在这种情况下,确定30 min与180 min时间分辨率下降雨强度的关系是校正在TRMM数据提取降雨侵蚀力中系统误差的前提。

确定同一场降雨在不同时间分辨率下降雨强度之间关系的途径有2种:1)通过研究区气象站大量的实际降雨过程数据,统计推算出研究区不同类型降雨的降雨历时、降雨量和降雨强度之间的关系式；2)通过研究区域的暴雨强度公式并结合设计雨型,进行研究区不同典型降雨过程的时程分配,以这些时程分配统计出不同时间分辨率下不同类型降雨的降雨历时、降雨量和降雨强度之间的关系式[21][22]3-5[23]14-17。 显然,在缺少精细降雨资料的情况下,第二种途径更为可行。根据得到不同时间分辨率下降强度的关系,计算出对于同一场降雨不同时间分辨率下降雨侵蚀力之间的关系:

式中:μ为降雨侵蚀力差异系数；R30和R180分别为30 min和180 min时间分辨率降雨资料计算的次降雨侵蚀力,MJ/(mm·hm2)。

2.3 TRMM提取降雨侵蚀力校正方法

基于以上分析,对于1.2节中使用TRMM数据计算大中尺度区域的降雨侵蚀力的方法,提出了以下校正方法:

1)建立不同历时和不同降雨量的典型降雨过程降雨侵蚀力之间的关系表(μ值表)；

2)对于实际降雨,根据该场降雨的历时和降雨量,在步骤1得到的差异值表中找出对应的降雨侵蚀力差异值μ；

3)利用该差异值μ乘以TRMM数据计算的初步结果,得到每一场次降雨降雨侵蚀力的修正值R′s,

4)通过累加每日、每月、每年内的对应降雨场次的修正值,得到修正后日、月、年的降雨侵蚀力。

得到修正后的降雨侵蚀力之后,根据1.3节所述利用协同克里格插值计算降雨侵蚀力分布。

3 应用案例

3.1 研究区概况

蓟运河流域上游地区位于河海流域北部,东临滦河,西临潮白河,地跨北京、天津及河北3省市, E116°50′～118°15′,N39°45′～40°45′之间(图1)。蓟运河主要支流有泃河、州河,泃、州两支于天津市宝坻区九王庄汇流后称蓟运河。九王庄以上地区为蓟运河的主要汇水区域,即为蓟运河上游地区。该区域衔接燕山山脉与华北平原,其北部地区为起伏的中低山、丘陵地形,南部地区以平原区为主。该地区属于温带半湿润大陆性季风气候,季风气候显著。

3.2 数据来源

根据中国气象数据共享服务网年降水量数据,蓟运河上游地区所在的北京市、天津市和承德市2003—2013年的11年间的降水量相关性很强,且各市2008年的降雨量相当于其11年平均值(图2)；因此选取2008年为蓟运河上游地区的典型降雨年份,并以此计算蓟运河上游地区降雨侵蚀力分布特征和分析计算结果的精度及误差。

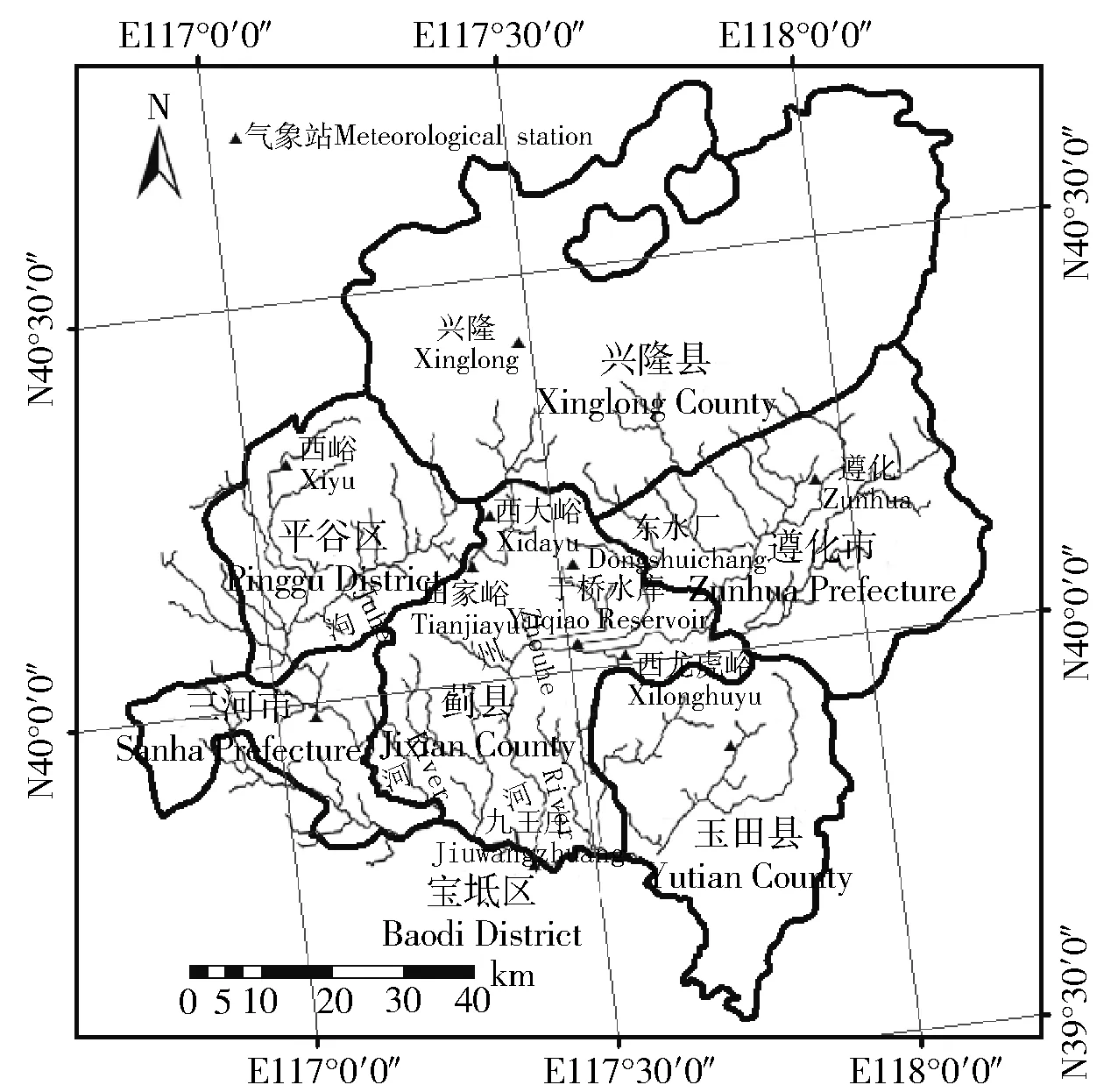
图1 研究区域及区内主要气象站点分布示意图Fig.1 Location of the study area with distribution of meteorological stations

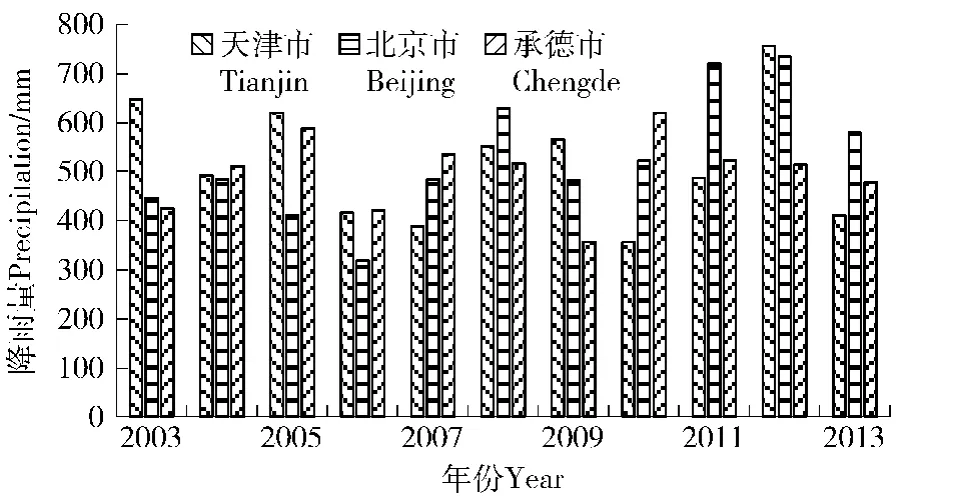
图2 天津市、北京市和承德市近10年间年降雨量分布Fig.2 Annual precipitation distribution of Tianjin,Beijing and Chengde in the recent decade

研究区降雨数据采用2008年的TRMM 3B42数据(数据获取见1.2节),在ArcGIS中裁剪范围在E116°26′57″～118°8′10″,N39°16′35″～40°47′33″的数据进行研究。

研究区数字高程(DEM)数据来自日本METI与美国NASA于2011年联合开发的ASTER GDEM数据(可在http:∥gdem.ersdac.jspacesystems.or.jp/ index.jsp注册下载)。选用DEM数据格式为Geo-TIFF,图像的空间分辨率为30 m。

3.3 蓟运河上游地区μ值计算

因缺少研究区以往精细降雨资料,采用设计典型降雨过程去计算蓟运河上游地区μ值表。典型降雨过程的设计需要确定雨型和暴雨强度公式。

国内外常用的雨型有芝加哥雨型、模式雨型、Huff雨型、三角形雨型、SCS雨型等等。各种雨型之间存在差异,目前还没有一种公认的雨型作为设计的依据[23]46-57。本研究区内,缺乏唐山及承德雨型的相关研究,而天津市区用Haff雨型的研究比较多,但天津市区属于海洋性气候,降雨过程与内陆有别,故不采用天津市的雨型公式。北京市降雨雨型多用芝加哥雨型或在其基础上改进的雨型,并结合北京市暴雨公式进行相关设计研究[21][22]20-21,笔者选用北京市用过的芝加哥雨型。

通过蓟运河上游地区暴雨强度公式结合常用的芝加哥雨型计算μ值表,但缺少蓟运河上游地区暴雨强度公式的研究和记载；而天津市相关暴雨强度公式是根据天津市区气象站资料求得[24]。天津市区临海,其降雨量受海洋影响较大,而蓟运河上游地区距其较远,且在内陆,地形地貌差距较大,选用天津市暴雨强度公式不合适；因此采用纬度相近、地理范围相互重叠、地形地貌相似的北京市第二暴雨分区的暴雨强度公式作为替代。笔者所用北京市第二区设计暴雨强度公式[21][22]3为

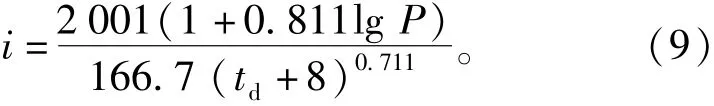
式中:i为平均降雨强度,mm/min；td为降雨历时, min；P为设计降雨重现期,a；在选定总降雨量下,迭代试算出P值。

降雨历程的分配使用芝加哥雨型,雨峰系数r取0.25,则峰前时间序列i(tb)和峰后时间序列i (tc)分别用如下公式[21,25]计算:

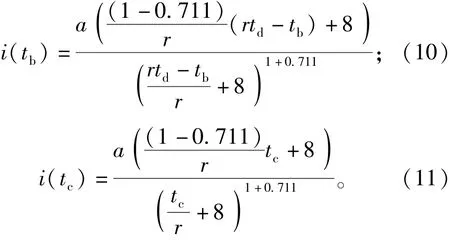
为了简化运算,在校正降雨侵蚀力时,不考虑每场降雨的降雨量大小不同,只考虑侵蚀性降雨的降雨历时变化。选取降雨量为25 mm(国家气象局规定的中雨和大雨的分界线),历时分别为0.5、1、2、3、4、5、6 h的7场降雨,利用式(8)～(11)在Matlab 2010b中合成降雨过程,模拟的步长为1 min。

对上述拟合所得不同降雨过程曲线进行统计计算,以降雨开始时刻为统计起点,得到30 min与180 min分辨率下最大、平均降雨强度及对应的降雨侵蚀力(表1)。

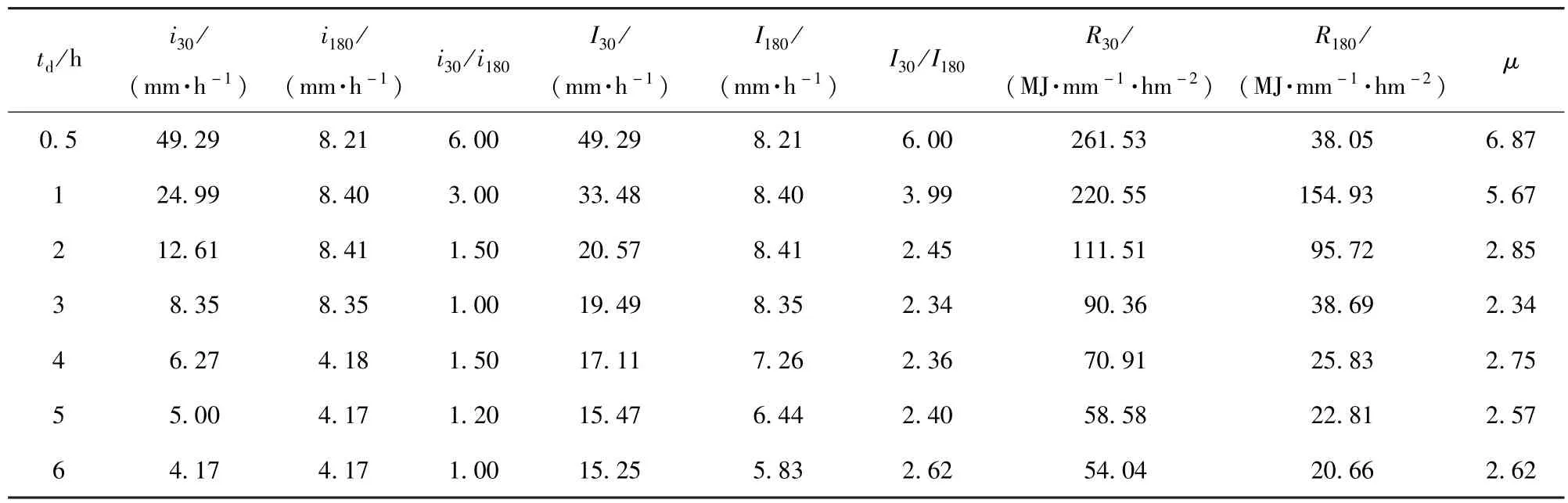
表1 不同降雨过程特征物理量及μ值Tab.1 Characteristics of physical quantities including μ value in different rainfall processes

平均降雨强度随时间分辨率的差异随降雨历时而不同(表1),但以此计算降雨动能E相差只有16.5%左右,这相比于最大降雨强度随时间分辨率的差异较小,此结果与前人研究结果[26]一致。最大降雨强度随时间分辨率的差异均在135%以上,即I30≈2.35I180,这表明最大降雨强度受时间分辨率的影响程度与降雨历时的关系不紧密。同时证明Zhu Qiang等[11]和 A.Vrieling等[10,16]研究时简单认为I30=I180是不对的。

TRMM数据只能反映出每3 h内是否发生降雨,降雨持续了几个3 h段,并能得出实际降雨的历时。根据李建等[27]研究,20世纪90年代以后北京市降雨以6 h以下降雨为主,且贡献最大的为2～4 h降雨。并且笔者通过TRMM数据发现＞6 h的降雨非常少,只占到6.7%左右,没有连续＞9 h的降雨。另外,根据表1,随着降雨历时的增加,μ值变化幅度较小。因此我们采用了2、4、6 h的降雨代表＜3 h、介于3～6 h的降雨、＞6 h的降雨。即校正时,历时≤3 h的降雨,其降雨侵蚀力乘以μ2h(2.85)；降雨介于3～6 h的降雨,其降雨侵蚀力乘以 μ4h(2.75)；历时＞6 h的降雨,其降雨侵蚀力乘以μ6h(2.62)。本文中所模拟的2、4、6 h的降雨时程过程如图3所示。

3.4 结果与分析

表2 蓟运河上游地区7个县市的主气象站点所在网格的降雨侵蚀力校正前后对比Tab.2 Rainfall erosivity on grids with main meteorological sites on seven counties of Jiyun River upriver before and after the calibration

3.4.1 降雨侵蚀力校正前后数据对比 表2说明,对每场降雨的降雨侵蚀力经过校正之后,不同网格处累计得到2008年降雨侵蚀力的值均提高了2倍以上,使研究区2008年的降雨侵蚀力的量级与多年平均降雨侵蚀力[28-29]一致；故这样的校正显著提高了TRMM数据使用时的精度。

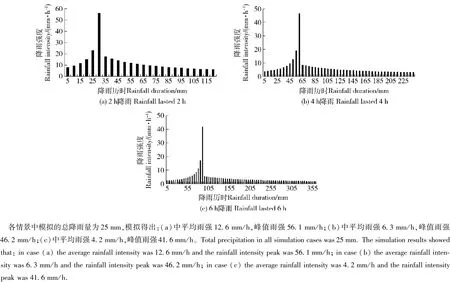
图3 设计25 mm降雨量不同历时降雨过程Fig.3 Rainfall process in different designed durations at precipitation of 25 mm

3.4.2 降雨侵蚀力分布趋势 图4表明较大的侵蚀力出现在该区域南部地区,中部地区降雨侵蚀力居中,北部地区较小,即该地区降雨侵蚀力自东南到西北逐渐减弱的趋势。图5中可以直观地看出,东西、南北方向变化趋势近似。自东向西,数据点分布较为分散,东西方向拟合趋势线有微弱的先升再降的趋势；而南北方向拟合趋势线数据点自南向北有微弱的减弱趋势。以上2方向上的趋势与蓟运河上游地区地形相符合,北部山势影响山前平原降雨比较多。

3.4.3 降雨侵蚀力插值结果及分析 协同克里格方法是根据半变异函数分析所提供的变量空间自相关程度的信息来进行插值,插值准确程度与半变异函数拟合的好坏直接相关[19]。表3示出,指数模型在平均值、标准平均值、标准均方根3个指标上是误差最低。在均方根指标上,指数模型的结果与该指标最低值差异不大。只有在平均标准误差上,指数模型的结果高于其他模型。综合其他2个模型的误差结果来看,指数模型模拟效果最好,故本研究采用指数模型进行后面的插值参数改进。

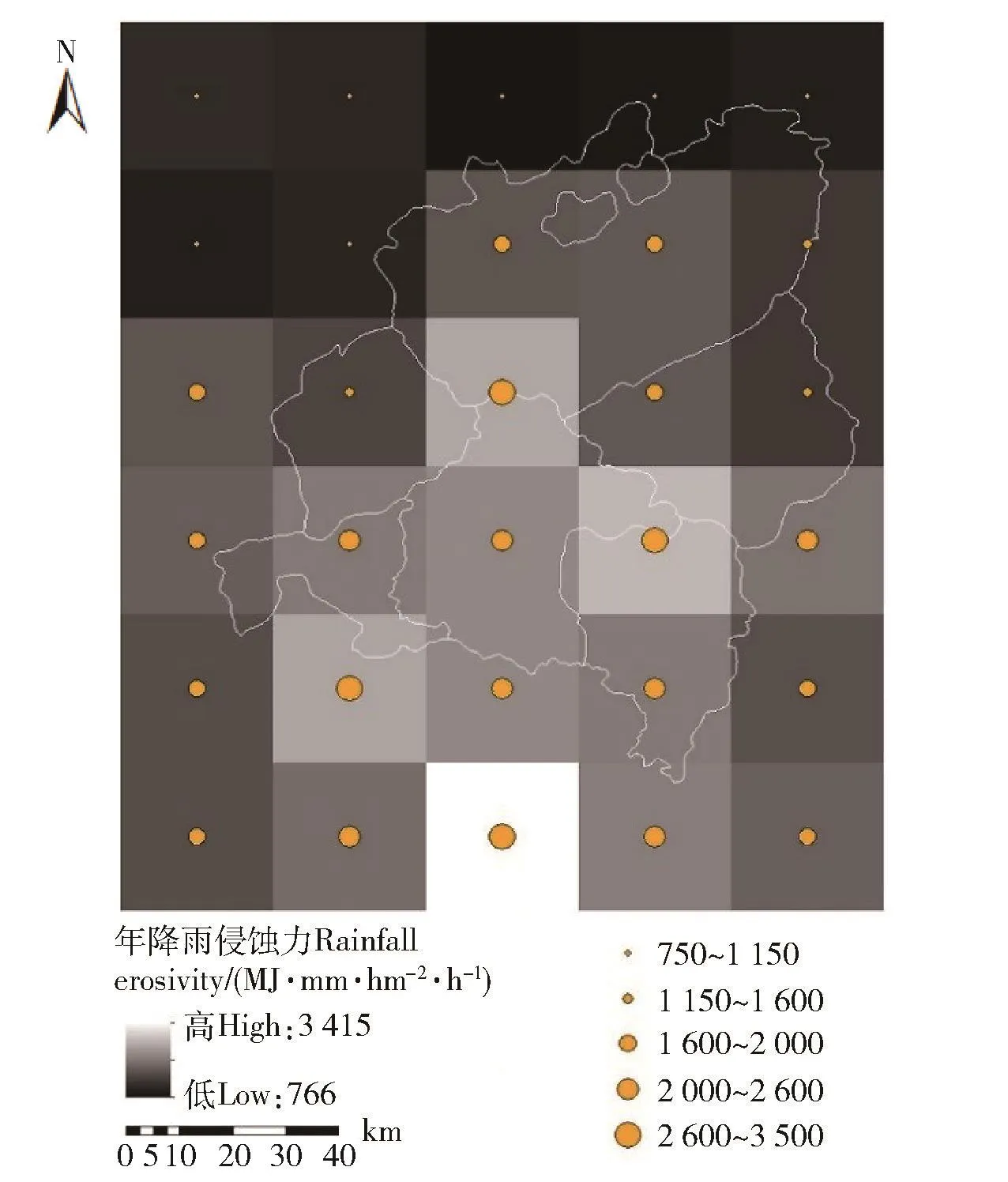
图4 2008年降雨侵蚀力自然间断点分类符号图Fig.4 Classification symbols of natural discontinuities of rainfall erosivity in 2008

块金值与基台值的比值C0/(C0+C)称为块金效应,它表示随机部分引起的空间变异占系统总变异的比例[30]。如果该比值较低,表明结构性因素引起的空间变异起主要作用；如果该值较高,说明随机部分引起的空间变异起主要作用。通常认为:块金效应＜25%,空间相关性强；25%～75%之间,空间相关性中等；＞75%,空间相关性弱。本文采用指数模型计算的块金值为0,基台值为72 241,块金效应＜25%,表明TRMM像素值具有强烈的空间相关性,其结构性因素引起的空间变异起主要作用。

图5 2008年降雨侵蚀力趋势面分析Fig.5 Trend surface analysis of rainfall erosivity in 2008

依据拟合的半变异函数模型协同DEM进行克里格插值。研究区年降雨侵蚀力分布约为900～2 900 MJ·mm/(hm2·h)。图6表明,该区域降雨侵蚀力东南到西北逐渐减弱,南部地区大于北部地区,该变化趋势和章文波等[28]、刘斌涛等[29]研究结果一致。

表3 不同半变异模型的误差评价结果Tab.3 Error analysis of different fitting models of semi-variance function

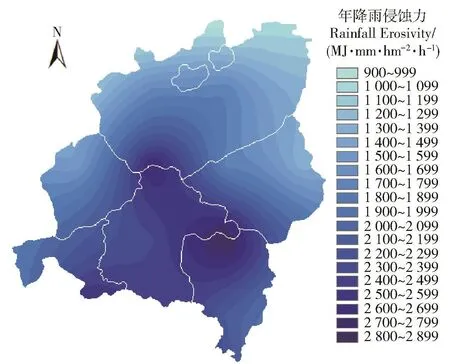
图6 蓟运河上游各县域降雨侵蚀力分布图Fig.6 Rainfall erosivity distribution on the upriver counties of Jiyun River

4 结论与讨论

以典型降雨年份2008年蓟运河上游地区的降雨侵蚀力计算为研究案例,结果显示校正后的降雨侵蚀力接近了多年平均降雨侵蚀力的量级及分布。这说明通过确定不同降雨过程中不同时间分辨率下降雨侵蚀力差异的μ值表,并以此对每一场降雨进行修正,进而减少TRMM数据计算降雨侵蚀力是系统误差的方法,是一种切实可行的、有效提高TRMM应用结果精度的方法。

受到TRMM数据时空分辨率的影响,该方法只能用于大中尺度区域降雨侵蚀力的研究,不能用于小尺度区域的研究。该方法并不限制如何选择降雨雨型和下垫面条件的影响。降雨雨型不同选择,会使影响校正结果的精度,但是这种影响远比未校正之前的误差小。下垫面条件引起的误差属于随机性误差,在现有研究的基础上,暂时无法估计下垫面条件的影响规律和引起误差大小。

确定不同降水过程对应的μ值是应用该方法的前提和基础。这一步骤需要以实际降雨过程数据进行统计分析为基础,或者以更多典型降水过程的模拟数据为基础。由于各地降雨量不同,降雨过程随机变化,应用该方法是需要因地制宜,确定出适合当地的μ值表。当然在误差允许的条件下,也可以制订各气候区或降雨类型区统一的μ值表,方便以后随时调取使用。从本文案例的校正过程来看,影响校正结果效果的因素有雨型确定的方法、雨型种类、不同降雨历时的降雨所占的比例、不同降雨历时及不同降雨量的降雨对应的雨型种类等。追求更高精度的校正效果时,须对这些问题进行深入的研究,这也是今后进一步研究和改进完善该校正方法途径。

[1] 王占礼.中国土壤侵蚀影响因素及其危害分析[J].农业工程学报,2000,16(4):32- 36

[2] Wischmeier W H,Smith D D.Predicting rainfall erosion losses:a guide to conservation planning[J].Agriculture Handbook 537,1978:5- 8,50- 51

[3] Renard K G,Foster G R,Weesies G A,et al.Predicting soil erosion by water:aguide to conservation planning with the revised universal soil loss equation(RUSLE) [J].Agriculture Handbook 703,1997:22- 38

[4] 叶芝苗,刘宝元,章大波,等.北京市降雨侵蚀力及其空间分布[J].中国水土保持科学,2003,1(1): 16- 20

[5] 章文波,付金生.不同类型雨量资料估算降雨侵蚀力[J].资源科学,2003,25(1):35- 41

[6] 卜兆宏,董勤瑞,周伏建,等.降雨侵蚀力因子新算法的初步研究[J].土壤学报,1992,29(4):408- 417

[7] Yu Baofu,Rosewell C J.A robust estimator of the R-factor for the Universal Soil Loss Equation[J].Transactions of the ASAE,1996,39(2):559- 561

[8] 章文波,谢云,刘宝元.用雨量和雨强计算次降雨侵蚀力[J].地理研究,2002,21(3):384- 390

[9] Fan Jianrong,Chen Yang,Yan Dong,et al.Characteristics of rainfall erosivity based on tropical rainfall measuring mission data in Tibet,China[J].Journal of Mountain Science,2013,10(6):1008- 1017

[10]Vrieling A,Hoedjes J C B,van der Velde M.Towards large-scale monitoring of soil erosion in Africa:Accounting for the dynamics of rainfall erosivity[J].Global and Planetary Change,2014,115:33- 43

[11]Zhu Qiang,Chen Xiuwan,Fan Qixiang,et al.A new procedure to estimate the rainfall erosivity factor based on Tropical Rainfall Measuring Mission(TRMM)data[J]. Science China Technological Sciences,2011,54(9): 2437- 2445

[12]Kummerow C,Barnes W,Kozu T,et al.The tropical rainfall measuring mission(TRMM)sensor package[J]. Journal of atmospheric and oceanic technology,1998,15 (3):809- 817

[13]Vrieling A,Sterk G,de Jong S M.Satellite-based estimation of rainfall erosivity for Africa[J].Journal of hydrology,2010,395(3):235- 241

[14]Mannaerts C M,Saavedra C P.Regional scale erosion modeling and monitoring using remotely sensed data: some spatial data scale issues[C]∥Proceedings of the international symposium on 25 years of assessment of erosion.Ghent,Belgium:Ghent University,2003:433- 440

[15]Pham T Y.Soil erosion risk modeling within upland landscapes in Vietnam using remotely sensed data and the RUSLE model[D].Nova Scotia:Dalhousie University, 2008:79- 84

[16]Vrieling A,de Jong S M,Sterk G,et al.Timing of erosion and satellite data:a multi-resolution approach to soil erosion risk mapping[J].International Journal of Applied Earth Observation and Geoinformation,2008,10, 267- 281

[17]Xie Yun,Liu Baoyuan,Nearing M A.Practical thresholds for separating erosive and non-erosive storms[J]. Transactions of the ASAE,2002,45(6):1843- 1847

[18]Yin Shuiqing,Xie Yun,Nearing M A,et al.Estimation of rainfall erosivity using 5-to 60-minute fixed-interval rainfall data from China[J].Catena,2007,70(3): 306- 312

[19]冯益明,雷相东,陆元昌.应用空间统计学理论解译遥感影像信息“缺失”区[J].遥感学报,2004,8(4): 317- 322

[20]傅抱璞.地形和海拔高度对降水的影响[J].地理学报,1992,59(4):302- 314

[21]张大伟,赵冬泉,陈吉宁,等.芝加哥降雨过程线模型在排水系统模拟中的应用[J].给水排水,2008,34 (增刊2):354- 357

[22]北京市城市规划设计研究院.城市雨水系统规划设计暴雨径流计算标准:DB11/T 969—2013[S].北京:中国计划出版社,2013:3- 5,20- 21

[23]范泽华.天津市降雨趋势分析及设计暴雨研究[D].天津:天津大学,2012:14- 17,46- 57

[24]黄津辉,向文艳,户超,等.天津市设计暴雨方法比较及公式修正[J].天津大学学报,2013,46(4): 354- 360

[25]Keifer C J,Chu H H.Synthetic storm pattern for drainage design[J].Journal of the hydraulics division,1957,83 (4):1- 25

[26]殷水清,谢云,王春刚.用小时降雨资料估算降雨侵蚀力的方法[J].地理研究,2007,26(3):541- 547

[27]李建,宇如聪,王建捷.北京市夏季降水的日变化特征[J].科学通报,2008,53(7):829- 832

[28]章文波,谢云,刘宝元.中国降雨侵蚀力空间变化特征[J].山地学报,2003,21(1):33- 40

[29]刘斌涛,陶和平,宋春风,等.1960—2009年中国降雨侵蚀力的时空变化趋势[J].地理研究,2013,32(2): 245- 256

[30]Schabenberger O,Pierce F J.Contemporary statistical models for the plant and soil sciences[M].Boca Ration: CRC press,2002:563- 599

(责任编辑:宋如华)

Calibration of rainfall erosivity calculation based on TRMM data: A case study of the upriver basin of Jiyun River,North China

Jin Qiutong1,2,Shi Mingchang1,2,3,Zhang Jutao1,2,Wang Shan4,Hu Ying3
(1.School of Soil and Water Conservation,Beijing Forestry University,100083,Beijing,China；2.Key Lab.of Soil&Water Conservation and Desertification Combating,Beijing Forestry University,Ministry of Education,100083,Beijing,China；3.Beijing Datum Science and Technology Development Co.,Ltd.,100084,Beijing,China；4.AutoNavi Software Co.,Ltd.,102200,Beijing,China)

The low temporal resolution of TRMM data could cause systematic errors in the rainfall erosivity calculation within the specified time period.For this reason,we propose a method of calibration in order to reduce the errors in this paper.Firstly,a relationship table of rainfall erosivity at different events and duration with typical rainfall process is established with historical rainfall data or numerical simulation；then,the corresponding difference is calculated from the above table based on the precipitation and duration of each rainfall in the study area；afterwards,the adjusted value of rainfall erosivity in each rainfall is calculated by multiplying the figure found in the pervious step by the original value of rainfall erosivity correspondingly；finally,the calibrated value of daily,monthly or yearly rainfall erosivity isobtained by adding daily, monthly oryearly adjusted value ofrainfallerosivity correspondingly.To verify the effectiveness of this calibration method,the typical rainfall process in the study area,the upriver regions of Jiyun River,was simulated within Matlab 2010b to obtain therelationship table,and then the rainfall erosivity in the study area was calculated using TRMM 3B42 data in 2008 with the spatial resolution of 0.25°×0.25°and the time resolution of 3 h.The calculation was conducted in the ENVI-IDL Language program and calibrated by the relationship table.The results showed that:the rainfall erosivity in the upriver of Jiyun River ranged from 900 to 2 900 MJ·mm/(hm2· h)with the highest values in central area,followed by southern and northern parts,which was consistent with the local average annual values and distribution of rainfall erosivity.The results confirm that this method can effectively improve the precision of TRMM data's application.Due to the limitation of spatial resolution of TRMM data,this calibration method is only applied in the rainfall erosivity calculation at large and middle scales.In order to improve the precision of this calibration method,the typical rainfall process,rain type design and distribution of rainfall duration should be detailed.

rainfall erosivity；TRMM；systematic error；calibration method；Jiyun River

S157.1

A

1672-3007(2015)04-0094-09

2014- 11- 15

2015- 05- 03

项目名称:林业公益性行业科研专项经费项目课题“基于生态安全的水土保持措施空间配置技术”(201404209)

靳秋桐(1990—),男,硕士研究生。主要研究方向:3S技术集成与系统开发。E-mail:jinqiutong@bjfu.edu.cn

†通信作者简介:史明昌(1969—),男,博士,教授。主要研究方向:地理信息科学。E-mail:shimc@bjfu.edu.cn