改进ERTS平滑算法在位置跟踪中的应用研究
2015-06-15薛永胜霍建文
薛永胜 张 华 霍建文
(西南科技大学信息工程学院,四川 绵阳 621010)
改进ERTS平滑算法在位置跟踪中的应用研究
薛永胜 张 华 霍建文
(西南科技大学信息工程学院,四川 绵阳 621010)
针对标准ERTS平滑算法在位置和姿态估计中计算复杂、效率低、精度不高等问题,提出了利用奇异值分解法改进ERTS平滑算法优化位置和姿态数据的新方法。对系统采集到的位置和姿态信息进行前向扩展卡尔曼滤波,降低系统噪声的初步影响;对滤波后的均方误差阵进行奇异值分解,并降低后向递推增益和预测值计算量,提高了预测精度,有效增强了系统的抗干扰性和稳定性。Turtlebot移动机器人平台的试验效果证明该算法在位置和姿态估计中的高效性和稳定性。
扩展卡尔曼滤波 奇异值分解法 最优平滑算法 最优估计 位置跟踪
0 引言
精确、稳定的位置和姿态测算是移动机器人自主导航的核心课题之一。在诸多移动机器人位置和姿态定位算法中,预测、滤波和平滑三类最优估计[1]是提升移动机器人位姿受信息信噪比的有效方法,可为控制系统提供更精准、稳定的位置和姿态参数。
相对于滤波估计而言,平滑估计能够获得优于滤波的估计精度。平滑估计一般可分为固定点平滑、固定滞后平滑和固定区间平滑。其中,固定区间平滑的应用范围最为广泛,但固定区间平滑估计在后向递推计算中,需要进行协方差阵的求逆运算和两正定矩阵的相减运算,因此存在计算效率低和数值稳定性差的问题[1]。为解决这些问题,本文介绍一种改进的ERTS定区间平滑算法。
1 ERTS平滑算法
为保证移动机器人在移动过程中传感器提供的位置和姿态数据稳定可靠,实际引入了ERTS平滑算法削弱噪声对系统的影响。该算法对位置的姿态数据先进行EKF滤波,之后采用RTS平滑算法对数据进行最优平滑优化。系统框图如图1所示。

图1 系统框图
1.1 前向EKF滤波器
扩展卡尔曼滤波器于20世纪60年代提出,是一种历史悠久、应用广泛的非线性高斯次优滤波算法。该算法在卡尔曼滤波算法的基本框架上,通过对非线性函数的泰勒展开式进行一阶线性化截断,并以此近似非线性状态后验均值和协方差[2]。常用的非线性离散随机系统模型如下。
xk+1=f[x(k),u(k)]+ω(t)
(1)
(2)

将系统方程进行线性化[2]表示:
(3)
(4)

结合文献[2]~[3]中离散EKF滤波器的实现步骤,首先初始化滤波器,即当k=0时,有:
(5)
(6)
当K=1,2,…时,通过迭代运算估计各时刻目标的状态向量:
xk+1|k=f[x(k,k),u(k)]
(7)
Pk+1|k=JPk|kJT+Qk
(8)
(9)
(10)
(11)
xk+1|k+1=xk+1|k+Wk+1ϑk+1
(12)
(13)
相对传统的低通滤波器和卡尔曼滤波器,扩展卡尔曼滤波器不仅避免了状态方程线性化过程中带来的误差和不稳定影响,而且其具有自适应性的反馈增益矩阵,使得系统偏差在统计意义上达到最小,使系统能同时保证稳定性和响应速度[4]。
1.2RTS平滑算法
RTS平滑算法原理如图2所示。

图2 RTS平滑算法原理图
RTS平滑算法是一种利用某一时间区间内的所有量测信息对所有状态进行估计的离线处理算法。它能够获得优于滤波的估计精度[1,5],广泛应用于声音信号处理、目标跟踪和导航制导等领域[1,6-9]。该算法包括前向滤波和后向递推两个部分[1]。
图2中,上标“+”和“-”分别表示滤波的更新过程和预测过程;“F”和“S”分别表示前向滤波过程和后向递推平滑过程。前向滤波过程利用固定时间区间[0N]内所有采样值进行EKF滤波,并存储式(7)~(13)中的状态估计xk+1|k+1、估计均方差误差阵Pk+1|k+1和预测均方差误差阵Pk+1|k。后向递推公式[15]如下:
xk|N=xk+KS(xk+1|N-xk+1|k)
(14)
(15)
其中后向递推的平滑增益矩阵为:
(16)
1.3 算法改进
由于RTS算法中存在大量(n×n)矩阵相乘,为减少运算过程的存储和计算量,采用可靠的矩阵分解算法奇异值分解法[5]对Pk|N和Pk+1|N进行定义,得:
(17)
(18)
定义Mk满足:
(19)
将上式带入式(16)化简为:
(20)
为进行奇异值分解运算,将Mk求逆得:
(21)

(22)
对上式两边分别左乘各自转置阵后得到:
(23)
由式(20)和式(22)得到:
uk=V″kDk=(D″k)-1
(24)
同理可实现式(17)的奇异值分解运算,即:
uk|N=V″kDk|N=D″k
(25)
将式(23)和式(24)带入式(17)可得改进后的后向递推的平滑增益矩阵:
(26)
由式(23)~(25)及式(15)组成了最优RTS平滑算法,而配合前向EKF滤波过程产生的状态估计和误差矩阵即为本文改进的ERTS平滑算法。
2 应用及仿真分析
本文研究的移动机器人模型是基于两轮驱动的Turtlebot移动机器人,其位姿传感器型号及参数如表1所示。其中,ticks/enc表示每圈脉冲数。

表1 Turtlebot部分传感器参数
L3G4200D具有功耗低、精度高、使用灵活的特点,实际移动中仅用单轴进行航向参数测量;编码器精度高、体积小,其作为位置反馈的重要设备。为实现对移动机器人的位置跟踪控制,对机器人模型进行简化,如图3所示。

图3 Turtlebot机器人简化模型

(27)
其中D为小车前后轮间的间距。为了实现位置跟踪控制系统的闭环控制,控制系统加入陀螺仪和编码器对系统运动状态进行测量,其距离ri和偏转角度θi测量方程为:
(28)
式中:x、y为当前移动机器人本体在的坐标;xi、yi为上一次移动机器人本体的坐标。
设置采样周期T=10ms,Wk为[-1.0,1.0]的白噪声,vk为[-0.02,0.02]的白噪声信号,设角度跟踪输出指令为sint,t=kT,仿真时间10s,在软件MatlabR2012a进行系统仿真。
2.1 结果比较
为验证RTS平滑算法应用到目标跟踪的有效性,选取分段数N=10,结合文献[10]~[12]中的标准ERTS平滑算法和EKF滤波器进行输出效果对比,如图4所示。

图4 不同算法跟踪比较
由图4可见,单独的EKF滤波器效果在估计上存在较大波动,综合RTS平滑算法后在数据最优估计上更加平滑,有效削弱了噪声的影响。不同算法的跟踪误差曲线如图5所示。

图5 不同算法跟踪误差比较
三种算法在Matlab R2012a环境下的计算时间和误差对比如表2所示。

表2 不同平滑器算法性能比较
由表2分析知,三种算法均能有效地抑制噪声信号。单独的EKF滤波器波动较大。标准的ERTS平滑算法在EKF基础上添加了RTS平滑算法,多耗费0.118 s,精度提高52.0%,改进后的ERTS平滑算法定位精度相较于其他两者分别提高了54.6%、13.6%,并且在接近EKF的计算耗时内大幅提升了系统的精度和稳定性。将本文改进算法应用到Turtlebot机器人本体上,大大提高了其位置跟踪的精确度,验证结果如表3所示。
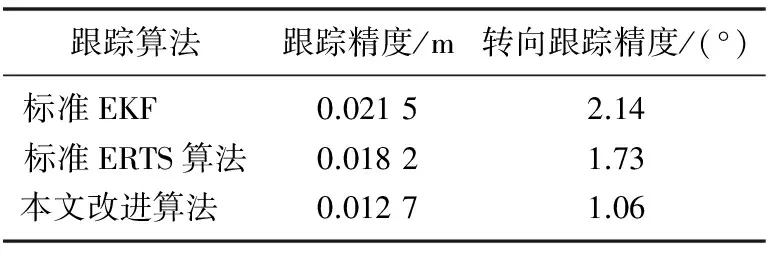
表3 Turtlebot机器人平台算法验证结果
2.2 抗干扰分析
由于控制系统中总存在着干扰和噪声,现代控制对系统的鲁棒性要求较高。为验证滤波器的抗干扰能力,将测量噪声和系统噪声均增强2倍,分别对标准ERTS和本文改进算法进行跟踪效果验证,结果如图6所示。

图6 增强Wk和vk后的跟踪结果
由图6分析可知,系统在噪声干扰下改进的ERTS平滑算法可以较好地稳定系统的输出,提高系统的跟踪精度。
3 结束语
本文采用奇异值分解法对标准的ERTS平滑算法进行化简改进,以获得移动机器人位置和姿态的最优估计值,实现精准导航定位。
文中利用Turtlebot移动机器人平台采集到的位置和姿态信息进行前向扩展卡尔曼滤波器初步滤波后,通过奇异值分解法化简的RTS平滑算法获得位置和姿态最优估计。仿真结果和试验证明该算法比单独的扩展卡尔曼滤波器和标准ERTS平滑算法具有更好的精确性和抗干扰能力。
[1] 宫晓琳,张蓉,房建成.固定区间平滑算法及其在组合导航系统中的应用[J].中国惯性技术学报,2012,20(6):687-693.
[2] Jetto L,Longhi S.Development and experimental validation of an adaptive extended kalman filter for the localization of mobile robots[C]//IEEE Transactions and Automation on Robotics,2009:143-150.
[3] Zhu Jihua,Zheng Nanning,Yuan Zejian,et al.A SLAM algorithm based on the central difference kalman filter[C]//Intelligent Vehicles Symposium,IEEE,2009:123-128.
[4] Zhang Haitao,Rong Jian,Zhong Xiaochun.The performance comparison and algorithm analysis of first/second order EKF and smoother for GPS/DR navigation[C]//11th IEEE International Conference on Communication Technology,2008:432-437.
[5] Sarkka S,Viikari V,Huusko M,et al.Phase-based UHF RFID tracking with nonlinear kalman filtering and smoothing[J].IEEE Sensors Journal,2012,12(5):904-910.
[6] Nassar S.Improving the inertial navigation system(INS) error model for INS and INS/DGPS applications[D].Alberta:University of Calgary,2003.
[7] 秦永元.惯性导航[M].北京:科学出版社,2005:10-230.
[8] Lei Xuan,Yang Jing.Application of RTS optimal smoothing algorithm in satellite attitude determination[C]//2011 2nd International Conference on Intelligent Control and Information Proceedings,2011:978-982.
[9] Nassar S,Liu Hang,El-Sheimy N.Two-Filter smoothing for accurate ins-gps land-vehicle navigation in urban centers[J].IEEE Trans.on Vehicular Technology,2010,59(9):4256-4267.
[10]于翔川.基于非线性滤波的目标跟踪算法研究[D].西安:西安电子科技大学,2009.
[11]Razali S,Watanabe K,Maeyama S,et al.An unscented rauch-tung-striebelsmoother for a bearing only tracking problem[C]//2010 Int.Conf.on ICCAS,2010:1281-1286.
[12]Simo Sarkka.Unscented rauch-tung-striebelsmoother[J].IEEE Trans.on Automatic Control,2008,53(3):845-849.
Application Research on the Improved ERTS Smoothing Algorithm in Position Tracking
To overcome the disadvantages of standard ERTS smoothing algorithm in position and attitude estimation, e.g., complexity, low efficiency, and poor precision, etc., the new improved ERTS smoothing algorithm by adopting singularity valve decomposition is proposed for optimizing position and attitude data. After forward extended Karman filtering for the information of position and attitude collected in the system, the initial impact ofthe system noise is reduced; the singularity value decomposition is conducted for the MSE matrix after filtering, thus the backward recursion gain and the calculated amount of the predicted valueare decreased, and the prediction accuracy is improved; as well as the anti-interference and stability of the system are effectively strengthened. The experimental result on Turtlebot mobile robot platform verifies the high effectiveness and stability of this algorithm in position and attitude estimation.
Extended Kalman filter Singular value decomposition Optimal smoothing algorithm Optimal estimation Position tracking
薛永胜(1989-),男,现为西南科技大学检测技术与自动化装置专业在读硕士研究生;主要研究方向为工业智能控制、智能检测技术与自动化装置。
TP202
A
10.16086/j.cnki.issn1000-0380.201504005
四川省科技厅科技支撑计划项目(编号:2014RZ0049);
2014四川省科技支撑计划项目(编号:2014GZ0021)。
修改稿收到日期:2014-10-19。
