捷联惯导系统极区导航算法优化设计及误差特性分析

张海峰，张礼伟，王兴岭，李 琳，仲 岩

（天津航海仪器研究所，天津 300131）

捷联惯导系统极区导航算法优化设计及误差特性分析

张海峰，张礼伟，王兴岭，李 琳，仲 岩

（天津航海仪器研究所，天津 300131）

采用格网坐标系下的力学编排方案能够有效解决常规惯导系统力学编排方案在极区航向误差急剧发散且无法实现定位定向的难题。格网坐标系力学编排方案可以直接获得格网航向，以及地心地固坐标系下的位置坐标，且输出航向精度及定位精度不随纬度的增高而变差。通过深入研究格网坐标系力学编排方案的误差传播规律，详细分析了高纬度下格网航向保持高精度输出的数学机理。针对格网坐标系力学编排方案在极点附近存在计算奇异值的问题，提出了一种通过格网坐标系和地球坐标系间的位置方向余弦矩阵更新解算替代由地心地固位置坐标求解经纬度三角函数值的优化算法，实现了真正意义上的格网坐标系力学编排方案在极区的“无死角”导航能力。仿真分析了载体沿经线穿越极点运动时的算法性能，并与固定指北力学编排方案进行了比较，结果表明，相比于传统导航方案，格网系下输出的航向误差不随纬度升高而发散，导航精度与低纬度区域导航能力相当。

极区导航；格网坐标系；误差特性；算法优化

随着航空、航海事业的蓬勃发展以及国际政治经济的不断变化，对海军作战舰艇的全球作战能力提出了更高的要求。由于极区地理经线快速收敛，导致传统地理导航坐标系失效。虽然自由和游移方位惯导可在极区完成姿态方向余弦矩阵和位置方向余弦矩阵的解算，但从矩阵中提取航向信息和经度信息时存在奇异值。采用格网线取代传统的地理经纬线对地表重新划分是解决该问题的有效手段之一。

以载体所在点处平行于格林尼治子午面的平面作为格网平面，以载体所在点的水平面作为切平面，格网平面与切平面的交线定义为格网北向，格网北向同真北方向的夹角为格网夹角σ，格网天向同地理天向重合，格网东向在切平面内与格网北向垂直构成右手直角坐标系，此即为格网坐标系,如图1所示。以平行于格林尼治子午线方向作为航向参考可避免纬度升高经线收敛造成的定向基准难题，因此，在格网系下编排惯导力学方程可以有效解决常规力学编排方案所面临的极区溢出问题。

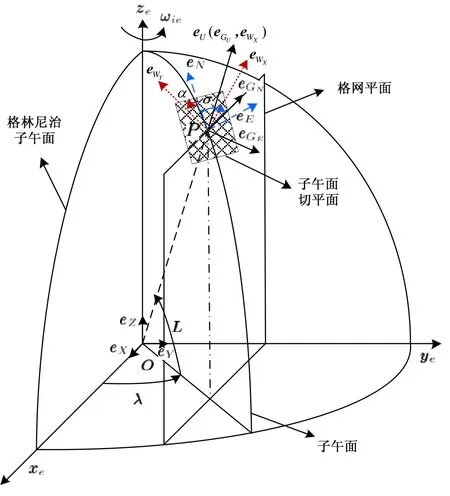
图1 格网坐标系及地心地固坐标系Fig.1 Grid navigation coordinate and ECEF coordinate

1 格网系力学编排方程

对于捷联惯导系统，格网导航力学编排的姿态方向余弦矩阵、速度和位置微分方程可表述如下：

式(2)～(5)中，σ为格网角，vGE和vGN为格网系内的东速和北速，RM和RN分别为子午圈和卯酉圈曲率半径。

从式(1)～(5)可知，微分方程中相关物理量的计算需要经纬度的三角函数值，该值可以由地心地固坐标系内的位置坐标（x, y, z）与经纬度（L, λ）的三角函数关系求得。但在无限靠近极点的过程中x, y→0，使得经度的三角函数值出现奇异值，导致导航解算出现错误。

2 格网系导航算法优化

根据方向余弦矩阵微分方程可知：

将式(13)代入式(11)，可得：

对式(3)微分，可得：

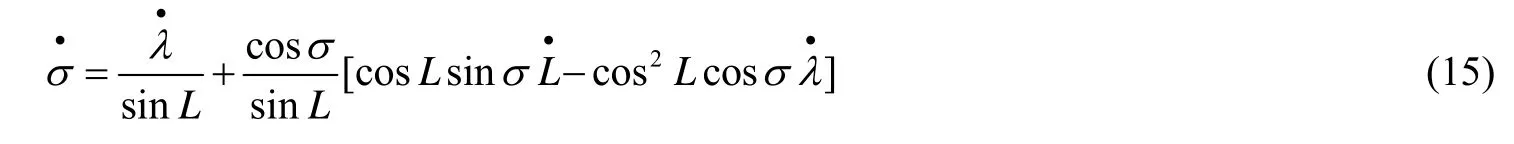
将式(15)代入式(8)，经过整理可得：

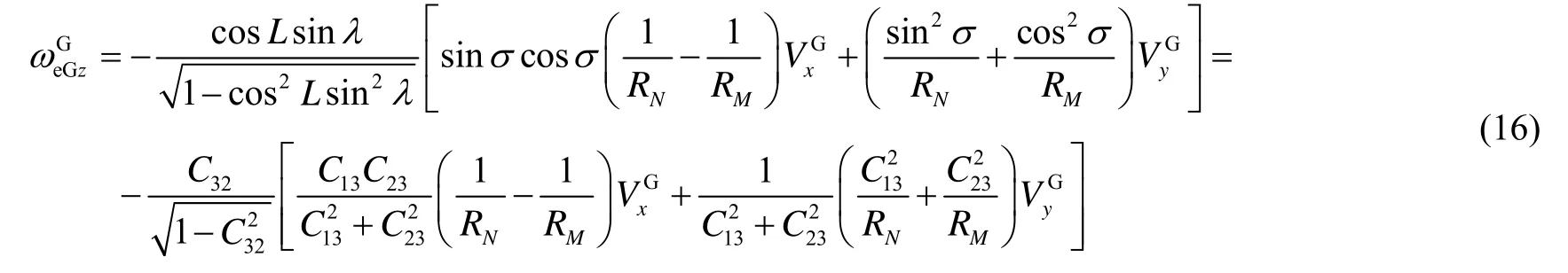
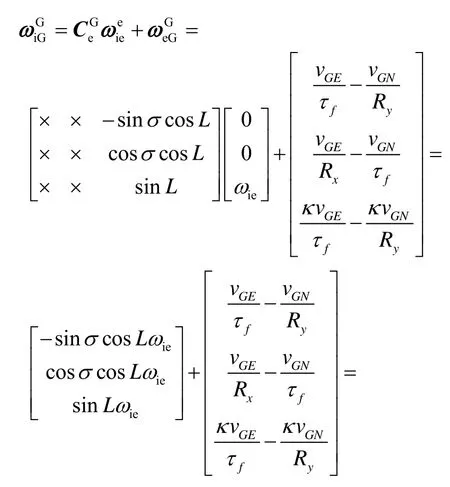
至此，综合式(14)和式(16)可得到 ωeGG的各分量表达式为

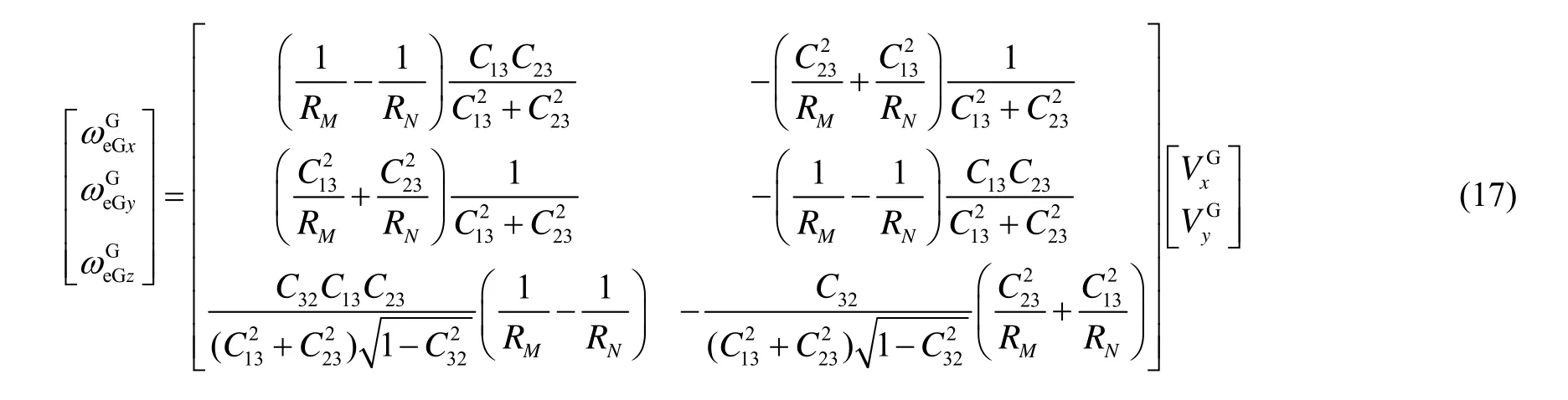
式(17)可以简化为

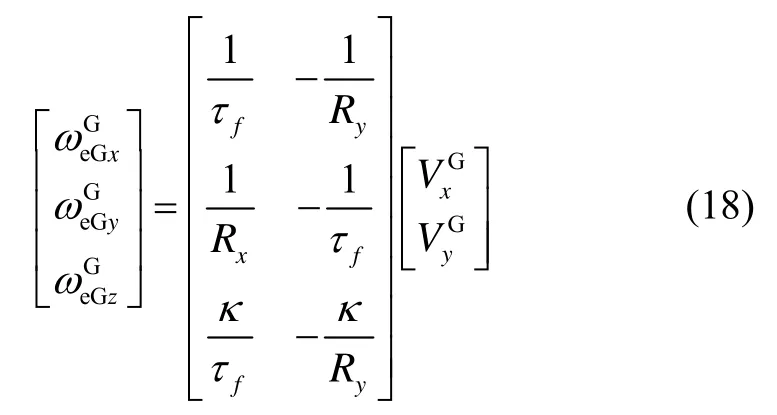
至此，综合式(1)(6)和(18)，可得极区导航算法的完备微分方程：

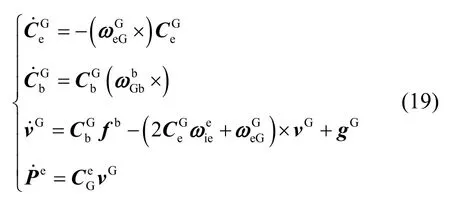
3 误差特性分析

格网系下平台误差角误差模型为

式中：

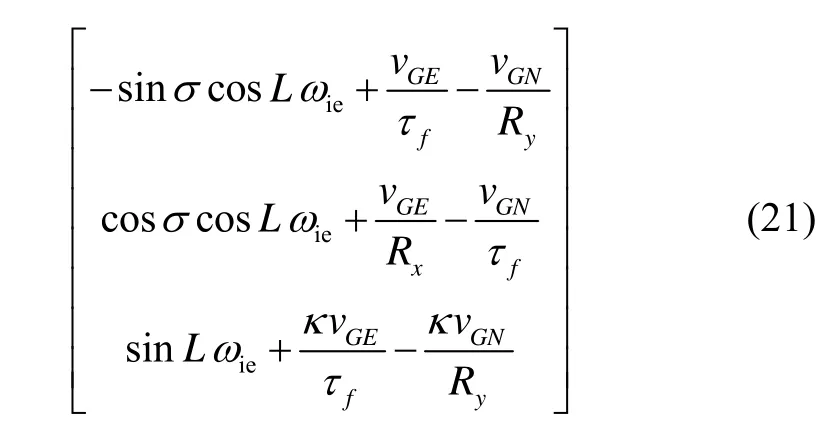
式中， Λ（˙）表示求导函数。由式(22)可以看出，格网系内的误差角中不含有随纬度升高计算溢出项tanL。因此，在高纬度地区进行格网系内导航解算，相比于地理系解算，可以获得更高的精度。经过推导可知，格网角σ满足如下关系式：

对式(23)求一阶导数：

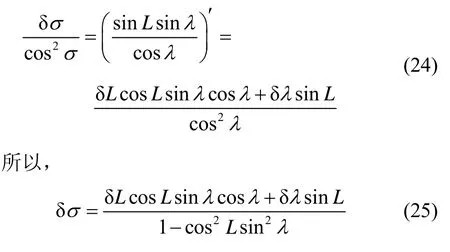
又因为

由式(26)可知，随着纬度的升高，经度误差迅速发散，因此，格网角误差δσ亦随之发散。

地理系航向误差为

因此可知，随着纬度升高，在地理系内航向误差会发散，而在格网系内航向误差不发散，发散项为格网角误差。这样，在格网系内求解航向，相当于将地理系内的航向误差发散分量剥离出去，因此可以得到更高的输出精度。

4 仿真结果及分析

为验证本文设计的极区导航算法的正确性，假设载体沿着某条经线向极点运动，并跨越极点。设初始位置为[85°N，0°E（W），0 m]，载体速度为20 kn，运动时间为24 h。惯性器件参数为：三个陀螺常值漂移0.002 (°)/h，三个加速度计零偏稳定性为50 μg。

图2～图5为本文优化的极区格网算法的姿态误差、速度误差与位置误差图。图6和图7为常规导航算法的姿态误差与位置误差图线。由图2～图5可以看出，优化的格网导航算法在跨越极点的过程中导航解算无奇异值，且24 h航向误差约为3′，定位精度约为1.2 n mile，导航精度与低纬度导航精度相当，完全能够满足使用需求。

根据格网系下力学编排误差方程可得航向误差受zε激励的时域解析式为

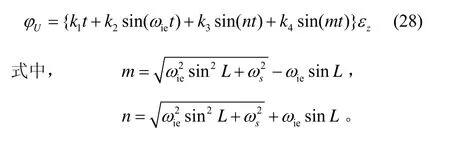
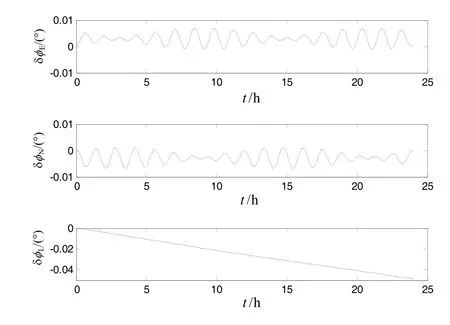
图2 极区格网优化算法的姿态误差Fig.2 Attitude error of grid optimization algorithm in polar region

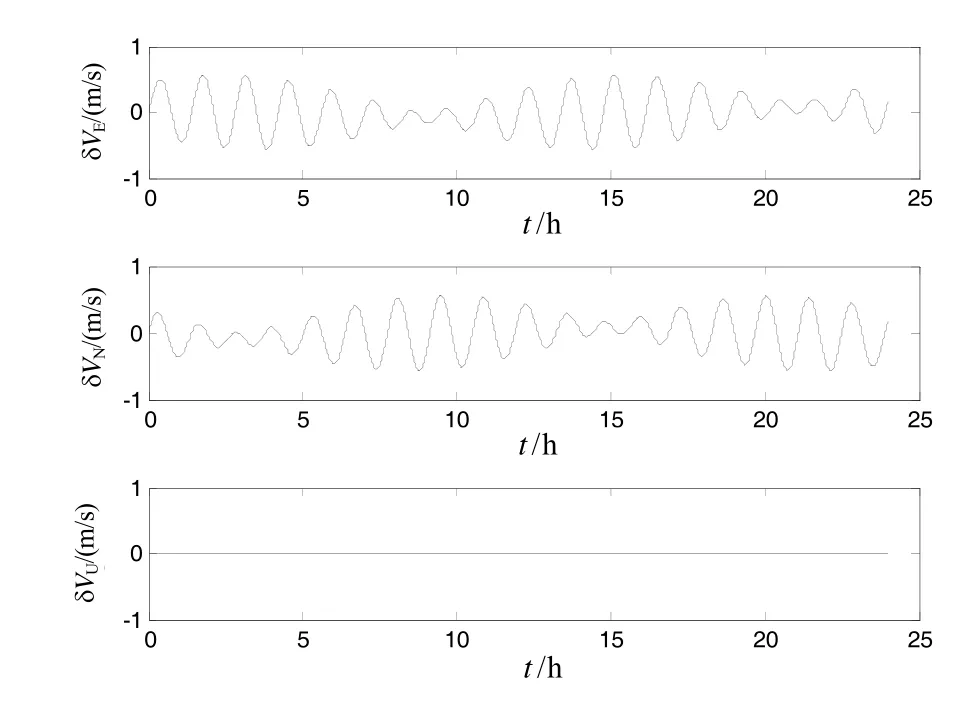
图3 极区格网优化算法的速度误差Fig.3 Velocity error of grid optimization algorithm in polar region

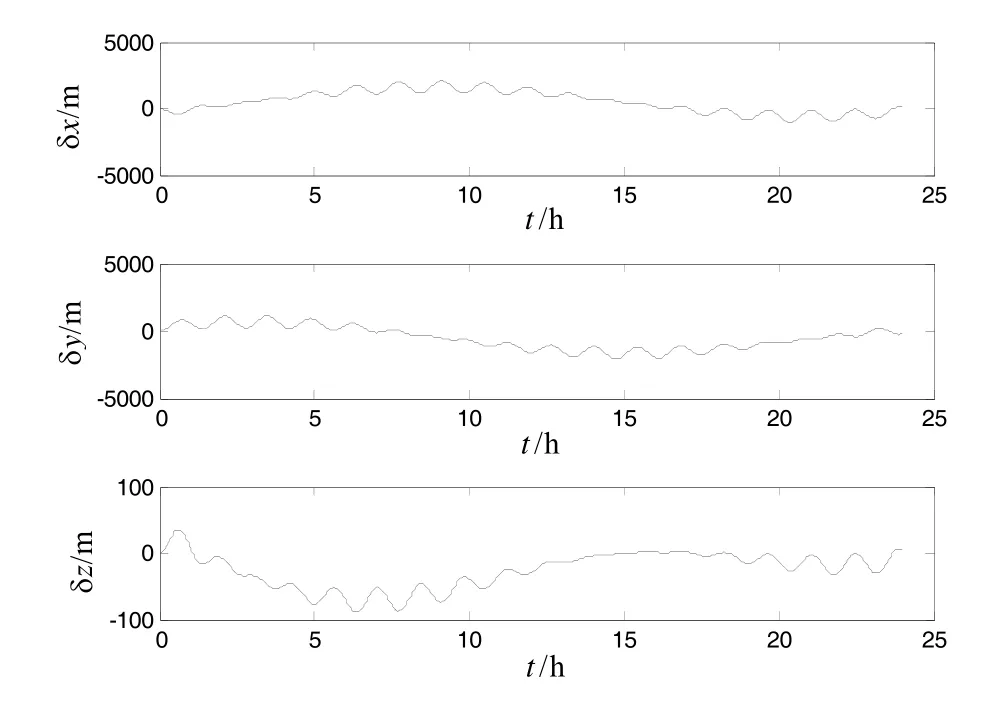
图4 极区格网优化算法的位置分量误差Fig.4 Position error of grid optimization algorithm in polar region

图5 极区格网优化算法的24 h定位误差Fig.5 24 h positioning error of grid optimization algorithm in polar region

图6 极区常规导航算法的姿态误差Fig.6 Attitude error of conventional navigation algorithm in polar region

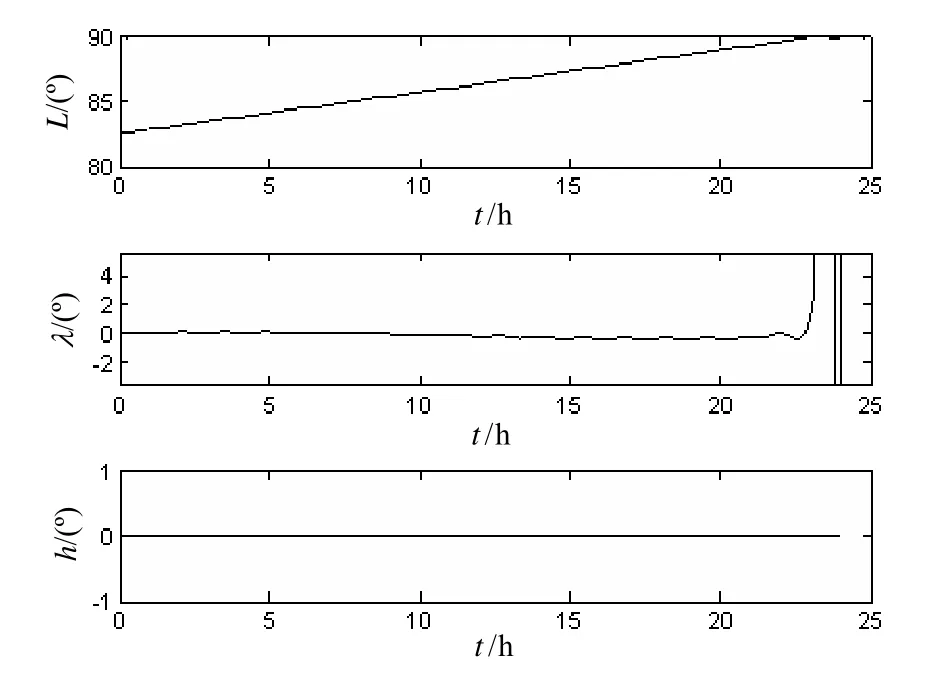
图7 极区常规导航算法的位置误差Fig.7 Position error of grid optimization algorithm in polar region

由式(28)可知，航向误差存在随时间发散项，经计算其系数值约为1.021左右，方位陀螺漂移为0.002 (°)/h的24 h航向误差为2.94′，与仿真结果相当。

由图6和图7可以看出，常规导航算法在纬度升高的过程中，航向误差与经度误差逐渐发散放大，当靠近极点的过程中出现奇异值。这是由于航向与经度解算过程中与tanL有关，当纬度升高时该正切值急剧增大，使得航向误差与经度误差被放大，使导航解算无法继续。

5 结 论

格网导航算法通过重新建立参考坐标系，克服了极区经线收敛引起的惯导系统定位定向难题。但在格网系下进行导航解算时，由地心地固位置坐标求取经纬度的三角函数值的过程中，当无限靠近极点时会出现奇异值，使得导航解算出现异常。

为解决此问题，设计了由格网坐标系与地球坐标系间的位置方向余弦矩阵更新迭代解算替代由ECEF位置求解经纬度三角函数值的优化算法，从而避免了在极点处出现解算奇异值的问题。从格网系下的航向误差方程出发，阐释了极区格网算法航向精度不随纬度升高而下降的数学机理。通过动态仿真试验表明，该算法在高纬度地区解算精度与低纬度地区相当，且解算过程稳定可靠，并无奇异，能够满足极区导航需求，具有重要的理论意义。

（References）：

[1] 周琪, 岳亚洲, 张晓冬, 等. 极区飞行间接格网惯性导航算法[J]. 中国惯性技术学报, 2014, 22(1): 18-22, 26. Zhou Qi, Yue Ya-zhou, Zhang Xiao-dong, et al. Indirect grid inertial navigation mechanization for transpolar aircraft[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 18-22, 26.

[2] 吴枫, 秦永元, 周琪. 机载武器极区传递对准算法[J].中国惯性技术学报, 2013, 21(2): 141-146. Wu Feng, Qin Yong-yuan, Zhou Qi. Airborne weapon transfer alignment algorithm in polar regions[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 141-146.

[3] Department of the Air Force. Air navigation (US.Air Force Pamphlet 110-216)[M]. Create Space Independent Publishing Platform, 2013.

[4] Savage P G. Strapdown analytics II[M]. Maple Plain, Minnesota: Strapdown Associates, 2009.

[5] 李倩, 孙枫, 奔粤阳, 等. 基于横坐标系的捷联惯导系统极区导航方法[J]. 中国惯性技术学报, 2014, 22(3): 288-295. Li Qian, Sun Feng, Ben Yue-yang, et al. Polar navigation of strapdown inertial navigation system based on transversal frame in polar region[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 288-295.

[6] 姚逸卿, 徐晓苏, 童金武. 极区间接横向惯性导航方法[J]. 中国惯性技术学报, 2015, 23(1): 29-34. Yao Yi-qing, Xu Xiao-su, Tong Jin-wu. Indirect transverse inertial navigation algorithm in polar region[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 29-34.

[7] Wang Xian-wei, Cheng Xiao, Hui Feng-ming, et al. Navigation in fast ice near the Zhongshan Station, Antarctica[J]. Marine Technology Society Journal, 2013, 48(1): 84-91.

[8] Gao Xing-xin, Heng Liang, Walter T, et al. Breaking the ice: Navigating in the arctic[C]//Proc. of the 24thInternational Technical Meeting of The Satellite Division of the Institute of Navigation. Portland, OR, 2011: 3767-3772.

[9] Andriani S, Lysandros T. Choosing a suitable projection for navigation in the arctic[J]. Marine Geodesy, 2013, 36(2): 234-259.

[10] Andreev A G, Ermakov V V, Mafter M B. High latitude trials of modern Russian marine compasses[C]//Position Location and Navigation Symposium. 2006: 636-644.

Optimization design and error analysis of strapdown inertial navigation system mechanization in polar region

ZHANG Hai-feng, ZHANG Li-wei, WANG Xing-ling, LI Lin, ZHONG Yan
(Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

Grid inertial navigation mechanization could effectively solve the problems of heading and positioning errors’ increase in high latitudes. They could directly get the grid heading as well as the position in the earth-centered earth-fixed coordinates (ECEF) without degrading the accuracy with the increasing of latitude. Based on the analysis on the error model of the grid navigation mechanization, the mathematical mechanism why grid heading keeps high-accuracy output at high latitude is analyzed. In view that navigation calculation had singular value at the polar point, an optimized mechanization is presented, which uses position direction cosine matrix (DCM) updating instead of the ECEF to calculate the trigonometric function value of latitude and longitude. Simulation analyzes the performance when the carrier crosses the polar along the longitude line, and the results show that, compared with the traditional navigation mechanization, the heading error in the grid frame doesn’t diverge when the latitude increases, and the navigation accuracy is equivalent to that of low-latitude navigation.

polar navigation; grid frame; error characteristics; mechanization optimization

U666.1

：A

2015-09-15；

：2015-11-27

装备预研基金重点项目（9140A09031514CB37031）

张海峰（1986—），男，工程师，从事惯性导航技术研究。E-mail: tjuzhanghaifeng@126.com

1005-6734(2015)06-0701-06

10.13695/j.cnki.12-1222/o3.2015.06.001