平台式重力仪测量数据的卡尔曼滤波处理

蔡体菁，周 薇，鞠玲玲

（东南大学 仪器科学与工程学院，南京 210096）

平台式重力仪测量数据的卡尔曼滤波处理

蔡体菁，周 薇，鞠玲玲

（东南大学 仪器科学与工程学院，南京 210096）

根据三轴惯性平台海空重力仪的特点，在重力测量数据处理中，把重力异常作为状态量，建立了扩展卡尔曼滤波状态方程和观测方程，并阐述了三轴惯性平台海空重力仪重力测量数据处理步骤。依据给出的卡尔曼滤波方程，应用平滑卡尔曼滤波方法，对三轴惯性平台海空重力仪的海洋重力测量数据进行了处理。海空重力仪测量结果为：南北重复测线内符合精度为0.2 mGal，东西重复测线内符合精度为0.4 mGal，空间分辨率为650 m。

海空重力仪；数据处理；卡尔曼滤波；重力异常

自20世纪90年代以来，海空重力仪发展迅速，出现了一系列商用二轴和三轴稳定平台式海空重力仪[1-2]。二轴稳定平台式海空重力仪有：美国Micro-g LaCoste公司的L&RS、SII海空重力仪、TAGS航空重力仪，俄罗斯中央电气仪表所的CHEKAN-AM海空重力仪。三轴稳定平台式海空重力仪有：加拿大Sander地球物理公司的AIRGrave航空重力仪，俄罗斯重力技术公司的GT-A航空重力仪、GT-M海洋重力仪。近十几年来，我国海空重力仪发展也很迅猛[3-4]。中国船舶重工集团公司天津航海仪器研究所和中国科学院测量与地球物理研究所都分别研制出二轴稳定平台式重力仪，北京自动化设备研究所研制出三轴惯性平台海空重力仪。

目前国际上大多数稳定平台式海空重力仪配套的处理软件都是应用IIR滤波器和FIR滤波器来处理重力数据[5]，而GT-1A航空重力仪配套的重力处理软件不仅用了FIR低通滤波，而且还用了卡尔曼滤波技术[6-7]。国内学者提出用小波方法处理航空重力测量数据。东南大学在研究航空重力数据处理的FIR滤波、IIR滤波和小波等方法[8]的基础上，提出用平滑卡尔曼滤波方法处理重力数据。本文针对国产三轴惯性平台海空重力仪，给出重力测量数据的平滑卡尔曼滤波方法，以及处理重力测量数据的结果。

1 三轴惯性平台海空重力仪

国产三轴惯性平台海空重力仪是由三轴惯性平台、重力敏感器、二次电源、控制电路、GPS接收机、计算机和显控存储装置等组成的。三轴惯性平台使用的惯性敏感器是2个两自由度动力调谐陀螺和3个石英挠性加速度计；重力敏感器采用小量程高精度的石英挠性加速度计；计算机进行导航计算；显控存储装置用来控制海空重力仪完成各个工作流程，存储和显示海空重力仪测量数据、导航参数和状态。

海空重力仪工作流程包含准备和测量二个阶段，其流程见图1所示。

图1 海空重力仪工作流程图Fig.1 Working flowchart of the sea/air gravimeter

准备阶段主要是使惯性器件精度达到要求，完成重力仪的初始对准。具体完成的任务有：① 通电预热：重力仪内部所有分部件均启动工作，并对稳定平台进行温度控制；② 参数自标定：利用稳定平台框架实现惯性器件的不同空间标定位置，标定出陀螺、加速度计的关键参数；③ 抗扰动对准：调整稳定平台坐标系精确进入测量工作状态。

测量阶段包括三个步骤：① 前校测量：完成准备后，在载体不移动的情况下，进行一段时间的静态测试，自动记录重力仪和卫星数据；② 重力测量：平台系统工作于动态导航状态，自动记录重力仪和卫星的数据，是重力测量的主体工作；③ 后校测量：在完成测量后，载体回到出发点，重新进行一段时间的静态测试，自动记录重力仪和卫星数据。最后将所有数据存贮到硬盘设备中保留。

2 平滑卡尔曼滤波

国产三轴惯性平台海空重力仪的重力传感器是被垂直安装在一个带舒拉调谐的三轴稳定平台上的。在航行中，校正回路可以将GPS的位置和速度信息提供给平台作阻尼，平台导航坐标系为游动方位坐标系。它提供的信息为：三个加速度计的输出，载体的姿态、温度、平台参数，GPS移动站的星历、伪距、多普勒频移、载波相位等原始数据。利用以上信息以及GPS基站的原始信息，能够计算得到测线上的自由空间重力异常。自由空间重力异常Δg可以通过对惯性导航比力方程的变形得到，其方程为

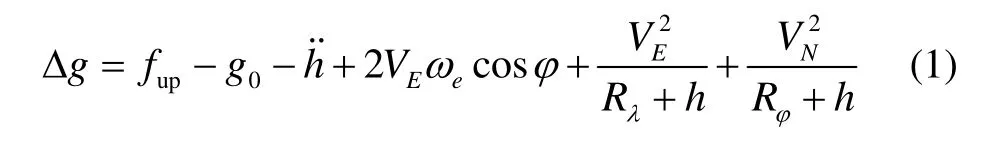
式中：fup为加速度计的垂向分量，g0为正常重力场，为载体的垂向加速度，ωe为地球旋转角速度，VE和VN为载体的东向和北向速度，φ为载体的纬度，Rλ和 Rφ分别为参考椭球子卯酉圈和午圈曲率半径。

在工作时，海空重力仪的三轴惯性平台作舒拉或阻尼振荡，会引起平台倾斜，即平台存在一个失准角，方程(1)可改写为

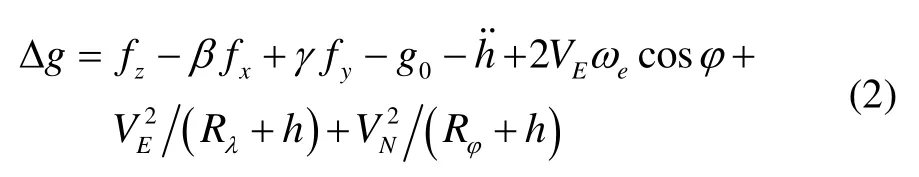
式中： fz是重力传感器输出， fx、 fy是水平加速度计输出，β、γ是平台失准角。

在地球物理学中，重力异常可以用随机统计模型来描述。本文采用如下近似模型来描述重力异常：

式中：ρ为噪声强度，q为白噪声。

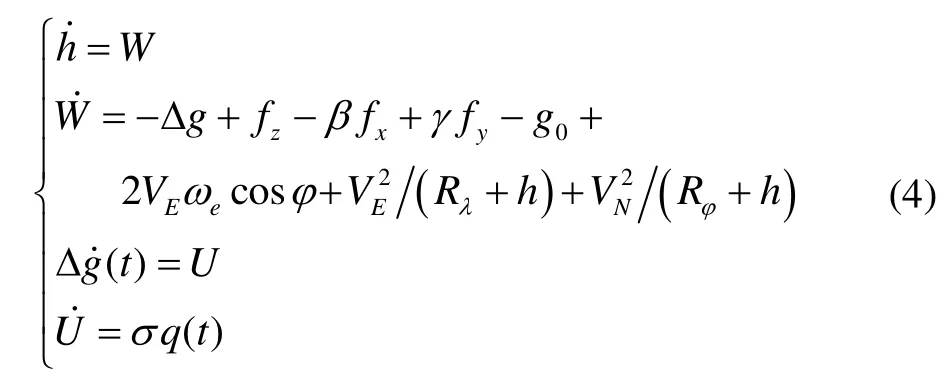
状态向量为 X=[h, W ,Δ g, U]T。

用差分 GPS的高度信息作为卡尔曼滤波的观测信息，观测方程为

式中：h为高度，H为测量矩阵，ν为测量噪声。式(4)和式(5)可以写成随机线性离散系统形式：

式中：Xi是 ti时刻的状态向量；Φi+1,i是 ti时刻到 ti+1时刻的状态转移矩阵；Bi是系统输入矩阵；ui是系统输入向量；Gi是系统噪声输入矩阵；wi是系统噪声向量；Zi是ti时刻的观测向量；Hi是观测矩阵；vi是观测噪声向量；wi和vi均是零均值高斯白噪声且相互独立，其噪声强度分别为Qi和Ri。

应用平滑卡尔曼滤波方法求解重力异常。方程(6)的卡尔曼滤波为

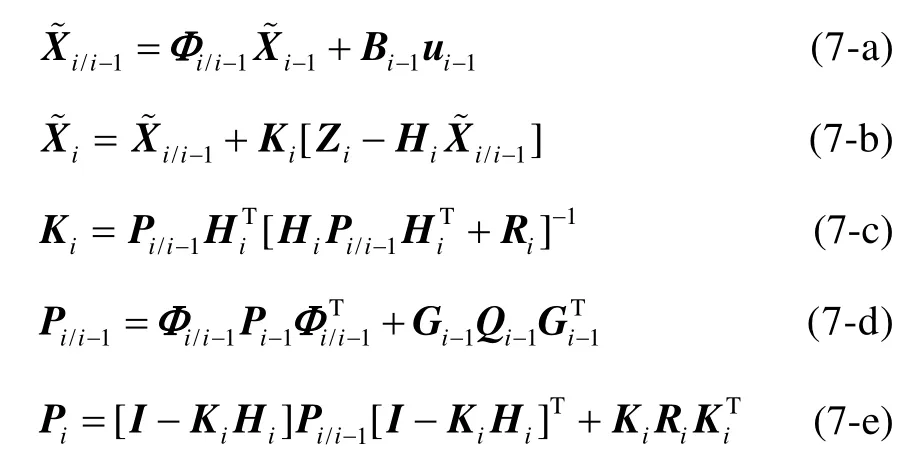
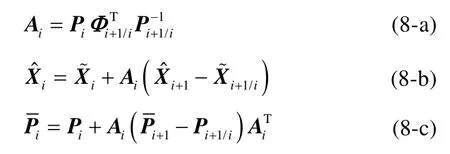
3 试验数据处理结果

2015年6月国产三轴惯性平台海空重力仪在青岛进行了近海重力测量试验。海空重力仪放在近海科考01号船上，GPS基站设在码头岸上，船以13 n mile/h的平均速度在近海上航行，沿南北和东西两条航线做重复线测量。试验结束后，对GPS基站数据和海空重力仪测量数据进行事后重力数据处理。

三轴惯性平台海空重力仪重力测量数据后处理步骤如下：首先利用GPS基站和GPS移动站的原始数据，进行差分GPS的伪距、多普勒频移和载波相位计算方法，得到船航行的位置和速度；其次根据GPS提供的位置、速度信息和三轴惯性平台海空重力仪的输出信息，用卡尔曼滤波技术估计出惯性稳定平台失准角、重力传感器误差和加速度计误差；然后对各种误差进行修正，再利用上面给出的平滑卡尔曼滤波，计算出测线上的自由空间重力异常。图2给出了三轴惯性平台海空重力仪重力数据处理流程。

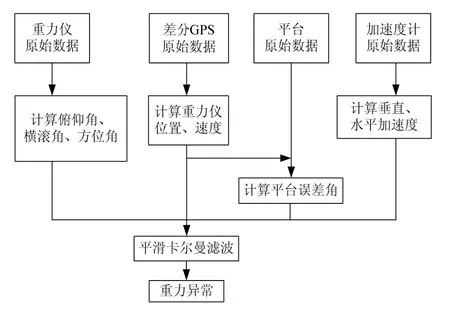
图2 重力数据处理流程Fig.2 Flowchart of gravity data processing

根据上述三轴惯性平台海空重力仪重力测量数据处理步骤，对近海重力测量试验数据进行处理，其结果是：南北重复测线内符合精度为0.2 mGal，东西重复测线内符合精度为0.4 mGal，空间分别率为650 m，自由空间重力异常曲线如图3和图4所示。

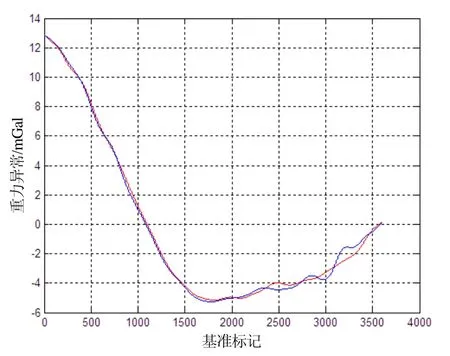
图3 南北重复线重力异常值Fig.3 Gravity anomaly of north-south repeated lines

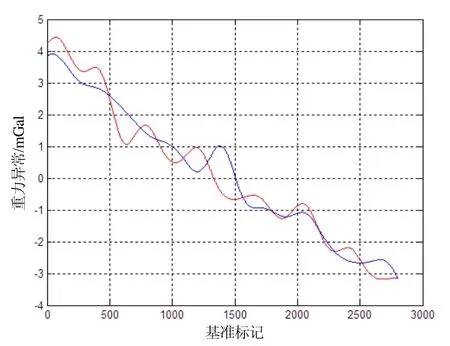
图4 东西重复线重力异常值Fig.4 Gravity anomaly of east-west repeated lines

4 结 论

国产三轴惯性平台海空重力仪的近海重力测量试验结果表明，该海空重力仪具有良好的动态测量性能，测量精度优于0.5 mGal。本文给出的卡尔曼滤波状态方程以及平滑卡尔曼滤波方法能够很好地处理三轴惯性平台海空重力仪重力测量数据。对于目前处理海空重力仪重力测量数据唱主角的FIR和IIR低通滤波器方法来讲，卡尔曼滤波将是一个不错的选择方法。

（References）：

[1] Brochure—TAGS air III gravity meter[EB/OL]. [2015-08-09]. http://www.microglacoste.com.

[2] Sokolov A V. High accuracy airborne gravity measurements methods and equipment[C]//18th IFAC World Congress. Milano, 2011: 1889-1891.

[3] 奚碚华, 于浩, 周贤高. 海洋重力测量误差补偿技术[J]. 中国惯性技术学报, 2011, 19(1): 1-5. Xi Bei-hua, Yu Hao, Zhou Xian-gao. Compensation of ocean gravity measurement errors[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 1-5.

[4] 胡平华, 黄鹤, 赵明, 等. 轻小型高精度惯性稳定平台式航空/海洋重力仪研究[C]//中国惯性技术学会第七届学术年会论文集. 2015: 30-35. Hu Ping-hua, Huang He, Zhao Ming, et al. Study of airborne/marine gravimeter based on high precision inertial stabilized platform. 2015: 30-35.

[5] Ayres-Sampaio D, Deurloo R, Bos M, et al. A comparison between three IMUs for strapdown airborne gravimetry [J]. Surveys in Geophysics, 2015: 1-16.

[6] Bolotin Y V, Vyazmin V S. Gravity anomaly estimation by airborne gravimetry data using LSE and minimax optimization and spherical wavelet expansion[J]. Gyroscopy and Navigation, 2015, 6(4): 310-317.

[7] Smoller Y L, Yurist S S, Golovan A A, et al. Using a multiantenna GPS receiver in the airborne gravimeter GT-2a for surveys in polar areas[J]. Gyroscopy and Navigation, 2015, 6(4): 299-304.

[8] Zhou Wei, Cai Ti-jing. Study on filtering methods of airborne gravity[C]//Applied mechanics and materials, 2013, 333-335: 516-521.

[9] Peter S M. Stochastic models, estimation and control[M]. New York: Academic Press, 1982.

Processing for measurement data of platform gravimeter by Kalman filter

CAI Ti-jing, ZHOU Wei, JU Ling-ling
(School of instrument science and engineering, Southeast University, Nanjing 210096, China)

Based on the characteristics of three-axis inertial platform sea/air gravimeter, the state and measurement equations of the extended Kalman filter are given, which take the gravity anomaly as a state vector. Data processing procedure of the three-axis inertial platform sea/air gravimetry data is presented by using the equations and the smooth method of Kalman filter. The measurement results on the sea/air gravimeter show that the internal accordance accuracies of north-south and east-west repeated lines are 0.2 mGal and 0.4 mGal, respectively, and the spatial resolution is 650 m.

sea/air gravimeter; data processing; Kalman filter; gravity anomaly

P631.1

：A

2015-09-21；

：2015-11-28

国家国际科技合作专项项目（2014DFR80750）；国家863计划（2011AA060501）

蔡体菁（1961—），男，教授，博士生导师。Email: caitij@seu.edu.cn

1005-6734(2015)06-0718-03

10.13695/j.cnki.12-1222/o3.2015.06.004