基于提前/拖期的随机期望值模型及序优化算法
2015-06-14赵志纲孙征虎
□ 赵志纲 □ 孙征虎
中国空间技术研究院 北京 100094
工序加工时间的不确定直接影响着原材料、工装夹具、设备人员等一系列生产准备工作的开展,严重制约着车间零部件生产的稳定性和有序性。相对于确定性调度问题,在加工时间不确定的作业车间调度问题中,工序加工时间为不确定随机变量,从而导致其目标量也为变量。由于各工序的开、完工时间无法准确获得,使该类问题的调度解只能表示为机器上的加工序列。另外,随机变量的引入,导致问题空间更为庞大,计算效率更加低下。因此,加工时间不确定的作业车间调度问题具有参数不确定性、目标变量化、调度解序列化、问题空间庞大、求解效率低下的特点。
程蓉[1]研究了随机机器故障干扰的作业车间鲁棒调度问题,提出了一种基于邻域的鲁棒性指标,指出将该鲁棒性指标结合优秀的重调度方法是提高调度鲁棒性的有效措施,但在机器故障比较严重时稍有不足。朱海平等[2]提出了一种支持多目标和多优先级车间调度策略的随机规划模型,并给出了求解算法。刘琳等[3]针对在加工时间大范围不确定性的调度环境中,单机Just-in-time调度,设计出一种两层协同进化遗传算法,解决了绝对鲁棒调度优化问题,使加工时间变化范围内预调度的最差性能最优化。Beck等[4]提出了加工时间不确定条件下的Job Shop调度问题的相关理论,并给出了证明过程,仿真结果表明了这些理论的可行性和有效性。Selcuk Goren等[5]研究了不确定因素干扰下的单机调度问题,提出了鲁棒性和稳定性两种指标,并设计了代理指标,在考虑工作时间和修复时间服从概率分布的情形下,采用禁忌搜索算法进行优化求解,仿真结果表明,其中一种代理指标的结果优于当时已有的最优结果。于艾清等[6]针对并行机调度中的不确定工件加工时间,提出用粗糙变量来表示不确定量,并建立粗糙期望值规划模型,设计了进化规划算法,并改进了编码方式和变异方法。周强等[7]讨论了在不确定加工时间和机器故障的情况下,多目标流水车间调度问题的优化过程,基于最大流程时间和最大延迟时间两类目标,提出一种多目标遗传算法,实验结果表明该算法能较好地解决不确定条件下的Flow Shop调度问题。陈宇等[8]针对不确定环境下的Job Shop调度,提出了一种基于设备整体效能的具有鲁棒性的预测调度实现方法,并设计了一种基于多Agent协作机制的预测调度系统模型。
本文基于提前/拖期这类非正规性能指标无法应用双空间协同前摄调度方法的特点,引入了与调度解序列吻合度较高的序优化思想。该算法将进化策略嵌入到序优化过程中,从粗糙的评价模型到精确的评价模型,分阶段进行优化,先采用进化算法进行粗糙优化,而后以精确模型评价各阶段的较好解,达到从粗到精、逐步优化的目的。最后通过算例仿真,验证了该算法的正确性和有效性。
1 随机期望值模型
提前/拖期是为了适应及时生产模式而提出的,它从控制生产成本的角度出发,对每个工件设置交货期,工件提前完工产生提前惩罚成本,拖期完工产生拖期惩罚成本,从而尽可能地促使每个工件在交货期节点准时完工。提前/拖期指标是指所有工件的提前/拖期惩罚成本之和,是一种非正规性能指标。
基于提前/拖期指标的加工时间不确定的作业车间调度问题可描述为:n 个工件 J={J1,J2,...,Jn}在 m 台机器 M={M1,M2,...,Mm}上加工,每个工件 Ji有一组工序 O={,...,,且各工序的加工时间是一个不确定的随机变量(期望和标准差已知),其中,工件早于交货期完工将产生库存成本,工件晚于交货期完工则产生拖期惩罚成本。调度任务是在满足工艺路线、机器能力等约束的前提下,确定每台机器上的最佳加工顺序,使提前/拖期总惩罚成本最低。该随机期望值模型所需的数学符号见表1。
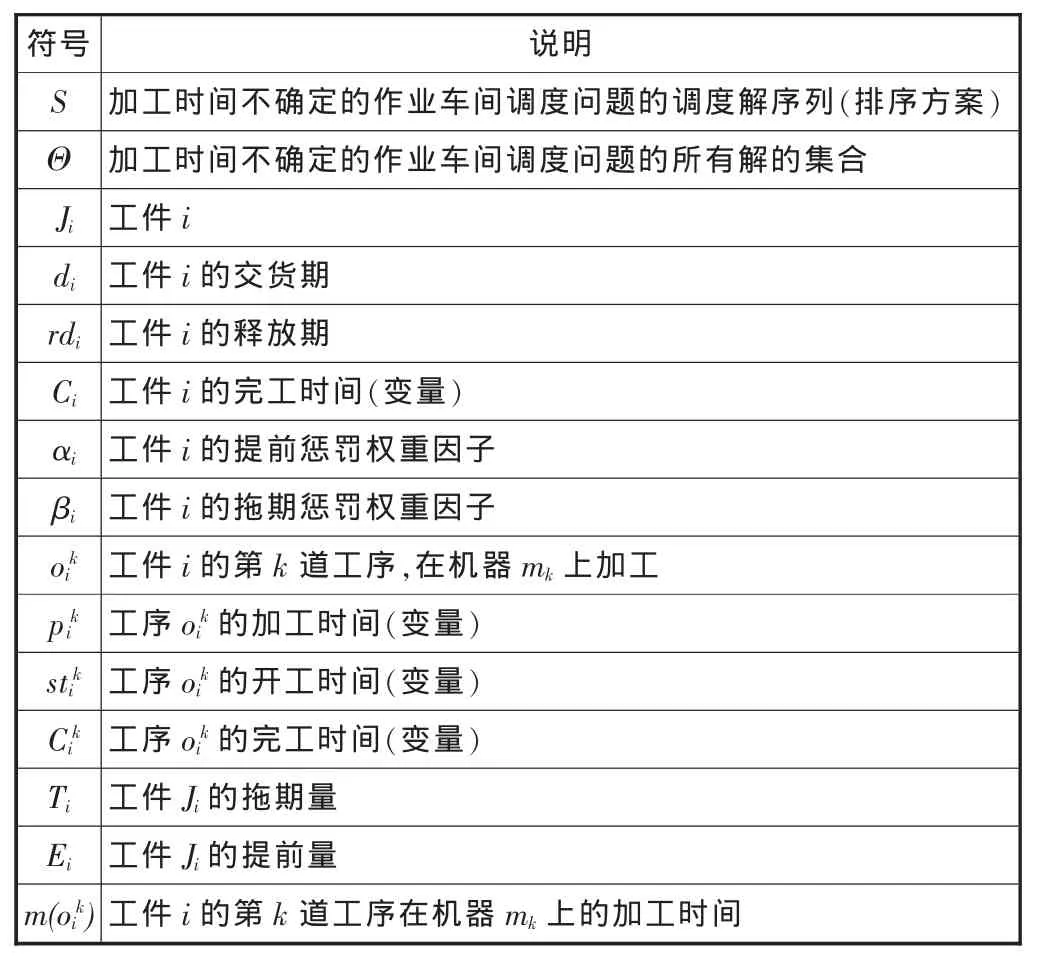
表1 随机期望值模型变量说明
基于提前/拖期指标的加工时间不确定的作业车间调度问题随机期望值模型如下:
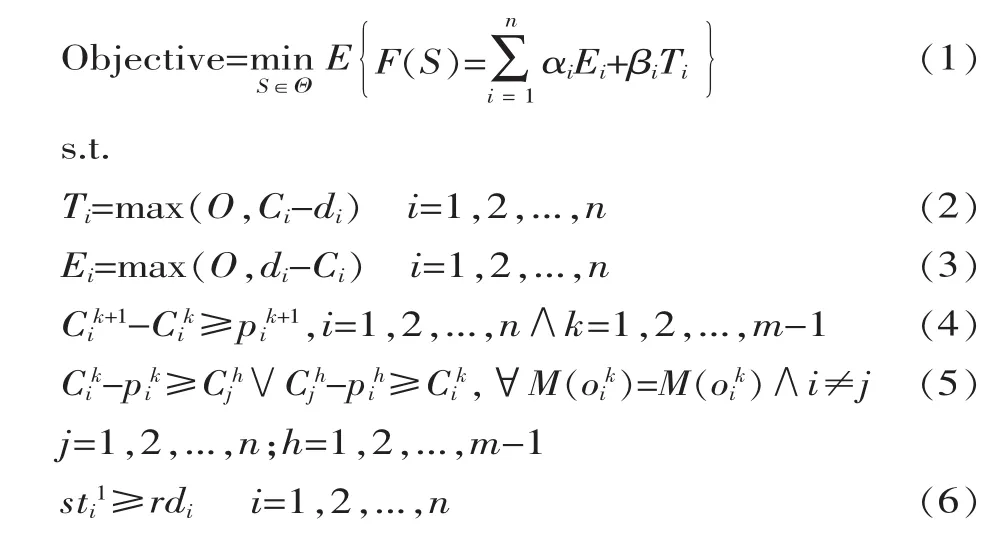
式(1)为目标函数,即总提前/拖期惩罚成本最小。由于工序加工时间是随机变量,使优化目标也成为变量,因此,对基于提前/拖期指标的加工时间不确定的作业车间调度问题随机期望值模型,其指标为总提前/拖期成本的期望值最小;式(2)为工件Ji的拖期量;式(3)为零件 Ji的提前量;式(4)为工艺顺序约束,即:同一工件Ji内不同工序之间的时序关系约束;式(5)为机器能力约束,即:Ji同一承制机床上加工工序队列的时序关系约束;式(6)为工件释放期约束,即:Ji的首道工序的开工时间不早于其释放期rdi。
为了获取式(1)的最优解,最易想到的方法就是遍历解空间Θ,目标函数值最小的解即为最优解。但是,随着解空间Θ的不断增大,这种枚举方法的计算量将呈指数级增长,在实际操作中是不可行的。
因此,基于仿真能够有效地描述系统的随机性特点,利用仿真的思想来对目标值进行评价,但由于式(1)中 F(S)是随机变量,其期望值要通过大量的仿真才可能近似获得,这将导致问题求解过程耗时过长。因此采用仿真评价函数代替目标函数(见式7),根据仿真次数建立评价模型,这样,一方面可以通过仿真次数控制目标值的稳定程度,另一方面大大减少了所需的仿真次数,得到了进化策略中进行解的评估的评价模型:
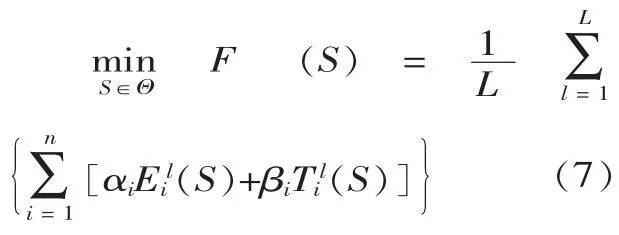
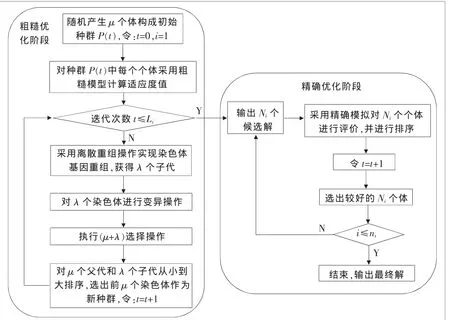
▲图1 序优化算法流程图
足够大的L能确保目标值的样本均值足够稳定。
2 序优化算法
由于加工时间不确定的作业车间调度问题的解为调度列,而序优化则采用序比较代替值进行比较,因此,将序优化方法引入到加工时间不确定的作业车间调度问题随机期望值模型中是非常吻合的。针对加工时间不确定的作业车间调度问题随机期望值模型,依据序优化和目标优化两个思想,在序优化中嵌入(μ+λ)进化算法,设计出序优化算法。
首先采用(μ+λ)进化算法对粗糙模型进行优化,得到性能较好的前N个解;然后在精确优化阶段增加仿真次数,提高精度,同时选取优良解的个数减少。通过逐步优化过程,最终获得能够满足需求的较好解。
因此,序优化算法首先需要确定分几个阶段优化、每个优化阶段有多少次仿真以及选出多少优良解这几个问题,其参数计算如下:
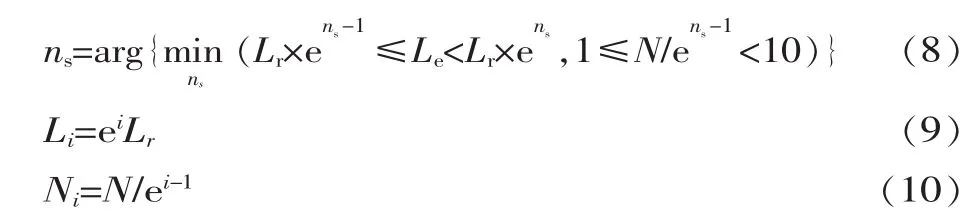
式中:ns为序优化算法优化过程的子阶段个数;Li为子阶段i仿真的次数;Ni为在子阶段i选择出的足够好解集的大小;le和lr为模型仿真的长度,且Le=105,Lr=368。
式(8)~式(10)分别给出了 ns、Li、Ni的计算方法,在Li和Ni的计算过程中,对非整数的Li和Ni需要进行圆整计算。其中式(8)既保证了ns是仿真长度大于精确模型需仿真长度的Le最小值,同时又保证了ns是最后子阶段足够好候选解集个数的最小值。序优化算法的流程图如图1所示。
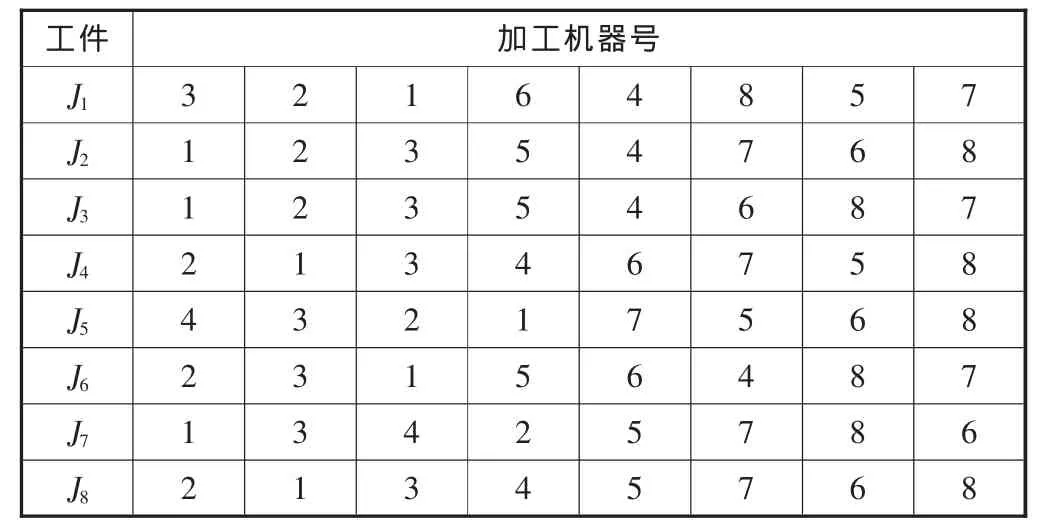
表2 8×8算例的工艺路线参数
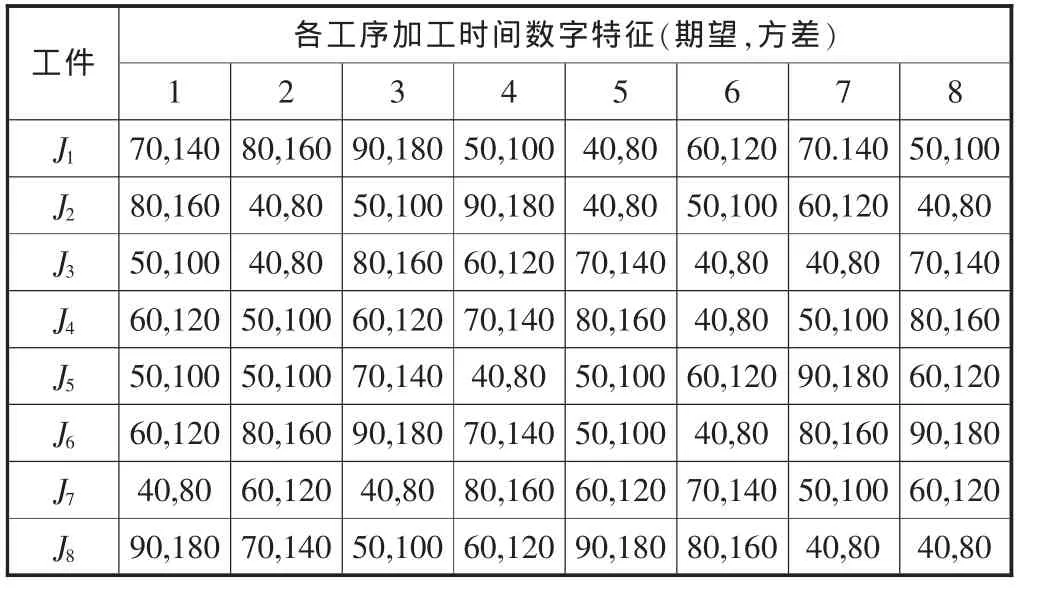
表3 8×8算例的各工序加工时间数字特征参数
3 算例分析
该测试算例设计过程为:8×8算例工艺路线参数见表2,不确定工序加工时间的数字特征 (期望和方差)见表3,交货期参数见表4,并且设计各工件的提前惩罚因子和拖期惩罚因子都是1。

表4 8×8算例的交货期参数
对于分阶段优化的序优化算法而言,首先需要确定有多少个子阶段、各阶段的仿真次数及候选解的规模。设定,依据式(8)计算出优化阶段个数ns=6,由式(9)、式(10)求出各阶段需仿真次数Li和候选解的规模 Ni,结果见表 5。

表5 序优化算法结果
4 结论
提出了基于提前/拖期指标的加工时间不确定的作业车间调度问题随机期望值模型,仿真结果表明,加工时间随机变量服从正态分布时的最优解序列,优于加工时间随机变量服从均匀分布时的最优解序列。
[1]程蓉.复杂生产环境下优化调度方法研究与系统实现[D].武汉:华中科技大学,2006.
[2]朱海平,邵新宇,张国军.不确定信息条件下的车间调度策略研究[J].计算机集成制造系统,2006,12(10):1637-1642.
[3]刘琳,谷寒雨,席裕庚.加工时间不确定的Just-in-time单机鲁棒调度[J].控制与决策,2007,22(10):1151-1154.
[4]Beck J Christopher,Wilson Nic.Proactive Algorithms for Job Shop Scheduling with Probabilistic Durations [J].Journal of Artificial Intelligence Research,2007,28:183-232.
[5]Selcuk Goren,Ihsan Sabuncuoglu.Robustness and Stability Measures for Scheduling:Single-machine Environment[J].IIE Transactions,2008,40(2):66-83.
[6]于艾清,顾幸生.基于粗糙规划的不确定加工时间的并行机调度[J].控制与决策,2008,23(12):1427-1431.
[7]周强,崔逊学.一种不确定条件下的多目标流水车间调度优化算法 [J].模式识别与人工智能,2009,22 (1):101-107.
[8]陈宇,陈新,陈新度.不确定环境下的多Agent鲁棒性预测调度研究[J].中国机械工程,2009(16):1937-1943.
