基于偶应力理论的层状岩体无网格数值模拟

孙玉周，陈根生

（中原工学院，郑州 450007）

近年来，层状岩体的薄层被发现具有弯曲效应，偶应力理论被很多学者应用到岩体的理论分析和数值模拟中。偶应力理论也被称作Cosserat连续介质理论，佘成学等建立了平面问题的Cosserat连续介质模型，研究了反倾向层状岩体弯曲变形破坏特性［1－2］；Ahikary等针对岩石层与节理分别采用不同的弹塑性参数，应用偶应力理论建立整体的力学模型［3－4］；刘俊等将层状岩体平面偶应力模型推广到空间范围［5－6］；李银平等建立了层状岩体的Cosserat扩展介质本构模型，证明了偶应力的引入能够合理地反映层状岩体的弯曲变形，对节理层面较多、层间距较小的情况尤其有效［7－8］；杨乐等应用偶应力理论结合有限元法对层状岩体地下洞室进行了数值模拟［9］。

偶应力理论考虑局部弯曲效应，曲率和应变是同等重要的基本变量，曲率可被近似为位移的二阶导数，在数值模拟时要求构造具有高阶连续特征的形函数，这给有限元法等传统的数值计算方法带来很大的麻烦［10］。无网格法是一种新型的数值计算方法，可以方便地构造高阶连续形函数，特别适用于高阶连续体的数值模拟［11－12］。本文利用无网格法的这一优点，建立层状岩体的无网格计算框架，对地下洞室进行数值模拟，研究基于偶应力的无网格法在层状岩体数值模拟中的应用效果。

1 偶应力理论

传统的偶应力理论在经典弹性理论的基础上考虑曲率κ1和κ2以及偶应力m1和m2的影响，在图1所示的单元体上，假定应力沿高度线性分布，偶应力是由线性应力梯度产生的单元面力偶。广义应力和广义应变分别定义如下［6，9］：

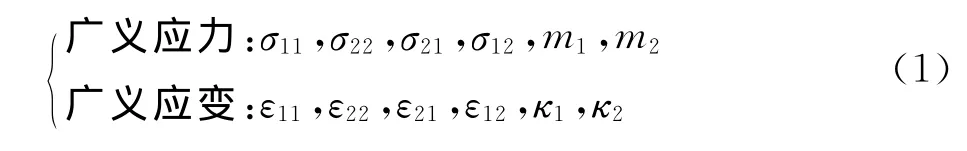
图1 单元体上的应力与偶应力以及偶应力的应力分布

偶应力理论的平衡方程为：

其中：重复出现的下标i、j和k分别取值1、2、3；下标“，”表示对其后坐标求偏导；fj和mj分别为单元的体力和体力偶；ejkl为排列算子。

几何方程为：

其中，ωj为转角分量。

静力边界条件为：

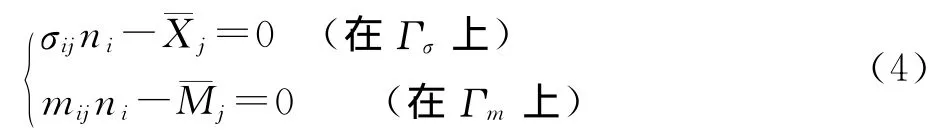
位移边界条件为：

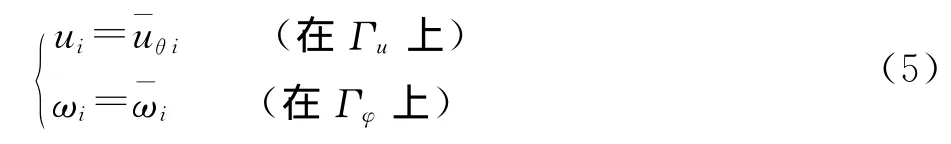
其中：ui为边界位移分量；为已知边界与水平方向夹角为θ的方向上的位移；为已知的微转动位移。

如果把层状岩体的薄层考虑为连续均匀介质，偶应力理论只用来模拟薄层的弯曲效应，则只需考虑曲率变量中的κ1和偶应力变量中的m1，简化后的偶应力理论本构方程为：

上式中，广义应力应变分量定义为：

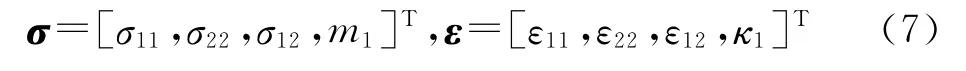
弹性矩阵为：

在式（8）中，

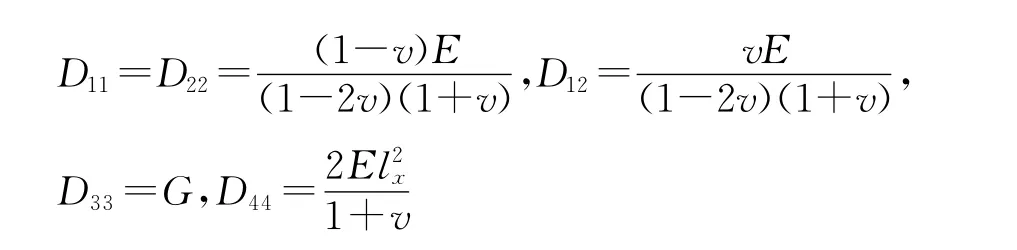
其中：E、v和G分别为弹性模量、泊松比和剪切模量；lx为材料的本征尺度，与岩体的节理间距有关。

2 无网格法数值计算框架

本文采用移动最小二乘近似构造具有高阶连续特征的形函数［11－12］，把Ω域上待求函数u（x）的近似函数uh（x）表达为：

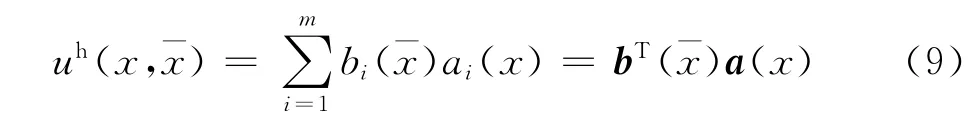
对于本文的平面问题，选用一维三次基函数：

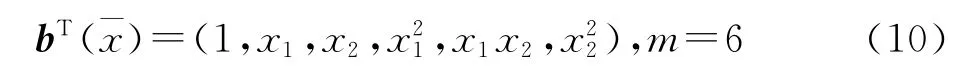
近似函数uh（x，）在x点邻域内的误差加权平方和为：

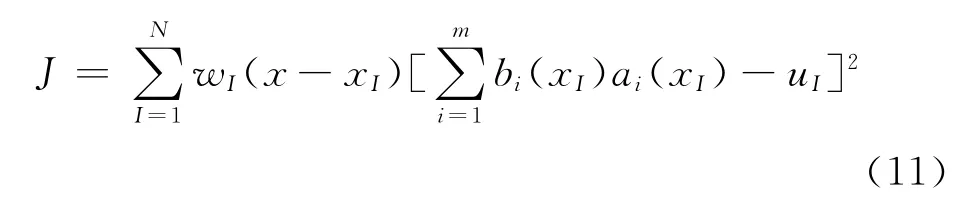
式中：wI（x－xI）是权函数，当x在xI影响域内部时，wI（x）＞0；当x在xI影响域的边界和外部时，wI（x）＝0，N为影响域内的节点数。

对式（11）求导得：

令

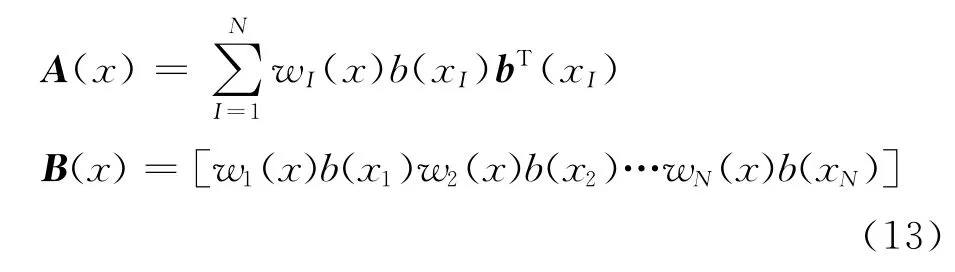
移动最小二乘法的形函数可以计算为［8－9］：

形函数的一阶导数可计算为：

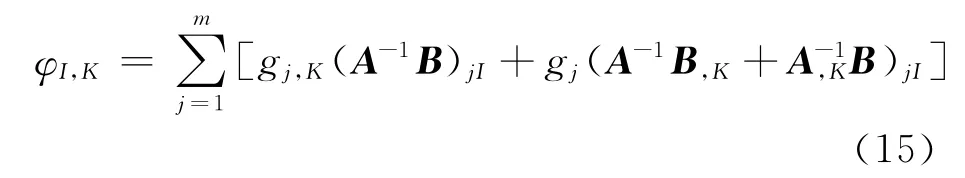
其中：

形函数的二阶导数可计算如下：

其中：

基于式（15）和式（16），应变和曲率均可直接由节点位移插值，由伽辽金法可以建立问题的无网格计算框架，刚度矩阵积分形式为：

其中：

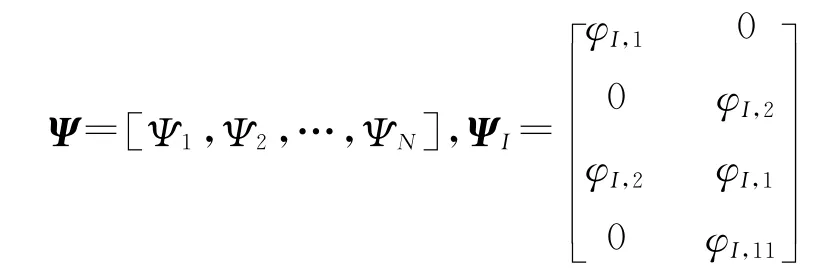
本文采用下列三级样条函数作为权函数：

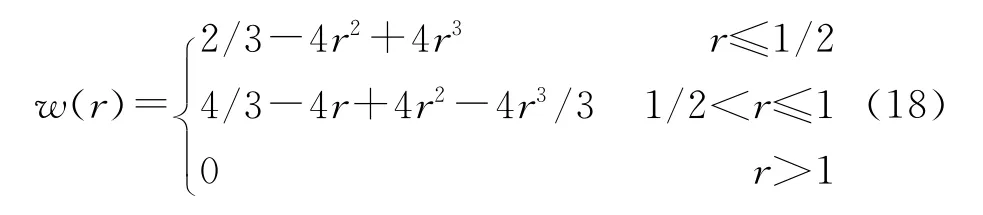
在计算刚度矩阵时，积分区间的布置与节点的布置分别独立进行，为了方便计算，本文中积分区间的布置与节点的布置一致（即相邻四节点确定一个积分区间，如图2），然后应用高斯积分对每个积分区间进行积分。通过求解下列方程组可以得到节点的位移：

其中，U为节点位移向量（不包含节点转角），F为节点力矢量。

由于位移、转角和曲率均由节点位移来插值，位移和转角边界条件均可采用罚数法施加。

3 地下洞室的数值模拟

图2 计算节点与高斯点布置示意图

上述的方法已经被作者用Fortran语言编写了计算程序，并对地下洞室进行了数值模拟。当把本征尺度lx取为零时，问题转化为传统各向同性介质的解，可以和有限元ANSYS软件的计算结果进行比较。层状岩体地下洞室模型如图3所示，问题被处理为平面应变问题，弹性模量E＝2．06×106MPa，泊松比v＝0．3，模型顶部无约束，左右两侧均约束竖直方向的位移，底部约束两个方向的位移。层状岩体中的水平地应力ξx＝－106MPa，竖向地应力ξy＝－5×105MPa，洞室内壁没有任何约束。在建立的模型上布置4个测点，测点位置如图3所示，无网格法计算模型节点布置如图4所示。

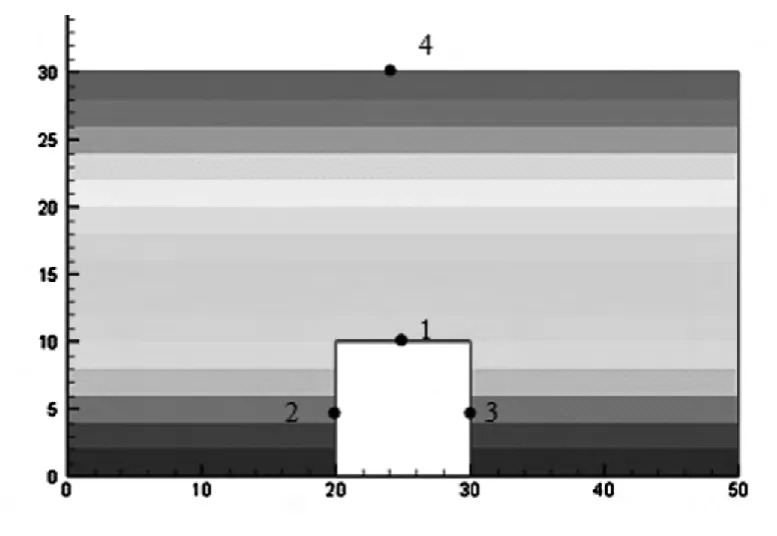
图3 层状岩体地下洞室模型

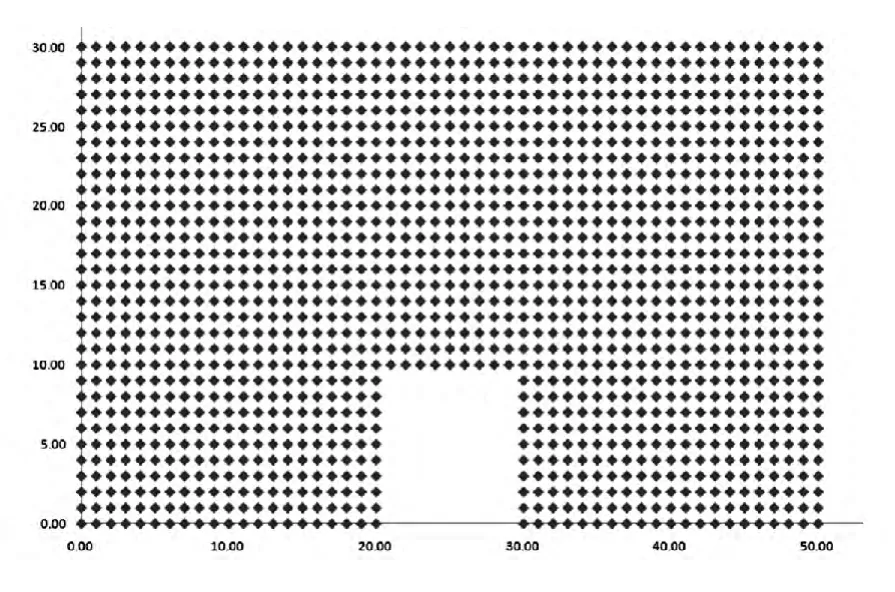
图4 无网格法计算模型节点布置图

用建立的无网格法计算框架对层状岩体地下洞室进行数值模拟，首先取尺度因子lx＝0，表1给出了4个测点竖直方向的位移，和ANSYS软件计算结果非常接近。图5给出了竖直方向的位移云图，与图6中的ANSYS软件计算结果非常接近。

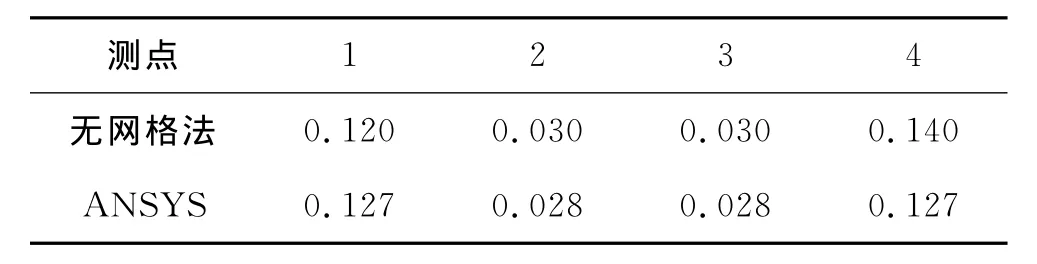
表1 层状岩体各测点竖直方向的位移m

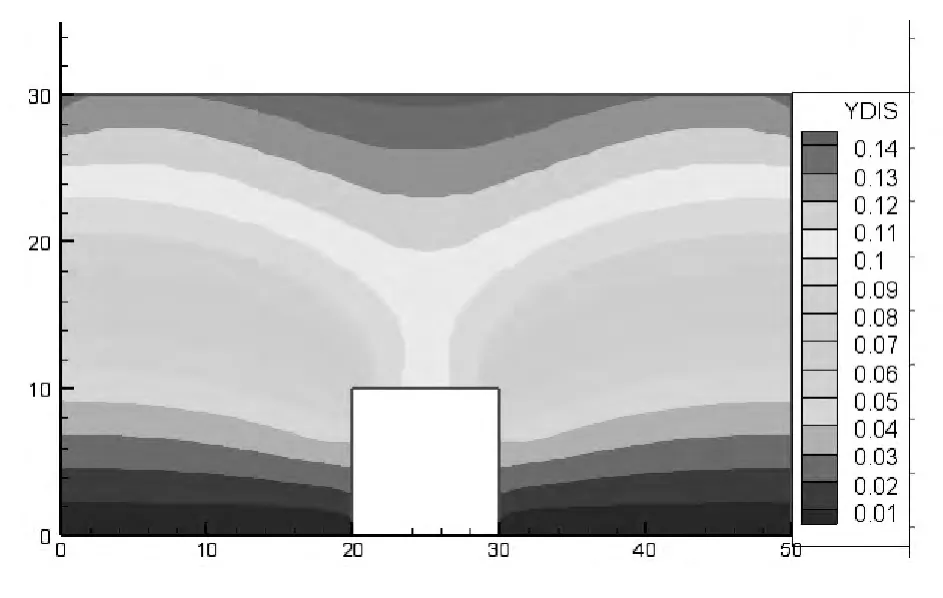
图5 无网格法数值模拟层状岩体地下洞室竖直方向位移云图

图6 ANSYS软件模拟层状岩体地下洞室竖直方向位移云图

由此可以看出，采用基于偶应力理论的无网格法与采用ANSYS有限元软件模拟得到的层状岩体地下洞室各测点的位移基本上一致，本文建立的数值计算框架可以获得比较好的效果。将节理层厚取t＝0．01 m，尺度因子取为lx，由无网格法得到应变云图如图7和图8所示。

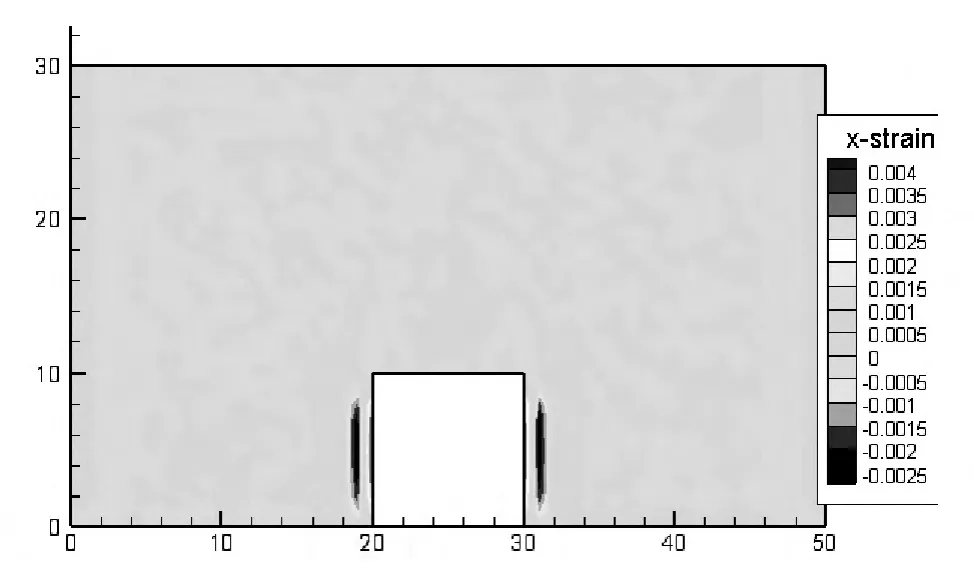
图7 无网格法数值模拟层状岩体地下洞室应变ε11云图

图8 无网格法数值模拟层状岩体地下洞室应变ε22云图

特征尺度因子可以取为节理间距，基于尺度因子建立高阶的连续结构模型，可以很好地反映其固有特性。下面变化尺度因子，研究其对计算结果的影响。让尺度因子lx在0．01 t～20 t之间变化，地下洞室1点竖直方向位移相对于lx＝0时结果的变化如图9所示。可以看出，此尺度因子对计算结果有较大的影响，但是当lx达到一定值时，其影响逐渐收敛。所以，分析尺度因子的内在物理意义，确定其具体数值，是一个非常关键的问题。

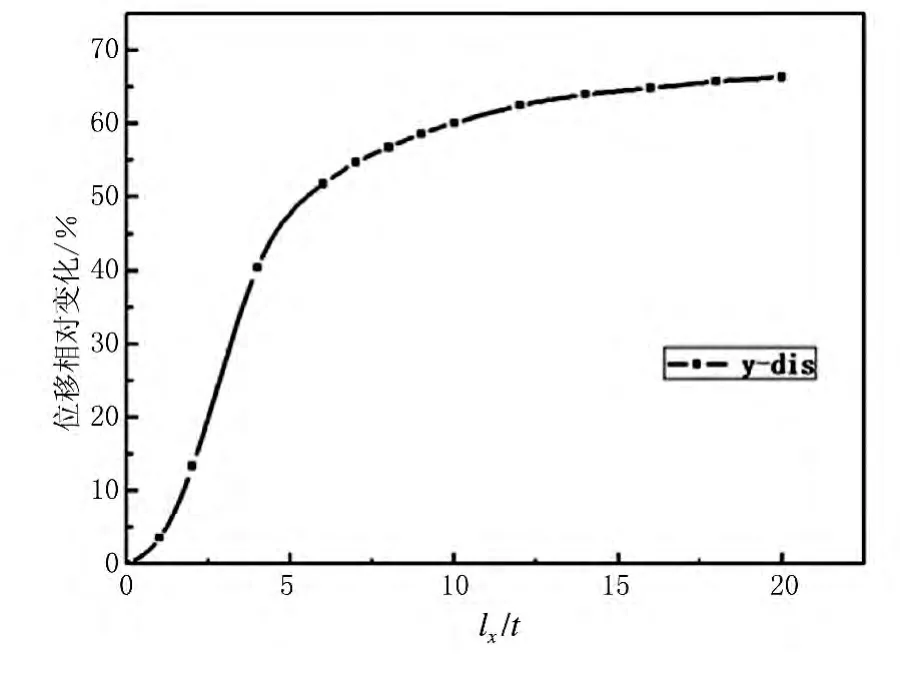
图9 尺度因子lx对竖直方向位移的相对影响

4 结 语

本文应用偶应力理论描述层状岩体的本构反应，应用移动最小二乘近似的形函数具有高阶连续的特点，应变和曲率直接由节点位移近似，建立的无网格数值框架中只有节点位移是未知量，方便进行数值计算。数值算例说明本文建立的数值计算方法非常有效。

偶应力理论可以描述层状岩体中薄层的弯曲效应，尺度因子与节理间距有关。本文分析了尺度因子的影响规律，通过选取适当的尺度因子数值对传统连续理论的结果进行修正，为岩土工程实际问题分析提供了参考。

［1］ 佘成学，熊文林，陈胜宏．具有弯曲效应的层状结构岩体变形的Cosserat介质分析方法［J］．岩土力学，1994，15（4）：12－19．

［2］ 佘成学，熊文林，陈胜宏．层状岩体的弹粘塑性Cosserat介质理论分析［J］．水利学报，1996（4）：10－17．

［3］ Ahikary D P，Muhlhars H B，Dyskin AV．Modelling the Large Deformations in Stratified Media－The Cosserat Continuum Approach［J］．Mechanics of Cohesive Frictional Materials，1999，4（3）：195－213．

［4］ Ahikary D P，Muhlhars H B，Dyskin AVA．Numerical Study of Flexural Buckling of Foliated Rock Slopes［J］．International Journal for Numerical and Analytical Methods in Geomechanics，2001，5（9）：871－884．

［5］ 刘俊，陈胜宏．节理岩体三维偶应力弹性理论［J］．岩土力学，1995，16（4）：20－30．

［6］ 刘俊，黄铭，葛修润，等．层状岩体开挖的空间弹性偶应力理论分析［J］．岩石力学与工程学报，2000，19（3）：276－280．

［7］ 李银平，杨春和．层状盐岩体的三维Cosserat介质扩展本构模型［J］．岩土力学，2006，27（4）：509－513．

［8］ 李银平，杨春和．具有弯曲效应的层状结构岩体变形的Cosserat介质分析方法［J］．岩土力学，1994，15（4）：12－19．

［9］ 杨乐，吴德伦，李德万，等．层状岩体的Cosserat介质均匀化［J］．应用力学学报，2010，1（27）：96－101．

［10］ 梁醒培，王辉．应用有限元分析［M］．北京：清华大学出版社，2003．

［11］ Belytschko T，Krongauz Y．Meshless Method：an O－verview and Recent Developments［J］．Computer Method in Applied Mechanics and Engineering，1996，139（1－4）：3－47．

［12］ Sun Y Z，Liew K M．Bending Buckling of Single－walled Carbon Naotubes：Higher Order Gradient Continuum and Mesh－free Method［J］．Computer Method in Applied Mechanics and Engineering，2008，197：3001－3013．