厚向强度分布对特厚板三辊预弯成形的影响

仉志强，付建华，宋建丽，金坤善，李永堂

(太原科技大学 材料科学与工程学院，太原030024)

0 引 言

厚向材料特性分布是影响板材弯曲的重要因素。Hoggan 等［1］发现经过表面精轧的低碳回火板带屈服应力下降50%。Weiss 等［2］发现由冷轧产生的厚向残余应力会软化薄铝板并降低弹塑性转变弯矩。

目前采用重型卷板装备的特厚板弯卷成形工艺已应用于石油、化工和风电等重要行业，具有节能省材和效率高等优点。用于弯卷工艺的特厚板在生产时经过多道轧制和热处理工艺，厚向材料强度和硬化特性呈现较大差异。Fujii 等［3］在98 mm 的SM570 板材厚向多位置进行采样并试验，发现厚向屈服应力和残余应力差异均很大，自内向外屈服应力增幅达60%。由文献［1-2］可知，这种厚向强度不均匀分布特性必然会影响板材预弯成形，增大现有板材预弯工艺模型的计算误差。板材弯卷成形研究成果较多，主要侧重于中厚板滚弯成形［4-6］，而针对预弯成形方面的研究较少。Hua 和Lin［7］研究了材料硬化指数对中厚板四辊预弯成形的影响，胡卫龙［8］建立了薄板三辊预弯成形理论模型。目前仍鲜有研究和建立厚向材料特性分布对板材预弯成形影响的理论模型。本文将建立厚向强度线性分布的特厚板三辊预弯模型，一方面可以提高预弯成形力和弯矩计算精度，满足卷板装备设计要求;另一方面可以降低上辊压下量和预弯角等几何参数预估误差，提高成形精度和效率。

1 试验方法及结果

1.1 试验材料及方法

厚向强度分布试验选用100 mm×2000 mm、220 mm×2000 mm 的Q235 热轧板。如图1 所示，在板材厚向多个等间距分布位置切取圆棒试样，试样截取位置距侧面距离Wd＞500 mm，试样轴线与轧制方向平行，每个位置样本数为2，总样本数为28。利用100 kN 的WAW-E100 丝杠驱动微控机对试样进行静拉伸试验，配有位移传感器检测试样两端夹具移动，拉伸速度约2 mm/min，分辨精度为0.001 mm。

1.2 试验结果

试验板材表层和中心层附近试样的真实应力-应变(σ-ε)曲线如图2 所示。可以看出，两种特厚板不同厚度位置的应力-应变曲线在弹性区接近重合，杨氏模量约为205 GPa;每种板材厚向不同位置的应力-应变曲线在塑变区内近乎平行。板材厚向屈服应力(σs)分布如图3 所示，z 为取样点距中间层的垂直距离，t 为板厚。可以看出，板材表层材料屈服应力大，中间层屈服应力小，自内向外屈服应力符合二次抛物线分布，屈服应力增量分别为35、61 MPa，增幅分别为14%和26%。

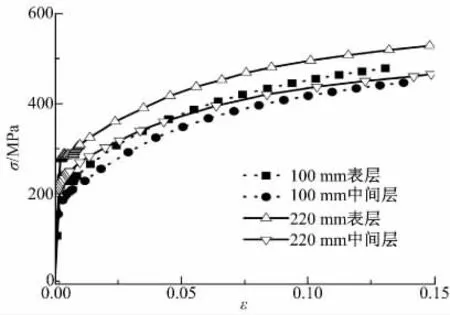
图2 两种板材不同位置的应力-应变曲线Fig.2 True tress-strain curves for the two plates

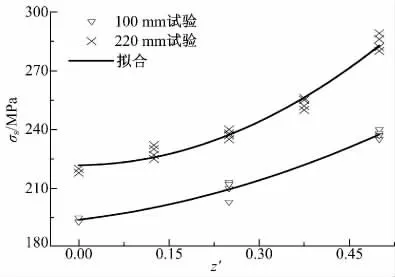
图3 厚向屈服应力试验数据分布和二次拟合曲线Fig.3 Experimental data of yield stress and fit curves

2 数学模型

2.1 应力-应变建模

考虑厚向强度分布的应力模型满足如下假设条件:

(1)根据“板层分析法”将板材等分为若干层，假设同一板层内材料屈服应力相等。任一板层材料屈服强度σs(z)与该层至中间层垂直距离z 有关。

(2)假设材料屈服应力由表层向中间层线性减小(见图4)。那么反映强度分布的系数β 为:

距中间层z 的板层材料屈服应力为:

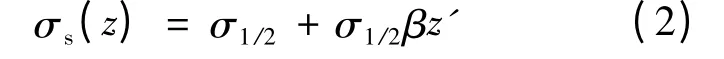
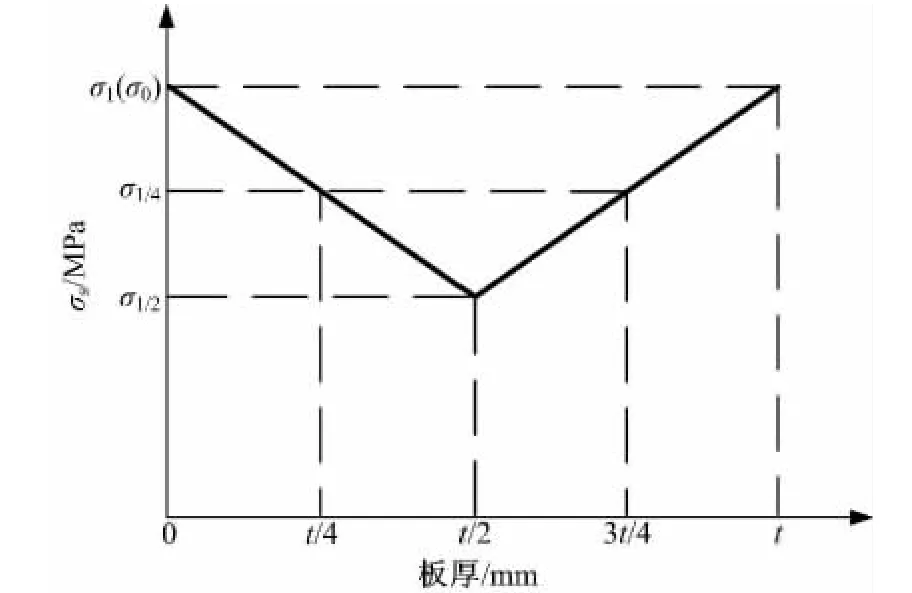
图4 板材厚向屈服应力线性分布曲线Fig.4 Linear yield stress distribution through thickness

(3)不同板层内材料的弹性模量相等，塑变范围内各板层材料符合指数型强化模型，图5 中曲线Ⅰ，Ⅱ，Ⅲ分别表示上(下)表层、t/4 层和中间层的硬化曲线，且曲线相互平行。

图5 厚板弹塑性材料应力应变曲线Fig.5 Stress-strain curves of different material layers

厚向强度线性分布的材料应力-应变模型为:

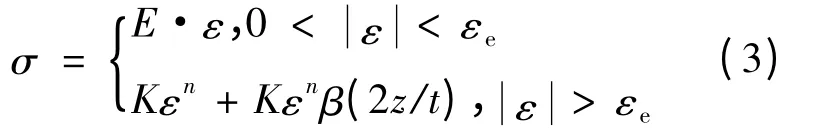
式中:E 为杨氏模量;K 为硬化系数;n 为硬化指数;z'=2z/t。

2.2 弯矩-曲率建模

(1)弹性弯曲

依据塑性弯曲工程理论，板材弹性弯矩为:

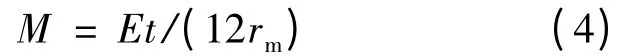
式中:r 为与中间层平行的任一板层半径;rm为中间层半径为相对曲率;M 为弯矩。

(2)弹塑性弯曲

如图6 所示，板材内、外侧的阴影区内材料发生塑性变形，中间区材料为弹性变形，图中，ri为弯板内径;ry为弯板外径。将代入ε=r/rm－1，整理得到弹性区内、外层半径rei和rey。

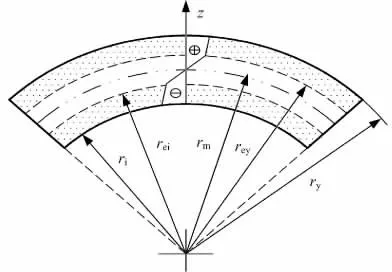
图6 中厚板弹塑性弯曲时的三个变形区域Fig.6 Three zones of plate in elastic-plastic bending

那么弹性变形区弯矩为:

式中:εe为材料弹性应变极限。

板材弹塑性弯曲时的弯曲相对曲率较小，材料单元纵向应力远大于径向应力，根据平面应变和不可压缩假设得到材料单元承受的纵向应力为［9］:

式中:σθ为纵向应力;为等效应力。

当rey＜r ＜ry时，外侧塑性变形区的弯矩为:

那么弹塑性弯曲总弯矩为:

根据板材回弹工程理论，回弹前、后半径满足:

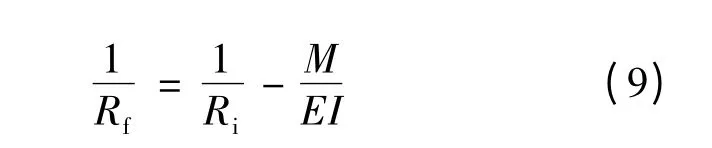
式中:Ri为回弹前半径;Rf为回弹后半径;I 为截面系数，I=Wt3/12，W 为板材宽度。

2.3 预弯成形建模

图7 为板材三辊预弯成形和弯距分布示意图。上工作辊为动力输出辊，其中心与对称线PP'的偏距为e，沿y 轴压下使板材弯曲。三辊预弯建模的假设条件为:预弯成形为准静态过程;工作辊为刚性辊。图7 中板材弯曲段AB 的外部弯距呈线性分布，力矩最大值位于点B，记为MB;弯曲段AB 包含弹性变形段(AE 段)和弹塑性变形段(EB段)。

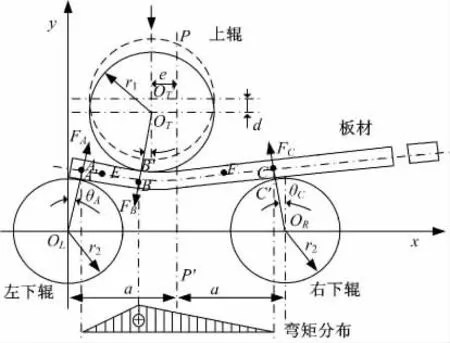
图7 三辊压弯工艺和弯矩分布示意图Fig.7 Diagram for pre-bending and moment distribution

当xA≤x ≤xE时，板材弹性弯曲曲率为:

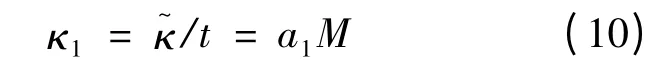
当xE≤x ≤xB时，曲率采用近似多项式表示:

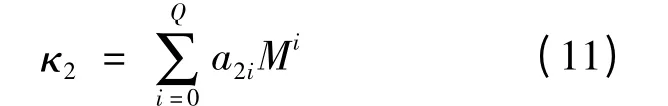
因为板材发生弹塑性弯曲，且曲率最大点B处曲率(y')2≪1，所以板材曲率可近似表示为:

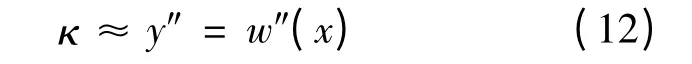
当xE≤x ≤xB，将式(10)代入式(12)，积分得:

式中:G=MB/(xB－xA)。

将式(13)积分可得:

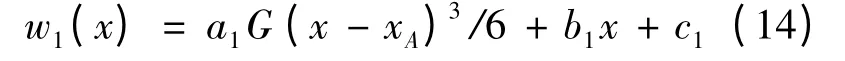
同理，当xE≤x ≤xB时:

同理，当xB≤x ≤xF时:

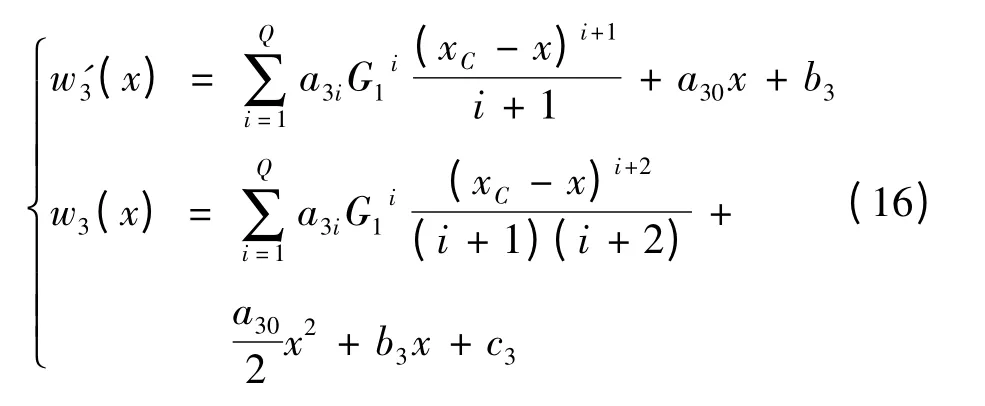
式中:G1=MB/(xC－xB)。

同理，当xF≤x ≤xC时:

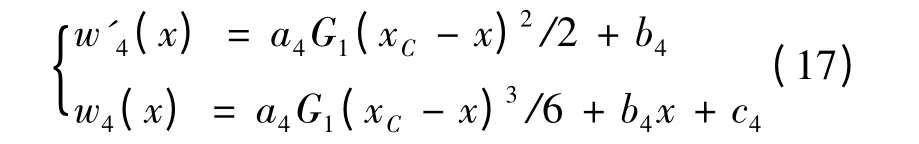
式(12)～(17)中未知系数ai、a2i、a3i、bi、ci(i=1，2，3，4)通过点A、E 和B 处的边界条件确定。采用Matlab 求解模型。通过建立力学平衡式确定上辊压下力与接触角间的关系:

式中:FB、FA、FC分别为上辊和左、右下辊受力;FAy、FCy为左、右下辊垂直力;μ 为板材与工作辊的摩擦因数;θA和θC为板材与下辊的接触角;a为两下辊间距的一半;r1为上辊半径;r2为下辊半径。

3 计算结果及比较

针对长治锻压和太原科技大学合作研发的重型三辊卷板机CDW11XNC-300420×2500 mm 预弯成形工艺进行理论计算，各结构参数及相应数据如下所示:e 为300 mm;W 为1000 mm;t 为100，220 mm;n 为0.15;K 为597;E 为205 GPa;σs为235 MPa;a 为850 mm;r1为700 mm;r2为425 mm。采用Abaqus/Explicit 动态算法对三辊不对称预弯工艺进行有限元模拟计算。接触边界和网格划分等步骤中主要参数设置如下:工作辊为解析刚体;工作辊与板材接触摩擦因数为0.2;上工作辊为驱动辊，下降速度为1 mm/s;板材厚度、长度和宽度网格数分别为10、80 和10。

回弹比η(η=Rf/Ri)是用于反映板材回弹特性的重要参数。如图8 所示，每种板材η-R 曲线的η 值随曲率半径R 增大而单调递增，表明曲率半径越大，板材回弹特性越好;当β 取不同数值时，每种板材的三条η-R 曲线随半径增大而逐渐发散，表明厚向强度分布对板材回弹的影响随半径增大而增大。如图8 所示，当Rd=6 m 时，100 mm 板材的回弹比为1.35;220 mm 板材的回弹比为1.05。当β 值增量为0.1 时，100 mm 和220 mm 板材的回弹比增量均小于0.05，厚向强度分布对板材回弹影响远小于板厚影响。

厚向强度分布对板材预弯成形的影响体现在力学和几何参数两方面。图9 为上辊卸载回弹前厚向强度系数(β=0，0.1，0.2)不同时，板材与辊接触角θA、θC和预弯角θ(θ=θA+θC)与上辊压下位移的关系曲线。可以看出，随着上辊压下位移d 增大，不同β 值的同种角度曲线几乎完全重合，表明厚向强度分布对卸载前的预弯角并无明显影响。由图8 可知，β 值越大，回弹比越大，因此卸载回弹后的预弯角也会越大;那么制定特厚板三辊预弯工艺时，板材厚向强度分布系数越大，上辊压下位移就越大。

图9 上辊压下位移与预弯角的关系曲线Fig.9 Curve of top-roller displacement verses bending angle

图10 不同厚度的特厚板预弯时的力学结果Fig.10 Force results of super-thick plate prebending for different thickness

图10 为不同厚度的特厚板预弯时的力学结果。图10(a)中曲线A、B、C 分别为强度分布系数β=0、0.1、0.2 的100 mm 厚板预弯时上辊作用力与压下位移间的理论曲线，可以看出，随着厚向强度不均匀程度增大(即β 增大)，上辊力逐渐增大，图10(a)中数值模拟曲线与理论曲线A 比较吻合，验证模型正确。采用ΔF/F 表示β≠0 时上辊力相对于β=0 时上辊力的变化率。如图10(b)所示，对于任一β 值，ΔF/F 在弹性变形阶段(0 ＜d ＜5 mm)为0，在弹塑性转变点附近(d≈5 mm)突然增大，在弹塑性变形阶段(5 mm ＜d ＜65 mm)接近恒定值;对于不同β 值，ΔF/F(图10(b))随β 增大而成比例单调递增，当β=0.1 时，ΔF/F≈0.068;β=0.2 时，ΔF/F≈0.136。经分析，ΔF/F 曲线在弹性阶段和弹塑性转变时的变化趋势由2.1 节假设条件(3)造成，而弹塑性阶段ΔF/F 变化趋势的影响因素很复杂。由弯矩力臂公式F=M/L 可推出公式(ΔF+F)=(ΔM+M)/(ΔL+L)(L 为力臂;ΔL 为由β 值引起的力臂变化量)。图10(b)中，当d 为定值时，ΔF/F 随β增大而成比例增大，这是因为:①力臂L 几乎不受β 值影响，即ΔL≈0，这可根据图9 中β 值对卸载前预弯角几乎没有影响的结论推断出来;②ΔM/M 随β 值增大而成比例增大，这可根据特厚板总弯矩公式(式(8))求解。图10(b)中，β 值一定时，ΔF/F 随d 的增大而近乎恒定，主要由三方面因素共同作用:①由于工作辊半径较大，上辊与板材接触点两侧力臂L 随着d 的增大会发生较大变化，且接触点的偏距e 也会增大，如图7 所示。②ΔM/M 随d 值增大而逐渐减小。③随着预弯角θ的增大，左、右下辊水平分力FAx、FCx会增大并相互抵消，降低了上辊的作用力。

由图10(c)可以看出，当d=20 mm 时，曲线B 与A、C 与B 间预弯力增量ΔF=0.5 MN，与之对应的100 mm 板预弯力增量ΔF=0.3 MN(见图10(a))，所以板材厚度较大时，上辊垂直力增量ΔF 较大。通过图10(b)和10(d)对比看出，板材厚度不同时，相同β 值对应的力变化率ΔF/F 几乎相等。由文献［3］和第1 节中试验数据可知，越是较厚的板材，厚向强度不均匀程度越大。所以，板材厚度越大，ΔF/F 越大，越应重视厚向强度分布对工作辊作用力的影响;上辊压下量越大，力增量ΔF 越大，越应考虑厚向强度分布的影响。

4 结束语

通过特厚板厚向多位置采样试验及预弯工艺研究，建立了厚向强度分布对预弯力、力矩、预弯角和接触角等参数的影响模型，研究结果表明:特厚板厚向强度的非均匀分布显著增大特厚板弯曲力矩、工作辊受力，回弹比略有增加，但对卸载前预弯角等几何参数并无明显影响，这将为卷板机强度、刚度设计和特厚板预弯工艺制定提供更准确的数据支持。

［1］Hoggan E J，Scott R I，Barnett M R，et al.Mechanical properties of tension leveled and skin passed steels［J］.Journal of Materials Processing Technology，2002，125-126:155-163.

［2］Weiss M，Rolfe B，Peter D H，et al.Effect of residual stress on the bending of aluminium［J］.Journal of Materials Processing Technology，2012，212(4):877-883.

［3］Fujii K，Ishikawa S，Nakamo Y.Materials properties and residual stresses of rolled thick plate and their effect on static strength［J］.Doboku Gakkai Ronbunshuu A，2010，66(2):253-263.

［4］Hansen N E，Jannerup O.Modeling of elastic-plastic bending of beams using a roller bending machine［J］.J Eng Ind，1979，101(3):304-310.

［5］Shin J G，Park T J，Yim H.Kinematics based determination of three rolling region in roll bending for smoothly curved plates［J］.J Manuf Sci Eng，2001，123(2):284-290.

［6］Gandhi A H，Raval H K.Analytical and empirical modeling of top roller position for three-roller cylindrical bending of plates and its experimental verification［J］.Journal of Materials Processing Technology，2008，197(1):268-278.

［7］Hua M，Lin Y H.Effect of strain hardening on the continuous four-roll plate edge bending process［J］.Journal of Materials Processing Technology，1999，89(1-3):12-18.

［8］胡卫龙.板材弯卷变形的理论分析与实验研究［D］.哈尔滨:哈尔滨工业大学机电工程学院，1992.Hu Wei-long.The theoretical analysis and experimental study of the plate roll bending［D］.Harbin:School of Mechatronics Engineering，Harbin Institute of Technology，1992.

［9］Wang C T，Kinzel G，Altan T.Mathematical modeling of plane-strain bending of sheet and plate［J］.Journal of Materials Processing Technology，1993，39(3-4):279-304.