基于跟驰数据采集分析的各异性跟驰模型

敬 明，王 昊，王文静

(1.交通运输部公路科学研究院，国家智能交通系统工程技术研究中心，北京100088;2.交通运输部公路科学研究院，智能交通技术交通行业重点实验室，北京100088;3.东南大学 交通学院，南京210096)

0 引 言

交通流中车辆和驾驶员的个体差异导致跟驰行为中车辆的轨迹不一致，反映到交通流跟驰模型中，表现为不同车辆的参数标定结果出现差异。依据车辆跟驰数据对跟驰模型参数进行标定和分析是将交通调查数据与车辆和驾驶员特性联系起来的方法之一。Newell 于2002 年提出一个简化的跟驰模型，模型中只包含两个参数，但是可以提供足够的仿真精确度［1-2］。该模型的提出隐含了一个观点，即通过两组相互独立的变量就可以描述车辆和驾驶员在跟驰行为中的特性。文献［3-4］对调查采集的跟驰数据直接进行因子分析，并用4 个因子来描述车辆和驾驶员的特性，其中前3 个因子提供的信息量约占据信息总量的95%。许多经典跟驰模型方程中含有数量较多的参数，例如智能驾驶模型(Intelligent driver model，IDM)方程中有7 个参数。如果只需要4 个或更少的因子就可以描述车辆和驾驶员特性，则模型的参数间可能存在一定的相关关系，通过分析模型参数在不同个体间的变化规律，可以将参数归纳为数量更少的因子，从而简化描述车辆和驾驶员的个体特征。文献［5-8］对各异性跟驰模型进行了研究，但是在描述个体特征时，没有考虑到模型参数间的相关性，参数都以相互独立的方式离散，并且也没有进行跟驰数据的采集分析工作。

本文在上述研究的基础上，提出了一种基于跟驰数据研究车辆和驾驶员特性分布的方法，以优化速度模型(Optimal velocity，OV)［9］和IDM 模型［10］为例，基于模型参数的相关性提出了特征因子的概念，根据跟驰模型参数取值研究了特征因子(即车辆和驾驶员特性)的分布情况。在已知特征因子分布时，通过特征因子与模型参数的换算建立了各异性IDM 模型，实现了对异质交通流的仿真分析。

1 车辆跟驰数据的采集和处理

1.1 跟驰数据采集

在江苏省南京市，于天气晴朗的工作日下午14∶ 00 ～17∶ 00，沿龙蟠中路-瑞金路-御道街-中山东路-龙蟠中路的路线，采用跟车调查的方法，使用车载激光测速测距一体化系统采集了25 位驾驶员(包括16 位专业驾驶员和9 位业余驾驶员)所驾驶车辆在沿全程路线行驶过程中的速度和车辆间距信息。数据采集系统包括:车载激光测距仪一台，GPS 一个，处理机一台。其中GPS用来测量试验车速度;车载激光测距仪用来测量试验车与前车的间距。对于每个驾驶员，采集的原始数据以矩阵形式存储，矩阵的第1 列为时间(时间步长为0.1 s);第2 列为本车的速度;第3列为本车与前方车辆的间距。

1.2 数据筛选和平滑处理

车辆和驾驶员在加速、减速的行驶过程中会体现出不同的跟驰特性，因此筛选出对应不同行驶状态的跟驰数据，并在此基础上分别进行参数标定。

设采集到的第i 个驾驶员的数据矩阵Di共有a 行3 列，根据时间、速度和车辆间距初步将数据分段:对于数据组中任意一行k(0 ＜k ≤a－1)，如果Di(k+1，1)－Di(k，1)≥1，即时间突变超过1 s，说明采集计时出现间断;如果Di(k+1，2)－Di(k，2)≥1，即速度突变超过1 m/s，说明采集计时可能出现间断;如果Di(k+1，3)－Di(k，3)≥3，即间距突变超过3 m，说明前方车辆换道或者采集计时出现间断，则在k 行后添加分隔符将数据分开。

将Di中时间持续时长≥10 s 的数据段进行保留，将其他数据删除，从25 个驾驶员的数据中得到509 个数据段。数据筛选条件针对跟随同一辆前车的车辆行驶过程，得到的数据组可以描述车辆的跟驰状态，记为

对Di中的速度数据进行差分计算出车辆加速度，从加速度为正值时开始记录时间长度，如果加速度出现0 或负值并且持续时间超过1 s，则终止记录，记录的时长t=te－ts－tm，te为结束记录的时间;ts为开始记录的时间;tm为终止条件中加速度为负数或0 状态持续的时间。如果记录时长≥6 s，则对该数据段进行保留，将不符合条件的数据删除，从25 个驾驶员的数据中得到137 个数据段。数据筛选条件针对跟随同一辆前车的车辆行驶过程中本车加速度大于0 的情况，得到的数据组可以描述车辆的加速状态，记为

对Di中的速度数据进行差分计算出车辆加速度，从加速度为负值时开始记录时间长度，如果加速度出现0 或正值并且持续时间超过1 s，则终止记录，记录的时长t=te－ts－tn，tn为记录终止条件中加速度为正数或0 状态持续的时间。如果记录时长≥6 s，则对该数据段进行保留，将不符合条件的数据删除，从25 个驾驶员的数据中得到285 个数据段。数据筛选条件针对跟随同一辆前车的车辆行驶过程中本车加速度小于0 的情况，得到的数据组可以描述车辆跟驰过程中的减速状态，记为

1.3 跟驰模型参数标定

式中:k 为灵敏度参数;v(xn－1(t)－xn(t))为由车辆间距决定的优化速度，本文采用Helbing 与Tilch 提出的优化速度方程［12-13］为:

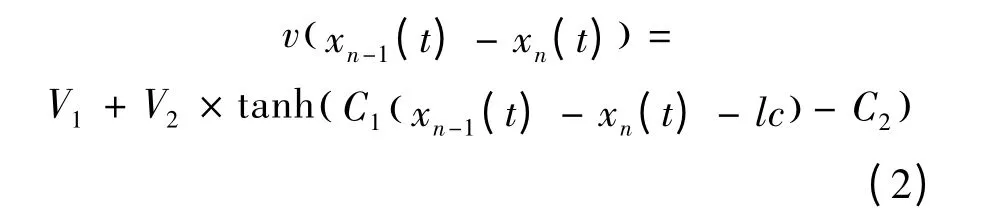
式中:lc 为车身长度，V1、V2、C1、C2为相关参数。

IDM 模型的表达式为:

式中:Δv(t)为本车与前车的速度差;s*(vn(t)，Δv(t))为当前状态下驾驶员的期望间距;w 为起步加速度;d 为舒适减速度;δ 为加速度指数;v0为车辆的理想速度;s0为静止安全距离参数;s1为与速度相关的安全距离参数;T 为驾驶员在刹车时需要的反应时间。

对于式(4)，当两车速度差为较大负值时，会产生负的期望间距，而在式(3)中负的期望间距会被当做正值来处理，产生错误，因此本文通过式(5)对期望间距进行修正。

参数的标定过程采用最小二乘法，算法的目标是使下述目标函数取最小值:

式中:time 为数据段包含的时间长度;vn(t)、分别为t 时刻实测速度和根据拟合参数计算的速度;分别为t 时刻实测车辆间距和根据拟合参数计算的车辆间距。

为了达到较好的标定效果，目标函数中综合考虑了车速和车辆轨迹的拟合。由于加入time－1项，计算的残差是时间段内速度和位移的拟合差值在每个时间步内的平均值，这样便于进行时间长度不同的数据段之间的比较。

根据数据组的数据分别对OV 模型和IDM 模型进行参数标定。如果对于驾驶员n，在加速过程筛选出k 个数据段，得出了k 组参数标定结果，则该驾驶员对应加速过程的参数标定结果为:

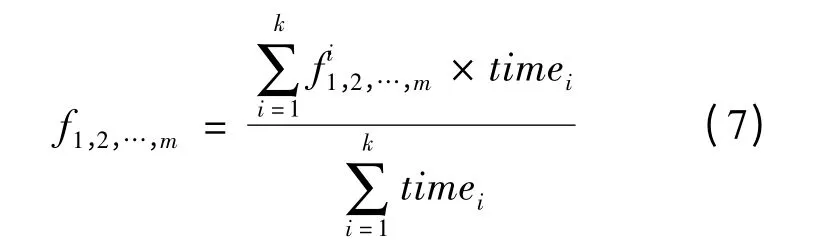
式中:f1，2，…，m表示模型第1，2，…，m 个参数的标定结果表示通过加速过程第i 段数据标定的模型第1，2，…，m 个参数。

由于数据段包含的时间越长，越能代表驾驶员的行为特征，所以在计算参数平均值时将第i段数据包含的时长timei作为该数据段标定参数的权重。根据相同方法对减速状态和跟驰状态数据的标定结果进行处理，得到矩阵BDac、BDdc和BDnor，分别为根据加速、减速和跟驰状态数据得出的参数标定结果，对应的残差平均值分别为1.9926×10－4、7.6433×10－4和4.2588×10－4。参数标定结果都为25×12 阶矩阵，矩阵的每一行代表一个驾驶员的参数标定结果，第1 ～5 列分别对应OV 模型参数k、V1、V2，C1，C2;第6 ～12 列分别对应IDM 模型参数w、v0、δ，s0，s1，T，d。

2 基于跟驰数据的车辆和驾驶员特性分析

由于车辆和驾驶员具有个体特征，不同的驾驶员在车辆跟驰过程中采取的行为方式存在差异，反映到跟驰模型中，体现为模型的参数具有不同的取值。为了研究模型参数在不同车辆间的变化规律，对各个驾驶员的参数标定结果进行主成分分析、因子分析和相关分析，结果表明相关分析的效果较好，同一模型的参数间相关关系较为明显，因此本文仅介绍相关性分析的过程:对BDac、BDdc和BDnor中的列向量进行相关分析，计算每两个列向量间的相关系数，设有第i 列和第j 列参数向量，则相关系数的计算公式为:

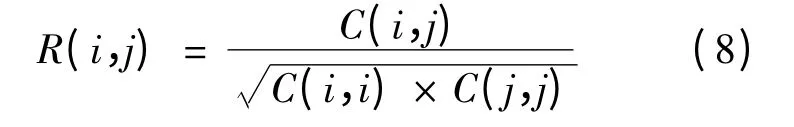
式中:C(i，j)为i，j 的协方差;R(i，j)为标准化的随机向量和的协方差。

假设满足相关系数R(i，j)＞0.7 或者R(i，j)＜－0.7 的向量是显著相关的，考查BDac、BDdc和BDnor内模型不同参数间变化的相关性，得出如下结论:①不同模型的参数变化相关程度并不明显;②同一模型内的参数变化有比较强的相关性。根据BDac得出，OV 模型中的参数V1和C1，V2和C2具有显著相关性，IDM 模型中的参数δ、s1、d 具有显著相关性;根据BDdc得出，OV 模型中的参数V2和C2具有显著相关性，IDM 模型中的参数v0和s0，w、δ、s1、d 具有显著相关性;根据BDnor得出，OV 模型中的参数V1和C1，V2和C2具有显著相关性，IDM 模型中的参数v0和s0，δ、s1、d 具有显著相关性。由于相关系数阈值取值较大，考虑到车辆行驶过程中随机因素的影响，对在加速、减速或跟驰状态中出现一次显著相关的参数即认为其具有显著相关关系。根据上述方法，OV 模型中的参数可根据相关情况分为3 组:k，V1和C1，V2和C2。其中V1和C1成负相关关系，而V2和C2成正相关关系。IDM 模型中的参数也可分为3 组:T，v0和s0，w、δ、s1、d。其中v0和s0，w、δ、s1、d 均成显著的正相关关系。

在描述车辆跟驰状态参数标定结果的矩阵BDnor中，模型参数在驾驶员间的变化情况如图1和图2 所示(考虑到图形的直观清晰，以两个参数为一组作图)。

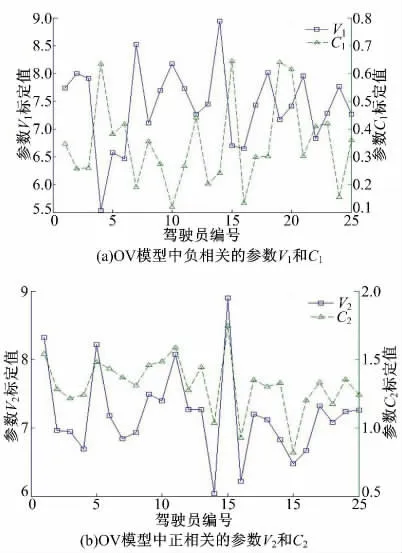
图1 OV 模型中显著相关的参数Fig.1 Significantly related parameters in OV model

在OV 模型和IDM 模型中，参数都可以依据相关分析分为3 组。在不同驾驶员间，同一组内的参数有着高度相关的变化方式，而不同组间的参数变化相关关系并不显著，因此本文假设三组参数分别对应车辆和驾驶员的三种特性，而不同的特性之间相互独立。由于跟驰模型中，车辆的个体差异性完全由参数取值来体现，本文用三个相互独立的因子来描述车辆与驾驶员在跟驰行为中的特性，称这些因子为特征因子。相关分析表明特征因子对应的参数变化是高度相关的，考虑到判定显著相关系数阈值取值较大、驾驶行为的随机性和参数采集标定过程中产生的误差，本文假设特征因子对应的相关参数间的变化方式是近似一致的(即参数的相关系数为1 或－1)，而不同特征因子对应的参数相互独立。当参数列i，j的相关系数为1 或－1 时，标准化的随机向量(i－和相等或互为相反数，据此提出特征因子的计算公式为:

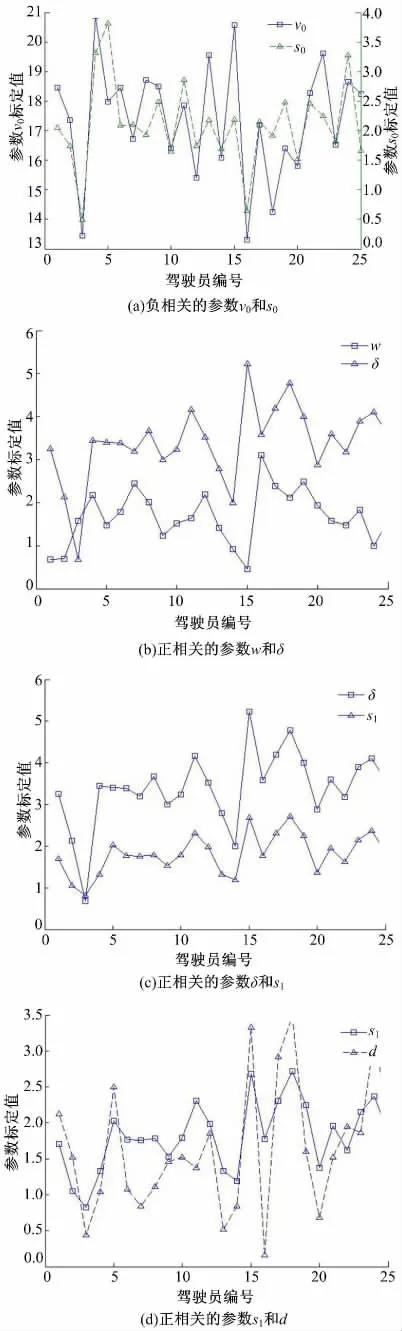
图2 IDM 模型中显著相关的参数Fig.2 Significantly related parameters in IDM model

式中:fi表示由第i 组具有相关关系的参数所决定的特征因子;n 表示第i 组参数所包含的参数个数;kij为参数组i 中第j 个参数;meankij表示样本数据中kij的均值;stdkij表示样本数据中kij的标准差。

由式(9)可知:每个特征因子都是一个随驾驶员编号变化的、标准化的随机变量。特征因子和具有相关关系的参数组是一一对应的，在已知特征因子和参数在样本中的均值和标准差的情况下，可以计算出具有相关关系的参数组中的参数值，方便特征因子在仿真过程中的应用。表1 给出了由描述车辆跟驰状态的参数标定结果矩阵BDnor得出的特征因子取值，表中OV 模型的特征因子对应参数对应参数V1和对应参数V2和C2。IDM 模型的特征因子对应参数w、δ、s1、d对应参数v0、s0对应参数T。

由于OV 模型和IDM 模型的特征因子都可以完整地描述车辆和驾驶员的跟驰特性，可以设想，存在可逆的向量函数g，使得，以及，即不同模型的特征因子之间可以相互转换，由于该转换关系并没有重要的实际应用意义，本文对其暂不进行深入研究。

IDM 模型的参数含义较为明确，因此根据IDM 模型的参数来考查该模型特征因子的实际意义。IDM 模型中与w、δ、s1、d 正相关，可见与车辆的加减速性能以及车辆在运动状态中与速度有关的安全距离选取有较为重要的联系，称为动态特征因子;与v0和s0正相关，其中v0和s0都与车辆的运动状态无关，因此称为静态特征因子;与参数T 正相关，称为反应时间特征因子。

了解特征因子的意义后，可以通过特征因子的取值考查车辆和驾驶员的特性及其分布，如表1 中1 号驾驶员的动态特征因子为－0.3524，静态特征因子为0.2339，反应时间特征因子为0.8704，可知该驾驶员驾驶的车辆加减速性能低于样本平均水平，同时驾驶行为比较谨慎，在车辆静止时采取较大的安全间距，在刹车时具有较长的反应时间。应当指出的是，不同模型得出的特征因子具有不同意义，对于某些模型，特征因子的含义也许难以表述，因此在研究车辆和驾驶员特性时，最好采用参数意义较为明确的模型进行标定和分析。通过对特征因子的分析可得出车辆及驾驶员的特性分布情况，由于条件所限，本文中数据样本量较少，因此对数据样本中车辆和驾驶员的特性分布暂不进行深入研究。

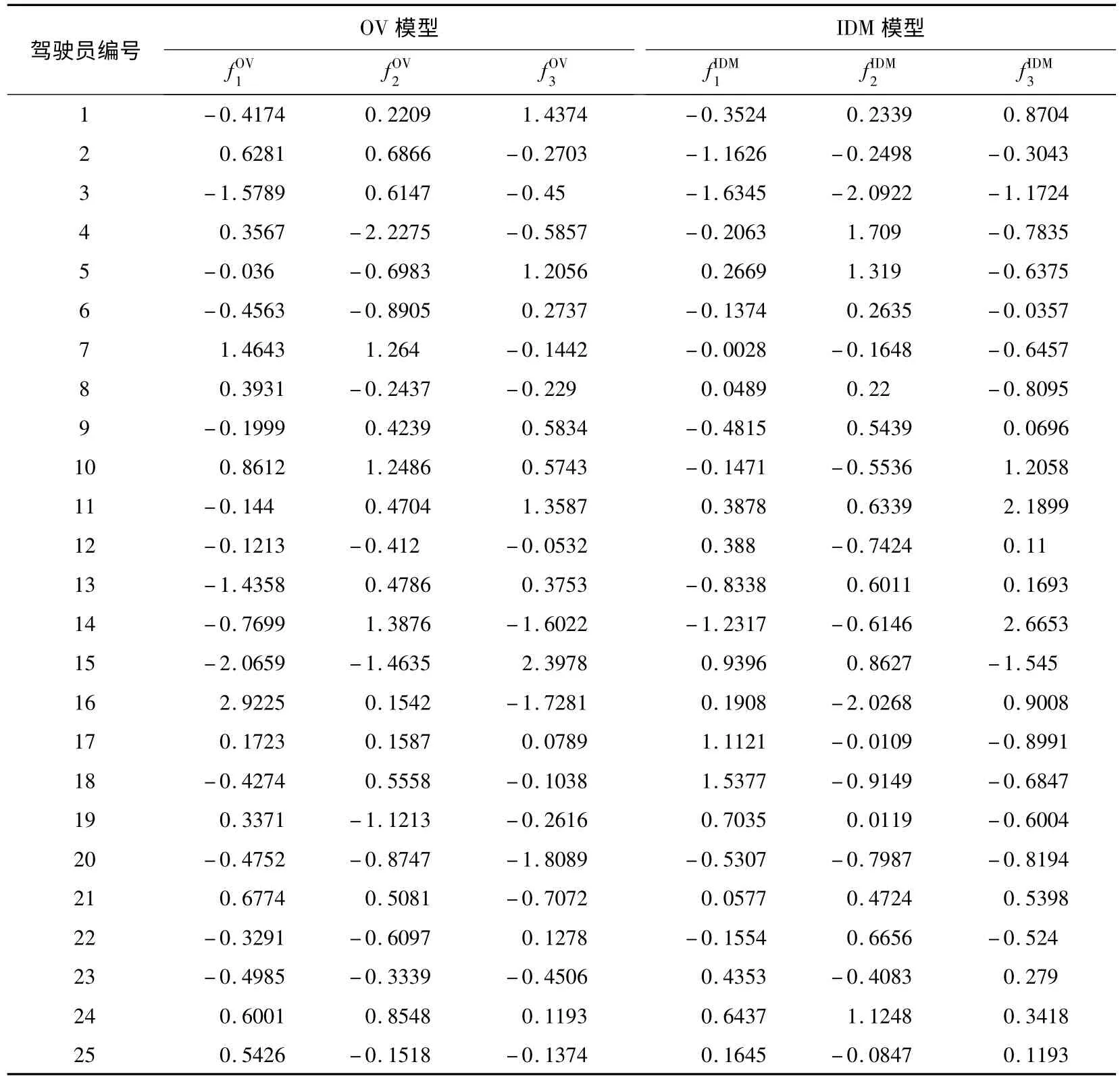
表1 OV 模型和IDM 模型中的特征因子取值Table 1 Characteristic factors in OV and IDM model

本文通过跟驰数据采集、数据处理和参数标定、参数相关性分析、特征因子计算、特征因子分布研究的步骤在跟驰数据基础上对车辆和驾驶员特性进行分类和深入分析。当样本的数据量较大时，可以根据特征因子的分布情况对样本中车辆和驾驶员的特性分布进行研究。当车辆和驾驶员的特性分布情况已知时，可以通过特征因子和模型参数之间的换算将车辆特性体现在交通仿真中。

3 各异性IDM 模型及数值模拟

3.1 参数离散方法

根据第2 节中提出的车辆和驾驶员特性分析方法，在车辆和驾驶员的特性分布形式已知时，可以通过特征因子与模型参数之间的换算将车辆特性体现在交通仿真中。本文中数据样本量较少，难以得出准确的车辆特性分布，因此在仿真中假设特征因子独立服从标准正态分布的形式。

以IDM 模型为例，将特征因子与参数变化方式联系起来，建立各异性跟驰模型。假设车辆的动态特征因子、静态特征因子和反应时间特征因子在仿真对象中服从相互独立的标准正态分布，则对于驾驶员i，模型各参数表达式为:

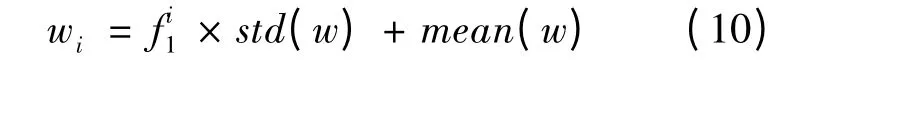
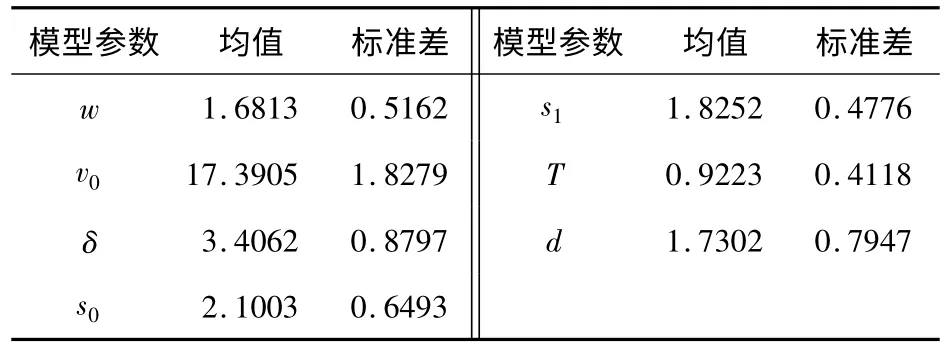
表2 IDM 模型参数的均值和标准差Table 2 Mean and standard deviation of parameters in IDM model

3.2 稠密交通流中扰动传播的数值模拟

对稠密交通流中扰动传播进行模拟，作如下假设:车队由35 辆车组成，起始车头间距为23 m，头车初速度为12.2 m/s。头车初始加速度为0，第6 ～7 s 加速度为－5.5 m/s2，第8 ～12 s 加速度为0，第13 ～14 s 加速度为4.25 m/s2，之后加速度恒为0，使得头车速度由12.2 m/s 减为1.2 m/s，持续4 s 并重新加速至9.7 m/s，形成一个向后传播的扰动。

采用各异性IDM 模型进行仿真，仿真开始时，每辆车的动态特征因子、静态特征因子和反应时间特征因子分别由独立服从标准正态分布的随机数生成，根据特征因子通过式(10)～(16)计算该驾驶员-车辆单元的模型参数。通过多次模拟研究特征因子取值及分布对交通流状态演变的影响，仿真结果如图3 所示。

经典IDM 模型是确定性模型，同种初始条件下的模拟结果总是一致的;在参数取值相同的情况下，车辆在跟驰过程中会表现出相同的特性，时间位移曲线的线型会趋于一致。从图中可看出，在各异性IDM 模型中，由于车辆和驾驶员的个体差异，其时间位移曲线呈现出不同的线型;随着特征因子的不同取值和车辆及驾驶员特性在交通流中分布方式的差异，扰动在稠密交通流中的传播会根据一定概率出现消散、稳定传播、增大等不同情况。仿真结果说明，各异性IDM 模型可以描述在车辆及驾驶员特性的影响下，交通系统可能出现的不同演化情形，与实际交通情况相符合。

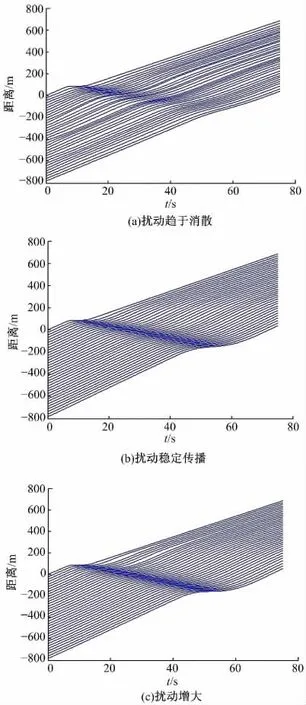
图3 车辆及驾驶员特性对稠密交通流中扰动传播的影响Fig.3 Influence of driver-vehicle characteristics on propagation of perturbations in dense traffic flow

4 结束语

提出了一种基于跟驰数据研究车辆和驾驶员特性的方法，方法步骤主要包括:跟驰数据采集-数据处理和参数标定-参数相关性分析-特征因子计算-特征因子分布研究。通过引入特征因子的概念，可以将车辆及驾驶员特性与模型参数取值有机联系起来，实现基于跟驰数据的车辆特性描述和分析，以及基于车辆和驾驶员特性的交通仿真，提高了交通仿真与实测数据的契合程度。

以OV 和IDM 模型为例实现了该车辆特性分析方法。在江苏省南京市进行跟驰数据采集，对OV 模型和IDM 模型进行参数标定。相关性分析表明:①不同模型的参数变化相关程度并不明显;②同一模型内的参数变化有较强的相关性。根据相关分析的结果将两种模型的参数分别分为3组，将每组高度相关的参数归纳为一个因子，计算出每个驾驶员-车辆单元的特征因子取值。由于本文采集的数据样本量较少，因此没有对车辆及驾驶员特性的分布形式进行深入研究。以IDM模型为例，假设车辆的3 个特征因子独立服从标准正态分布，实现了基于车辆和驾驶员特性分析的交通仿真。仿真结果表明，各异性IDM 模型可以描述在车辆特性的影响下交通系统可能出现的不同演化情形，与实际交通情况相符合。

［1］Newell G F.A simplified car-following theory:a lower order model［J］.Transportation Research Part B，2002，36(3):195-205.

［2］Ahn S，Cassidy M J，Laval J.Verification of a simplified car-following theory［J］.Transportation Research Part B，2004，38(5):431-440.

［3］贾洪飞，隽志才，王晓原，等.利用因子分析选取车辆跟驰模型输入变量［J］.公路交通科技，2004，21(1):81-84.Jia Hong-fei，Juan Zhi-cai，Wang Xiao-yuan，et al.Factor analysis for choosing input variables of car-following model［J］.Journal of Highway and Transportation Research and Development，2004，21(1):81-84.

［4］贾洪飞，隽志才，曹鹏.跟驰过程中驾驶员认知结构模型的建立［J］.公路交通科技，2005，22(11):130-132.Jia Hong-fei，Juan Zhi-cai，Cao Peng.A cognition structure model for drivers＇car-following behavior［J］.Journal of Highway and Transportation Research and Development，2005，22(11):130-132.

［5］王昊，王炜.各异性FVD 模型及数值模拟［J］.哈尔滨工业大学学报，2010，42(1):138-142.Wang Hao，Wang Wei.Heterogeneous FVD model and numerical simulation［J］.Journal of Harbin Institute of Technology，2010，42(1):138-142.

［6］敬明，邓卫，刘志明，等.基于车辆个体特征的IDM模型研究［J］.交通信息与安全，2012，30(5):10-13.Jing Ming，Deng Wei，Liu Zhi-ming，et al.IDM model based on individual features［J］.Journal of Transport Information and Safety，2012，30(5):10-13.

［7］敬明，邓卫.基于车辆个体行为的交通流跟驰模型研究［J］.交通科技，2008(6):84-87.Jing Ming，Deng Wei.Research on car following model that reflects individual differences［J］.Transportation Science＆Technology，2008(6):84-87.

［8］吴超仲，马晓风，严新平.考虑驾驶员反应能力的跟驰模型［J］.武汉理工大学学报:交通科学与工程版，2007，31(4):630-632.Wu Chao-zhong，Ma Xiao-feng，Yan Xin-ping.Car following model based on drivers'reaction time［J］.Journal of Wuhan University of Technology(Transportation Science＆Engineering)，2007，31(4):630-632.

［9］Bando M，Hasebe K，Nakayama A，et al.Dynamical model of traffic congestion and numerical simulation［J］.Physical Review E，1995，51(2):1035-1042.

［10］Treiber M，Hennecke A，Helbing D.Congested traffic states in empirical observations and microscopic simulation［J］.Physical Review E，2000，62(2):1805-1828.

［11］Wang Hao，Wang Wei，Chen Jun.General Newell model and related second-order expressions［J］.Transportation Research Record，2011，2260:42-49.

［12］Herman R，Montroll E W.Traffic dynamics:studies in car following［J］.Operations Research，1958，6(2):165-184.

［13］廖惠红，李丹，王昊，等.跟驰模型中反应延迟时间项作用机制的数值模拟［J］.交通信息与安全，2010，28(2):33-36.Liao Hui-hong，Li Dan，Wang Hao，et al.Numerical simulation of the perception/reaction delay time in carfollowing model［J］.Journal of Transport Information and Safety，2010，28(2):33-36.