利用坐标平移与坐标旋转方法的宏程序应用

2015-06-12李雅昔李晓莉李星恕

机械制造 2015年4期

□ 李雅昔 □ 李晓莉 □ 李星恕

1.商洛职业技术学院陕西商洛 726000

2.西北农林科技大学机电学院陕西杨凌 712100

3.长安大学信息工程学院西安 710064

机械加工中经常遇到非圆曲线（如椭圆曲线［1、2］、抛物线［3、4］、双曲线［5］和渐开线等）零件，随着产品性能要求的不断提高，非圆曲线零件的作用日益重要，其加工质量往往成为产品制造的关键。数控机床的数控系统一般只具有直线插补和圆弧插补功能，并不具备此类非圆曲线的插补功能，采用普通的手工编程方法几乎不可能完成这些轮廓的加工。若采用软件自动编程，生成的程序往往很复杂，且缺乏灵活性和通用性。通过宏程序编程可以实现普通编程难以实现的功能，且编写的程序具有极好的易读性、修改性和通用性。机床在执行宏程序时，相比执行CAM软件生成的程序更加快捷，反应更迅速。

本文以华中世纪星HNC-21T数控车削系统为例，借助坐标系平移［6、7］与坐标系旋转［8、9］的方法，对数控车床加工任意位置非圆曲线回转面的宏程序编写方法进行分析。

1 利用坐标平移与坐标旋转的方法在工件坐标系中建立非圆曲线方程

在实际加工中，工件坐标系原点常与待加工的非圆曲线方程所在坐标系原点不重合［10、11］，因此要找出两个坐标系之间的关系，以便于在工件坐标系中重新建立非圆曲线方程。由于数控车床的轮廓设在XOZ平面上，给定非圆曲线方程所在坐标系中任意一点的坐标通过坐标平移与坐标旋转的方法，可以在工件坐标系中得到相应的新坐标。而数控车床没有坐标平移与坐标旋转指令，所以必须对不同坐标系中的非圆曲线方程进行相应的数学处理。

1.1 坐标平移法

当待加工非圆曲线给定方程的坐标系X1O1Z1与数控车床工件坐标系XOZ仅存在平移关系时，可通过坐标平移的方法建立这两个坐标系之间的关系。如图1所示，工件坐标系为XOZ，待加工非圆曲线给定方程的坐标系为X1O1Z1。假定A点在X1O1Z1坐标系中的坐标为（x1，z1）,工件坐标系XOZ的原点O在坐标系X1O1Z1中的坐标为（i，k），通过式（1）建立两坐标系之间的关系，可将X1O1Z1坐标系中的A点坐标（x1，z1）转换为数控车床工件坐标系 XOZ 中 A点坐标（x，z）。

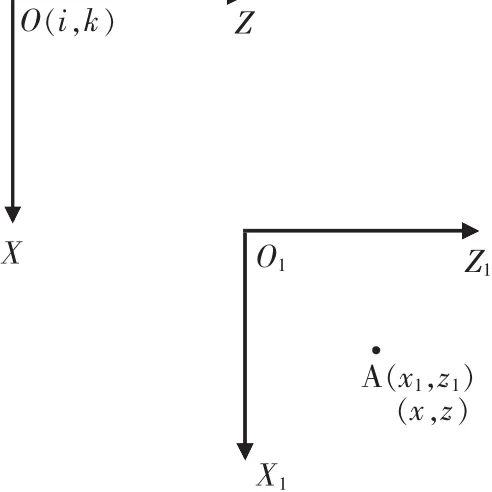
▲图1 坐标系平移

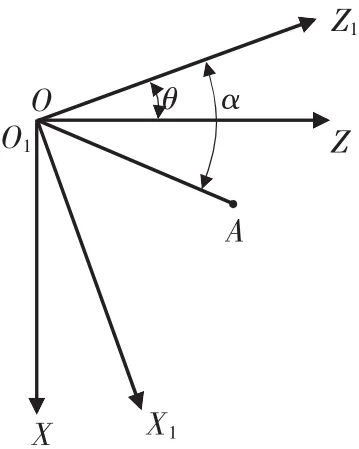
▲图2 坐标系旋转

▲图3 坐标系平移与旋转

1.2 坐标旋转法

当待加工非圆曲线给定方程的坐标系X1O1Z1与数控车床工件坐标系XOZ仅存在旋转关系时（即两坐标系坐标原点重合），可通过三角函数关系建立这两个坐标系之间的关系。如图2所示，假定A点在原坐标系 X1O1Z1中的坐标为（x1，z1）,线段 OA 与 Z1轴的夹角为 α，则：

当原坐标系X1O1Z1绕坐标原点O1顺时针方向旋转角度θ后与工件坐标系XOZ重合时，点A在工件坐标系XOZ中的坐标为（x，z）。OA与Z轴的夹角为（αθ），可得：

由三角函数的运算法则可得A点在工件坐标系XOZ中的坐标值为：

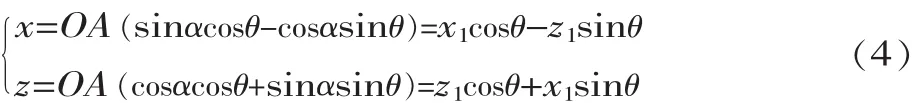
当原坐标系X1O1Z1绕坐标原点O逆时针方向旋转角度θ后与工件坐标系XOZ重合时，A点在工件坐标系XOZ中的坐标值为：

1.3 同时使用坐标平移法与坐标旋转法

当待加工非圆曲线给定方程的坐标系X1O1Z1与数控车床工件坐标系XOZ既存在坐标系平移又存在坐标系旋转时，可先按坐标系旋转进行分析，再按坐标系平移进行分析，建立这两个坐标系之间的关系。如图3所示，坐标系X2O2Z2与坐标系X1O1Z1仅存在旋转关系，同时坐标系X2O2Z2与工件坐标系XOZ仅存在平移关系，且工件坐标系原点O在坐标系X2O2Z2中的坐标为（i，k）。假定 A 点在 X1O1Z1中的坐标为（x1，z1）, 由式（4）、（5）可得出 A 点在坐标系 X2O2Z2中的坐标（x1cosθ∓z1sinθ，z1cosθ±x1sinθ） , 由式（1）可得 A 点在工件坐标系XOZ的坐标值：

式（6）中正负号的规定与式（4）、式（5）中正负号的规定相同。

2 车削非圆曲线轮廓宏程序编程思路

2.1 宏程序简介

使用变量编写可进行算术或逻辑运算，并能控制程序段流向的程序，称为用户宏程序。华中世纪星HNC-21T数控车削系统为用户配备了类似于高级语言的宏程序功能，用户可以使用变量进行算术运算、逻辑运算和函数的混合运算，此外宏程序还提供了循环语句、分支语句和子程序调用语句，利于编制各种复杂的零件加工程序，减少乃至免除手工编程时进行繁琐的数值计算，精简程序量。常用的语句主要有以下两种。

（1）条件判别语句。

格式1：IF（条件表达式）… ELSE… ENDIF

格式2：IF（条件表达式）… ENDIF

（2）循环语句。

格式：WHILE（条件表达式）…ENDW

2.2 公式表达非圆曲线宏程序编制的一般步骤

（1）在工件坐标系XOZ中建立待加工非圆曲线的表达式，选定自变量并确定自变量的取值范围。根据给定的非圆曲线方程进行坐标系平移或坐标系旋转，将待加工非圆曲线方程转变为工件坐标系XOZ中新的表达式。选择合适的自变量来表示曲线上各关键点的坐标表达式，这一点在宏程序的编写过程中尤为重要。自变量的选择一般根据曲线方程方便情况来选定，自变量选定后，还需进一步确定其取值范围。

（2）选择拟合方式并确定自变量的步距。选择拟合方式，即选择采用直线段还是圆弧段来拟合非圆曲线。在确定自变量的步距时，一般根据所用机床的性能和工艺装备，确定自变量的步距。步距取值越小，轮廓表面的拟合误差越小，加工精度越高，但加工效率很低。步距取值越大，轮廓表面的拟合误差越大，加工精度越低，但加工效率很高。一般情况下，自变量的步距取 0.05～0.2 mm。

（3）自变量的赋值与加工的终点判别。给定自变量的初值与终值，机床每移动一个步距后，自变量递变，根据加工终值判别条件，与加工终值进行判别，当条件不满足（即未加工到非圆曲线终点）时，执行新的步距，继续循环加工，当条件满足（即加工到非圆曲线终点）时，完成非圆曲线轮廓的加工，退出循环。非圆曲线轮廓数控加工流程图如图4所示。

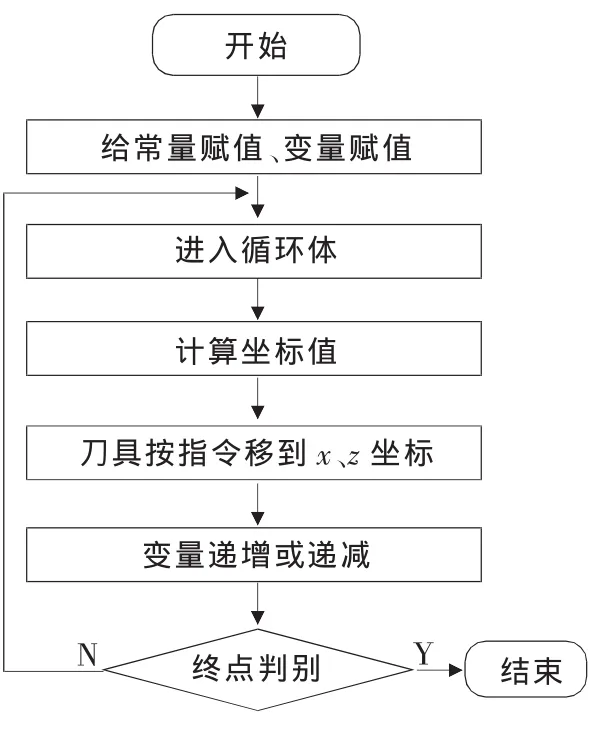
▲图4 椭圆轮廓数控加工流程图

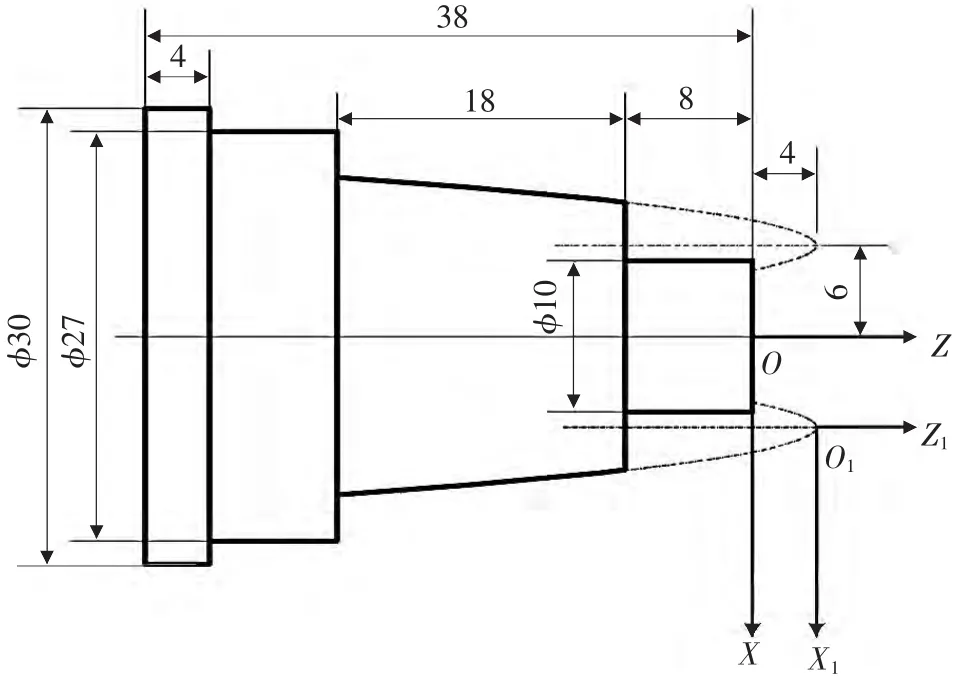
▲图5 平移关系的零件加工图

▲图6 数控仿真结果

（4）编写程序。因为一般毛坯存在较大的加工余量，故一般需采用粗车循环指令［12］与宏程序嵌套［13、14］的方法编写程序。

3 非圆曲线轮廓宏程序编写实例

3.1 仅存在平移关系时的宏程序编写方法

零件加工图如图5所示，工件坐标系XOZ的原点为φ10 mm圆柱右端面中心，与给定抛物线方程的坐标系X1O1Z1的原点不重合，工件坐标系原点O在原坐标系 X1O1Z1中的坐标为（-6，-4），根据式（1），可以得出此时在工件坐标系XOZ中抛物线表达式为：z-4=-1.5（x-6）2，因 z的取值范围容易确定，故取 z为自变量，在工件坐标系XOZ中，建立待抛物线方程：x=6+，其中自变量z的初值为-8，终值为-26。

根据上述数学分析，编写待加工非圆曲线的宏程序，其子程序如下：

%0003

#5=-1.5 //抛物线方程系数赋值

#6=-8 //自变量z的初始值赋值

#7=-26 //自变量z的终止值赋值

WHILE#6 GE#7//建立循环条件：判断自变量z是否达到加工终值-26

#8=6+SQRT［［#6-4］/#5］ //给因变量 x 赋值，即

G01 X［2*［#8］］ Z［#6］ F0.2//小段直线插补，逼近抛物线轮廓

#6=#11-0.05 //z步进为0.05，自变量递减

ENDW

M99

数控仿真加工结果如图6所示。