基于三次B样条曲线的食品物性检测系统的仿生咀嚼运动轨迹规划
2015-06-12马德军王加森俞经虎
□ 马德军 □ 王加森 □ 卢 慧 □ 俞经虎,2
1.江南大学 机械工程学院 江苏无锡 214122
2.江苏省食品先进制造装备技术重点实验室 江苏无锡 214122
随着食品行业的工业化和标准化发展,目前,市场已有的食品物性检测质构仪[1]多为功能单一的专用仪器,而且测试运动也为简单的上下直线运动,而物性检测的最终标准是人的口腔咀嚼感觉,本文研究的基于6-UPS并联机器人[2]食品物性检测装置,通过模仿人的咀嚼运动来实现对食品物性参数的检测,从原理上有助于提高食品物性的检测准确性 。
以仿生学为基础,根据正常人下颌咀嚼运动的运动轨迹扫描研究的结果,对仿生咀嚼运动空间轨迹进行构建,然后利用运动学逆解将笛卡尔空间运动轨迹转换为连杆空间运动,最终利用三次B样条函数在连杆空间路径点之间进行插值运算,构造出仿生咀嚼运动的连杆运动轨迹函数,并运用实例验证轨迹规划效果。
1 6-UPS并联机器人结构参数设置及坐标建立
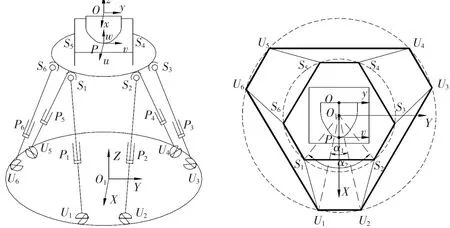
▲图1 6-UPS并联机构的结构简图及俯视图
6-UPS并联机构初始位置时的结构简图及俯视图如图1所示,上平台和下平台的中心点在水平投影面上相重合。图中标注了下平台的下铰点Ui(i=1,2,...,6),Ui绕圆周依次排列形成不等边对称六边形,其中U1U3U5、U2U4U6分别形成等边三角形,外接在半径为R的圆上,短边U1U2所对应的圆心角为α1;上平台上铰点在图中表示为 Si(i=1,2,...,6),Si也形成一个不等边对称六边形,其中S1S3S5、S2S4S6分别构成等边三角形,z外接在半径为r的圆上,长边S1S2所对应的圆心角为α2。
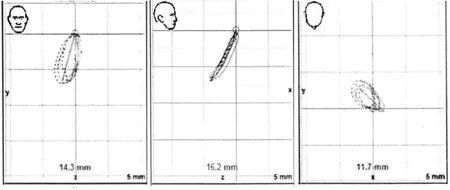
▲图2 26~30岁的正常人群咀嚼运动轨迹在冠状面、矢状面和水平面的投影
为了便于分析与计算,建立如图1所示坐标系。在并联机构下平台上建立全局坐标系O1-XYZ,坐标原点O1是下平台的几何中心点,轴线X垂直于短边U1U2,轴线Z经过上下平台的几何中心点向上,轴线X、Y、Z方向满足右手定则;建立静坐标系O-xyz,固结于上颌骨,静坐标系原点O是左右髁突铰链轴的中心点,轴线 x、y、z与全局坐标系{O1}的 X、Y、Z 平行;动坐标系P-uvw固结于下颌骨上,坐标原点P为下颌切点,轴线u、v、w方向满足右手定则,如图1所示,初始位置与全局坐标系的X、Y、Z平行。
2 仿生咀嚼运动空间轨迹构建
昆明医科大学的李娟[3]采用SAM下颌运动轨迹扫描记录仪检测了不同年龄组正常人群咀嚼运动的轨迹及幅度,根据正常人群咀嚼运动轨迹的测试结果,绘出了26~30岁的人群冠状面、矢状面和水平面的咀嚼运动轨迹的咀嚼运动图,如图2所示。
从图2的总体看,人的咀嚼运动轨迹是复杂的,但从单张图可以发现,在冠状面中咀嚼运动轨迹近似为一个倾斜的椭圆,而反映人在咀嚼运动时,张口和闭口的运动轨迹在矢状面内的轨迹基本相重合,咀嚼运动轨迹在水平面内的扫描轨迹也近似于一个倾斜的椭圆。根据以上分析结果,可以认为正常人咀嚼运动的笛卡尔空间轨迹形状与空间椭圆相近似。为了实现基于6-UPS并联机器人的食品物性仿生检测平台良好的运动仿生特性,决定将咀嚼运动的轨迹等效为空间椭圆轨迹,该空间椭圆轨迹可以由平面椭圆通过几个空间的位姿变换最终确定,椭圆上的点(即动坐标系原点)在静坐标系中的位置为:式 中 :sφT为 sinφT;cφT为cosφT;a、b 分别为椭圆轨迹的长半轴和短半轴;φT、θT分别为椭圆长轴在与初始动坐标系位姿相同的固定坐标系的xoz平面和yoz平面内的投影与z轴负方向的夹角;α11为椭圆运动角度;h为上下平台间的垂直距离;h1为动坐标系原点P距上平台的垂直距离;h2为静坐标系原点O距下平台的垂直距离。
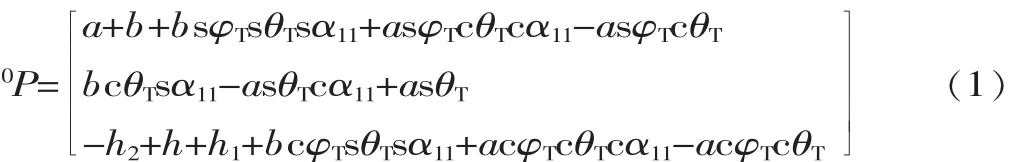
以上为动坐标系原点P在α11处的位置,要求出动坐标系原点P在静坐标系{O}中的位姿还需要求动坐标系在α11处的姿态变化。
根据咀嚼运动的实际情况可知,人的下颌骨在运动的过程中,姿态的变化可分解为绕静坐标系的y轴旋转的张口运动和绕静坐标系的z轴旋转的左右摆动。当动坐标系原点运动到某一位置时,这两个角度可由动坐标系原点P与静坐标系原点O的连线的向量OP分别在xoz和xoy平面上与x轴正方向的夹角表示。
设向量OP在xoz平面上与x轴正方向的夹角为φ1,即动坐标系绕静坐标系的y轴旋转角度。向量OP在xoy平面上与x轴正方向的夹角为φ2,即动坐标系绕静坐标系的z轴的旋转角度。由下式可求得:
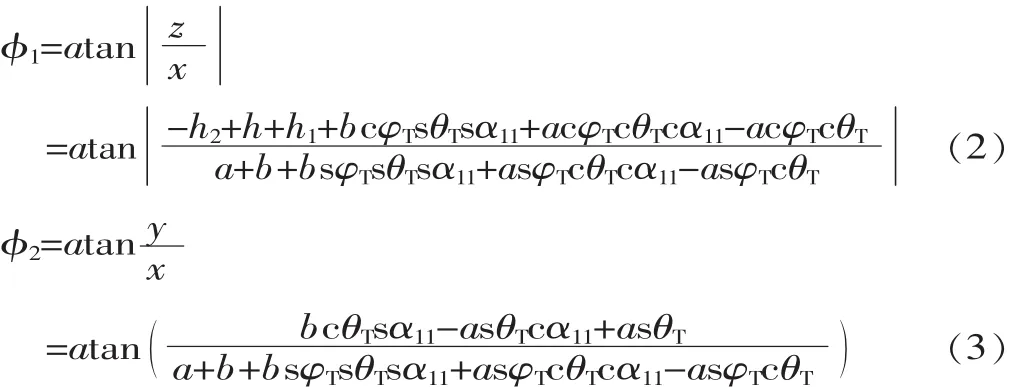
至此,在空间运动轨迹中某一时刻,动坐标系的位姿参数全部确定。
3 基于三次B样条的仿生咀嚼运动连杆空间轨迹规划
连杆空间用三次B样条曲线进行轨迹规划就是通过B样条函数的反算方法得到各连杆变量l关于时间t的函数表达式[4],反算就是利用给定的B样条曲线上的部分已知路径点,来求解B样条曲线的控制点(特征多边形顶点),进而构造曲线的函数表达式。
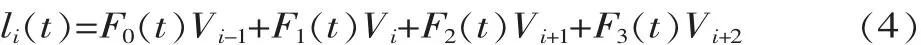
设某段时间内三次B样条曲线的函数式为:式中:t为时间(0≤t≤1);F(t)为时间变量的多项式,即三次 B 样条的基函数; Vi-1、Vi、Vi+1、Vi+2为该段三次B样条曲线的控制点。
根据连杆轨迹的连续性、连杆轨迹导数的连续性、B样条基函数的规范性条件推导可得:
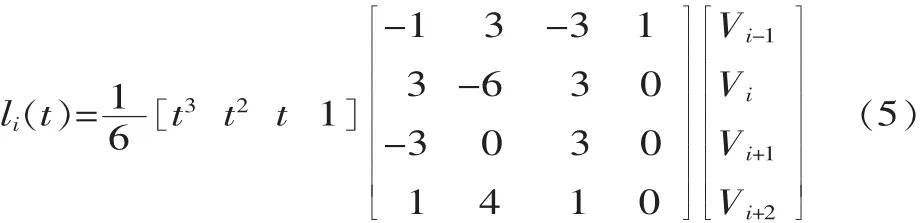
由式(5)可知,要计算B样条函数的表达式首先需要求出一系列控制点Vi。由于假设并联机器人各连杆路径点为已知,所以不妨假设某连杆的轨迹有m-1段三次 B 样条曲线组成,路径点为 pi(i=1,2,...,m),由轨迹连续性可得:
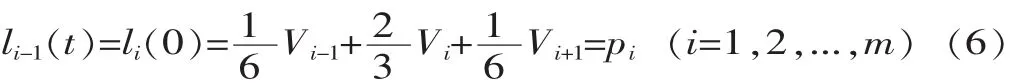
根据模拟咀嚼运动的实际情况,各连杆运动轨迹在初始点和终止点的速度需为零,以此作为边界约束条件[5],可得:
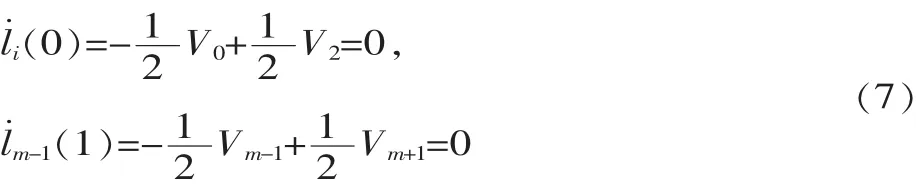
将式(6)和式(7)联立写成矩阵形式为:
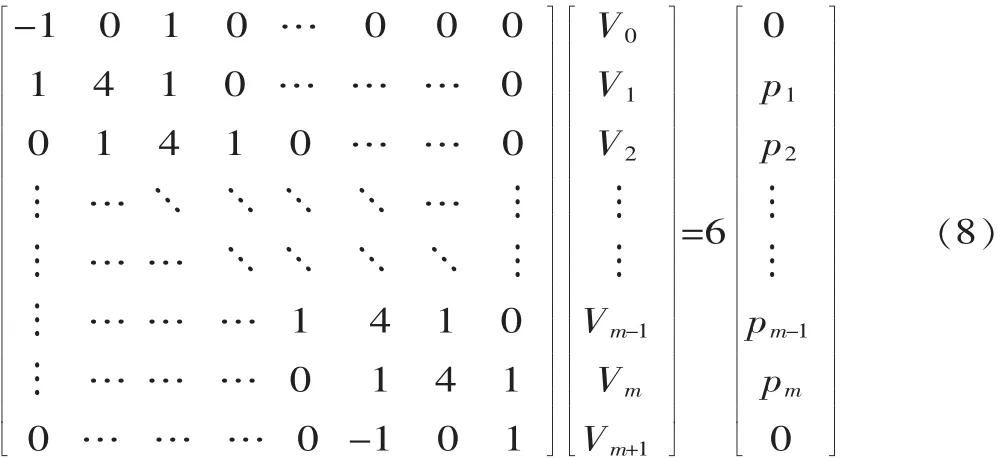
由式(8)可以看出,该线性方程组共有m+2个未知数,同时有m+2个方程,故可以确定唯一解V0、V1、...、Vm、Vm+1。
这样,根据已知路径点即可得到B样条曲线的所有控制点,机器人各连杆的整个运动轨迹可由m-1个三次B样条函数分段表示,进而可得到整个连杆轨迹的表达式。
4 仿生咀嚼运动轨迹规划实例
根据设计的仿生咀嚼平台的尺寸及作咀嚼运动的轨迹运动范围的大小,分别取各参数如下。
初始位置时,取上下平台间的垂直距离h=200 mm,上平台外接圆半径r=50 mm,下平台外接圆半径R=100 mm,动坐标系原点P距上平台的垂直距离h1=50 mm,距全局坐标系原点O1的水平正向距离a1=50 mm,静坐标系原点O距下平台的垂直距离h2=(h+h1+20)mm,距全局坐标系原点O1的水平负向距离b1=50 mm。
而对于空间椭圆轨迹,取椭圆的长半轴a=50 mm,短半轴 b=30 mm,φT=atan(1/2),θT=π/12。 设动坐标系沿椭圆轨迹运动一周所用的周期T1=4 s,则运动的角速度ω=π/2(rad/s)。轨迹规划时将椭圆轨迹均等分成n=8份,则对应节点的椭圆运动角度α11=ωt,其中t为对应节点的时刻。此外,上平台铰点构成的六边形的长边所对应的外接圆圆心角α2=5π/12,下平台铰点构成的六边形的短边所对应的外接圆圆心角α1=π/4。将椭圆运动轨迹等分成n=8份,根据参量的设置,即α11=(π/4)i(i=0,1,...,8)。
由动坐标系的位置时间式(1)及动坐标系姿态时间式(2)和式(3),将参数值代入后,可分别求出9个节点处动坐标系在静坐标系的位置和姿态。将求得的笛卡尔空间椭圆轨迹上的9个节点处动坐标系在静坐标系的位置和姿态值代入逆运动学推导获得的公式,即可求出时刻上铰点 Si(i=1,2,...,6)在坐标系{O}中的坐标值和对应节点处连杆的杆长。
至此,完成了由笛卡尔空间椭圆轨迹上的点到连杆坐标系杆长的求解。根据以上参数求解的节点杆长结果,代入三次B样条曲线控制节点求解式(8),求得三次B样条曲线的控制节点V的结果。


以上方程为三次B样条曲线的求解公式,推导出6根连杆的三次B样条曲线插值方程。
综上可以看出,将椭圆轨迹按周期等分成8段,由根据路径点求解出构建3次B样条曲线函数所需要的10个控制节点对每段进行插值,最终可以看到机器人各连杆的整个运动轨迹可由8个三次B样条函数分段表示,进而可得到整个连杆轨迹的表达式。
对应以上获得的6根连杆三次B样条曲线轨迹规划方程,轨迹的杆长l、速度v、加速度a变化曲线分别如图3所示。
从轨迹规划方程的杆长变化曲线图和速度变化曲线图可以看出,6根连杆的杆长变化和伸缩速度变化平滑且连续,而且轨迹规划获得的方程能够很好地满足初速度和结束速度为零的要求。说明上述利用三次B样条曲线进行连杆轨迹规划的推导过程完全合理正确。
5 结束语
笔者以实现食品物性检测系统检测运动的仿生咀嚼运动为目标,通过对人下颌咀嚼运动轨迹进行分析,建立了检测运动的空间仿生咀嚼运动轨迹,运用运动学反解和三次B样条曲线,构建出了便于实现控制的连杆运动轨迹方程,为食品物性检测系统的研究提供了良好的理论基础和设计思路。
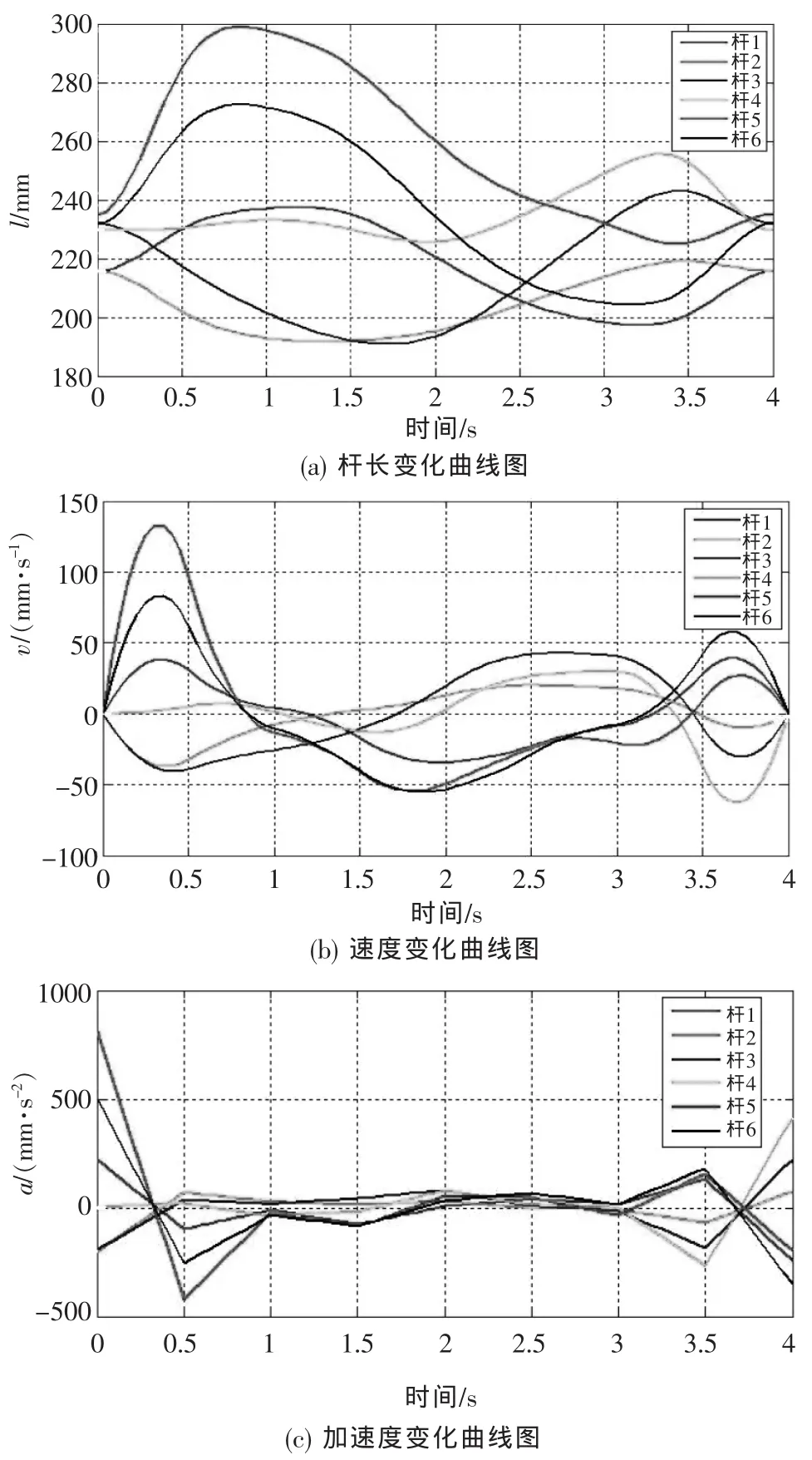
▲图3 6根连杆轨迹规划方程的杆长、速度、加速度变化曲线图
[1] 胡亚云.质构仪在食品研究中的应用现状[J].食品研究与开发,2013,34(11):101-104.
[2] 吴培栋.Stewart平台的运动学与逆动力学的基础研究[D].武汉:华中科技大学,2008.
[3] 李娟.不同年龄组正常人群的下颌运动轨迹及咀嚼肌表面肌电比较研究[D].昆明:昆明医科大学,2013.
[4] 牛永康.六自由度串联机器人轨迹规划时间最优研究[D].长春:长春工业大学,2013.
[5] 张洪强.工业机器人时间最优轨迹规划[D].长沙:湖南大学,2004.
