多尺度变换近邻传播算法

唐 敏

（1.安徽矿业职业技术学院 自动化与信息工程系，安徽 淮北 235000；2.淮北煤电技师学院 自动化与信息工程系，安徽 淮北 235000）

0 引 言

近邻传播算法是Frey和Dueck2007年在《Science》上提出的基于所有数据点相似度的新型聚类算法，目前该算法已经成功应用在图像分割［1－2］、视频拷贝检测［3］、文本聚类［4－5］确定等诸多领域，引起国内外学者的广泛关注，例如加拿大学者Inmar E.Givoni［6］等2009年提出一个派生的近邻传播算法，比原来更简单的基于一个完全不同的图形化模型；韩国学者Qasim I［7］等2013年提出吸引子传播算法与文本概念图半自动生成技术相结合，获得概念图领域专家的认可；国内学者肖宇［8］等提出一种适用于近邻传播算法的半监督方法，取得了显著成效；董俊［9］等提出可变相似度用于改进输入矩阵等。在研究以上算法基础上，提出一种基于多尺度变换的近邻传播算法，该算法更适合对高维数据聚类。

1 吸引子传播聚类算法

近邻传播算法不同于K均值，K均值对于初始聚类点的选择敏感，捕捉到聚类质量高的结果需要进行多次不同的初始化聚类参数，而近邻传播算法采用一种将所有数据点作为潜在聚类中心的新方法，该算法核心思想是信息传播过程中每个数据点都会找到自己归属的类［10］。近邻传播算法的输入值是数据点之间的相似性矩阵，见式（1），其中S（k，k）更容易成为聚类中心［11］。而最终聚类效果受偏向参数P值影响很大，P值一般选取输入相似度矩阵的中值，会产生一个适中的类数或者最小的类数［12］。数据点之间存在着两种信息交换，见式（2）和式（3），每个数据点都会参与两种类别信息的竞争，这两种信息会决定在任意时间数据点的归属情况，吸引度矩阵R是数据点i发送到候选类中心k的信息，决定k作为数据点i聚类中心的适合程度［13］。归属度矩阵A是候选类中心k发送给数据点i的信息，决定数据点i选择k做为类中心的适合程度［14］，当更多数据点和候选聚类中心k吸引度是正数时，k作为类中心的可能性会增大。为了限制吸引度这种巨大影响，归属度的迭代公式会不一样，是为避免它们之间的和为0。式（4）用来决定谁是真正的聚类中心，当聚类中心点重合，或者达到最大迭代次数，信息传递过程就会结束［15］。同时，该算法为了避免震荡性不断增大，使用式（5）和式（6）解决这个问题，不断更新吸引度矩阵和归属度矩阵，一般取λ＝0.5，聚类中心连续10次没有变化时，算法结束［16］。

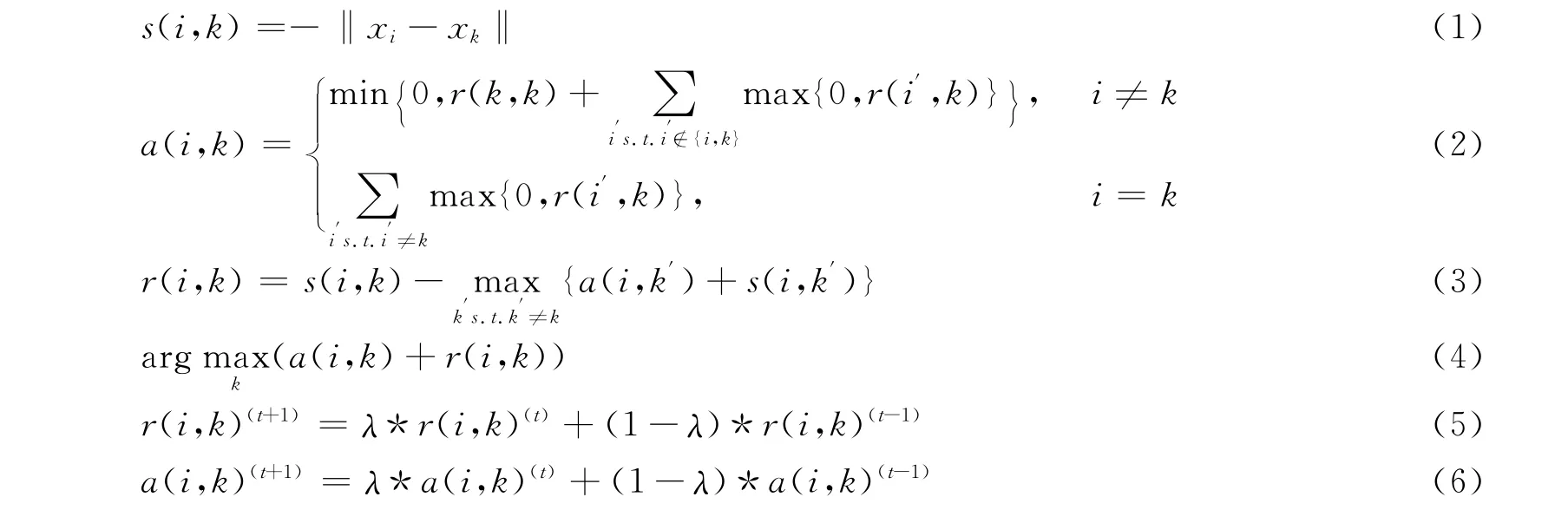
2 多尺度变换

MDS是基于数据点之间的相似性或者距离，并在低维空间表示出来［17］。基本原理就是约简后低维空间任意两点间的距离应该与它们在原高维空间中的距离相同［18］，MDS的求解过程用式（7）～式（9）等合适的准则函数来体现在低维空间中对高维聚类的重建误差，可以通过梯度下降法对这些函数求解。

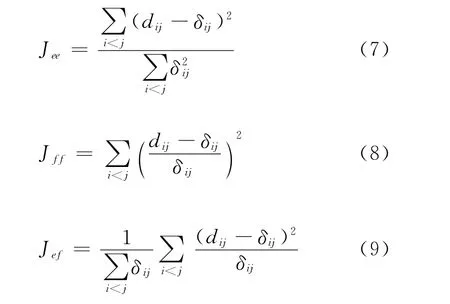
MDS是一种非监督的降维方法，文中选用Matlab软件自动生成三维二项分布数据，如图1和图2所示。

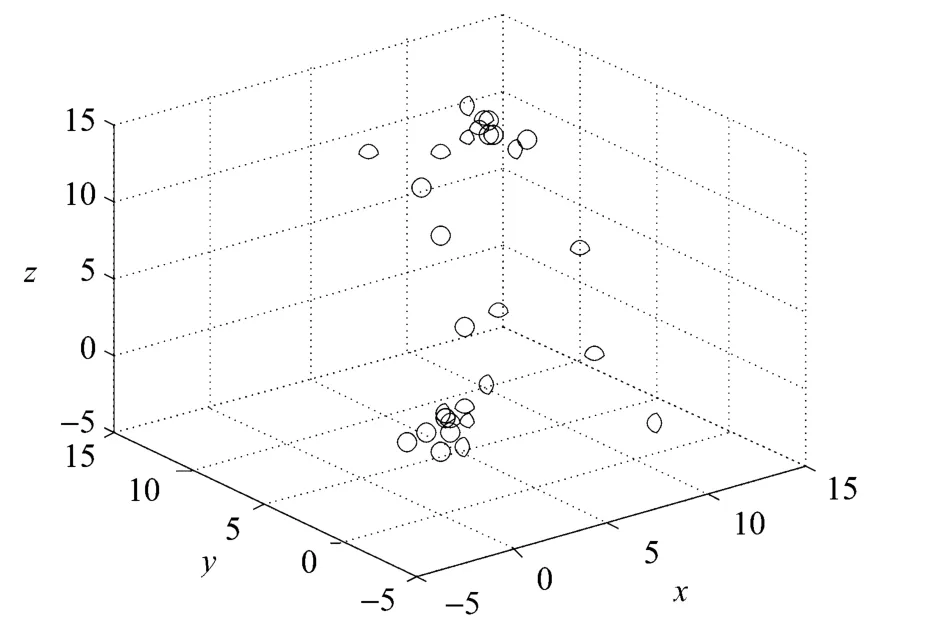
图1 二项分布数据三维视图

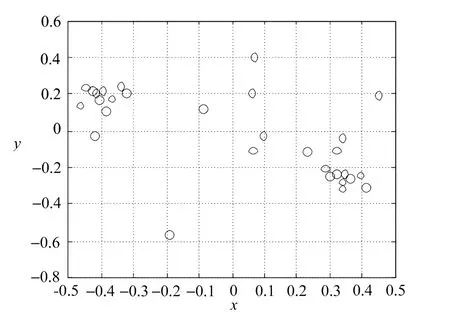
图2 MDS后二项分布数据视图

图1是该数据的空间分布，经过MDS映射到二维空间，图2是该数据的平面映射分布。从视觉上看，两种数据分布情况空间距离感是一致的，数据点间的距离保持不变。

3 基于多尺度变换的近邻传播算法MDSAP

近邻传播算法对于高维数据的处理性能不佳，维度增高，算法收敛速度变慢，甚至无法收敛。聚类精度也越来越低，因此，文中采用MDS降维方法，从图1和图2可以看到数据点间的空间距离没有变化，也就是说，原本是一类的数据还是归属到一类中，这符合聚类假设的原理，利用MDS降维后对于数据点归属和产生的类的个数没有影响。

基于稳定阈值的吸引子传播聚类算法如下：

1）输入相似性矩阵S（i，j）；

2）设置输入矩阵，MDS运算；

3）设置搜索偏向参数，初始偏向参数是相似性矩阵S（i，j）的中位数；

4）更新矩阵R和矩阵A；

5）更新吸引度和归属度矩阵；

6）达到最大迭代次数，算法结束。

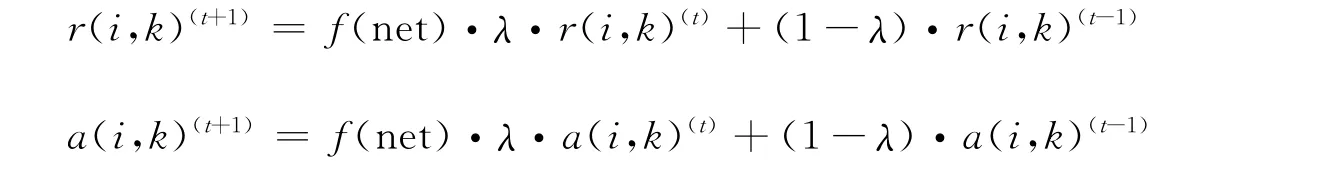
4 仿真模拟实验

仿真模拟实验环境为Pentium G645 2.9GHz CPU，4GB内存。所有编程都在Matlab R2012b上完成和仿真。实验数据集参数及AP和MDSAP聚类算法实验结果比较分别见表1和表2。

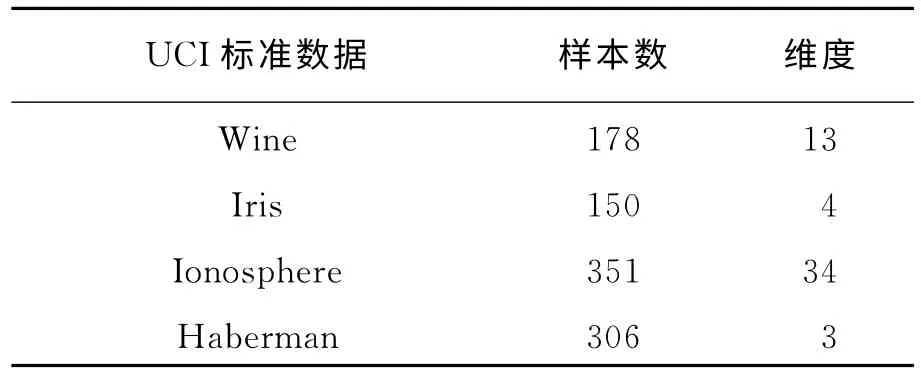
表1 实验数据集参数

表2 AP和MDSAP聚类算法实验结果比较

实验所采用的数据集都是UCI标准数据集，保持数据的真实性和有效性，为验证该算法的聚类效果，选用同种实验数据，并采用Silhouette指标作为约束规则的考量标准，该指标利用类内平均距离和最小类间距离评价聚类结果，Sil值大于0.5，说明聚类空间界限分明，Sil值小于0.5，说明聚类空间出现重叠，而Sil小于0.2代表聚类结果失真［19］，通过此指标来衡量改进后算法的好坏，而对于聚类结果有重大影响的偏向参数P值，都采用相似性矩阵的中值，不做任何改变。以上控制了影响算法结果的所有外在参数，保证对比试验得出的结论是科学有效的。

表1选用2个低维数据集Iris和Haberman，2个高维数据集Wine和Ionosphere，方便观察MDSAP在低维和高维的表现，表2是AP和MDSAP实验结果对比，可以看出，低维数据集Iris和Haberman差距较小，MDSAP精度值只有较小幅度提高，而Wine数据集维度是13，稍高于其它数据集，精度差距只有0.8左右。对于34维的Ionosphere数据集，可以很清楚地看到改进的MDSAP聚类算法的优越性，面对高维数据，能够较好地改良传统算法的收敛性和增加聚类精度。以上结果说明，基于多尺度变换的近邻传播算法聚类性能是高于原算法的，而且维度越高，MDSAP聚类算法的优越性越大。

5 结 语

近邻传播聚类算法作为一种无须事先指定类数的算法广受关注，文中针对该算法面向高维数据聚类效果不好的弊端，利用多尺度变换能够将高维数据映射到低维空间的特点，将二者结合，增强近邻传播算法在高维数据挖掘领域的应用能力。经过标准数据集的比较测试得出，文中提出的基于多尺度的近邻传播算法比传统算法精度更高，聚类效果更好。

［1］ 许晓丽，卢志茂，张格森，等.改进近邻传播聚类的彩色图像分割［J］.计算机辅助设计与图形学学报，2012，24（4）：514－519.

［2］ 施成湘.基于二次分水岭和近邻传播聚类的彩色图像分割算法研究与实现［J］.西南师范大学学报：自然科学版，2013，38（8）：125－129.

［3］ 许喆，薛智锋，陈福才，等.基于改进的近邻传播学习算法的视频拷贝检测［J］.计算机工程与设计，2014，35（9）：3185－3189.

［4］ 文翰，肖南峰.基于强类别特征近邻传播的半监督文本聚类［J］.模式识别与人工智能，2014（7）：646－654.

［5］ 卢志茂，李纯，张琦，等.近邻传播的文本聚类集成谱算法［J］.哈尔滨工程大学学报，2012，33（7）：899－905.

［6］ Inmar E Givoni，Frey B J.A binary variable model for affinity propagation［J］.Neural Computation，2009，21（6）：1589－1600.

［7］ Qasim I，Jeong J W，Heu J U，et al.Concept map construction from text documents using affinity propagation［J］.Journal of Information Science，2013（11）：1281－1290.

［8］ 肖宇，于剑.基于近邻传播算法的半监督聚类［J］.软件学报，2008，19（11）：2803－2813.

［9］ 董俊，王锁萍，熊范纶，等.可变相似性度量的近邻传播聚类［J］.电子与信息学报，2010，32（3）：509－514.

［10］ 鲁伟明，杜晨阳，魏宝刚，等.基于MapReduce的分布式近邻传播聚类算法［J］.计算机研究与发展，2012，49（8）：1762－1772.

［11］ 王娟，王萍.直接零件标志条码区域定位算法［J］.计算机辅助设计与图形学学报，2014，26（7）：1159－1166.

［12］ Dueck D，Frey B J.Non－metric affinity propagation for unsupervised image categorization［C］／／Computer Vision，2007.［S.l.］：IEEE 11th International Conference on IEEE，2007：1－8.

［13］ Lu Z，Carreira－Perpinan M A.Constrained spectral clustering through affinity propagation［C］／／Computer Vision and Pattern Recognition，2008.［S.l.］：Conference on IEEE，2008：1－8.

［14］ 杜锡寿，陈庶樵，张建辉，等.P2P流量的精细化识别方法研 究［J］.电 子 与 信 息 学 报，2012，34（7）：1709－1714.

［15］ 冷亚军，梁昌勇，陆文星，等.基于改进近邻传播算法的Web用户聚类［J］.情报学报，2012，31（9）：993－997.

［16］ Leone M，Weigt M.Clustering by soft－constraint affinity propagation：applications to gene－expression data［J］.Bioinformatics，2007，23（20）：2708－2715.

［17］ 何光辉，张太平，唐远炎，等.非监督子空间学习中关联度量多维尺度分析［J］.中国图象图形学报，2011，16（12）：2152－2158.

［18］ 孙键，赵红，赵宇彤，等.基于多维尺度分析的企业社会责任重叠测评实证研究［J］.数学的实践与认识，2011，41（9）：106－114.

［19］ 刘晓楠，尹美娟，李明涛，等.面向大规模数据的分层近邻传播聚类算法［J］.计算机科学，2014，41（3）：185－188，192.