财政科技投入周期与经济周期协同性的马尔科夫区制转移模型
2015-06-12潘方卉李翠霞
潘方卉,李翠霞,樊 斌
(东北农业大学经济管理学院,黑龙江 哈尔滨 150030)
财政科技投入周期与经济周期协同性的马尔科夫区制转移模型
潘方卉,李翠霞,樊 斌
(东北农业大学经济管理学院,黑龙江 哈尔滨 150030)
基于三阶段马尔科夫区制转移模型,对改革开放以来的财政科技投入周期和经济周期的动态过程进行阶段性变迁识别与协同性分析。研究发现:财政科技投入周期与GDP周期中存在着低速增长、适度增长和高速增长三种区制,并以一定的概率水平相互转化;财政科技投入处于低速增长和高速增长阶段的持续性与波动性强于同一阶段上的GDP,而处于适速增长阶段的持续性和波动性则弱于该阶段上的GDP;20世纪90年代初是财政科技投入周期与GDP周期同步与否的分水岭。在此之前,财政科技投入周期与GDP周期是非协同的,在此之后,先表现出静态协同关系,后呈现出动态协同关系,但是与财政科技投入周期相比,宏观经济周期具有一定的时间滞后性。
财政科技投入周期;经济周期;协同性;马尔科夫区制转移模型
1 引言
无论是在理论上还是实践上,财政科技投入与经济增长之间密切相关均已得到了广泛认可,有代表性的研究成果有赵立雨、师萍[1],俞立平、熊德平[2],张优智[3]。然而,大量文献中鲜有从周期波动视角分析二者之间的关系,改革开放三十多年来,财政科技投入周期和经济增长周期是否同步?周期运行分为几个阶段?每个阶段的持续期有多长?各个阶段之间相互转移的可能性又有多大?这些问题的回答有助于考察财政科技投入周期和经济周期的波动规律,挖掘引起财政科技投入周期和宏观经济周期波动的深层次原因,更有助于政府相关决策部门全面分析和解读当前与未来发展形势,优化政策组合,制定科学合理的科技和财政政策提供理论与实践依据。
鉴于传统线性计量方法在测度经济周期特征时存在诸多缺陷,刘金全等[4]等把经济增长过程简单地分为二区制状态:“扩张阶段”和“紧缩阶段”,陈浪南、刘宏伟[5]研究结果显著支持GDP增长率序列具有三区制状态:“低速增长阶段”,“适速增长阶段”和“高速增长阶段”。经济周期的研究思路当然也适用于对投资周期的分析,Harris et al[6]对美国教育投资周期特征进行了初步探讨,我国学者隋建利、刘金全[7]也发现中国财政教育投入周期分为“扩张阶段”和“衰退阶段”。
目前,在我国还没有发现基于马尔科夫区制转移模型研究财政科技投入周期与宏观经济周期协同性的相关文献。有鉴于此,本文借鉴上述学者的研究成果,基于改革开放以来财政科技投入和国内生产总值的年度数据,应用“三阶段”马尔科夫区制转移模型描述和刻画财政科技投入增长率和GDP增长率的阶段性变迁特征。通过“低速增长阶段”、“适度增长阶段”和“高速增长阶段”的区制划分以及区制转移概率的估算,探究财政科技投入与经济增长之间的多阶段动态演变关系,旨在对改革开放以来我国财政科技投入周期与经济周期的动态过程进行阶段性变迁识别和协同性分析。
2 研究方法与数据说明
为了捕捉和刻画财政科技投入和宏观经济的“阶段性”变迁特征,我们借鉴Hamilton的做法在自回归模型中引入参数的区制转移性质构建马尔科夫区制转移模型,具体形式如下:

εt|It-1~iidN(0,σ2(St))
(1)
其中,yt表示财政科技投入增长率或GDP增长率,μ是常数项,p是滞后阶数,εt为随机扰动项,It-1代表t-1时刻的信息集。模型(1)与简单自回归模型相比多了一个区制状态变量St,模型假设所有参数都依赖于状态变量St。在同一区制内,参数及方差不变,当区制发生转变时,参数及方差将随之变化。因此马尔科夫区制转移模型可以刻画和比较财政科技投入和宏观经济在不同阶段、状态或机制下所具有的特征。

(2)
其中,pij为状态变量St从t-1时刻i状态转移到t时刻j状态的概率,即:
pij=Pr(St=j|St-1=i),0 (3) 马尔科夫区制转移模型根据截距项、回归系数和方差项是否依赖于状态变量St而分为多种类型,可以依据AIC准则值较小和极大似然比统计量值较大的原则进行模型类型的选择。 本文采用1980—2012年中国财政科技投入(TCH)和国内生产总值(GDP)来描述科技投资周期和宏观经济周期的动态演变过程,数据来源于《中国科技统计年鉴》和《中国统计年鉴》。为了降低数据的波动性和异方差性,对两个变量取对数,分别使用LNTCH和LNGDP表示。 表1给出了变量的ADP单位根检验结果,从中可以看出LNTCH和LNGDP均是非平稳时间序列,但其一阶差分变量ΔLNTCH和ΔLNGDP在5%的显著水平下是平稳的。ΔLNTCH和ΔLNGDP是财政科技投入和GDP的增长率序列,可以准确刻画财政科技投入和GDP的相对变化,具有较好的经济含义。因此,本文将以财政科技投入增长率和GDP增长率作为研究对象。 表1 ADF单位根检验结果 注:Δ表示差分算子;检验形式为(c,t,k),其中c、t和k分别表示常数项、趋势项和滞后阶数(由AIC准则确定)。 本文采用带有MS-VAR模块的OX软件对模型进行估计,根据对数似然比统计量LogL尽可能大,AIC准则尽可能小的原则,确定模型形式为截距项、回归系数和方差项均依赖于状态变量St,滞后2阶的“三阶段”马尔科夫区制转移模型。表2与表3给出了模型参数、转移概率矩阵、区制持续情况以及检验统计量等具体估计结果。依据区制特征,将财政科技投入和GDP的波动周期划分为三个区制,区制1(St=1)表示“低速增长阶段”、区制2(St=2)表示“适速增长阶段”和区制3(St=3)表示“高速增长阶段”。 表2与表3列出的LR线性检验值分别为57.4987和67.0396,卡方统计量的伴随概率值均小于5%,显著拒绝线性关系的原假设。再者,诸如截距、自回归系数等大多数参数的估计结果都在5%的水平下显著,并且同一参数在不同区制下的估计结果差异较大。这些都说明非线性马尔科夫区制转移模型可以很好地刻画和捕捉财政科技投入周期和经济周期中阶段性变迁的动态过程,且低速增长阶段、适速增长阶段和高速增长阶段的三区制划分是较为合理且准确的。 由表2可知财政科技投入处于低速增长、适速增长和高速增长阶段的持续概率分别为0.9041、0.8653和0.9229,表现出较强的区制持续性。其中,高速增长阶段的稳定性最强,持续期(约13年)最长,发生频率(63.58%)最高,财政科技投入周期向该阶段转移的概率也最大,说明财政科技投入保持高速增长的可能性最高,在此阶段的抗风险能力最强;其次是低速增长阶段,较高的内在稳定性和持续期(约10年)决定需要较强的外力才能推动财政科技投入向高速增长阶段转移;最后是适速增长阶段,该阶段发生的频率(36.42%)仅次于高速增长阶段,但是持续期(约7年)最短。 表2 财政科技投入的马尔科夫区制转移模型估计结果 注:Δ表示参数在5%的水平下显著,小括号里是参数样本标准差。 由表3可知GDP处于低速增长、适速增长和高速增长阶段的持续概率分别为0.8471、0.9238和0.6628,说明适速增长阶段的内在稳定性最高,其次是低速增长阶段,最后是高速增长阶段。另外,各阶段对应的持续期分别为7年、13年和3年,虽然与同一阶段上财政科技投入的持续期之间存在着显著差异,但是GDP增长率处于低速增长阶段(适速增长阶段)的持续性与财政科技投入增长率处于适速增长阶段(高速增长阶段)的持续性相同,这为下文分析中确立的二者之间的“动态协同”关系提供了有力的支持。 对比分析财政科技投入与GDP的区制持续性可知,在低速增长和高速增长阶段,财政科技投入的持续性明显高于GDP 的持续性,即财政科技投入维持低速和高速增长的可能性强于GDP;而在适速增长阶段,财政科技投入的持续性明显低于GDP的持续性,即财政科技投入维持适速增长的可能性弱于GDP。因此,要充分重视财政科技投入更强的低速和高速增长持续性以及更弱的适速增长持续性特征,基于长期科学发展观,合理确定财政科技投入增长率,使其与中国GDP增速相适应,以期实现科技与经济的长期稳定健康发展。 表3 GDP的马尔科夫区制转移模型估计结果 注:Δ表示参数在5%的水平下显著,小括号里是参数样本标准差。 再者,分析财政科技投入增长率和GDP增长率的区制波动性。财政科技投入处于低速、适度和高速增长阶段的方差分别为0.0477、0.0289和0.0260(见表2),也就是说财政科技投入的波动性随着增长率水平的提升而逐步下降。同理,GDP处于低速、适度和高速增长阶段的方差分别为0.019、0.0347和0.005,在不考虑适速增长阶段的情况下,GDP的波动性也表现出随增长率水平提高而下降的趋势,而且方差水平均明显低于同一阶段上财政科技投入增长率的方差,表现出较低的不确定性。但是,GDP在适速增长阶段上的方差明显高于其他两个阶段以及该阶段上财政科技投入的方差。因此,当GDP处于适速增长阶段时,我们更应该注重宏观经济层面上的风险识别与预警,风险转移与分散,尽量维护宏观经济的平稳健康运行。 图1 财政科技投入处于低速增长阶段的平滑概率 图2 财政科技投入处于适速增长阶段的平滑概率 图3 财政科技投入处于高速增长阶段的平滑概率 图4 GDP处于低速增长阶段的平滑概率 图5 GDP处于适度增长阶段的平滑概率 图6 GDP处于高速增长阶段的平滑概率 为了便于分析财政科技投入周期与宏观经济周期的协同性,本文给出了财政科技投入和GDP在低速增长阶段(St=1)、适速增长阶段(St=2)和高速增长阶段(St=3)上的平滑概率图(见图1~图6)。平滑概率图可以清楚地展示经济变量在不同阶段发生概率转移的可能性,通常情况下,当区制状态变量St的概率值Pr(St=i|It-1)>0.5(i=1,2,3)时,就可以认为财政科技投入(或GDP)在t时刻处于i阶段。 纵观改革开放以来,财政科技投入周期和宏观经济周期的阶段性变迁轨迹,可以发现财政科技投入和GDP之间的周期波动关系大体上分为三个阶段。第一阶段从改革开放初到20世纪80年代末,为财政科技投入和宏观经济的非协同期。在此期间,GDP从低速增长阶段迈入适度增长阶段,但财政科技投入却始终处于低速增长阶段,这主要是由于改革开放伊始,国家将经济增长作为重点发展目标,在人力、资金和综合国力上对科技的支撑力度明显不足。第二阶段从20世纪90年代初到90年代中期,为财政科技投入与宏观经济的静态协同期。在此时期,财政科技投入和GDP均处于同一发展阶段,即高速增长阶段。原因在于经过改革开放后十年的努力与奋斗,中国经济增长步入了快车道,出现了明显的经济过热,导致了宏观经济层面上的风险加大,但也为增长财政科技投入奠定了坚实的经济基础,所以此阶段二者均保持高速增长态势。第三阶段从20世纪90年代中期至今,为财政科技投入与宏观经济的动态协同期。具体表现为伴随着GDP从低速增长阶段进入适速增长阶段,财政科技投入从适速增长阶段进入高速增长阶段,虽然同一时期所处阶段不同,但是动态走势和阶段跨度完全一致。在此期间,中国经济于1995年实现“软着陆”,进入低速增长时期,直到2004年后才回暖,迈入适速增长阶段,与此同时,世界经济运行状况以及中国“稳增长”的宏观调控政策取向决定GDP进入高速增长阶段的可能性极小;另一方面在中国追求经济增长方式转变与经济增长质量提升的背景下,国家对科技的重视程度和投入总量逐年提升,因此导致财政科技投入所处阶段明显高于同期的GDP。 此外,进一步分析财政科技投入周期与宏观经济周期在协同期内的“时间一致性”问题,我们发现与财政科技投入周期相比较,宏观经济周期具有一定的“时间滞后性”。在静态协同期内,财政科技投入于1991 年步入高速增长阶段,而GDP则滞后1年,于1992年才步入高速增长阶段;在动态协同期内,财政科技投入在2003年从适速增长转为高速增长,而GDP依然滞后1年在2004年才由低速增长转为适速增长,也就是说中国财政科技投入是超前发展来支撑宏观经济的增长,该结论符合经济增长理论和中国的具体实践。 (1)转移概率矩阵估计结果表明财政科技投入处于高速增长阶段的稳定性最强,而处于适速增长阶段的稳定性最弱;GDP处于适度增长阶段的稳定性最高,而处于高速增长阶段的稳定性最低。比较而言,财政科技投入维持低速增长和高速增长的可能性强于GDP,而维持适速增长的可能性弱于GDP。因此,要充分重视财政科技投入更强低速增长和高速增长持续性以及更弱适速增长持续性的特征,基于长期科学发展视角,合理确定财政科技投入的增长速度,使其与中国GDP增速相适应。 (2)样本方差估计结果说明财政科技投入的波动性随着增长率水平的提升逐步下降;在不考虑适速增长阶段的情况下,GDP的波动性也表现出同样的特征,而且明显低于同一阶段上财政科技投入的波动性。但GDP在适速增长阶段上表现出较高的不确定性,因此,我们更应该提高此阶段上GDP的风险识别与预警力度,保持宏观经济平稳健康运行。 (3)平滑概率估计结果印证财政科技投入在1981—1989年间处于低速增长阶段,1995—2002年间处于适速增长阶段,在1990—1994年与2003—2012年间处于高速增长阶段。GDP在1981—1983年与1995—2003年间处于低速增长阶段,1984—1990年与2004—2012年处于适速增长阶段,在1991—1994年处于高速增长阶段。而且,近八年来,中国财政科技投入表现出较高的风险防范或转移能力,整体运行态势高速且平稳,但GDP层面上的风险防御与阻隔、风险分散与转移能力还不够完善,风险管理能力亟需进一步提升。 (4)平滑概率图显示20世纪 90 年代初期是财政科技投入周期与宏观经济周期同步与否的“分水岭”。改革开放初期到20世纪80年代末是财政科技投入和宏观经济的“非协同期”,在此期间GDP从低速增长阶段进入适度增长阶段,但是财政科技投入一直处于低速增长阶段;20世纪90年代初到90年代中期是财政科技投入与宏观经济均处于高速增长阶段的静态协同期;从20世纪90年代中期至今是财政科技投入与宏观经济动态走势与阶段跨度完全一致的动态协同期,即伴随着GDP从低速增长阶段进入适速增长阶段,财政科技投入从适速增长阶段迈入高速增长阶段。 纵观改革开放后30多年的科技事业与宏观经济发展历程,自始至终都体现出宏观经济发展是财政科技投入的基础和保障。在改革开放伊始的10年里,中国工作重心集中在经济增长上,科技发展放在的次要地位,经济实力和综合国力的欠缺造就了“经济增长提速,财政科技投入却保持低位徘徊”的特殊局面。在随后5年里,中国经济迅猛发展,进入了高速增长的“过热期”,与此同时,财政科技投入也摆脱了10年的低速增长态势,进入高速增长期。自此之后,经济实力的增强为科技发展奠定了坚实的物质基础,加之政府对科技发展的日益重视,使得中国财政科技投入增长率始终保持与GDP增长率同向运行,而且一直处在高于同期GDP增长率的水平上。 与此同时,我们还要注重科技进步对宏观经济的反作用力,科学技术的发展不仅可以提升经济运行效率,增加个人收入和企业利润,提升GDP总量,还可以改善GDP质量。目前,无论是发达国家还是发展中国家,都在加大科技投入力度,大幅增加科技投入成为很多国家提升竞争力的国家战略[8]。虽然近些年来,中国财政科技投入增速大幅提升,且保持了良好的发展态势,但是财政科技投入量和发达国家相比仍然存在着较大差距。就财政科技投入资金占研究与试验发展(R&D)总经费的比重来说,美国为31.3%(2009年),英国为32.1%(2010年),法国为39.7%(2010年),加拿大为34.3%(2009年),然而中国只有21.7%(2011年),远低于发达国家35%左右的平均水平。因此,中国应该继续加大财政科技投入,并维持财政科技投入优先发展推动GDP增长的发展模式,同时注重GDP层面上的风险甄别与转移,努力营造出以科技发展促进经济增长,以经济增长保障科技投入的良好局面。 [1]赵立雨,师萍.政府财政研发投入与经济增长的协整检验[J].中国软科学,2010,(2):53-58. [2]俞立平,熊德平.财政科技投入对经济贡献的动态综合估计[J].科学学研究,2011,(11):1651-1657. [3]张优智.科技投入与经济增长:存在门限的非线性关系[J].中国科技论坛,2014,(5):32-38. [4]刘金全,刘志刚,于冬.我国经济周期波动性与阶段性之间关联的非对称性检验——Plucking模型对中国经济的实证研究[J].统计研究,2005,(8):38-43. [5]陈浪南,刘宏伟.我国经济周期波动的非对称性和持续性研究[J].经济研究,2007,(4):43-52. [6]Harris R G,Robertson P E,Xu J Y.The International Effects of China’s Growth,Trade and Education Booms[J].The World Economy,2011,(34):1703-1725. [7]隋建利,刘金全.改革开放以来我国教育投资周期与宏观经济周期同步吗——基于“双阶段”马尔科夫区制转移模型的实证分析[J].教育与经济,2013,(5):3-12. [8]陈春晖,曾德明.我国自主创新投入产出实证研究[J].研究与发展管理,2009,(2):18-23. (责任编辑 刘传忠) Synchronization between Financial Technology Investment Cycle and Economics Cycle Based on Markov Regime Switching Model Pan Fanghui,Li Cuixia,Fan Bin (School of Economics and Management,Northeast Agricultural University,Harbin 150030,China) Based on three-stage Markov regime switching model,regimes identification and synchronization analysis were made to analyze the dynamic process of China’s financial technology investment cycle and economic cycle since reform and opening up.The empirical results show that:financial technology investment cycle and GDP cycle contain three stages named low growth,moderate growth and the high growth phase,which switches with probability;financial technology investment has stronger persistence and volatility in the low growth and high growth phase than GDP on the same stage,and has weaker persistence and volatility in the moderate-growth phase than GDP on the same stage;the early 1990’s is the watershed to judge if financial technology investment cycle and GDP cycle is synchronized or not.Before this prior,financial technology investment cycle and the GDP cycle is non-synchronized;and after this,financial technology investment cycle and the GDP cycle exhibit static synchronization relationship,and then shows dynamic synchronization relationship,but GDP cycle has a certain time lag compared with financial technology investment cycle. Financial technology investment cycle;Economics cycle;Synchronization;Markov regime switching model 中国博士后科学基金项目(2013M540267),国家自然基金面上项目(71173035),国家自然基金青年项目(71303039)。 2014-07-31 潘方卉(1982-),女,黑龙江克东人,东北农业大学经济管理学院讲师;研究方向:科技政策管理。 F062.3 A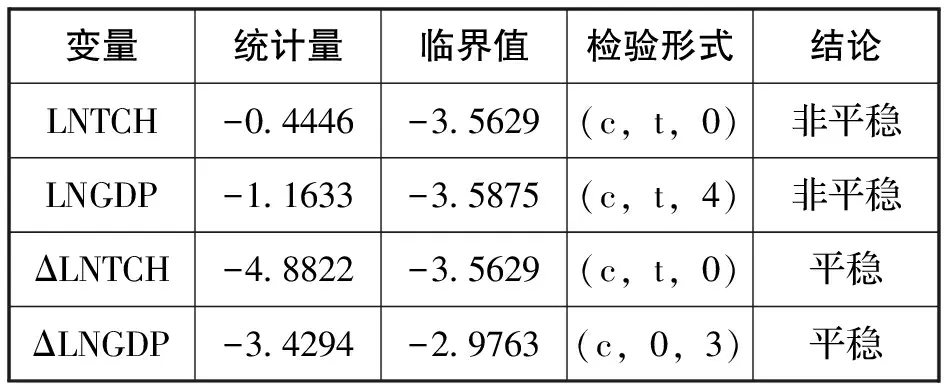
3 模型估计结果与分析
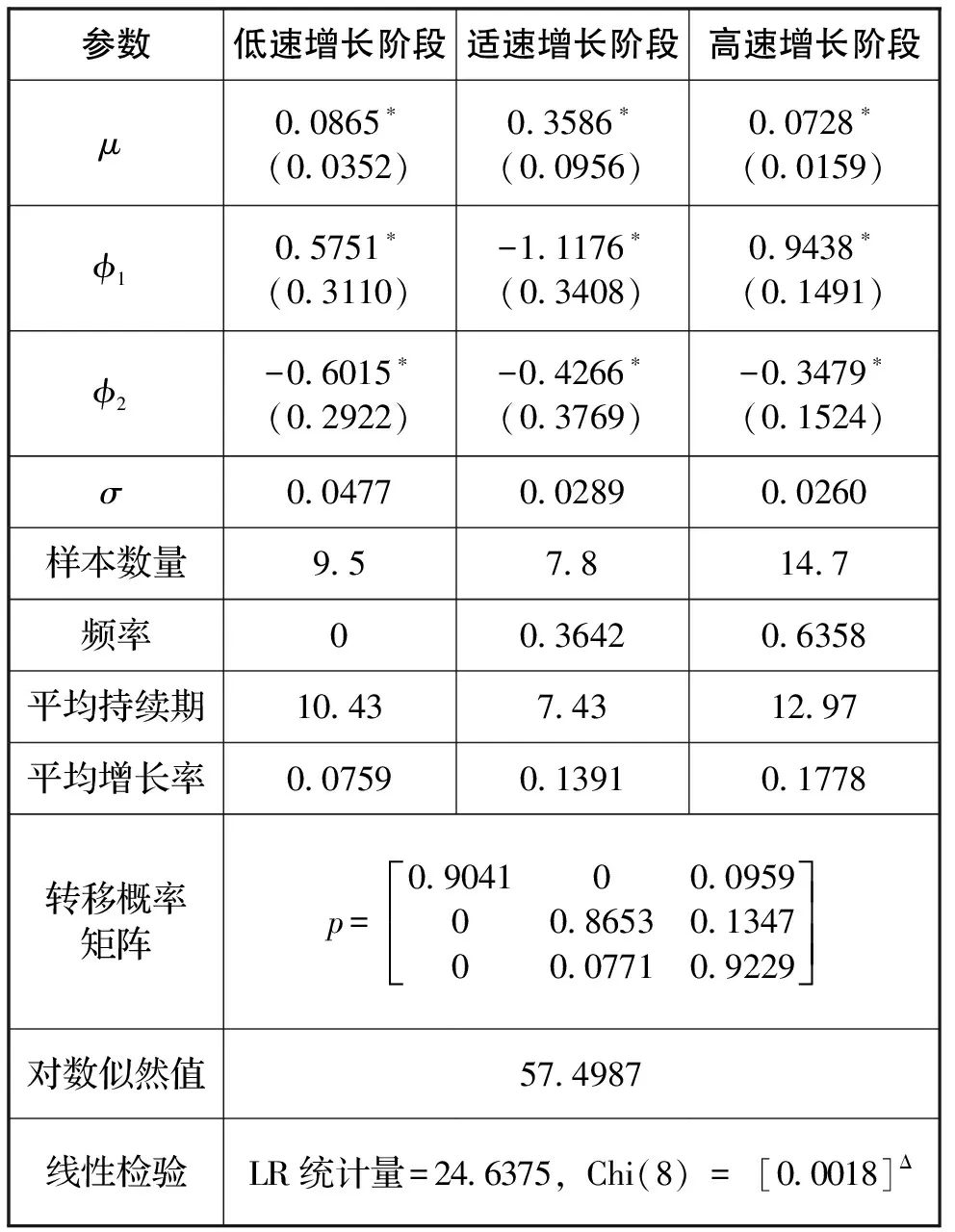

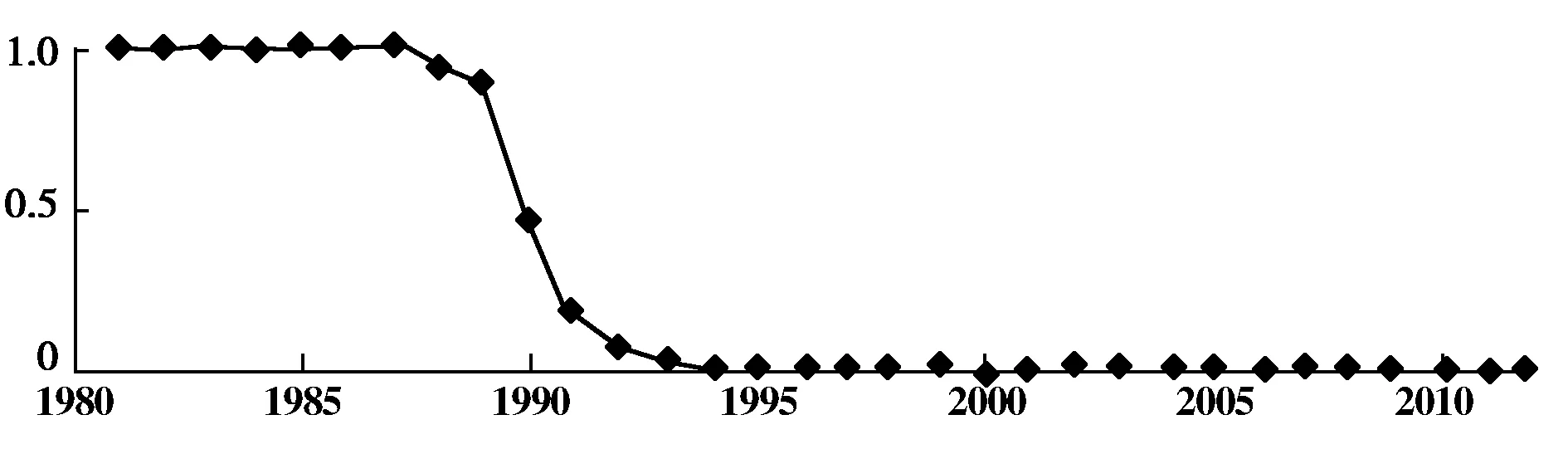



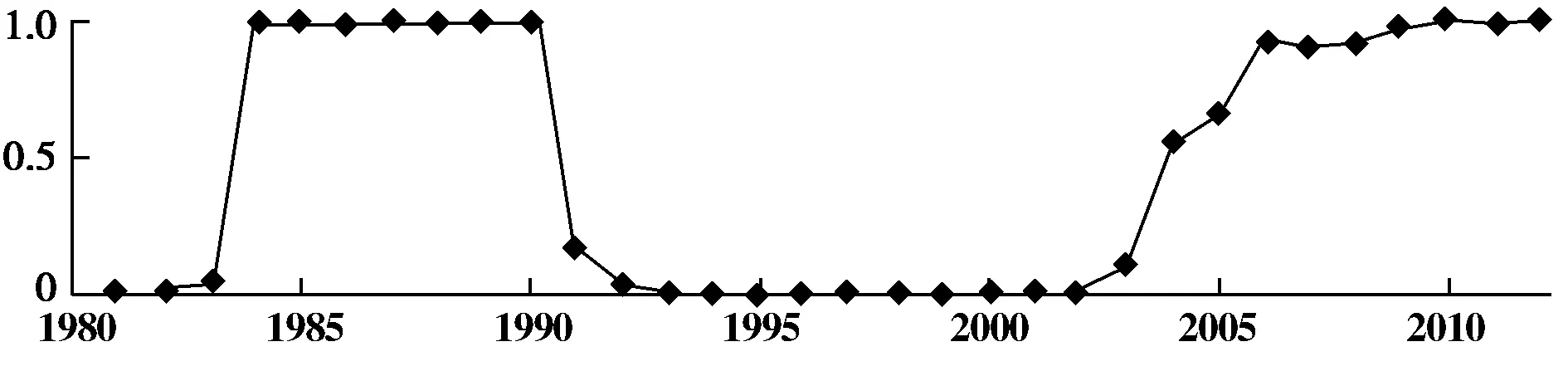

4 结论与启示
