四旋翼飞行控制系统的设计与研究

王晓初 卢 琛

(广东工业大学机电工程学院，广东 广州 510006)

四旋翼飞行控制系统的设计与研究

王晓初 卢 琛

(广东工业大学机电工程学院，广东 广州 510006)

四旋翼飞行器以其结构简单、运动灵活和操控方便等优点，被广泛应用于各个领域，它具有二阶系统所包含的不稳定性、非线性和较强的耦合性等典型特点。控制系统是四旋翼飞行器设计的难点。针对这一问题，设计以STM32微控制器为硬件平台的控制系统，并搭载μC/OS-II嵌入式系统，结合惯性传感器与互补滤波算法，实现对四旋翼的串级PID控制。试验结果表明，该控制系统具有较强的鲁棒性，对四旋翼具有良好的控制效果。

四旋翼飞行器 互补滤波器 姿态解算 STM32 μC/OS-II PID

0 引言

无人机是当今航空领域研究的热点，而微小型无人机则更是世界无人机发展的重要方向之一。四旋翼作为微小型无人机的一类，具有结构简单、运动灵活等优点，无论是在民用还是在军用领域，都具有很高的利用价值[1]。

不同于其他种类的无人机，四旋翼在控制上具有低阻尼、非线性和多耦合等特点，其控制系统是四旋翼设计的关键[2]。文献[3]给出了四旋翼的飞行原理与硬件架构，其模块化的硬件组成有利于系统维护。文献[4]和[5]给出了一种捷联式惯性导航算法，从理论上分析了姿态解算的实现。文献[1]给出了一种基于互补滤波器的姿态修正算法，为无人机的精确导航提供了方向。本文则结合模块化设计的思路，以μC/OS-II操作系统为软件平台，采用互补滤波器与串级PID算法，设计了一种四旋翼的控制系统。

1 硬件系统的设计

系统采用意法半导体公司的32位微控制器STM32作为控制核心，其最高运行主频可达72 MHz，满足整个控制系统对实时性的要求。姿态检测传感器采用集成有陀螺仪和加速度仪的惯性元件MPU6050，避免了组合传感器之间的安装误差。数据传输设备采用2.4 Gbit/s无线传输模块NRF24L01，可以实现飞行数据的快速传输。系统整体架构如图1所示。

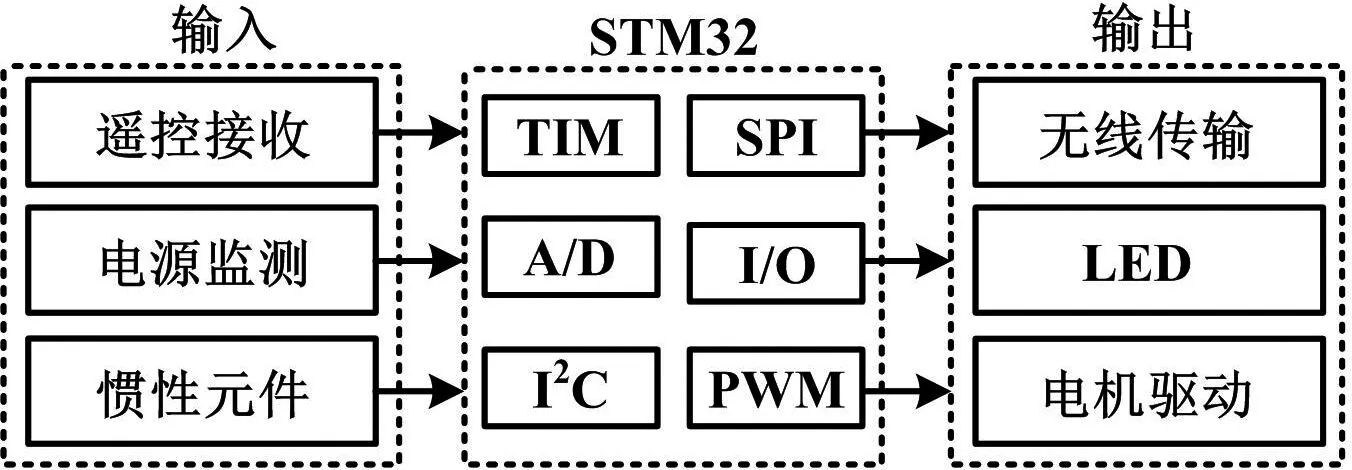
图1 四旋翼的硬件架构Fig.1 The hardware architecture of the quadrotor

图1中，遥控设备、电源监测和惯性元件是控制器的输入设备，主要负责控制信号与姿态信号的采集;无线传输模块、电机驱动和LED作为控制器的输出设备，主要负责与外界的联系与控制。

2 软件的设计

采用μC/OS-II操作系统作为软件平台[6]，有利于模块化设计，便于系统设计与维护，其流程框图如图2所示。

其中，初始化操作最先完成，为操作系统的运行做前期的准备工作。系统时钟由STM32滴答计时器产生，为操作系统提供有序的控制节拍，而任务的创建则是具体任务的分工，并且由操作系统掌控任务之间的协同与调度。

在设定任务中，采样任务优先级最高，主要完成输入设备的数据采集与飞行姿态解算工作，姿态的解算直接影响着飞行器的控制输出。控制任务是系统的核心，其根据姿态输出与期望输出构成姿态偏差，并以此控制电机输出而达到预期效果。通信任务与主循环任务分别负责与外界的数据传递和状态显示等实时性要求不高的操作。

2.1 四旋翼飞行器的姿态解算

姿态解算由陀螺仪和加速度传感器通过融合算法得到稳定、准确和实时的姿态角。常用的融合算法有欧拉角法、方向余弦法和四元数法。姿态角由欧拉角表示，可直接作为PID的控制量。但用欧拉角进行姿态解算存在大量三角函数，且俯仰角为±90°时方程会出现奇点。方向余弦法求解姿态避免了欧拉角方程退化的现象，可以实现全姿态解算，但是方向余弦有9个参数，解算9个微分方程工作量大。相对于方向余弦法，四元数法则计算量小了很多，同时可以避免奇异现象[7]。

四元数是由1个实数和3个虚数构成的超复数，

表示为[q]=q0+q1i+q2j+q3k，其中，q0、q1、q2、q3是实数，i、j和k既是互相正交的单位向量，又是虚单位。因此，四元数既可以看作四维空间中的向量，又可看作超复数。

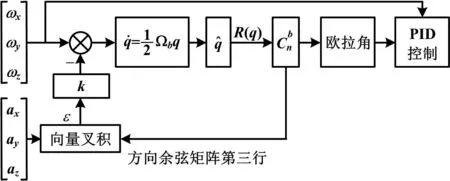
图3 姿态解算流程图Fig.3 Flowchart of posture algorithm

四元数微分方程矩阵形式如下：

式中：ωbx、ωby、ωbz分别为惯性传感器绕参考坐标系测量的角速度。

将其近似为一阶差分形式，有：

令ΔΘ=ΩbΔt，则求解四元数微分方程的迭代格式为：

(1)

由欧拉角表示导航坐标系[xn]到载体坐标系[xb]的余弦矩阵，即[8]：

(2)

θ=-arcsinC13

(3)

(4)

另外，由四元数表出导航坐标系[xn]到载体坐标系[xb]的余弦矩阵为[8]：

设陀螺仪更新姿态为qg，加速度计更新姿态为qc，其对应的测量噪声分别为ξ1和ξ2，则有修正简化模型如图4所示。

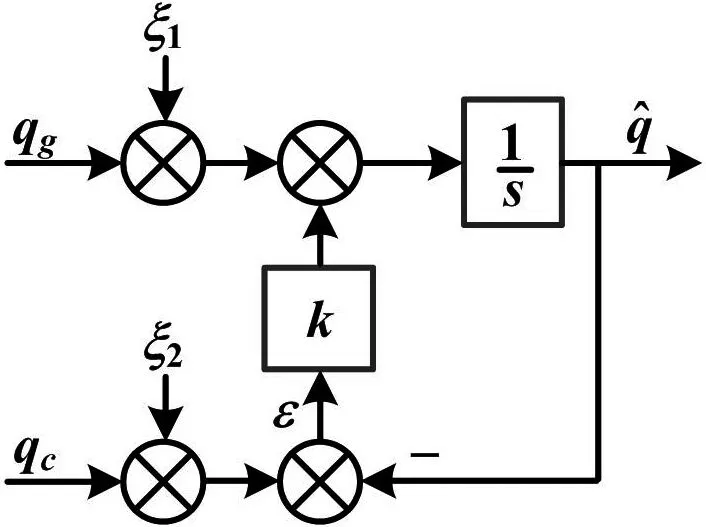
图4 姿态修正简化模型Fig.4 The simplified model of posture correction

其噪声传递函数分别为[9]：

(5)

(6)

式(5)和(6)可以用来设计k的取值，并以此确定互补滤波器的截断频率fτ[1]。图5所示为此互补滤波器在k=0.02时的俯仰角测试数据。

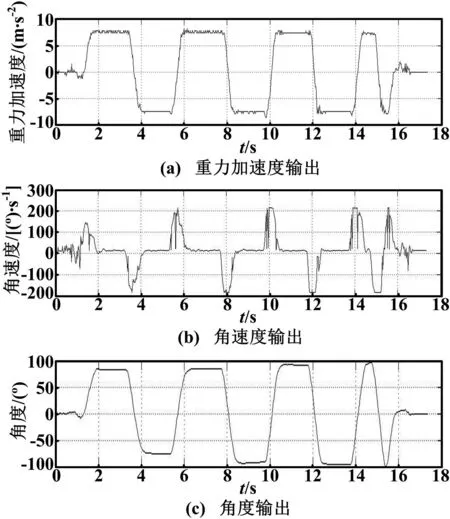
图5 互补滤波器输出Fig.5 Outputs of the complementary filter

2.2PID控制器的设计

PID控制流程如图6所示，整个控制回路分为角度环和角速度环。角速度环采用P控制，其作用是产生阻尼效应，抵抗干扰，使得被控系统G(s)更加稳定[11]。角度环采用PI控制，实时姿态与目标姿态构成偏差，对偏差进行PI控制，可使得四旋翼稳定在指定位置[6]。

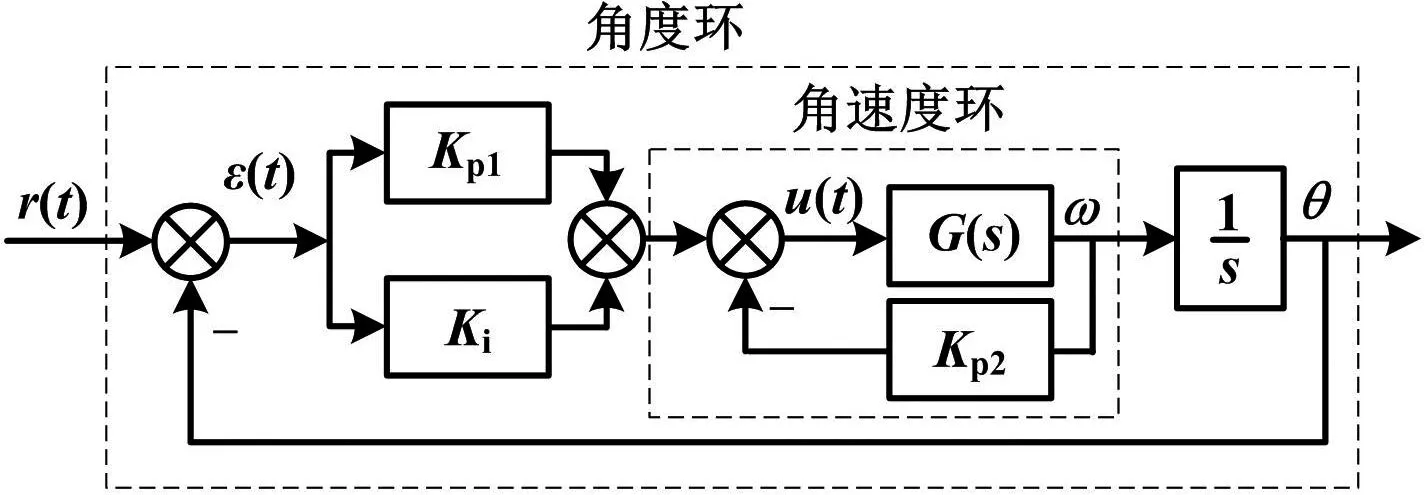
图6 PID控制框图Fig.6 Block diagram of PID control

采用位置式PID控制器，则角度环和角速度环的控制律分别为：

(7)

uω(k)=Kp2ω

(8)

式中:ε(k)为期望姿态与当前姿态的误差;输入参数ω为陀螺仪测量的角速度向量。

则整个串级PID控制器输出为：

(9)

如图7所示，为四旋翼在单轴悬停状态下，通过无线模块实时传输其X轴的加速度、角速度和姿态角度偏差的输出数据。

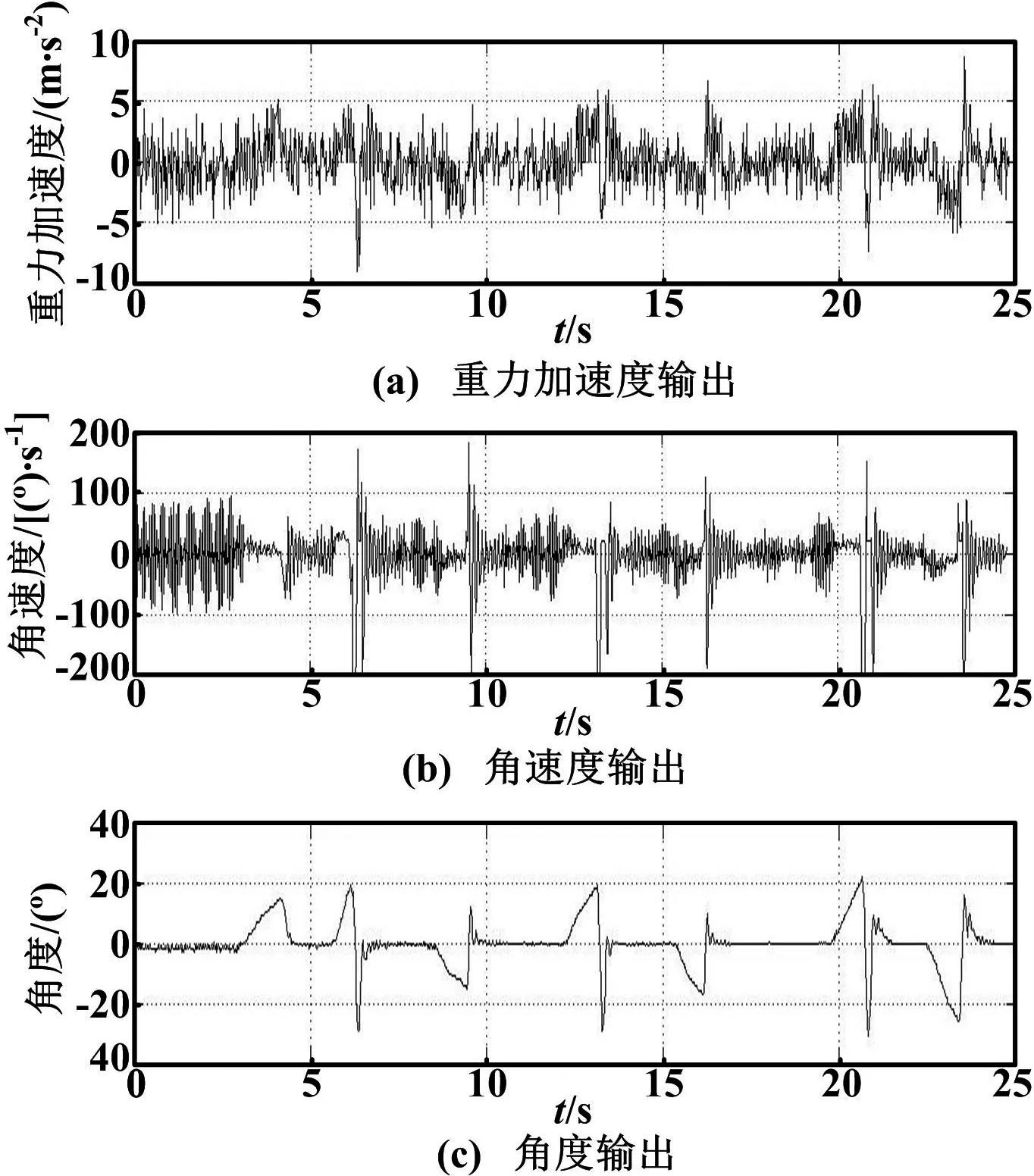
图7 悬停状态时X轴方向的输出Fig.7 The outputs of the X axis direction in hovering state

如图7所示，在未引入干扰的状态下，角度偏差基本维持在零度左右;为检验控制器的稳定性而引入外界干扰，可以看到干扰消除后，角度偏差在控制器作用下迅速收敛到零度附近，说明此控制器效果明显，基本达到预期设定要求。

3 结束语

采用μC/OS-II操作系统作为整个系统的构建平台，为硬件的模块化架构和软件的模块化设计提供了条件，不仅有利于系统的设计与维护，而且在实际应用中更有利于硬件的测试与软件的移植。在控制算法上采用串级PID控制，将整个控制回路分为两个控制环，其中角度环负责回正自稳，角速度环负责抵抗外界干扰，这样有利于试验参数的设计与调整。在姿态解算方面采用组合传感器与融合算法，互补融合陀螺仪的高频特性与加速度仪的低频特性，结合四元数微分方程可以实现较高精度的全角度解算。

[1] 梁延德,程敏.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统,2011(11):56-58,61.

[2] 刘峰,吕强.四轴飞行器姿态控制系统设计[J].计算机测量与控制,2011(3):583-585,616.

[3] 郭晓鸿,杨忠.一种基于STM32的四旋翼飞行器控制器[J].应用科技,2011(7):35-40.

[4] 张荣辉.基于四元数法的捷联式惯性导航系统的姿态解算[J].光学精密工程,2008(10):1963-1970.

[5] Fresk E，Nikolakopoulos G.Full quaternion based attitude control for a quadrotor[C]//Control Conference(ECC),2013 European,2013:17-19.

[6] 任哲.嵌入式实时操作系统μC/OS-II原理及应用[M].3版.北京：北京航空航天大学出版社，2014.

[7] 胡庆.基于STM32单片机的无人机飞行控制系统设计[D].南京：南京航空航天大学,2012.

[8] 夏喜旺.关于大角度范围内四元数与欧拉角转换的思考[J].导弹与航天运载技术,2012(5):47-53.

[9] 高钟毓．惯性导航系统技术[M].北京：清华大学出版社，2012.

[10]Bachmann E R.Orientation tracking for humans and robots using inertial sensors[C]//Computational Intelligence in Robotics and Automation,CIRA′99.Proceedings.1999 IEEE International Symposium on.1999.

[11]许震,毛丽民.四轴飞行器控制系统设计[J].常熟理工学院学报,2013(2):109-113.

Design and Research on the Flight Control System for Quadrotor

The quadrotor features many advantages, e.g., simple structure, flexible movement and ease operation, etc., so it has been widely applied in various areas. While it also possesses the typical characteristics of second order system, including unstable, non-linear and stronger coupling, thus control system is its design difficulty. Aiming at these problems, the control system is designed with STM32 microprocessor as hardware platform and equipped the μC/OS-II embedded system, the PID cascade control for quadrotor is implemented by combining the inertial sensors and complementary filtering algorithm. The experimental results indicate that this control system possesses stronger robustness and excellent effect for quadrotor.

Quadmotor Complementary filter Posture solver STM32 μC/OS-II PID

王晓初(1964-)，男，1989年毕业于湖南大学电控制专业，获硕士学位，副教授；主要从事机械电子方向的研究。

TP273

A

10.16086/j.cnki.issn1000-0380.201506002

修改稿收到日期：2014-12-24。