善于捕捉学习信息 优化初中数学课堂教学

闭海英

【关键词】学习信息 初中数学 课堂教学 优化策略

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2015）04A-

0072-01

信息反馈是促进教学过程不断优化、实现课堂教学效率不断提高的重要手段。如何在有限的45分钟内获得准确、具体的反馈信息，掌握各层次学生的学习状态，需要教师以一个合理的计划做到善于捕捉、收集反馈信息，随时调节教学进程，从而更加高质高效地完成教学任务。下面，笔者就结合教学实例，从三方面论述在初中数学课堂教学中对反馈信息的收集与利用。

一、在课堂巡视中捕捉即时信息

课堂巡视贯穿于整个课堂教学中，是教师获取学生思维过程最重要的一种信息反馈途径。教师利用这些反馈信息可以客观地对学生进行指导，以此来弥补课堂教学的缺陷。因此，教师的巡视并不是走过场，而要时刻关注学生的学习动态以及在学习中遇到的问题，如学生在思考时、练习时、做题时遇到的无法解决的问题，教师可以立即捕捉到不可预知的“生成”，从而及时改进教学方法，提高课堂教学的高效性。

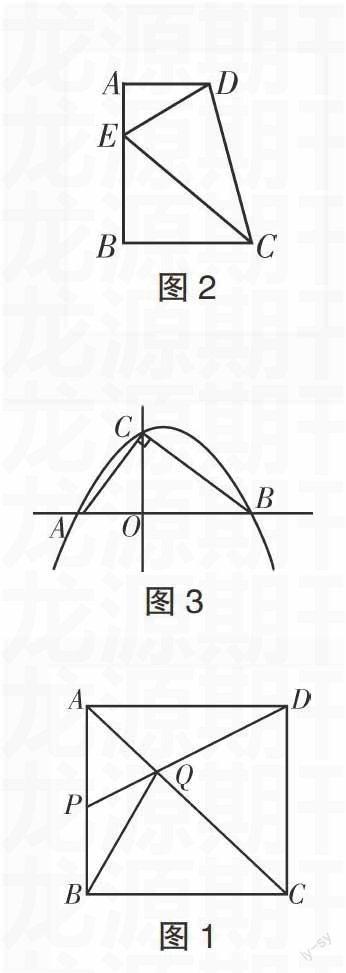
例如，（如图1）在边长为4的正方形ABCD中，AB线上的P点从A向B点移动，连接PD、AC，使DP、AC两条线相交于Q点，连接BQ。①试证明：P点在AB线上移动到什么位置时，都能使△ABQ≌△ADQ。②如何使P点在AB线上移动，才能让正方形ABCD的面积成为三角形△ADQ的六倍？

笔者在课堂巡视中发现有学生在解决问题②时不知从何入手，于是笔者提示：我们在解△ADQ面积时，把哪一条边作为底最为简单呢？学生思考后回答：AD边。紧接着笔者又问：AD边上的高应达到什么条件时才能使△ADQ的面积是正方形ABCD的六分之一？能不能先求出高的长度呢？AP线的长度可以解出来吗？

上述问题对于学习能力较强的学生来说，是相对容易解决的，于是笔者加深了问题的深度：在P点移动到什么位置时可以使△ABQ成为等腰三角形？这样，教师在课堂巡视的过程中既可以照顾“潜力”生的学习情况，又能满足优秀生的学习需求，使学生得到不同程度的发展。

二、在课堂提问中捕捉即时信息

课堂提问可以调动学生思考问题的积极性，它是构建课堂信息输出与反馈的桥梁。在提问中教师不但要善于提问，而且要会问，通过多方面、多层次、多角度的提问，发现学生在回答问题时暴露出的错误，从而及时作出相应的课堂调整或采取针对性的补救。

例如，在教学《相似三角形》时，笔者布置了下列练习题。如图2所示，在直角梯形ABCD中，直线AD平行于BC，∠A=90°，∠B=90°，∠CED=90°，那么试论证DA、EA、EB、CB四条线段之间的关系？学生在分析图形时发现四条线段是成一定比例的，紧接着笔者提问：“现在要把这三个成90°的直角改为60°，上述问题中的四条线段又是什么关系呢？”学生依然用第一步中找相等角的办法，求证出角ADE与角BEC相似，从而得出四条线段的关系——成比例。

接着笔者又问：“把60°角换成130°呢，还能够得出上述相同的结论吗？”学生们在交流讨论后肯定地回答“可以”。笔者让一位学生回答：“只要∠EAD=∠CED=∠CBE，线段AD、AE、BE、BC都是成比例的。”在这里，笔者运用另一种方式进行提问，让学生进一步了解图形的特点，进而开拓了探究问题的思路。

三、从课堂练习中捕捉即时信息

知识的巩固离不开练习环节。教师应围绕每一节课的教学重难点或是某一单元的知识点精心设计练习题型，通过练习查漏补缺，将学生对知识的一知半解暴露出来，让教师对后续教学做到更为科学、合理地安排设计，实现知识的系统化。

例如，在复习抛物线中的直角三角形的内容时，笔者首先问学生关于Rt△ABC，你知道哪些知识？然后在此基础上，提问：①在Rt△ABC中，如果CO⊥AB于O，那么你能得到什么结论？②以AB所在直线为x轴，以CO所在的直线为Y轴，建立直角坐标系，若CB=2，AC=，请写出A，B，C三点的坐标。③如图3所示，如果一抛物线过A，B，C三点，求它的解析式？

通过设计层层递进的题型，不断强化学生对抛物线中的直角三角形的理解，这不仅有利于学生温故知新，也能在复习强化中锻炼学生的发散思维，提高学生解决问题的能力。

（责编 林 剑）