一阶常微分方程具有乘积形式积分因子的存在条件及应用
2015-06-10李耀红
李耀红,王 琳
1.宿州学院数学与统计学院,安徽宿州,234000;2.许昌幼儿师范学校,河南许昌,461700
一阶常微分方程具有乘积形式积分因子的存在条件及应用
李耀红1,王 琳2
1.宿州学院数学与统计学院,安徽宿州,234000;2.许昌幼儿师范学校,河南许昌,461700
讨论了一阶常微分方程M(x,y)dx+N(x,y)dy=0的求解问题,给出了方程具有一类形如f(a1xα1+b1xs1yt1+c1yβ1)g(a2xα2+b2xs2yt2+c2yβ2)乘积形式积分因子的充要条件,并结合实例讨论它的应用。该结果推广了相关文献的结论。
一阶常微分方程;乘积形式积分因子;全微分方程
1 问题的提出
全微分方程是一阶常微分方程中一类重要的方程。通常只要利用某些特定条件,判定某个一阶微分方程为全微分方程,其通解就能直接由公式给出。因此寻找一阶常微分方程:
M(x,y)dx+N(x,y)dy=0
(1)
的积分因子μ(x,y),使得一阶常微分方程:
μ(x,y)M(x,y)dx+μ(x,y)N(x,y)dy=0
成为全微分方程,是一种求解方程(1)简单实用的方法。
对一些具有简单特殊形式积分因子存在性条件,文[1-4]进行了讨论;文[5-8]则对一些复合型积分因子的存在性定理和计算公式进行了探讨;文[9-11]讨论几类具有乘积形式的积分因子问题求解。结合上述文献的研究结果,本文讨论方程(1)具有一类形如
f(a1xα1+b1xs1yt1+c1yβ1)g(a2xα2
+b2xs2yt2+c2yβ2)
(2)
乘积形式积分因子存在的充要条件,它更具一般性,并结合实例说明上述形式因子的求解。
2 主要定理
引理[1]:连续可微函数μ(x,y)≠0为方程(1)的积分因子的充要条件是:(μM)y=(μN)x。
定理1 方程(1)具有形如(2)的乘积形式积分因子的充要条件是:
(My-Nx)/{f′(z1)g(z2)[N(a1α1xα1-1+b1s1xs1-1yt1)-M(b1t1xs1yt1-1+c1β1yβ1-1)]+f(z1)g′(z2)×[N(a2α2xα2-1+b2s2xs2-1yt2))-M(b2t2xs2yt2-1+c2β2yβ2-1)]}=1/f(z1)g(z2)
(3)
其中ai,bi,ci,αi,βi,si,ti是任意常数,且zi=aixαi+bixsiyti+ciyβi,i=1,2。
证明:由引理1知,式(2)是方程(1)的乘积形式积分因子的充要条件是:
(fgM)y=(fgN)x
即有:
fygM+fgyM+fgMy
=fxgN+fgxN+fgNx
故有:
f′(z1)(b1t1xs1yt1-1+c1β1yβ1-1)g(z2)M+f(z1)g′(z2)(b2t2xs2yt2-1+c2β2yβ2-1)M+f(z1)g(z2)My=f′(z1)(a1α1xα1-1+b1s1xs1-1yt1)g(z2)N+f(z1)g′(z2)(a2α2xα2-1+b2s2xs2-1yt2)N+f(z1)g(z2)Nx
整理后立即得(3)式,于是定理1得证。
注1:在定理1中,若令g(z2)=1,即得文[2]中定理1;若令a1=c1=b2=0,即得文[9]中的定理1;若令a1=c1=1,b1=0,可得文[10]定理1。若令b1=b2=0,即得文[11]中的定理1。故本定理推广了多个相关文献结果。
推论1 若存在函数F(z1)使得等式:
(My-Nx)/[N(a1α1xα1-1+b1s1xs1-1yt1)
-M(b1t1xs1yt1-1+c1β1yβ1-1)]=F(z1)
下面给出方程(1)具有形如(2)的乘积形式积分因子的求解方法。
定理2 若方程:
g(z2)M(x,y)dx+g(z2)N(x,y)dy=0
(4)
满足
{g(z2)(My-Nx)+g′(z2)[M(b2t2xs2yt2-1+c2β2yβ2-1)-N(a1α1xα1-1+b1s1xs1-1yt1)]}/g(z2)
×[N(a1α1xα1-1+b1s1xs1-1yt1)-M(b1t1xs1yt1-1+c1β1yβ1-1)]=F(z1)
(5)
则方程(4)具有积分因子:
于是方程(1)具有积分因子:
证明 将推论1中M(x,y)和N(x,y)分别用g(z2)M(x,y)和g(z2)N(x,y)代入计算直接可得结果(5)。
注2:将(5)式重新整理可得:
观察可知,通过选取恰当的函数F(z1)可确定出函数f(z1),进而求出原方程的积分因子。
从注2中可以得到求乘积形式积分因子(2)的具体求法,即简化为如下两个步骤完成:
i)从满足(5)式推导出函数g(z2)要满足的关系式, 取合适的F(z1), 确定g(z2);
ii)求方程(4)具有形如f(z1)的积分因子,确定方程(1)的积分因子f(z1)g(z2)。
2 应用举例
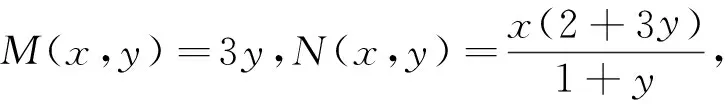
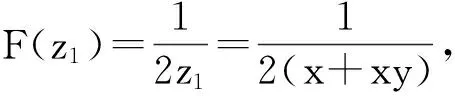
[1]王高雄,周之铭,朱思铭,等.常微分方程[M].北京:高等教育出版社,2006:39-46
[2]陈明玉.一阶常微分方程形如μ(axα+bxsyt+cyβ)积分因子的充要条件[J].大学数学,2005,21(1):130-133
[3]张玮玮.关于一类特殊一阶常微分方程积分因子的探讨[J].安庆师范学院学报,2014,20(2):10-11
[4]王景艳.几类特殊积分因子存在的充要条件及其应用[J].保山学院学报,2014,33(2):53-55
[5]李耀红,张海燕.几类微分方程的积分因子存在定理[J].巢湖学院学报,2006,8(3):8-9
[6]李耀红,陈浩.对微分方程复合型积分因子问题的推广[J].黄山学院学报,2006,8(3):11-12
[7]张海燕,戴扬,陈洁.新复合型积分因子的存在定理及应用[J].皖西学院学报,2007,23(2):7-9
[8]陈星海,李璜,韩祥临.三类复合型积分因子的充分必要条件及其应用[J].湖州师范学院学报,2010,32(2):44-49
[9]彭艳芳,黄春妙.一阶常微分方程具有乘积形式形如f(xαyβ)g(axs+byt)积分因子的求解[J].孝感学院学报,2008,28(6):33-34
[10]徐彬.一阶常微分方程具有一种乘积形式积分因子的求解[J].黄冈师范学院学报,2009,29(3):13-15
[11]韩祥临,陈星海.一类积分因子的存在条件及应用[J].高等数学研究,2012,15(3):11-12
(责任编辑:汪材印)
10.3969/j.issn.1673-2006.2015.09.025
2015-06-20
安徽省省级专业综合改革试点项目“数学与应用数学专业综合改革试点”(2012zy46);宿州学院校级校企合作实践教育基地项目“综合理科实践教育基地”(szxysjjd201205)。
李耀红(1978-),湖北武汉人,硕士,副教授,主要研究方向:常微分方程。
0175.1
A
1673-2006(2015)09-0093-02
