基于电流观测与重复控制的逆变器多环控制策略研究

吕世轩，郑丽君，宋建成，都海龙，马海霞

（1.太原理工大学煤矿电气设备与智能控制山西省重点实验室，山西太原030024；2.太原理工大学电气与动力工程学院，山西太原030024；3.山西晋煤集团技术研究院有限责任公司，山西晋城048000）

近年来，PWM 电压型逆变器已广泛应用于交流稳压器（AVR）、不间断电源（UPS）、可编程交流电源（PACS）等场合，这些场合均要求其输出兼具快速动态响应、高精度稳态波形和抗扰动能力强等特性［1］。目前已有的逆变器控制策略，如经典PID 控制、双闭环控制、状态反馈控制等，虽然均能使系统动态响应加快，但由于数字控制器存在采样和计算延时，导致逆变器控制实时性较差。虽然采用状态观测器后能够对延时进行补偿，但系统仍难以突破稳态下高控制精度的瓶颈［2-4］。特别是在非线性负载条件下，逆变器受到周期性负载电流扰动，导致输出电压波形出现严重畸变。为改善逆变器稳态特性，文献［1］提出了基于内模原理的重复控制，通过对波形误差的逐点补偿，实现高精度的稳态输出。但重复控制在得到输入指令后，控制信号会滞后一个参考周期输出，动态响应较差［5-7］。且传统重复控制补偿器常采用二阶低通滤波器，存在通带增益小、相位延迟等缺陷，需要再加入陷波器和相位补偿环节，导致设计过程复杂化［8-9］。

为满足逆变器输出兼具动态响应快和稳态精度高的要求，本文提出一种基于电流观测与重复控制的逆变器多环控制策略。该策略中内层控制器采用输出电压和电容电流反馈控制，建立电流观测器对电容电流进行观测，使逆变器具有快速动态响应。在内层控制器的基础上设计了外层改进型重复控制器，并将FIR 数字滤波技术引入重复控制，提高了系统稳态控制精度的同时大大简化了控制器设计过程。

1 逆变器数学模型

SPWM单相电压型逆变器拓扑结构见图1。

图1 SPWM单相电压型逆变器拓扑结构图Fig.1 Topology of SPWM single-phase voltage source inverter

图1 中Udc为直流侧电压，vtri为角载波的幅值。假设逆变器所带负载为纯阻性负载并且其开关频率远高于调制信号vcon的频率。根据KVL和KCL定律建立的该电路拓扑平均连续时间模型为

式中：Kpwm=Udc/vtri。

G0（s）为纯阻性负载情况下，从vcon到uo的传递函数如下式所示：

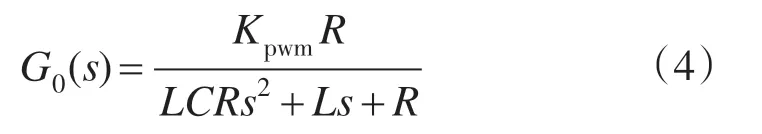
由式（4）可知，开环逆变器是一个二阶欠阻尼系统，扰动抑制能力很弱，系统稳定性较差。为此，本文首先设计内层双环控制器，以使系统稳定性和动态响应得到改善。

2 双闭环控制器的设计

由于逆变系统中产生负载扰动时滤波电感电流不会发生突变，但滤波电容电流却能及时反映负载变化，因此采用电容电流反馈能够提高系统的动态响应速度。且采用电容电流反馈可以将负载扰动Id包含在反馈环路的前向通道内，这样在发生负载扰动电流变化时控制系统能将Id及时地前馈到双闭环控制器，控制器进行相应的调节作用，及时地对扰动产生抑制，有效增强系统稳定性。

数字控制中存在着采样延时和算法延时，严重影响系统的控制精度和响应速度［10-11］。为了消除由采样、A/D 转换以及控制算法执行时间所造成的控制延迟，本文建立了电容电流观测器。电容电流观测器能够通过采样所得的电容电流值预测出标准的电容电流值，从而补偿延迟，使系统获得更快的动态响应速度，具体设计过程如下。

内环电容电流采样时序示意图如图2 所示。Ts为采样周期，Td为采样延时时间。采样点为ic（n），2 个标准采样点之间的点表示为ic（n，m）。其中，m 是延迟时间系数，延迟时间Td可表示为（1-m）Ts。则Td=0时可得m=1，Td=Ts时可得m=0。利用z 变换进行内环设计［11］，F（s）为采样延时，在时域下采样时间延迟Td可以表示为e-Tds；PWM逆变器可表示为零阶保持器H(s)=(1-e-Tis)/s 和比例调节器K的组合，这里K=KPWM。电流环开环传递函数为

图2 内环电容电流采样时序示意图Fig.2 Sampling period schematic of inner loop capacitor current

对式（5）进行z 变换：

根据式（6）可以得到如下方程：

根据式（7）建立状态观测器：

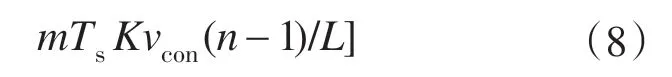
其中k=KTsD(z)/L，D(z)表示电流环控制器，将上式用z 变换表示：

其特征方程为

当k=1 时，即当D(z)=L/KTs时，电流内环就可实现最小拍电流控制。由上式可知，最小拍控制器实际上仅仅是一个比例环节，整个内环实现的控制策略相当简单，系统可以采用较高的电流采样频率，以实现更高的观测精度。

由于电流内环采用电容电流反馈，负载的扰动电流被包含在电流内环的内部，从而电流内环对负载扰动有着较强的抑制作用，保证了系统的稳定性。因此在设计电压外环时仅需考虑电压控制器输出响应的快速性，故电压环控制器E(z)采用比例环节即可，比例系数为Kp。双闭环控制系统结构框图见图3。

图3 双闭环控制系统结构框图Fig.3 Block diagram of the dual-loop control system

3 重复控制器的设计

为了解决双环控制逆变器在非线性负载下输出电压波形发生畸变的问题，实现输出电压对正弦参考信号的无静差跟踪，提高系统的抗负载扰动能力。本文在双环控制器的基础上增加了改进型重复控制器，改进型重复控制能够逐周期地对控制误差进行补偿，在任何负载情况下均可实现无静差控制。重复控制器结构如图4所示。其中P(z)为上一节中设计的双闭环控制系统；Q(z)和C(z)分别为重复控制辅助补偿器和针对受控对象的补偿器，C(z)=krzkS(z)；d(z)为周期性扰动。

图4 重复控制器结构框图Fig.4 Block diagram of the repetitive control system

由图4可见，误差信号e(z)与参考信号Uref(z)、扰动信号d(z)的关系为

由上式可得系统特征方程：

欲使系统稳定，特征方程特征根的模应小于1。

令 J(z)=Q(z)-krzkS(z)P(z)

只要满足下式则系统稳定，

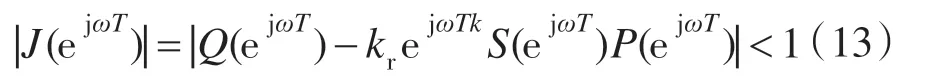
式中：T为采样时间；ω ∈(0,π/T)。

对于理想重复控制器有Q（ejωT）=1，这表示当Q(z)=1 时重复控制在任意周期扰动下均可实现无静差跟踪给定参考信号［12-13］。随着频率升高C(z)=krzkS(z)的轨迹向左移动，高频段时J(z)的轨迹可能会在单位圆上或外部，此时系统处于临界稳定或不稳定状态。针对此问题Q(z)常取小于1 的常数，使原点为Q(z)的单位圆左移，从而保证系统在全频段内稳定，本文根据经验值取Q(z)=0.95。

补偿器S(z)对系统稳定性起着决定性作用，传统重复控制器中S(z)常采用二阶低通滤波器，由于其存在着通带增益损失大、阻带衰减率低、引起附加相移等缺陷，因此不得不在控制器中引入陷波器和相位补偿环节，这就导致设计问题复杂化。为了简化设计过程，本文将FIR 数字滤波器引入到重复控制器设计之中。由数字信号理论可知，FIR 低通滤波器具有低频段零增益、频率选择性好、谐振峰处及高频段衰减率高等优点，满足补偿器S(z)的性能要求［14］。本文在Matlab软件环境下使用Kaiser窗函数法进行FIR低通滤波器设计。首先根据逆变器模型确定对应FIR 滤波器具体参数，这是其设计过程中的关键环节，这些参数直接影响补偿器的幅度和相位频率响应特性。FIR 滤波器具体参数确定如下：采样频率为18 kHz，通带范围为0～500 Hz，通带增益波动小于1 dB，阻带范围大于800 Hz，阻带增益小于-40 dB。运行滤波器设计程序，得到相应的滤波器单位脉冲响应参数h（n）如表1所示。

表1 FIR滤波器单位脉冲响应参数h（n）Tab.1 Parameters h(n)of FIR filter impulse response

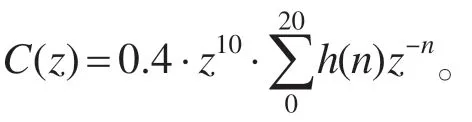
图5示出双环控制逆变器加入重复控制前后P(z)和C(z)P(z)的波特图，其中虚线和实线分别代表P(z)和C(z)P(z)。从图5 中可以看出，在内层双环控制作用下，逆变器开环幅频特性谐振峰值处削减了20 dB，但是高频段的衰减率仍然仅有-10 dB/dec。而在加入重复控制之后，采用零相移FIR低通滤波器构造的补偿器不仅保持了双环控制逆变器中低频段零增益、零相移的特性，且大大提高了高频衰减率，衰减率达到-60 dB/dec，使得高频段的增益幅值仅有-50～-120 dB，因此高频段的控制误差可以忽略，从而系统在全频段内均具有良好的稳定性。

图5 P(z)和C(z)P(z)波特图Fig.5 Bode diagram of P(z)and C(z)P(z)

4 实验研究

为验证所提出控制策略的正确性，本文在基于ARM STM32F103VB 控制的单相全桥逆变器实验平台上进行了实验验证。单相全桥PWM逆变器的相关参数为：输入直流电压Udc=250 V，输出交流有效值Uo=110 V，输出交流频率f=50 Hz，输出功率P=2 kW，开关频率fs=18 kHz，滤波电感L=1.5 mH，滤波电容C=20 μF，整流性负载电容Co=3 300 μF，整流性负载电阻Ro=25 Ω，功率器件IPM PM75RL1A120。

双环控制逆变器带整流性负载的输出电压和电流波形如图6a所示。可以看出，双环控制对整流性负载电流扰动的补偿效果有限，波形产生了明显的畸变，输出电压的THD 达到4.6%。本文所设计的多环控制逆变器带相同整流性负载时的稳态波形如图6b 所示，对比图6a 和图6b 可以看出加入重复控制后能够有效地提高系统稳态特性和改善输出电压波形，输出电压THD含量降低到1.4%。

图6 输出电压、电流波形Fig.6 Output waveforms of voltage and current

采用多环控制和纯重复控制逆变器在输出电压峰值处突增10 Ω阻性负载的动态特性波形分别如图7a 和图7b 所示。从图7a 可以看出，多环控制下逆变器在突增负载后输出波形在1 ms内就恢复了，且电压幅值不会有明显跌落，系统很快就能达到新稳态。重复控制虽然能够对误差进行逐周期补偿，但其在负载突增后一个周期内系统近似于开环，无法产生控制作用。从图7b能够看出突增负载后输出电压峰值存在明显跌落，且系统达到稳态时间较长。对比两种控制策略，可见多环控制器能够有效地改善重复控制的动态性能，提高动态响应速度。

图7 动态波形Fig.7 Transient waveforms

5 结论

结合已有逆变器控制策略存在的缺点，指出单一控制策略无法同时满足逆变系统对于动态响应速度、稳态跟踪精度及稳定性要求的问题，提出采用多环控制策略的解决方案。本文以电流观测和改进型重复控制为主要研究对象，从理论角度分析了方案的正确性，设计了双闭环控制器及重复控制器的具体参数，最后通过实验验证了方案的可行性，并从中总结出以下结论。

1）双闭环控制器采用电容电流反馈不仅能够及时感应到输出电流的变化情况，而且能够有效地抑制负载扰动，使逆变器具备良好动态响应速度、系统稳定性和抗负载扰动能力。

2）采用零相移FIR 低通滤波器作为重复控制补偿器，大大简化了重复控制器的设计过程，提高了逆变系统在严苛负载条件下的稳态控制精度和波形正弦度，减小了跟踪误差和谐波畸变率。

3）基于电流观测与改进型重复控制的逆变器多环控制策略，兼具动态响应快、稳态精度高、抗负载扰动能力强等优点，满足高性能电压输出控制场合的要求。

［1］ Tzou Ying-Yu，Rong Shyang，Jang Shih-Liang，et al.Highperformance Programmable AC Power Source with Low Harmonic Distortion Using DSP-based Repetitive Control Technique［J］.IEEE Trans.on Power Electronics，1997，12（4）：715-725.

［2］ Jiang Shuai，Cao Dong，Li Yuan et al.Low-THD，Fast-transient，and Cost-effective Synchronous-frame Repetitive Controller for Three-phase UPS Inverters［J］.IEEE Trans.on Power Electronics，2012，27（6）：2994-3005.

［3］ Escobar G，Valdez A A，Leyva-ramos J，et al.Repetitive-based Controller for a UPS Inverter to Compensate Unbalance and Harmonic Distortion［J］.IEEE Trans.on Industrial Electronics，2012，54（1）：504-510.

［4］ 梅红明，刘建政.基于电流观测器的三相变流器重复控制方法［J］.中国电机工程学报，2011，31（27）：59-65.

［5］ 宋建成，刘国瑞，李永军，等.基于改进重复控制和双闭环PI 控 制 的 逆 变 器 研 究［J］.煤 炭 学 报，2011，36（10）：1768-1772.

［6］ 杨豪，赵军红，朱雁南，等.谐波补偿重复控制及其在逆变器控制中的应用［J］.电气传动，2013，43（8）：44-48.

［7］ 曾晓生，杨苹，林旭成.重复和PI复合控制在光伏逆变器中的应用［J］.电气传动，2012，42（8）：47-49.

［8］ 张凯，彭力，熊健.基于状态反馈与重复控制的逆变器控制技术［J］.中国电机工程学报，2006，26（10）：56-62.

［9］ 郭伟玮，卢晓东，冯仁剑.一种快速重复控制策略在单相逆变电源中的应用［J］.电气传动，2013，43（9）：56-59.

［10］郭卫农，陈坚.基于状态观测器的逆变器数字双环控制技术研究［J］.中国电机工程学报，2002，22（9）：64-68.

［11］郭卫农.CVCF 电压型逆变器输出波形瞬时控制技术研究［D］.武汉：华中科技大学，2001.

［12］Zhang Bin，Wang Dan-wei.Linear Phase Lead Compensa tion Repetitive Control of a CVCF PWM Inverter［J］.IEEE Trans.on Industrial Electronics，2008，55（4）：1595-1602.

［13］Chen S，Lai Y M.Analysis and Design of Repetitive Controller for Harmonic Elimination in PWM Voltage Source Inverter Systems［J］.IET Power Electronics，2008，1（4）：497-506.

［14］赵光宙.信号分析与处理［M］.北京：机械工业出版社，2006.