基于ADRC及变结构PID控制的伺服系统研究

吴向阳，毕世华，张连广，朱政，巫伟男

（1.北京理工大学宇航学院，北京100081；2.北京特种机械研究所，北京100143；3.第二炮兵驻北京地区军事代表室，北京100143）

目前，发射车全电驱动已成为未来发展方向，其中导弹发射箱的电动起竖为关键技术。为使电驱动具有较好使用性能，电机驱动系统应具有足够大的启动转矩及较大的调速范围。

永磁同步电机交流伺服系统在全电驱动发射车中需求非常广泛，是目前的热点研究领域之一。发射车导弹起竖过程中载荷变化剧烈，伺服系统必须对起竖过程中的未知扰动具有很强的鲁棒性。在控制策略方面，以PID 控制为代表的经典控制策略已经在PMSM 中获得了广泛应用。但PID 调节器仍然是线性控制器，抗干扰性能力不强，在导弹起竖载荷变化剧烈时效果较差。目前对于PMSM 的控制策略的研究还集中在鲁棒控制［1］、自适应控制［2］、变结构控制［3］。但由于PMSM 系统是一个多变量、非线性、强耦合的复杂系统，很难用精确的数学模型来描述，就使得这些基于精确数学模型的控制理论显示出一定的局限性。基于遗传算法和神经网络［4］的控制策略不依赖于对象模型，对未知扰动具有较强鲁棒性，但实现非常复杂，应用困难。

自抗扰控制技术［5］是中国科学院韩京清教授近年来提出的一种非线性鲁棒控制技术。该控制技术算法简单，适用于数字化设备，且具有超调小、响应快、精度高、抗干扰能力强等特点，对系统不确定和外扰动具有很强的鲁棒性［6］。到目前为止，自抗扰控制器已经在许多复杂的非线性控制问题中得到了深入研究，如飞行器控制、电机控制、机械手控制、非圆滑齿轮控制、励磁发电控制、运动控制、陀螺仪平衡控制、惯导系统初始对准、楼宇结构控制、火力发电控制、倒立摆控制等［7-10］。本文将进一步研究交流伺服系统控制问题，提出一种基于ADRC 及变结构PID 控制的永磁同步电机伺服系统。通过ADRC 设计速度环控制器，利用ESO对系统不确定因素进行观测并加以补偿，使得伺服系统对参数摄动及外部扰动具有较强的鲁棒性；同时利用变结构PID 设计位置环控制器，实现了“小误差大增益，大误差小增益”的非线性控制，提高系统响应速度。

1 交流伺服系统控制问题描述

交流伺服系统主要由伺服控制器、驱动电路、伺服电动机及相应反馈检测器件组成，常采用电流环、速度环、位置环的3 闭环系统，如图1所示。电流控制器的参考输入是经过速度控制器调节后的电流，其作用是提高系统的快速性，抑制电流波动，保障系统安全运行。速度控制器的参考输入为位置控制器调节后的控制量，其作用是增强系统抗负载扰动能力，抑制速度波动。位置控制器的参考输入为位置指令信号，作用是保证系统稳态精度和动态跟踪性能。图1 中Gp(s)为位置调节器，Gs(s)为速度调节器，Gi(s)为电流调节器，L 为电机电感，Rs为电枢电阻，J为电机转动惯量，JL为负载转动惯量，Kt为电机转矩系数，Ke为电机反电势系数，θ 为电机转角，ω 为永磁同步电机的角速度，iq为电机q轴电流，θ*为给定电机转角，ω*为给定角速度，iq*为给定电流，fτ为黏性摩擦力矩比例系数，Tf为摩擦干扰力矩，TL为负载转矩，Te为外部扰动转矩。

图1 伺服系统框图Fig.1 The block diagram of servo system

伺服系统控制的目的就是在系统存在参数不确定、外部扰动及非线性因素的情况下实现给定信号的跟踪控制，可由下式表述：

本文只考虑速度环及位置环设计，电流环采用传统PI控制方式，不作深入研究。

2 基于ADRC的速度环控制器设计

ADRC 是不依赖被控对象模型，因此设计时不需要考虑系统的线性或非线性、时变或时不变等特性。对于可以化为“积分串联型”对象，可以设计二阶ADRC 控制器进行控制。可由下式表示：

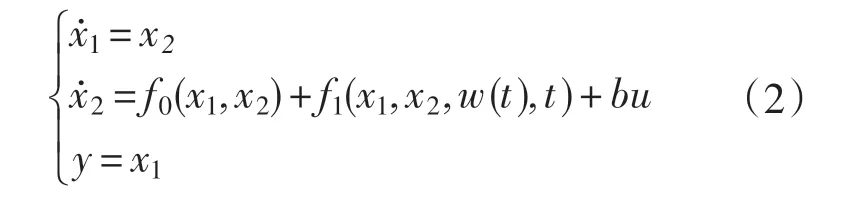
式中：x1，x2为系统的状态变量；f0(x1,x2)为系统已知函数；f1(x1,x2,w(t),t)为系统未知函数（包括参数不确定、内部扰动、外部扰动等不确定因素）；b 为系统控制量增益；u 为系统控制量。

二阶ADRC 结构如图2 所示，由跟踪微分器（TD）、扩张状态观测器（ESO）、非线性反馈控制律（NLSEF）3 部分组成。TD 为参考输入安排过渡过程，减小系统的初始误差，解决系统响应快速性和超调性之间的矛盾；ESO的输出是系统状态的估计值，是系统的内外扰动总和的估计值；非线性反馈控制律用来给定控制信号，该控制信号中含有扰动量的补偿分量。

图2 ADRC控制框图Fig.2 The block diagram of ADRC control

二阶ADRC中的跟踪微分器、扩张状态观测器、非线性反馈控制律算法如下。

2.1 跟踪微分器

式中：v1为给定速度ω*的跟踪信号；v2为给定速度ω*的微分信号；r 为速度因子；h0为滤波因子。

fhan(v1-v,v2,r,h0)的推导如下：

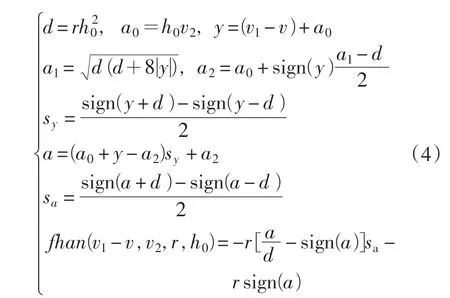
2.2 扩张状态观测器

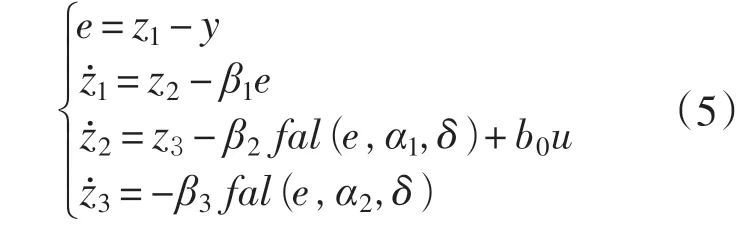
式中：y 为电机转速输出ω；z1为转速ω 的跟踪信号；z2为z1的微分信号；z3为总扰动的跟踪信号；e 为误差信号；β1，β2，β3为控制器可调参数；α1，α2满足0 ＜α1＜1 ＜α2；δ 满足δ ＞0。

函数fal(e,α,δ)定义为

2.3 非线性反馈控制律

式中：k1，k2为可调控制增益；b0为控制增益b的估计值。

3 基于变结构PID 的位置环控制器设计

伺服系统位置环控制关系到整个系统的响应速度及跟踪精度，因此其设计极为重要。如果采用传统的PID 控制方式，大角度响应速度和小角度的响应速度不能同时满足，并且在非线性瞬态扰动下系统很难保持稳定性。因此，位置环控制采用如下变结构PID控制方式：

式中：Ks＞1；Gi(e)为误差e(t)的减函数，0 ＜Gi(e)≤1；Gd(e)为误差e(t)的增函数，0 ＜Gd(e)≤1。

该控制方式在|e(t)|≥EA误差较大阶段采用P 控制，快速响应的同时避免了积分饱和对系统的影响。在EB≤ |e(t)|＜EA的中间过程采用PD控制模式，快速响应的同时利用微分环节减小系统超调；在小偏差段 |e(t)|＜EB，随着误差e(t)的减小，积分作用逐渐增强，微分作用逐渐减小，可以有效消除稳态偏差。同时采用较大的比例、积分和微分系数，利用小误差大增益的控制方式，改善小角度的响应效果。

4 实验验证

为验证本文控制算法的有效性，利用交流伺服实验平台，进行带载运行测试，加入外部扰动力矩，验证该控制算法在速度控制时的鲁棒性及位置控制时小角度的快速响应特性，实验平台原理框图见图3。

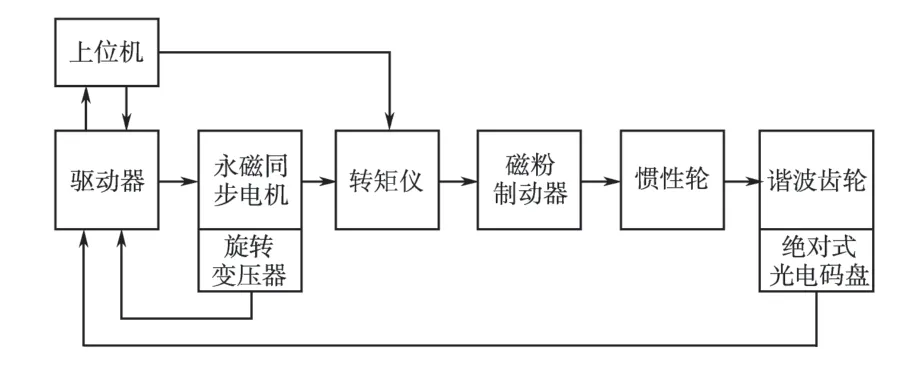
图3 实验平台框图Fig.3 The block diagram of experiment platform

4.1 速度控制

考虑带有摩擦扰动力矩的速度控制，分别在ADRC 控制及传统PID 控制时加入外部扰动，验证控制算法式（7）的动态特性，其中给定速度ω*=200 r/min。

图4为ADRC控制系统加入外部扰动力矩的速度响应曲线。图5为ADRC控制加入扰动后的转矩曲线。图6为传统PID控制系统加入外部扰动力矩的速度响应曲线，其中加载在系统轴上的转矩见图5，图7。

图4 ADRC加入扰动后的速度响应Fig.4 The speed response of ADRC control with disturbance

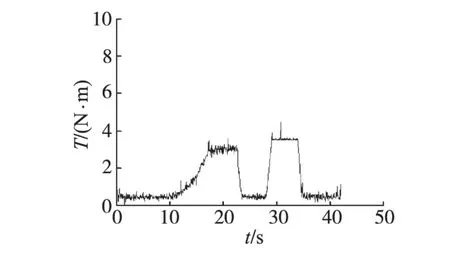
图5 ADRC控制加入扰动后的转矩曲线Fig.5 The torque response of ADRC with disturbance

图6 传统PID加入扰动后的速度响应Fig.6 The speed response of PID control with disturbance

图7 传统PID控制加入扰动后的转矩曲线Fig.7 The torque response of PID control with disturbance

可以看出ADRC 控制策略能够无超调且准确快速地跟踪给定速度，对外部扰动具有良好的鲁棒性。PID 控制策略虽然也具有良好的鲁棒性，但超调较大且在扰动加入时动态性能较差。

4.2 位置控制

为验证伺服系统的位置跟踪性能及小角度时的响应能力，设置给定位置θ*=80°（θ*为经过谐波齿轮后的负载角度），同时位置跟踪过程中加入扰动力矩。

图8a为变结构PID控制系统的位置响应曲线，图8b为传统PID控制系统的位置响应曲线。可以看出变结构PID控制策略在小角度阶段有良好的快速性。传统PID控制策略虽然也能有效跟踪给定位置，但在小角度响应时较慢，响应时间较长。

图8 加入扰动后位置响应Fig.8 The position response with disturbance

5 结论

本文将自抗扰控制技术应用于永磁同步电动机伺服系统中，设计了基于自抗扰控制器及变结构PID 控制器的PMSM 位置伺服系统。该控制器不依赖被控对象模型，通过ESO 对系统不确定进行观测并在控制器中给予补偿，因此该控制算法对系统参数变化及外部扰动具有很强的鲁棒性。实验结果验证了该控制策略的有效性。

［1］ Lin F J.A Robust PM Synchronous Motor Drive with Adaptive Uncertainty Observer［J］.IEEE Transactions on Energy Control，1999，14（4）：989-995.

［2］ Tan K K，Huang S N，Lee T H.Robust Adaptive Numerical Compensation for Friction and Force Ripple in Permanentmagnet Linear Motors［J］.IEEE Transactions on Magnetics，2002，38（1）：221-228.

［3］ Yan Z，Jin C，Utkin V I.Sensorless Sliding-mode Control of Induction Motors［J］.IEEE Transactions on Industrial Electronics，2000，47（1）：286-297.

［4］ Theocharis J，Petridis V.Neural Network Observer for Induction Motor Control［J］.IEEE Control System Magazine，1994，6（2）：101-112.

［5］ Han J Q.From PID to Active Disturbance Rejection Control［J］.IEEE Transactions on Industrial Electronics，2009，56（3）：900-906.

［6］ Sun D.Comments on Active Disturbance Rejection Control［J］.IEEE Transactions on Industrial Electronics，2007，54（6）：3428-3429.

［7］ Xia Yuanqing，Zhu Zheng，Fu Mengyin.Back-stepping Sliding Mode Control for Missile Systems Based on Extended State Observer［J］.IET Control Theory Applications，2011，5（1）：93-102.

［8］ Su Y X，Zheng C H，Yang D.Automatic Disturbances Rejection Controller for Precise Motion Control of Permanent Magnet Synchronous Motor［J］.IEEE Transactions on Industrial Electronics，2005，52（3）：133-139.

［9］ Su J，Qiu W，Ma H，et al.Calibration-free Robotic Eye-hand Coordination Based on an Auto Disturbance-rejection Controller［J］.IEEE Transactions on Robotics，2004，20（5）：899-907.

［10］Wu D，Chen K，Wang X.Tracking Control and Active Distur-Bance Rejection with Application to Noncircular Machining［J］.International Journal of Machine Tools and Manufacture，2007，47（5）：2207-2217.