十字形液晶分子混合物系统的相变
2015-06-10朱玲玲
朱玲玲,刘 红
(南京师范大学 物理科学与技术学院,江苏 南京 210023)
十字形液晶分子混合物系统的相变
朱玲玲,刘 红*
(南京师范大学 物理科学与技术学院,江苏 南京 210023)
研究了由2种十字形液晶分子构成的混合物系统。假设分子间的简单相互作用,运用平均场理论,得到混合物液晶在分子结构参数rA(A类液晶分子短、长棒比)和约化温度t平面内的相图。结果表明,相图存在一Landau点,系统经此点由各向同性相可直接进入双轴向列相。此点所对应的优化分子结构与A,B类分子结构、混合比有关。按等比例混合的棒状、圆盘状液晶分子系统即具有此优化分子结构。随着B类液晶分子短、长棒的比值rB增加,Landau点处的rA减少。对比混合物系统和相分离系统的自由能曲线,发现增加异种液晶分子间的相互作用强度,升高温度,缩小异种分子间的形状差异可使系统不发生相分离。
混合物;双轴向列相;相变
1 引 言
双轴向列相液晶的相变一直是液晶理论和实验研究的课题。近年来由于小分子热致双轴向列相的发现,以及其在显示方面的潜在应用价值,使得人们对双轴向列相液晶的相变研究产生新的兴趣。
理论上,1970年Freiser[1]利用一具有旋转不变性的分子相互作用能,在平均场近似下,得到系统自由能为序参数的函数,指出在平衡态下双轴向列相出现的可能。在实验上,1980年Yu 和 Saupe[2]在由钾、十二酸酯-1正癸醇构成溶致液晶系统中,通过小范围的变化温度和浓度,第一次测得双轴向列相的存在。在热致液晶系统中,想要得到双轴向列相比较困难。经过二十多年的寻找,小分子热致液晶中的双轴相才被证实。Acharya[3]在由刚性弯曲核分子[4](或V形分子)构成的热致液晶中测出其独特的X射线衍射图案, 结果清晰地展示出系统的双轴相。Madsen[5]等利用氘核磁共振在带有永久偶极矩的V形液晶分子系统中也明确测出双轴相。2006年Neupane[6]等在由弹性键连接的四足形液晶分子系统中运用光的动态散射也测出了双轴相。
在弯曲核分子系统中,产生双轴相的主要原因是由于分子含有较强的电偶极矩;在四足形分子系统中,由于弹性键的存在使分子短轴转动受限,系统容易出现双轴相。传统上,能产生双轴向列相液晶的分子模型,除了上述分子以外,还有棒状和盘状液晶分子相混合的系统[7]。但在这种液晶系统中,相不稳定性一直是关键问题。以往的研究显示,混合物液晶中的双轴相有可能分离成两种单轴相,其中一部分主要由棒状液晶分子构成,另一部分主要由盘状分子构成[8-9]。2002年,Szabolcs Varga等[10]运用Onsager理论研究了棒盘状混合物液晶系统的相变,讨论了异种液晶分子相互排斥作用强度与相稳定的关系。为避免相分离的出现,Alejandro Cuetos[11]等使用Monte Carlo模拟,对异种分子间的相互作用引进了一吸引势,从而得到稳定的双轴相。Torsten Hegmann[12]等在实验上采用2种液晶分子(均可抽象为矩形板)的混合物,其异种液晶分子间相互作用不同于同种分子间相互作用,它们之间具有面-面相互吸引的作用,这使得矩形板的短轴转动自由度受到限制,系统被测出双轴近晶A相,这表明存在着异种分子相互作用不同于同种分子相互作用的混合物系统。为进一步研究混合物液晶系统中双轴相的稳定性问题与相互作用势的关系,本研究考虑两种矩形板液晶分子构成的混合物,将其抽象为十字形分子。假设同种和异种液晶相互作用强度彼此独立,利用平均场理论,研究平衡态时双轴相序参数与相互作用强度,分子结构,成分比等的关系,并讨论当异种分子间相互作用强度不同时,系统在何种参数范围内会出现稳定的双轴相。
2 理论推导
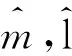

图1 十字形液晶分子结构示意图Fig.1 A schematic diagram of cross-like molecules
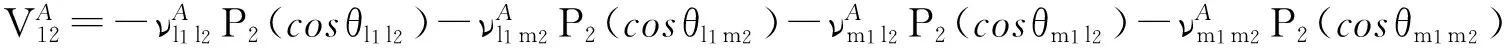
(1)
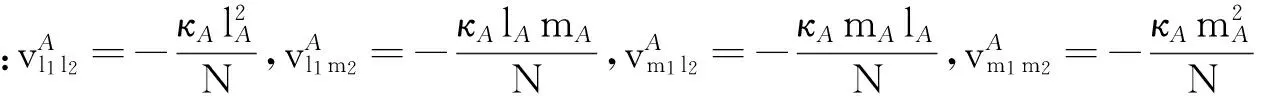

(2)



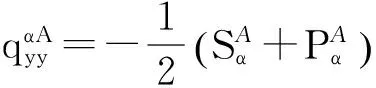

类似地,可得A类分子1在所有B类液晶分子所产生的平均场中的能量为

(3)
由此,A类任意分子i在总平均场中的能量为:

(4)


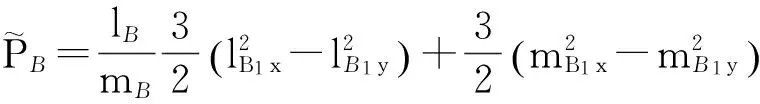
(5)


同理可得B类任意分子i在总平均场中的能量为
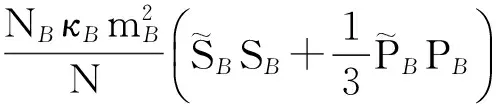
(6)
混合物液晶系统的内能为

(7)
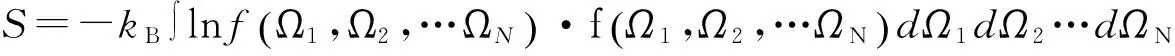
故对于混合物系统,熵可写为
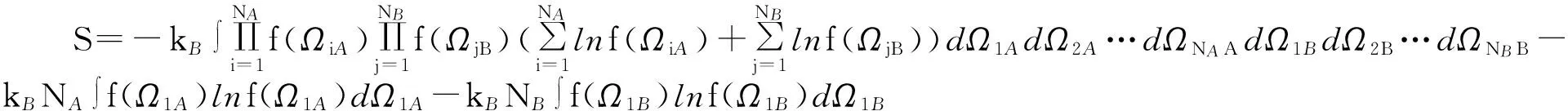
(8)
将(7),(8)中内能和熵表达式代入自由能F=U-TS中,得到系统的自由能为:
kBT(NAlnZA+NBlnZB).
(9)
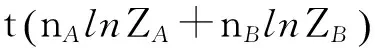
(10)
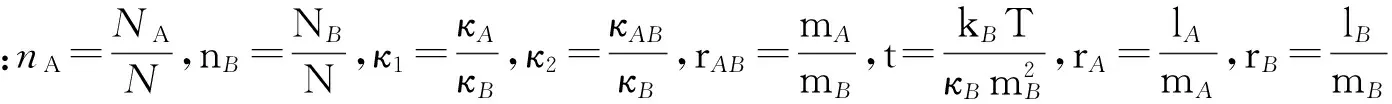
当系统处于平衡态时,自由能有极小值。将f对序参数求极值,即

(11)
得到系统序参数所满足的自洽方程:
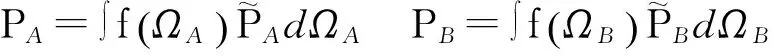
(12)

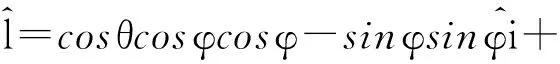
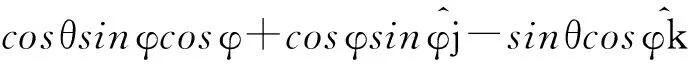
(13)
其中:θ,φ,ψ为欧拉角,因此dΩ=sinθdθdφdψ。将(13)代入(12)中,求其数值解,可得到序参数SA、PA、SB、PB随温度,分子结构参数,相互作用强度之间的关系,由此讨论系统的相变。
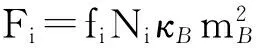
t(nAilnZAi+nBilnZBi) ,
(14)
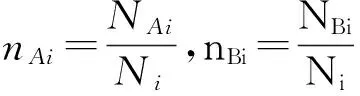
当子系统处于平衡态时,将fi对序参数求极值可得
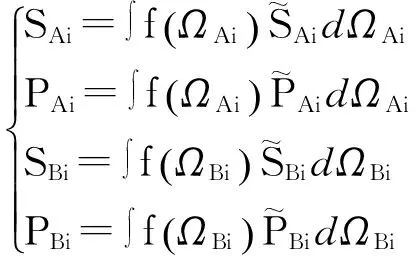
(15)
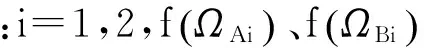
对式(15)给出的系统八个序参数所满足的方程求数值解,可得两个子系统序参数随温度等参数的变化关系和平衡态下的自由能密度。
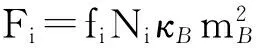
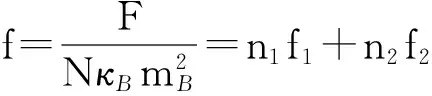
(16)
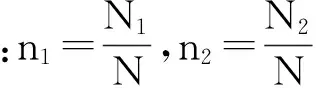
3 结果讨论
3.1 混合物系统的相变
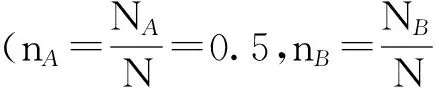


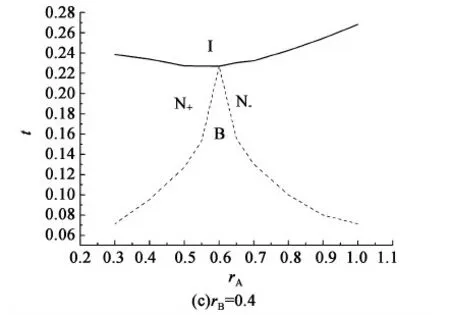
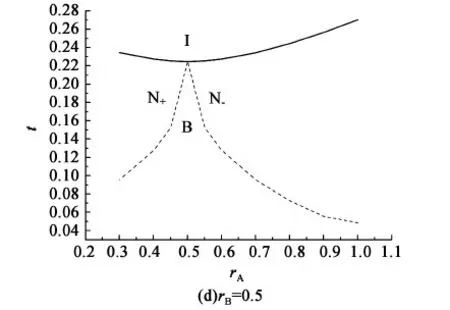

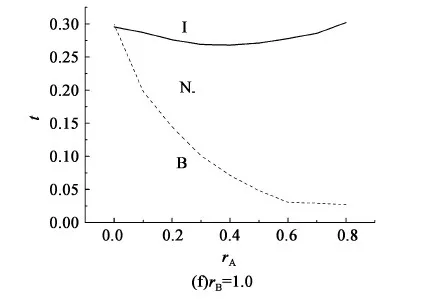
图2 系统在A类分子结构参数rA和温度t平面内的相图Fig.2 Phase diagrams in the plane of A type molecular structure parameter rA and temperature t
为分析相变过程,图3给出当rB=0时(B类分子为棒状分子),在Landau点rA=1.0(A类分子为圆盘状分子)处A,B两类液晶分子序参数随温度的变化曲线,其中qla,qma,qlb,qmb分别表示A、B类液晶分子的l,m棒的序参数矩阵,其矩阵的对角化矩阵元为qαixx,qαiyy,qαizz,α=l,m,i=a,b。该图显示当温度t≥0.3时,各序参数为零,混合物系统为各向同性相,当温度t<0.3,qmbzz>0,qmayy<0,qmazz>qmaxx,表明B类分子的m棒沿某一方向(如z轴)优先排列,A类分子的m棒沿垂直于y轴方向排列。A类分子m棒沿z轴的有序度大于沿x轴的有序度,产生出双轴相。这一双轴相是完全是由于棒状,圆盘状分子的相互作用所造成。仅由具有轴对称性的圆盘状分子,长棒状分子构成的单一系统是无法产生双轴相的。



图3 当rB=0,rA=1.0时序参数矩阵元随温度的变化Fig.3 Curves of order parameters as functions of temperature. rB=0,rA=1.0
3.2 相分离研究
上述相图的成立是基于系统不存在相分离。为分析系统的相分离问题,考虑由1,2两个子系统构成的总系统。式(18)给出此系统的自由能表达式为两子系统序参数的函数。对其求极值,可得平衡态下的自由能。将此值与完全混合系统平衡态下的自由能式(10)作比较,可以判断系统是否出现相分离。
图4给出了圆盘状(A类,rA=1.0)和棒状(B类,rB=0)两种液晶分子构成的系统自由能随温度的变化曲线图,其中M曲线表示完全混合系统(记为M系统)的自由能,DM曲线表示完全分离成圆盘状分子和棒状分子两个子系统时的总系统(记为DM系统)的自由能。在混合物系统M中,取κ1=1.0,rAB=1。在相分离系统DM中,取子系统1,2的分子数占总分子数的比分别为n1=0.5和n2=0.5。设系统1由圆盘状分子构成,即nA1=1.0,nB1=0.0,系统2由棒状分子构成,即nA2=0.0,nB2=1.0。
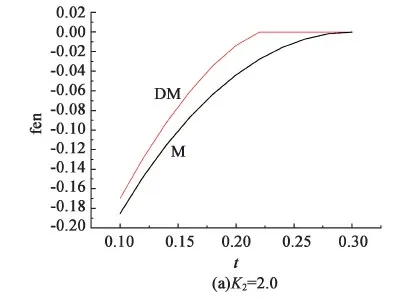
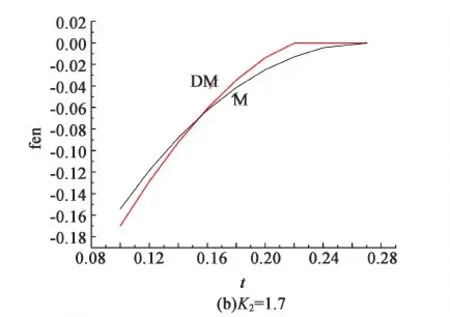

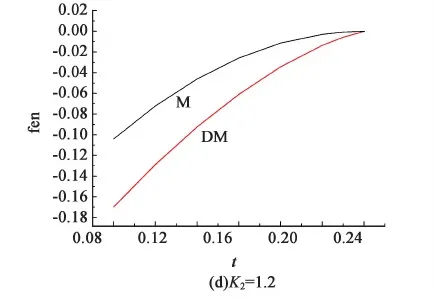
图4 当rA=1.0,rB=0,κ2变化时,混合物系统M和相分离系统DM自由能随温度的变化Fig.4 Curves of free energy of completely mixed system M and free energy of phase separated system as functions of temperature for different values of κ2. rA=1.0,rB=0.
在图(a)中,混合物系统M的异类分子间的相互作用强度为κ2=2.0,大于同种液晶分子间的相互作用强度κ1=1.0。由图知,当t<0.3时,系统M的自由能低于系统DM的自由能,系统处于异种分子间完全相互混合的状态。当t≥0.3时,系统处于各向同性相。在图(b)中,混合物系统M的κ2=1.7>κ1=1.0。当t<0.155时,系统DM的自由能低于系统M的自由能,系统处于异种分子间相分离的状态。在图(c)和图(d)中,混合物系统M的κ1=1.0,κ2分别为1.5和1.2。由图知,当t<0.198和t<0.220 2时,系统处于相分离态。这表明,随着异种分子间相互作用强度κ2减小,混合物系统M存在的温度范围逐渐减小,以至当κ2=1.2时,能量最低的系统为完全相分离的DM系统。此外曲线表明,随着温度的增加,M系统与DM系统在同一温度处的能量差减小,这表明温度的升高有助于两种分子的混合。
本文也计算了在rA=1.0,0.6,0.5,0.4,0.3,0.2,rB=0,κ2=1.2时,混合物系统M和相分离系统DM的自由能随温度的变化。结果表明,随着rA的减小, A类液晶分子形状逐渐接近于B类液晶分子,异种分子形状间的差异逐渐减小,系统M存在的温度范围逐渐增加。 当rA=1.0,在向列相液晶存在的温度范围内系统均为完全相分离态。当rA=0.2时,系统均为完全混合态。当两种分子形状完全一致,系统均处于混合态,不存在相分离。类似的,固定rA值,变化rB值,可以发现随着异种分子间形状差异的减小,系统不易出现相分离。以上结果表明,增加异种液晶分子间的相互作用强度,升高温度,缩小异种液晶分子间的形状差异,可使系统易处于混合态。
4 结 论
本文考虑由两种十字形液晶分子构成的混合物系统。假设分子间的简单相互作用,运用平均场理论,得到在给定rB(B类分子短、长棒比)值时,混合物液晶系统在分子结构参数rA(A类分子短、长棒比)和约化温度t平面内的相图。结果表明相图存在一Landau点,降低温度,系统可直接由各向同性相经Landau点进入双轴向列相。此点所对应的优化分子结构与A,B类分子结构,混合比有关。按等比例混合的棒状、圆盘状液晶分子系统即具有此优化分子结构。一般地,当B类分子短、长棒比rB增加,Landau点处的rA减少。当rA=rB=0.5,系统为单一种类的分子系统,Landau点出现在rA=rB=0.5。对比混合物系统和相分离系统的自由能,发现增加异种液晶分子间的相互作用强度,升高温度,缩小异种液晶分子间的形状差异可使系统不发生相分离。
[1] Freiser M J.Ordered states of a nematic liquid [J].Phys.Rev.Lett.,1970, 24(19):1041-1043.
[2] Yu L J, Saupe A. Observation of a biaxial nematic phase in potassium Laurate-1-Decanol-water mixtures [J].Phys.Rev.Lett., 1980, 45(12): 1000-1003.
[3] Acharya B R, Primak A, Kumar S. Biaxial nematic phase in Bent-Core thermotropic mesogens [J] .Phys.Rev.Lett., 2004, 92(14): 145506-1-4 .
[4] 杜琼,游红军,汪晓燕,等.弯曲型向列相液晶研究进展[J].液晶与显示,2011,26(6):719-726. Du Q, You H J, Wang X Y,etal. Progress of bent-core nematic liquid crystals [J].ChineseJournalofLiquidCrystalsandDisplays, 2011, 2616:719-726. (in Chinese)
[5] Madsen L A, Dingemans T J, Nakata M,etal. Thermotropic biaxial nematic liquid crystals [J].Phys.Rev.Lett., 2004,92(14): 145505-1-4. (in Chinese)
[6] Neupane K, Kang S W, Sharma S,etal. Dynamic light scattering study of biaxial ordering in a thermotropic liquid crystal [J].Phys.Rev.Lett., 2006,97(20): 207802-1-4.
[7] Stroobants A, Lekkerkerker H N W. Liquid crystal phase transitions in a solution of rod-like and disk-like particles [J].Chem.Phys., 1984,88(16) : 3669-3674.
[8] Varga S, Galindo A, Jackson G. New types of phase behavior in binary mixture of hard rod-like particles [J].Mol.Phys.,2003, 101(6):817-825.
[9] Galindo A, Haslam A J, Varga S,etal. The phase behavior of a binary mixture of rodlike and disclike mesogens: Monte Carlo simulation, theory, and experiment [J].Chem.Phys.,2003, 119(10): 5216-5225.
[10] Varga S, Galindo A, Jackson G. Ordering transitions, biaxiality, and demixing in the symmetric binary mixture of rod and plate molecules described with the onsager theory [J].PhysRevE,2002,66(1): 011707(1-16).
[11] Cuetos A, Galindo A, Jackson G. Thermotropic biaxial liquid crystalline phases in a mixture of attractive uniaxial rod and disk particles [J].Phys.Rev.Lett., 2008, 101(23):237802(1-4).
[12] Hegmann T, Kain J, Diele S,etal. Evidence for the existence of the McMillian phase in a binary system of a metallomesogen and 2,4,7-trinitrofluorenone [J].Angew.Chem.,Int.Ed,2001,40(5):887-890.
[13] De Gennes P G, Prost J.ThePhysicsofLiquidCrystal[M].Oxford: Clarendon Press,1993:19.
Phase transitions of binary mixtures of cross-like liquid crystal molecules
ZHU Ling-ling, LIU Hong*
(SchoolofPhysicsandTechnology,NanjingNormalUniversity,Nanjing210023,China)
A binary mixture of two different cross-like molecules is considered. Supposing a simple interaction model between molecules, and using mean field approximation, phase diagrams in the plane of molecular structure parameterrA(the length ratio of short and long rods of A type molecule) and reduced temperaturetare obtained. The results show there exists a Landau point, through which the binary mixture can enter directly from isotropic phase to biaxial nematic phase. The optimal molecular structure at this point depends on the structures, the number ratio of A and B type molecules. Mixing rod-like and plate-like molecules with equal numbers will lead to this optimal structure. WhenrB, the length ratio of short and long rods of B type molecules increases, therAvalue at Landau point decreases. Comparing the free energy curves corresponding to mixed system and phase separated system completely, it is found that by increasing the interaction strength between different types of molecules, increasing temperature, decreasing the structural difference between different molecules, the chance of phase separation will be reduced.
binary mixture; biaxial nematic; phase transition
2014-07-14;
2014-08-08.
江苏省科技厅项目(No.BK2009399)
1007-2780(2015)02-0194-08
O753+.2
A
10.3788/YJYXS20153002.0194
朱玲玲(1988-),女,安徽怀宁人,硕士,研究方向为液晶物理理论。E-mail:06028@njnu.edu.cn
*通信联系人,E-mail: 06028@njnu.edu.cn
