基于STL模型的轮廓线自适应分层方法研究
2015-06-09周惠群吴建军
周惠群,吴建军
(西北工业大学现代设计与集成制造技术教育部重点实验室,陕西西安 710072)
基于STL模型的轮廓线自适应分层方法研究
周惠群,吴建军
(西北工业大学现代设计与集成制造技术教育部重点实验室,陕西西安 710072)
0 引言
计算层片厚度是CAD模型分层的最重要的过程之一。它直接影响加工零件的质量、精度、性能以及整个快速成型全过程的效率[1-2]。在快速成型的发展里程中,国内外学者广泛地研究了层片厚度的计算方法[2-10]。在分析STL模型的传统分层方法的基础上,提出了一种针对该模型的自适应分层方法,该方法通过对STL模型的3条轮廓外形线的分段值进行加权来计算层片厚度。
1 目前的分层方法
在快速成型系统中,目前的分层方法主要分为基于STL模型的分层方法和基于CAD模型的直接分层方法,但由于历史等原因,目前的大多数快速成型系统仍采用基于STL模型的分层方法。针对三维模型的分层问题,参考文献[2]提出了基于三角面片位置信息的分层算法,参考文献[3- 4]提出了基于拓扑信息的切片算法,参考文献[5]等提出基于切片轮廓信息来确定层片厚度,这种方法对切片轮廓计算精度要求高,一般需多次计算切片轮廓,实际应用比较少。参考文献[6- 7]提出根据顶尖高度计算层片厚度,其后有多种文献采用了这种方法。参考文献[8]提出根据相邻两截面面积变化率计算层片厚度,参考文献 [9]等也采用了这种方法。该方法是通过比较相邻两层的面积差值来推测零件的表面几何特征的。与曲率算法相比,面积计算法的计算过程比较简单,但由于基准面积在不断变化,精度难以控制;另外,如果条件不满足,则会存在重复计算。参考文献[10]提出了基于三角形面片法向矢量的自适应分层算法,该算法需要计算三角形面片法向矢量,计算量大。而采用曲率计算法,该算法的关键在于取得各个给定点的曲率,然而,要求出曲面上任意给定点处的曲率是比较困难的,而且在一次分层中,需要求出很多点的曲率,这就造成了这种算法实现上的困难。此外,顶尖高度法计算层厚公式形式太多,其中曲率半径的计算比较困难。
2 轮廓外形线的分层方法
通过分析传统的STL模型分层方法的不足,提出了一种基于STL模型加权轮廓外形线的分层方法。该方法对切片厚度的选取采用自适应方法,切片时针对STL模型先按照该模型的轮廓求出3条均布的轮廓外形线,然后将这3条轮廓外形线分段再加权,反复进行对比和分析,进而求出最佳分层厚度值。
2.1 分层厚度的计算
由于分层厚度的计算是快速成型制造中的关键,为了解决目前分层方法存在的问题,提出在分层厚度的选择上采用自适应分层。也就是说,在Z轴方向上根据STL模型的轮廓表面形状自动地改变分层厚度,进而实现和满足零件表面精度的要求。
2.1.1 轮廓外形线的求法
首先,在CAD系统中构建完成三维CAD模型后,将其转化为STL模型。然后采用CAD系统的剖切功能Section创建3条轮廓外形线。
具体的做法如图1所示,图1a是CAD模型的色调图,图1b所示的L1,L2,L3是STL模型的3条侧面轮廓外形线。它们是用3个过Z轴的平面P与STL模型的侧面相交得到的,这3条轮廓外形线作为考虑切片厚度的模型轮廓线。用3条外形线作为STL模型轮廓线主要是为了更全面地表示模型的侧面轮廓特征。注意在选取P平面时要尽量使求出的轮廓线能够反映出STL模型在Z轴方向的变化特征,而且这3条轮廓线的间距一般应该均布,当然也可以根据实际情况不均布。同时,还可以将其中1条移位,这时其他2条也跟着移位。因为目前计算机的速度很快,可以在不同的位置计算轮廓外形线,再将其反复对比和分析进而得出该轮廓外形线的最优值。
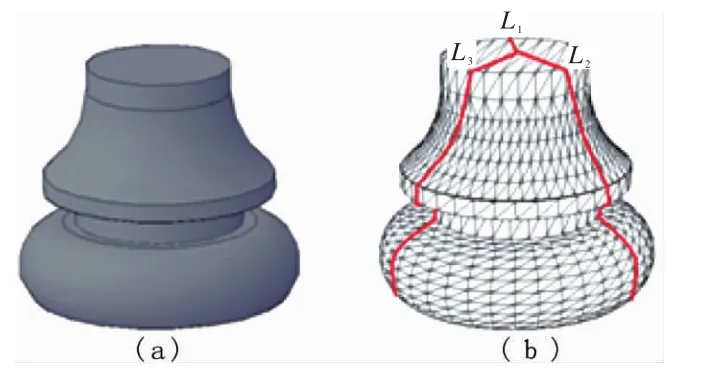
图1 CAD模型及STL模型的轮廓外形线
2.1.2 分层厚度的计算
分层厚度的计算过程是,如果STL模型的3条轮廓外形线中,不管哪一条中有一段是铅垂线段,则该线段部分按等层厚的分层方法处理。关键问题是轮廓外形线的斜线部分,依据2.1.1节求出的3条侧面轮廓外形线来计算切片厚度。在此过程中,根据实际情况确定一个最大切片厚度Zmax,一个最小切片厚度Zmin。因为STL模型的轮廓外形线上各点是连续的,斜线和X轴正方向的夹角在不停地变化。因此,采用的方法是根据轮廓外形线中分段后的斜线和X轴正方向的夹角的大小来确定该层切片的切片厚度。
STL模型的分层轮廓外形线和X轴正向夹角如图2所示。
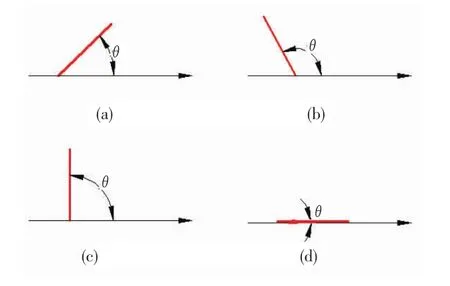
图2 轮廓外形线与X轴正向的夹角
从图2a、图2 b的观察过程可以得出结论,均匀切片时,当夹角在0o~90o之间时,夹角越大则轮廓面的台阶效应的越小,自适应切片算法中厚度应逐渐加大;当夹角在90o~180o之间时,夹角越大则轮廓面的台阶效应就越大,自适应切片算法中厚度应逐渐减小。根据数学中三角函数的关系,得出根据夹角求切片厚度的公式Z=Zmin+(Zmax-Zmin)×sinθ。
另外,在图2c中,轮廓外形线与X轴的正方向夹角为直角。若采用同样的厚度进行叠层,这种情况产生的面积偏移最小,不会出现CAD模型的轮廓台阶现象。所以自适应切片算法中,这种情况下可以取最大切片厚度Zmax。在图2d中,轮廓外形线与X轴正方向成0o或180o,此种情况如果在1条或2条轮廓外形线出现,则考虑第3条轮廓线的情况,这时可以单独计算第3条轮廓线的情况。若3条都是这种情况,则该情况完全可以不考虑,直接进入下一层的分层厚度计算。
在每次求厚度时,3条轮廓外形线上肯定是分别求得一个Z1,Z2,Z3值,那么切片的厚度一般可以取Z1,Z2,Z3这3个值的平均值Z。当然,取平均值是对于外形规则的零件而言(如回转体零件)的一种折衷的考虑。如果零件的外形不是规则的零件,那么多数情况下从3条轮廓外形线求得的Z1,Z2,Z3值差别较大,这时可以考虑采用加权的方法。即:

T1,T2,T3是求Z值时的权因子,可以根据3条轮廓外形线的形状,不断地调整该值,进而得到更加合适的分层厚度Z值。即若T1=0.1,T2=0.3,则T3=0.6;若T1=0.2,T2=0.3,则T3=0.5;若T1=0.3,T2=0.4,则T3=0.3;等等。总之,这3个权因子都取正值,而且其和必须等于1。它们的值可以根据式(1)不断选取新值。由于目前计算机的计算速度很快,所以不断调整权因子可以得到众多的Z值,再通过对比和分析,取得一个分层厚度Z的最优值。
2.2 基于STL模型的分层过程描述
对STL模型进行自适应分层的过程是,首先构建制件的CAD模型,然后在目前常用的CAD造型软件系统中将CAD模型转换为STL模型,对三维STL模型进行切片处理就是用一组平行的剖切面对该模型进行剖切,其实质就是剖切平面与STL模型求交的同时记录下截交线的数据,也就是求得分层切片的二维轮廓线,然后将该轮廓线的信息按照相应的数据结构进行存储。
在当前的UG,Pro/E,AutoCAD,CAXA等商用CAD软件系统中,都有求截面轮廓的功能和函数,调用已有的求截面命令或函数,可以得到精确的层片轮廓信息。因为AutoCAD是工程界家喻户晓、有口皆碑的优秀软件,利用AutoCAD的Section命令完成剖切,得出3条CAD模型的轮廓外形线,进而依据上述方法求出最优的分层厚度值。
在CAD系统中完成CAD模型并将其转换为STL模型后,再依据快速成型制件的形状,确定分层切片的方向。一般将该方向设置为Z轴方向,然后用所述的方法设定3条能基本反映模型形状的3条侧面轮廓外形线,再根据3条轮廓外形线的分段值进行加权来计算切片层厚,然后将计算得到的Z值存储。
基于STL模型的加权轮廓外形线的自适应分层的方法可描述如下:
Procedure
Begin{
Step1在AutoCAD环境里建立CAD模型;Step2转化CAD模型为STL模型;
Step3按照零件形状确定切片方向
(设置该方向为Z轴方向);
While do{
Step4初步确定切片厚度Z;
Step5调用AutoCAD命令(Section),用平行于
Z轴的3个平面分别剖切STL模型;Step6得到3条轮廓外形线L1,L2,L3;
Step7用2.1.2节的方法对轮廓外形线
进行分段判断等计算;
Step8再次调用AutoCAD命令(Section),用垂直于Z轴的平面分别分割3条轮廓外形线L1,L2,L3;
Step9根据3条轮廓外形线分别求得3个分层厚度值Z1,Z2,Z3;
Step10根据加权的方法计算切层的最终厚度

Step11求得切片厚度Z,再计算下一个对应的
切平面是H(i+1)=Hi+Z;
(其中H(i+1)和Hi是分层切片
时的Z坐标值)}
If{H(i+1)<Hmax时,Return(Step4);其中Hmax是三维实体在Z轴方向的最大值。}
Else
Step12完成三维实体的剖切,将有关数据按特定格式储存}End。
3 实例
在AutoCAD环境里,根据以上方法的过程进行了相关的实例制作和数据分析,对如图3所示的不规则零件分别用对STL模型均匀切片、面积变化率法和本文方法进行了计算分析。分析得出,对STL模型使用均匀切片方法时,切片厚度选取0.03 mm,切片后层数为336。用面积变化率进行自适应切片,最大切片厚度选择0.05 mm,最小切片厚度选择0.01 mm,切片后层数为256。用本文算法进行切片处理,允许的最大切片厚度为0.05 mm,最小的切片厚度为0.01,切片后层数为168。不仅如此,相比于STL模型均匀切片和用面积变化率进行自适应切片后的成型件,用本文算法切片处理后的成型件表面精度和质量更优。通过实例证明,该方法确实可行,计算简单,适应性强。无论对规则或不规则的零件都有很好的参考意义。

图3不规则零件的轮廓外形线
4 结束语
针对STL模型,提出的自适应分层方法,相比于传统的切片方法,不仅能够很好地提高切片的精度和效率,而且能很好地满足规则和不规则零件的精度要求。利用该方法对STL模型进行自适应切片,不仅比其它方法计算简单,而且比采用对STL模型进行均匀切片的方法的切片层数也要少得多。目前的大多数快速成型系统仍然采用STL模型,特别是对于形状不规则的制件,提出的方法相比之下确实另辟蹊径。可以充分利用计算机高速计算的优势,得出STL模型的多个不同的轮廓外形线的分层数据,然后进行对比再对比、分析再分析,进而达到制件的精度、质量、性能等方面的最佳效果。
[1] 刘伟军,等。快速成型技术及应用[M].北京:机械工业出版社,2005.
[2] ZHAO Z,LA PERRIERE L.Adaptive direct slicing of the solid model for rapid prototyping[J].International Journal of Production Research,2000,38(3):89- 98.
[3] 马永壮,刘伟军,董遇泰.基于有向加权图第归切片算法的研究[J].中国机械工程,2003,14(14):1221 -1224.
[4] 蔡道生,史玉升,黄树槐.快速成形技术中基于切片轮廓信息的自适应分层算法[J].机械科学与技术,2004,23(7):849- 851.
[5] Prashant Kulkarni,Debasish Dutta.An accurate slicing procedure for layered manufacturing[J],Computer- Aided Design,1996,28(9):683- 697.
[6] Mani K,Kulkarni P,et al.Region- based adaptive slicing[J].Computer Aided Design,1999,31(5):317 -333.
[7] Zhao Zhiwen,Luc Laperriere.Adaptive direct slicing of the solid model for rapid prototyping[J].International Journal of Production Research,2000,38(1):69 -83.
[8] 毕晓亮,朱昌明,侯丽雅.快速成型中的自适应切片方法研究[J].计算机应用研究,2002(4):21- 22.
[9] 林俊义,黄常标,江开勇.基于STL面片法向矢量的自适应分层算法[J],制造技术与机床,2003(11):68 -84.
[10] Pandey P M,Reddy N V,Dhande S G.A real time adaptive slicing for fused deposition modeling[J].International Journal of Machine tools and Manufacture,2003,43(1):61- 71.
Study on the Method of Adaptive Slicing Contour Line Based on STL Model
ZHOU Huiqun,WU Jianjun
(The Key Laboratory of Contemporary Design and Integrated Manufacturing Technology,Northwestern Polytechnical University,Xi’an 710049,China)
目前,大多数快速成型系统在表达CAD模型时仍采用STL模型。由于快速成型自身的特点,对STL模型进行分层处理是其必由之路。在分析了传统的STL模型分层方法的基础上,提出了一种基于STL模型的轮廓外形线自适应分层的方法,然后通过实例对该自适应分层方法进行了验证,证明了该方法的可行性和正确性。
快速成型;STL模型;轮廓外形线;自适应分层
At present,most rapid prototyping systems still use STL models when expressing CAD models.Due to the characteristics of rapid prototyping,layering on STL models is the only way.This paper analyzes the traditional slicing methods of STL models,and proposes a method of contour lines of adaptive slicing based on the STL model.The example of the adaptive slicing method has been verified,thereby proving the feasibility and accuracy of the method.
rapid prototyping;STL model;contour line;adaptive slicing
TP391
A
1001- 2257(2015)08- 0014- 04
周惠群 (1966-),男,陕西西安人,副教授,博士生,研究方向为CAD/CAM技术和快速成型技术。
2015- 04- 09
