桥式起重机箱型主梁的改进遗传算法优化设计

张 丹，俞齐鑫

（西安工程大学机电工程学院，陕西西安 710048）

桥式起重机箱型主梁的改进遗传算法优化设计

张 丹，俞齐鑫

（西安工程大学机电工程学院，陕西西安 710048）

0 引言

在实际的桥式起重机箱型主梁的优化设计中，通常会有多变量、多约束的问题出现［1］，一般目标函数与约束条件是非常复杂的，用传统的优化算法处理此类问题时达不到理想的状态，往往会出现收敛速度比较慢、容易陷入局部最优解，还有就是优化精度不高的问题。如今，运用新的优化方法来完善桥式起重机箱型主梁的设计，已经成为一种趋势。遗传算法（GA）［2］模拟了生物在自然环境进化中寻找全局最优解的过程，GA的原理比较简单、操作方便［3］，现已广泛应用于多个邻域。但是传统的遗传算法存在许多的不足，如收敛速度慢、早收敛和局部最优等［4］，会造成获得全局最优解的能力降低［5］。针对这些不足，提出了一种新的改进遗传算法。

1 遗传算法的改进

1.1 选择算子的改进

选择算子中一般采用较简单的轮盘赌选择法，该方法中个体被选择的概率与其适应度值的大小是成比例的，适应值越高的个体被选择的机会就越大，适应值较低的也有可能被选上。但是个体被选择的概率是随机和不准确的，也有可能导致最优个体一次都没有被选上，而劣质个体被选上好多次。为了不让群体中劣质个体被选上，让群体的发展更加优质，根据优胜劣汰的原则，提出了一种新的保留最优个体策略，保留了上一代种群中的最优个体，且使最优个体与其他个体进行交配时，能够找到更优个体。选择算子改进具体过程如图1所示。

图1 选择算子改进的原理

从图1看出，这里最优个体c1、c2、cn都是自己上一代种群中的最优个体，其中c1不参与交配，主要是为了保存上一代的最优个体并且完成更优变异，c2必须参与交配，采用轮盘赌方法依次对｛C3，C4，…，Cn－1｝群选择，假如选择到上一代的最差个体，则放弃重新选择，以达到择优的目的。新产生的｛c3，c4，…，cn｝个体群再根据交配概率Pc，作出是否参加交配的判断，分开c2与cn，是为了将上一代最优个体的优质基因更广地散播下去。

1.2 适应度函数的变化

遗传算法采用适应度函数值来评价个体性能，并指导整个搜索过程，其基本上不用搜索空间的知识，因此，适应度函数的选取相当重要。在遗传算法执行的不同期间，采用不变的或者比较差的适应度函数，很容易导致遗传算法出现欺骗问题［6］。遗传算法进化初期，可能会出现一些不凡的个体，这些不凡个体由于自身的竞争力优势反而控制着整个选择的过程，从而影响遗传算法全局优化的性能；遗传算法在接近收敛后期时，种群中每个个体的适应度相差甚小，如果再继续优化下去，很容易导致收敛到某个局部的最优解。

在机械设计中，当出现高维、非凸的目标函数且具有多约束条件时，常采用在目标函数转化为适应度函数时，将惩罚函数项加上不同的系数因子，这样在进化过程中可设置不同的阈值来改变因子的大小。具体的说，对于一般的优化问题，其数学模型为：

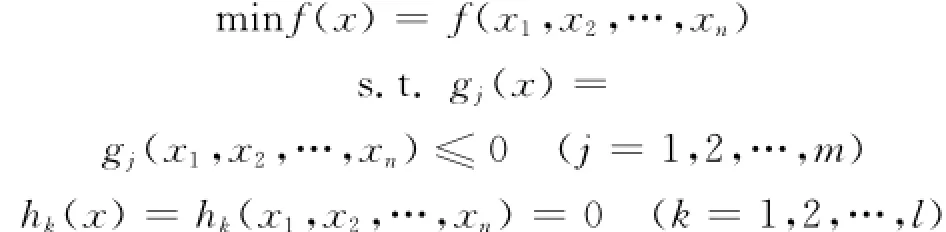
gj（x）为不等式约束；hk（x）为等式约束。

根据以上机械优化设计中的数学模型，一般把带有约束转化成无约束的优化问题，然后对其进行求解。也就是说，把约束函数和原目标函数通过内点惩罚函数法转化为新的适应度函数F（x，r），即

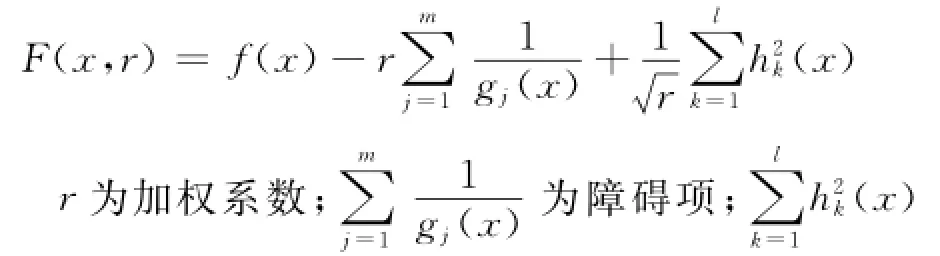
为惩罚项。

在实例中，首先设置不同的阈值，然后在算法进化早期和晚期改变r来调整适应度函数，最后避免在进化过程中导致出现欺骗问题。r的经验公式如下：

根据经验公式，可知r是依次递减的直到最后到0的数列，c为加权系数的缩减系数。c的大小在公式迭代过程中没有起到决定性的作用，在算法进化过程中，c取0.2～0.8之间的任何值。在算法进化早期，进化个体的平均适应度值远小于接近最优解时的平均适应度值，因此得需要加大惩罚项而减小障碍项，所以c一般取较小的值；若当进化个体的平均适应度值接近最优解的平均适应度值时，就应该加大障碍项而减小惩罚项，此时c取较大的值。

2 桥式起重机箱型主梁优化设计

以桥式起重机箱型截面主梁为例建立数学模型，采用常规fmincon、常规遗传算法和参考文献［5］以及本文改进遗传算法，对桥式起重机箱型主梁优化设计进行对比。

2.1 数学模型的建立

桥式起重机箱型主梁的计算简图及截面图如图2所示。在保证主梁性能的条件下，使箱型主梁重量最轻，然而箱型主梁的重量主要取决于箱型主梁的截面面积，所以以箱型主梁的截面面积最小为优化目标。则数学模型如下：

图2 起重机箱型主梁的计算简图及截面图

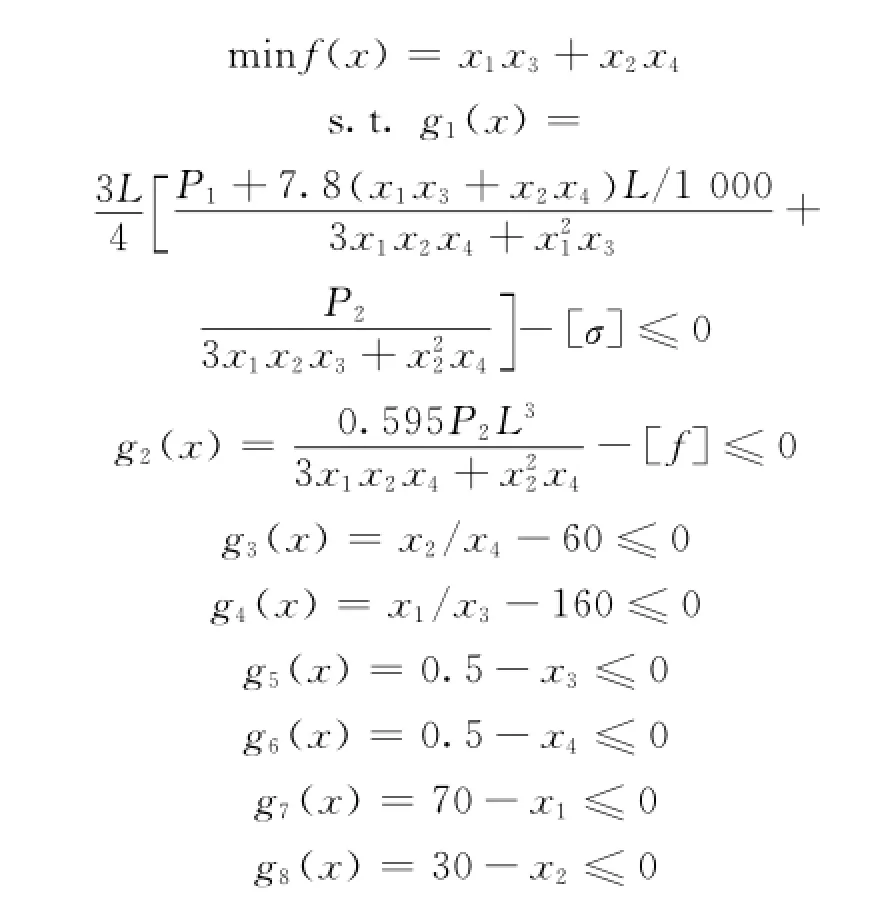
x1为主梁腹板高度；x2为主梁翼缘板宽；x3为腹板厚度；x4为翼缘板厚度。参数：L＝10.5 m；［f］＝L／700；P1＝117 679.8 kPa；P2＝1 176 798 k Pa；［σ］＝137 293.1 k Pa。

2.2 实例验证

桥式起重机箱型主梁的优化，首先采用本文方法，将以上约束条件和原目标函数通过惩罚函数法转化为新的目标函数：

参数设置：Pc＝0.9，Pm＝0.09。然后在Matlab软件中，分别采用工具箱中fmincon函数、Matlab遗传优化工具箱gatool和参考文献［5］的方法进行编程实现，其结果如表1所示。

表1 4种优化方法获得箱型主梁截面积优化结果对比表

从表1中看出，采用本文方法获得的最优解明显优于其他算法获得的最优解，且从迭代运行所占用的时间统计上看，本文方法平均用了44 s，其值明显小于传统遗传算法优化方法，即在整个优化过程中，本文方法优化所用的时间要比其他优化方法少得多，也就是说本文方法的计算效率高。

3 结束语

提出一种新的改进遗传算法，解决了常规遗传算法对桥式起重机箱型主梁优化设计中，存在收敛早熟和收敛速度慢的问题。首先该算法对选择算子进行改进，选择算子采用保留最优策略实现了群体优胜劣汰，然后再通过时刻改变惩罚项和障碍项动态调整适应度函数。通过对桥式起重机箱型主梁优化设计实例的验证，证明了本改进算法的求解精度较高，收敛速率快，且能很好地避免落入到局部最优，提高了桥式起重机箱型主梁的优化设计性能。

［1］ 董威.基于Pareto遗传算法的起重机主梁优化设计［D］.大连：大连理工大学，2005.

［2］ 孟鑫.基于改进免疫遗传算法的桥式起重机主梁优化设计［D］.太原：中北大学，2014.

［3］ 梁兴建，詹志辉，谭伟，等.基于最优保留策略的改进遗传算法［J］.计算机工程与设计，2014，35（11）：3985-3990.

［4］ Ritthipakdee A，Thammano A，Premasathian N，et al.A new selection operator to improve the performance of genetic algorithm for optimization problems［C］／／IEEE ICMA Conference International Scientific Advisory Board，2013：371-375.

［5］ 刘道华，原思聪，张锦华，等.粒子群参数自适应调整的优化设计［J］.农业机械学报，2008，39（9）：134-137.

［6］ Gen M，Yun Y.Soft computing approach for reliability optimization：state-of-the-art survey［J］.Reliability Engineering and System Safety，2006，91（9）：1008-1026.

Optimized Design for Box Girder of Bridge Crane Based on Improved Genetic Algorithms

ZHANG Dan，YU Qixin
（College of Mechanical and Electrical Engineering，Xi’an Polytechnic University，Xi’an 710048，China）

在遗传算法原理的基础上，首先对遗传算法中的选择算子进行改进优化，将优胜劣汰的思想融入到遗传算法中，从而保障最优基因能迅速地遗传到后代，加速收敛。然后通过时刻改变惩罚项和障碍项动态调整适应度函数，避免算法止于局部最优。最后，将改进的遗传算法应用于桥式起重机箱形主梁的优化设计中。

遗传算法；桥式起重机；箱型主梁；优化设计

Based on the principle of genetic algorithms，this paper first improves and optimizes the selection operator of genetic algorithm，bringing the principles of“survival of the fittest”into the frame of the genetic algorithms，thus faster transmission of the elitist genes into the later generations and the increase of the convergence speed is guaranteed；and then the dynamic change of fitness function is realized through the dynamic changes of barrier items and penalty items，so as to achieve the global convergence of the algorithm.Finally，the improved genetic algorithm is applied to the optimized design of the box girder of bridge crane.

genetic algorithm；bridge crane；box-type girder；optimized design

TH215；TP202

A

1001-2257（2015）09-0021-03

张 丹（1990－），女，陕西渭南人，硕士研究生，主要研究方向为机电控制。

2015-04-20