正交试验法在气体分析仪自动校准装置数据验证中的应用*
2015-06-09王东丽
李 博 王东丽
(河南省计量科学研究院,郑州 450008)
正交试验法在气体分析仪自动校准装置数据验证中的应用*
李 博 王东丽
(河南省计量科学研究院,郑州 450008)
以En值的绝对值为试验目标,采用正交试验法对气体分析仪自动校准装置进行了数据验证,验证结果表明,该装置输出的目标浓度值的气体和使用相同浓度的二级气体标准物质在各自的不确定度范围内等效一致,对数据进行了极差分析和方差分析,结果表明气体总流速及目标气体的组分数对输出量值的影响较大。
正交试验;校准装置;数据验证;极差分析;方差分析
0 引言
气体分析仪自动校准装置是专为气体分析仪的检定和校准设计开发的一种新型装置,该装置以流量比混合法为基本原理,通过严格控制一定比例的标准气体和稀释气体的流量,并加以混合而制得目标浓度的气体[1]。该装置集浓度计算、配制气体、控制流量和数据处理于一体,自动化程度高,操作简便,可连续配制并供给浓度值连续可调的多组分混合标准气体。为确认该装置量值的准确性和稳定性,并分析各个影响因素对装置输出量值的影响,必须对不同工作条件下装置的输出量值进行试验验证。
正交试验法于上世纪60年代初传入我国,是利用正交表来安排与分析多因素试验的一种设计方法。它是由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验,通过对这部分试验结果的分析了解全面试验的情况,找出最优的水平组合。其基本特点是:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全面试验的情况[2-4]。正交试验法在我国已被广泛应用于材料、化工、农业和环境等研究领域,作为一种通用的试验方法,其用于计量标准设备数据验证的实例还未见报导。本文将正交试验法应用于气体分析仪自动校准装置的数据验证,且与正交试验法在其他领域的应用不同,本试验的试验指标并非一个由试验直接得到的测量结果,而是采用En值的绝对值作为试验指标。
1 实验部分
1.1 实验仪器与工作条件
1)气体分析仪自动校准装置样机一台;
2)纯度为99.999%的高纯氮气5瓶;
3)浓度为3.01%mol/mol的CH4标准气体一瓶,相对不确定度为0.5%;
4)浓度为34.92%mol/mol的CH4标准气体一瓶,相对不确定度为0.5%;
5)浓度与目标气体量值一致的二级标准气体,共计25瓶,相对不确定度为1.0%;
6)量程分别为0~10MPa的减压阀6个;
7)量程为0~5%mol/mol的经校准的CH4红外分析仪一台。
1.2 实验方法
1.2.1 试验目标
气体分析仪自动校准装置共有ABCDEF六个气路,其中A气路固定使用稀释气体,BCDEF气路使用标准气体,将经装置稀释配制而成的目标气体通入红外分析仪,其示值作为测量值,记为X,将与目标气体量值一致的二级标准气体直接通入红外分析仪,其示值作为参考量值,记为Y。通过En值的方法判断两种方法在各自不确定度范围内是否等效,并将En值的绝对值作为正交试验的试验指标[5-6]。En值公式计算如下:
C=X-Y
(1)
式中:C为测量值与参考量值的差值;UX为装置配制的目标气体在红外分析仪上的示值X的扩展不确定度,主要包含被稀释标准气体、校准装置、红外分析仪示值稳定性、重复性、分辨力和线性等的不确定度贡献;UY为与目标气体量值一致的二级标准气体在红外分析仪上的示值Y的扩展不确定度,主要包含与目标气体量值一致的二级标准气体、红外分析仪示值稳定性、重复性、分辨力和线性等的不确定度贡献。
1.2.2 影响因素
由于各气路所用流量计的个体差异,使用不同气路配制的相同浓度目标气体之间存在差异,由于A气路固定使用稀释气体,本试验主要考察目标组分分别位于其他几个气路时对试验目标的影响情况;对于同一气路而言,由于流量计在整个工作区间的不同位置精度不尽相同,例如某路流量计的量程为500mL/min,其10%量程输出和50%量程输出的精度也不相同;当配制气体为多组分时,目标组分的气体浓度由该组分所在气路与其他气路的流量比共同确定,组分数不同,目标组分的测量值也会受到影响;输出气体的总流量可以设置,总流量不同,也会对目标组分的测量值产生影响。以上为对试验目标有影响的4个主要因素,根据实际工作经验,对以上每个因素确定5个水平,试验因素及水平表见表1。
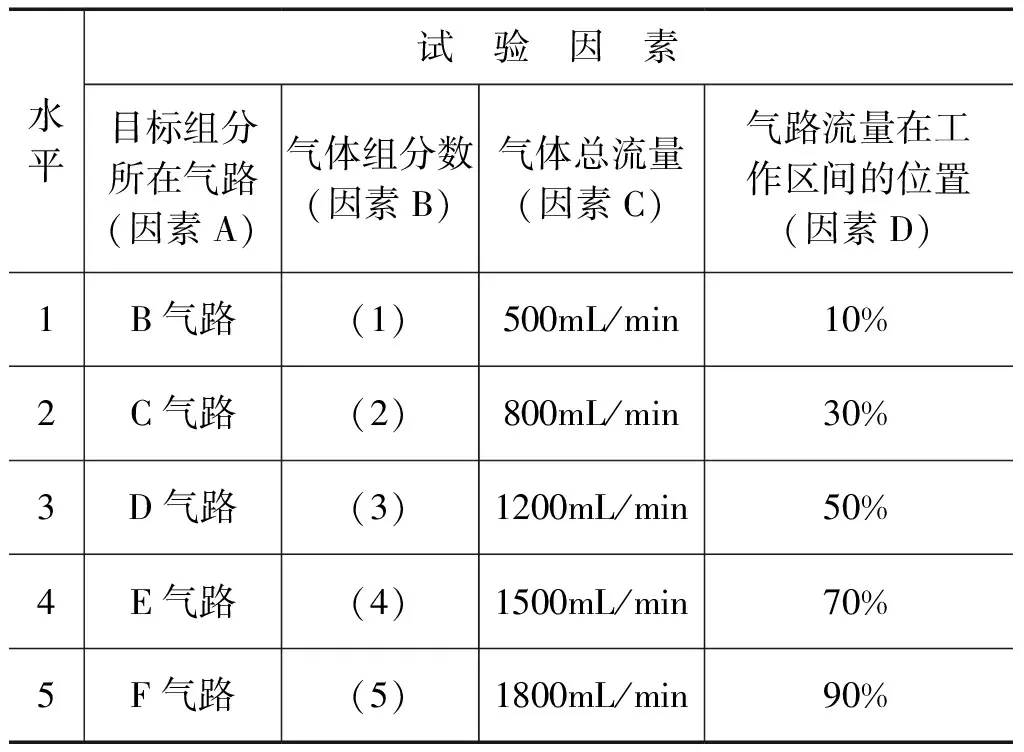
表1 试验因素水平表
1.2.3 实验设计
根据上面提供的因素和水平,如果进行全面试验,需要做54即625次试验,显然不太实际。所以,本文应用正交试验法设计实验序列,以期通过较少的试验次数达到全面的试验效果。设计正交试验需要进行正交表的选择,选择的方法为试验的水平作为正交表的水平,试验的各个因素小于或等于正交表的列数。本试验选用L25(56)作为该试验考察试验指标的正交表。因为上面各因素之间相互独立,没有交互作用,我们把上述各因素放在正交表的列位置,把每一个因素的水平放在正交表的行位置,这样就构成了完整的表头设计。设计好的试验序列见表2。
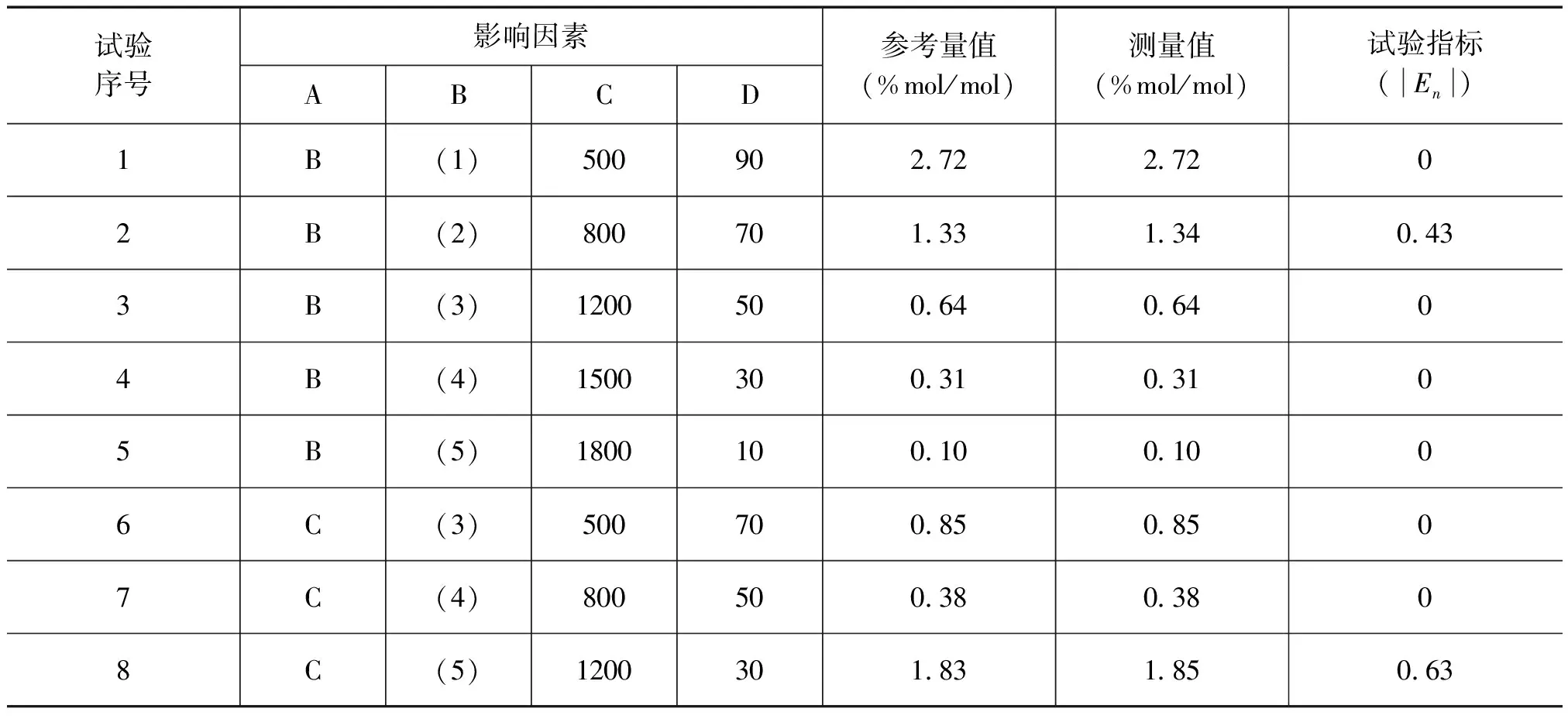
表2 试验序列及试验指标结果
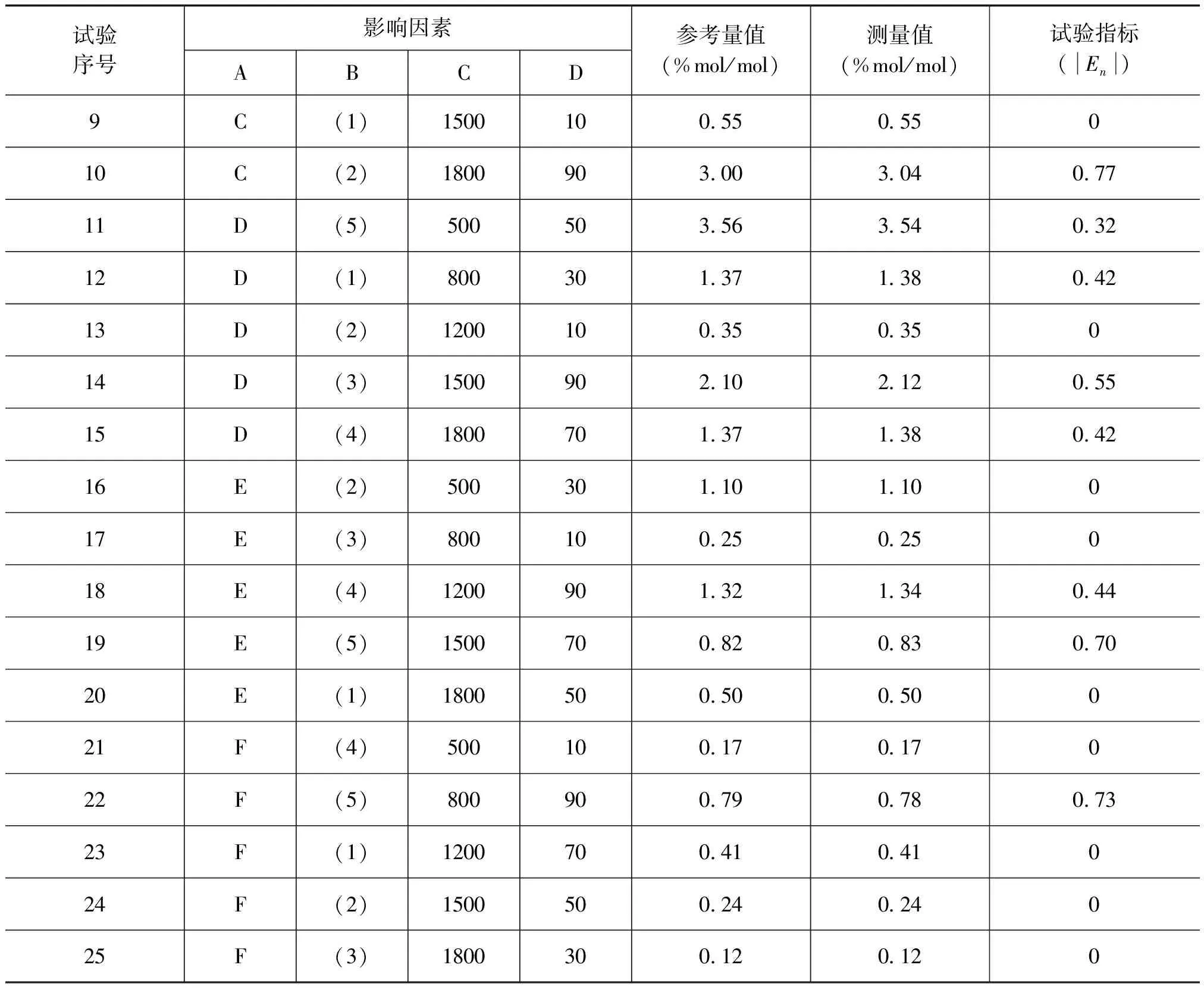
续表
由试验序列可见,任一列中,各水平都出现,且出现的次数相等,使得部分试验中包括了各个因素的所有水平;任两列之间各种不同水平的所有可能组合都出现,且出现的次数相等,即每个因素的任一个水平与另一因素的各个水平的所有可能组合次数相等,这使得任意两列各个水平之间的搭配是均匀的;任两列的所有水平组合都出现,使任意两因素间的试验组合为全面试验。
2 数据分析
2.1 试验指标直观分析
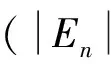
2.2 极差分析
为了进一步分析各个影响因素对试验目标的影响程度,对实验数据进行了极差分析,分析过程及结果见表3。其中,Ki为各个因素i水平所对应的试验指标和,ki为Ki的平均值;Rj为第j列因素的极差,反映了第j列因素水平波动时,试验指标的变动幅度。以因素A为例,由表1可知,当目标气体所在气路为B气路时,因素A的水平为1,查表2的数据进行计算,因素A第1水平所对应的试验指标之和为:K1(A)=0.43,则平均值k1(A)=0.09,同理可分别得到k2(A)、k3(A)、k4(A)、k5(A),最终得到第一列即A因素的极差为:R1=0.25。Rj越大,说明该因素对试验指标的影响越大。由表3可见,R4及R2较大,说明根据极差分析的结果,因素D及因素B对试验指标的影响较大,因素A及因素C对试验指标的影响相当。
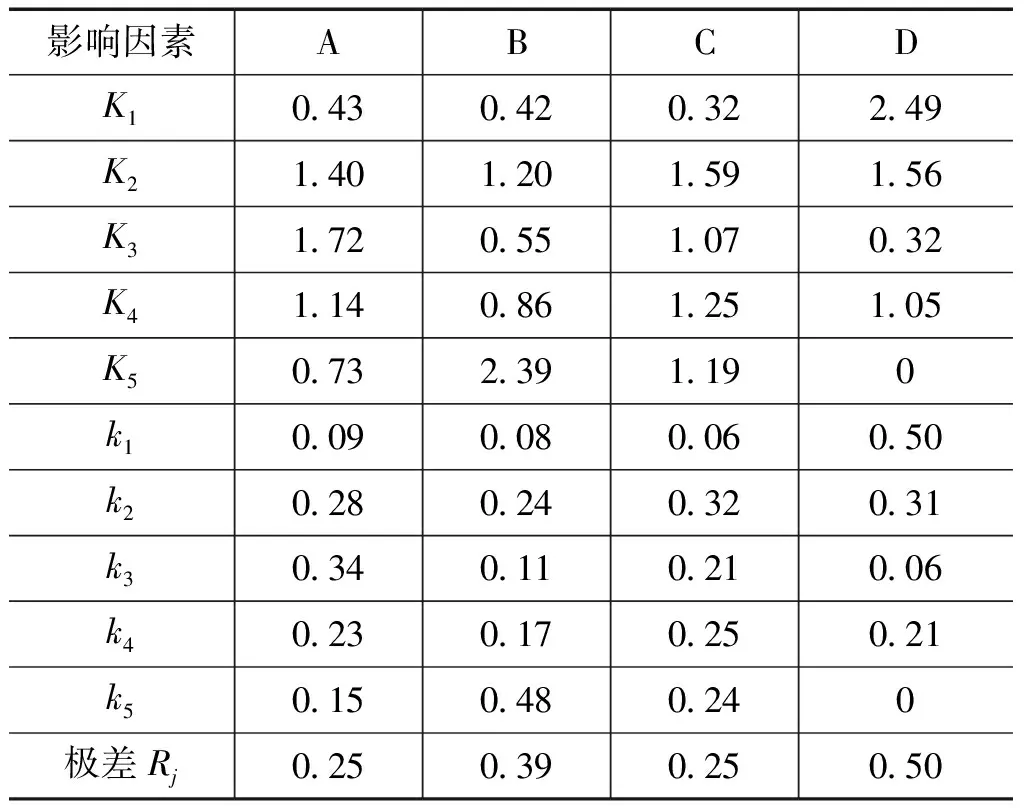
表3 极差分析结果
2.3 方差分析
极差分析法简单易懂,只需对试验结果作少量处理,即可得到最佳配合比及各因素影响程度,但极差分析无法区分某因素各水平所对应的差异究竟是因素水平不同引起的,还是试验误差所引起的。为此,我们对数据进一步进行方差分析及显著性检验。方差分析是把实验数据总的波动(即数据的总的偏差平方和s总)分解成两部分:一部分反映因素水平变化引起的波动(即因素的偏差平方和),另一部分反映试验误差引起的波动(即误差的偏差平方和se)。
进行方差分析需要计算各个因素及误差的偏差平方和,为了消除个数不同对实验指标所产生的影响,应采用平均偏差平方和,以因素A为例其计算公式为:sA/fA,误差的平均偏差平方和为:se/fe。其中sA、se分别代表因素A和误差的偏差平方和,fA和fe分别代表sA和se的自由度。因素水平的变化引起的平均偏差平方和与误差的平均偏差平方和的比值称为F值,方差分析结果见表4。
由表4可见,四个因素的F值均大于1,说明因素水平的变化对试验指标的影响均超过了试验误差所产生的影响。为了判断因素对试验指标影响的是否显著,须将计算得到的F值与从F分布表上查到的相应临界值进行比较。当F值大于临界值时,表明该因素对实验结果影响显著。分别取显著因子a=0.10及a=0.05,查F分布表得:F0.10(4,8)=2.81,F0.05(4,8)=3.84。由表4结果可知:由于FB>F0.10(4,8),所以,有90%以上的把握判断因素B的水平改变对实验结果有显著影响,同理,由于FD>F0.05(4,8),有95%以上的把握判断因素D的水平改变对实验结果有显著影响,这也与极差分析的结论相一致。
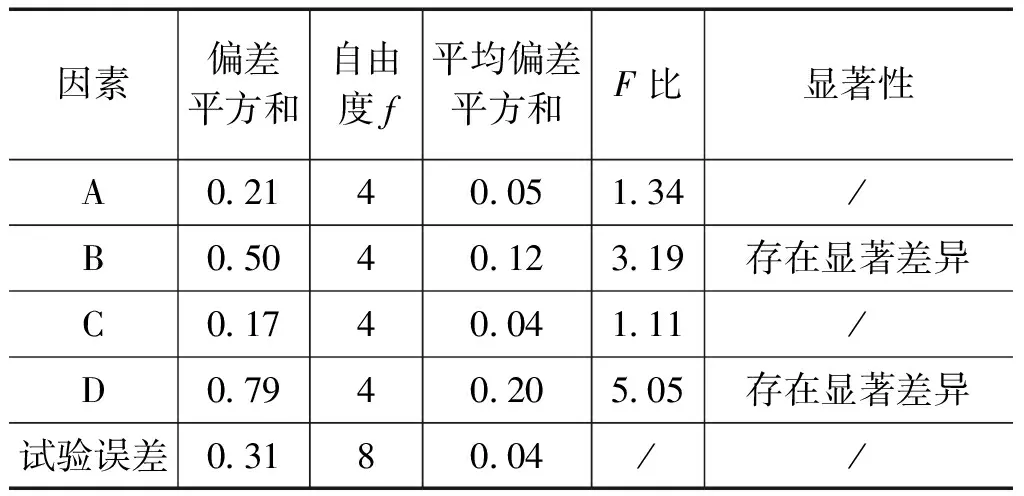
表4 方差分析结果
3 结论
应用正交试验法对气体分析仪自动校准装置进行了数据验证,结果表明,气体分析仪自动校准装置在不同工作条件和设定参数下,其输出的目标气体浓度值和使用相同浓度的二级气体标准物质在各自的不确定度范围内等效一致;对结果进行了极差和方差分析,结果一致表明,气体总流速及目标气体的组分数对输出值的影响较大。
[1] 王东丽.便携式智能气体配装置的设计[J].计量技术,2013(6)
[2] 方开泰,马长兴.正交与均匀试验设计[M].北京:科学出版社,2001
[3] 邓勃.分析测试数据的统计处理方法[M].北京:清华大学出版社,1995
[4] 郝拉娣,于化东.正交试验表的使用分析[J].编辑学报,2005,17(5)
[5] 中国计量测试学会.一级注册计量师基础知识及专业实务[M].北京:中国计量出版社,2012
[6] 倪育才.实用测量不确定度评定[M].北京:中国计量出版社,2012
国家质检总局科技计划项目“气体分析仪自动校准装置”(T2009-HAQTS-0031)
10.3969/j.issn.1000-0771.2015.4.06
