掠入射X射线反射法测量纳米尺度氮化硅薄膜厚度*

高慧芳 任玲玲 贾亚斌

(1.中国计量科学研究院，北京 100029；2.太原理工大学，太原 030024)



掠入射X射线反射法测量纳米尺度氮化硅薄膜厚度*

高慧芳1任玲玲1贾亚斌2

(1.中国计量科学研究院，北京 100029；2.太原理工大学，太原 030024)

掠入射X射线反射法是一种薄膜厚度的无损测量方法。采用掠入射X射线反射法测量纳米尺度氮化硅薄膜厚度，拟合模型的建立和测量条件的选择是测量结果准确性的重要影响因素。研究建立了合理的拟合模型，并研究了不同功率、不同步进及每步不同停留时间对测量结果的影响。结果表明，电压40kV、电流40mA、步进0.004°、每步停留时间2s为最佳的测量条件。

掠入射X射线反射法；氮化硅；薄膜厚度

0 引言

纳米尺度氮化硅薄膜具有硬度高、熔点高、热稳定性好、机械强度高、耐腐蚀以及优良的光电性能、阻挡杂质粒子扩散和抗水汽渗透能力等特点，广泛应用在半导体、光电子、微电子、太阳能电池、航空航天、量子器件等领域，例如内层介电绝缘膜、场效应管(或薄膜晶体管)的栅极绝缘层、抗蚀层、钝化保护膜等[1]。薄膜的物理性能与薄膜的厚度密切相关，所以薄膜厚度的准确测量对于其物理性能的控制非常重要[2-3]。薄膜厚度的表征方法有X射线光电子能谱(XPS)、俄歇电子能谱(AES)、透射电镜(TEM)、椭偏(SE)和掠入射X射线反射法(GIXRR)等。其中，掠入射X射线反射法较其它方法具有很多优点，它是一种测量薄膜厚度的无损、绝对方法，对样品没有限制，可以准确测量单层及多层薄膜的厚度、密度、粗糙度等有价值的结构信息，厚度范围从几纳米到几百纳米[4-6]。但是，掠入射X射线反射法测量只能得到一条没有量值的曲线，需要后续通过Parratt递推公式进行拟合[7]。因此测量方法的建立不仅与测量条件有关，而且与拟合过程有关。测量条件包括功率(电压/电流)、步进、每步时间等；而拟合模型的建立是拟合过程的关键[8]。日本、韩国等国家计量院都开展了纳米薄膜的结构、组成及特性量的测量技术研究。中国计量科学研究院之前对掠入射X射线反射法测量分子束外延生长的GaAs/AlAs超晶格的厚度测量进行了研究，其测量的准确性也得到了验证[9]。

在本文中，通过掠入射X射线反射法测量纳米尺度氮化硅薄膜，在不同功率(35kV×40mA、40kV×40mA、45kV×40mA)，不同步进(0.002°、0.004°、0.006°)，及不同停留时间(1s、2s、3s)下研究了拟合模型、测量条件对测量结果的影响。

1 实验方法

通过电感耦合等离子体化学气相沉积法，在硅基底上制备了厚度名义值为50nm的Si3N4薄膜。使用PANlytical公司的X’pert MRD型X射线衍射仪在光路校正后对薄膜样品进行掠入射X射线反射测量。通过采用不同单色器单色化入射X射线，将入射光源溯源至单晶硅晶格参数；采用溯源至SI国际单位的激光干涉仪和自准直仪分别对X射线衍射仪的θ角、2θ角进行校准[10-11]。仪器的射线源为Cu Ka (波长l =0.15419nm)，试验过程中采用ω-2θ模式扫描，使用X’Pert reflectivity软件进行测量曲线拟合。

2 结果与讨论

2.1 拟合模型

为了得到拟合结果，首先假定拟合模型为简单的两层模型(模型Ⅰ，见表1)，即Si基底上生长一层Si3N4薄膜。通过实验数据与模型的拟合结果分析，如图1所示，拟合图形与测量的反射曲线相差较大，无法体现反射曲线的振荡特性，即使改变各层的密度、厚度和粗糙度也不能满足拟合的需要，故需要进一步分析样品，重新建立拟合模型。

表1 拟合模型Ⅰ

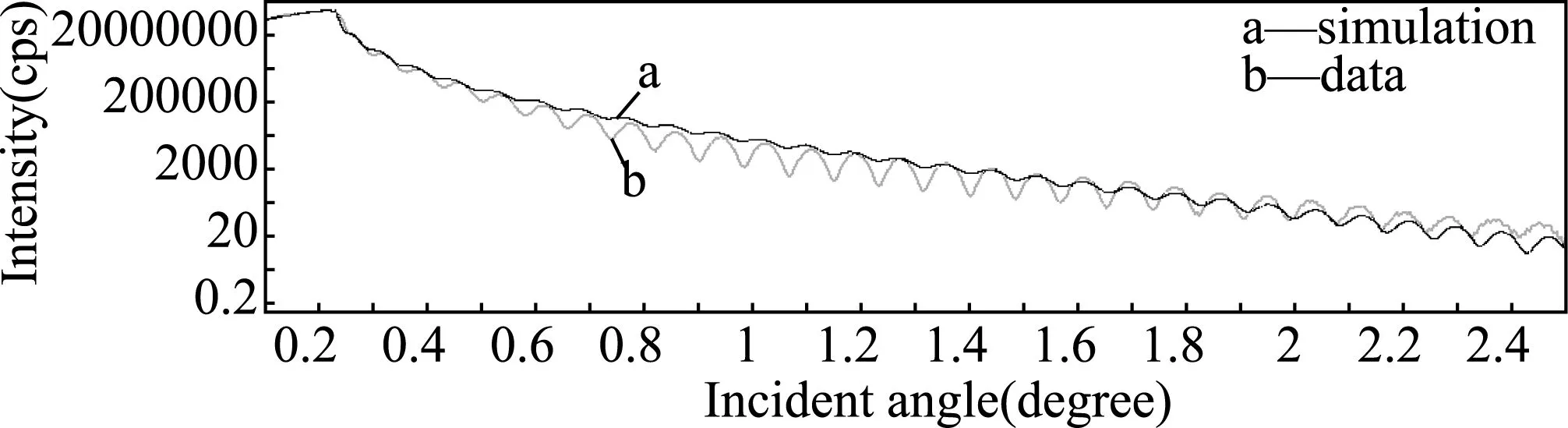
图1 以模型Ⅰ拟合的Si3N4薄膜反射曲线的拟合图形

考虑到Si3N4薄膜与Si基底之间不是理想界面，基底在薄膜沉积前及沉积过程中可能会自然氧化，吸附潮气和杂质，同时界面附近材料会相互渗透，所以假设拟合模型在薄膜和基底之间增加一层界面层。之后，薄膜样品在储藏、使用中，薄膜表面与空气界面吸附杂质、水分、碳氢化合物等，所以拟合模型在Si3N4薄膜层上增加一层表面污染层。拟合模型如表2中模型Ⅱ所示，拟合结果见图2，拟合曲线与测量曲线得到了很好的匹配，说明建立的拟合模型合适，拟合数据可靠。故选择模型Ⅱ作为氮化硅薄膜测量曲线的拟合模型。

表2 拟合模型Ⅱ

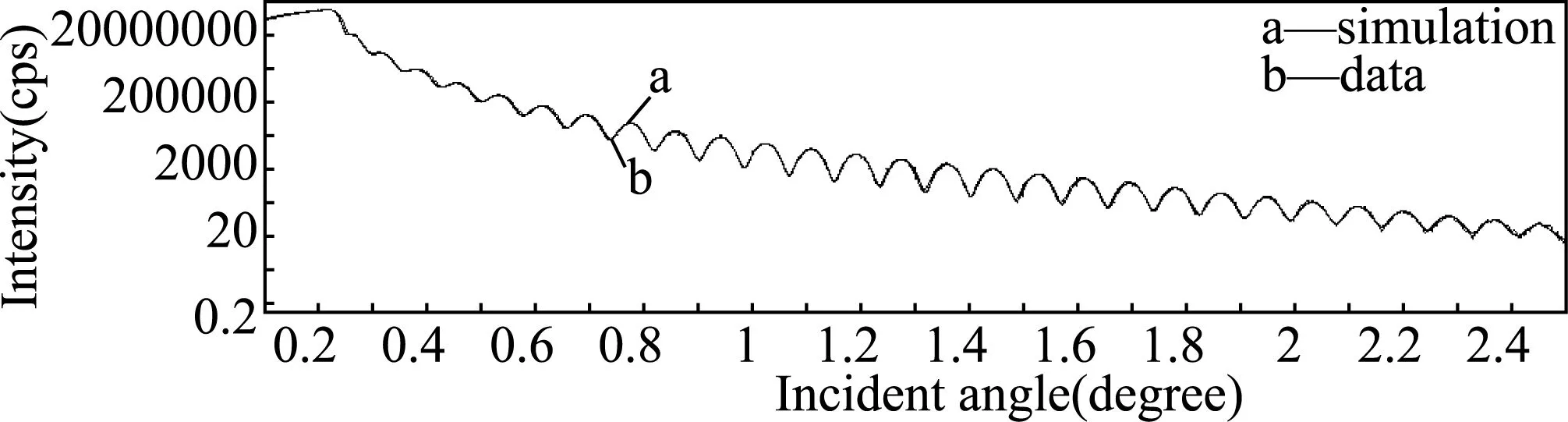
图2 以模型Ⅱ拟合的Si3N4薄膜反射曲线的拟合图形

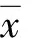
(1)

式中，xi为第i次拟合的结果；n为拟合次数。

标准偏差sr为

(2)

(3)

式中，r为重复性；xm和xn为彼此独立的拟合结果。

r=2.83sr

(4)

拟合结果满足公式(3)、(4)的要求，则认为结果是可靠有效的。基于以上公式，每条测量曲线至少进行3次有效拟合，每次有效拟合都作为一次拟合结果。

2.2 测量条件

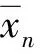
(5)

式中，m为重复测量次数；nm为测量曲线的有效拟合次数。

合并样本标准偏差sp为

(6)

式中，sm为测量曲线多次拟合的标准偏差。

合并样本标准偏差可以作为测量条件选择的依据。

固定电流为40mA，步进为0.004°，每步停留时间为2s，在不同电压(35，40，45kV)条件下对薄膜厚度进行重复测量。计算得到不同电压测量条件下的薄膜厚度合并样本平均值、合并样本标准偏差，见表3。

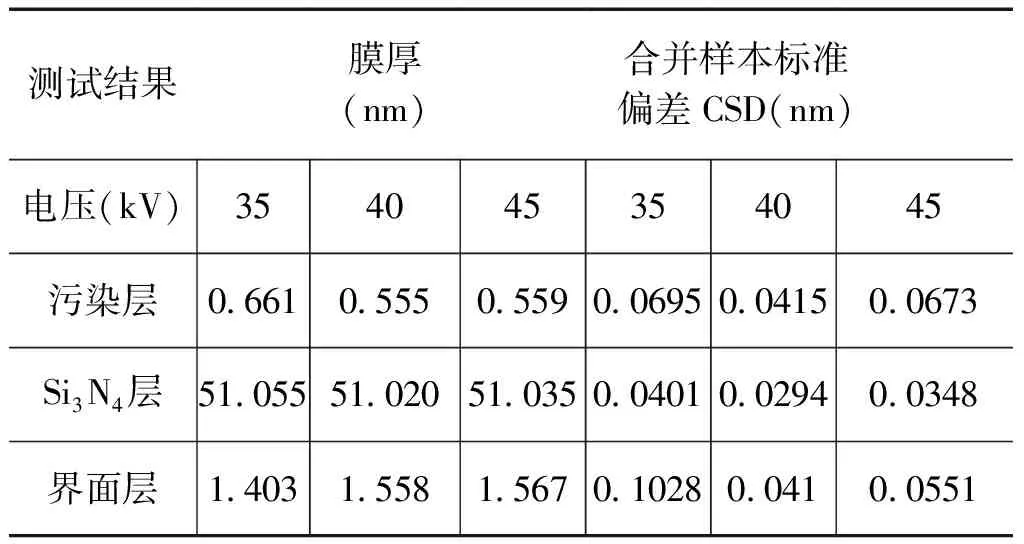
表3 不同电压测量条件的拟合结果

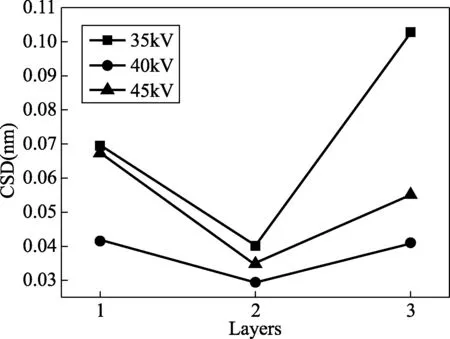
图3 不同电压测量条件下的拟合结果合并样本标准偏差

从表3中可以看出，电流一定，不同电压下测量得到的每层膜厚平均值相差不大，较高电压40、45kV下测量得到的每层膜厚平均值更为接近。在不同电压下各层膜厚合并样本标准偏差如图3所示。电压为35kV时膜厚合并样本标准偏差最大；电压为40kV时膜厚合并样本标准偏差最小。分析原因可能是，当电压较低为35kV时，产生的X射线能量较低，测量得到的信号噪音相对较大，造成拟合结果准确性降低，不确定度增大。当电压较高为45kV时，虽然反射信号增强，信噪比高，反映的结构更为精细，但达到仪器的操作上限，设备的稳定性降低，使得不确定度增大。电压为40kV时，反射强度和信噪比适中，因此测量过程中在电流40mA一定时，选择40kV的电压进行测量。

固定电流为40mA，电压为40kV，每步停留时间为2.00s，步进分别为0.002°、0.004°和0.006°条件下对薄膜厚度进行重复测量。计算得到不同步进测量条件下的薄膜厚度合并样本平均值、合并样本标准偏差，见表4。

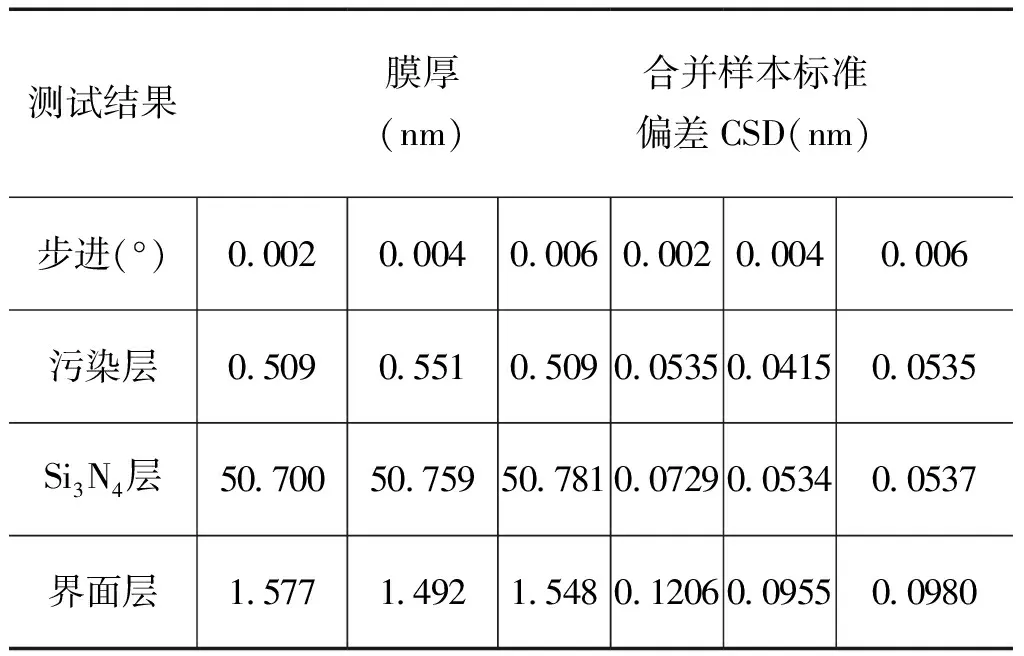
表4 不同步进测量条件的拟合结果

从表4可以看出，不同步进测量条件下的膜厚平均值相差不大。但是步进较小为0.004°时，厚度合并样本标准偏差最小，见图4。分析原因，采样步进较小时，采集的数据个数增加，分辨率较高，反映的结构更为精细，但是每步的强度总计数较小，信噪比减小，计数误差大，所以拟合结果的准确性会有所降低。采样步进较大，数据的采集个数减少，数据处理量减少，每步强度总计数大，计数误差较小，但是步进太大会降低分辨率。因此，测量过程采用步进0.004°测量较好。

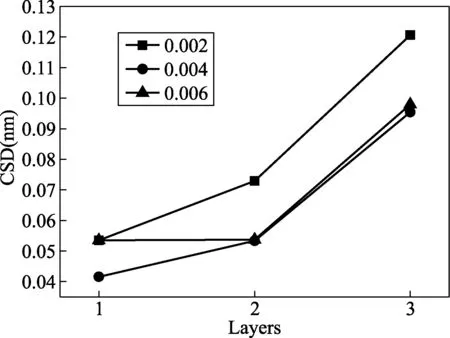
图4 不同步进测量条件下的拟合结果合并样本标准偏差

相似，固定电流为40mA，电压为40kV，步进为0.004°，每步停留时间分别为1s、2s和3s条件下对薄膜厚度进行重复测量。计算得到每步不同停留时间测量条件下的薄膜厚度合并样本平均值、合并样本标准偏差，见表5。

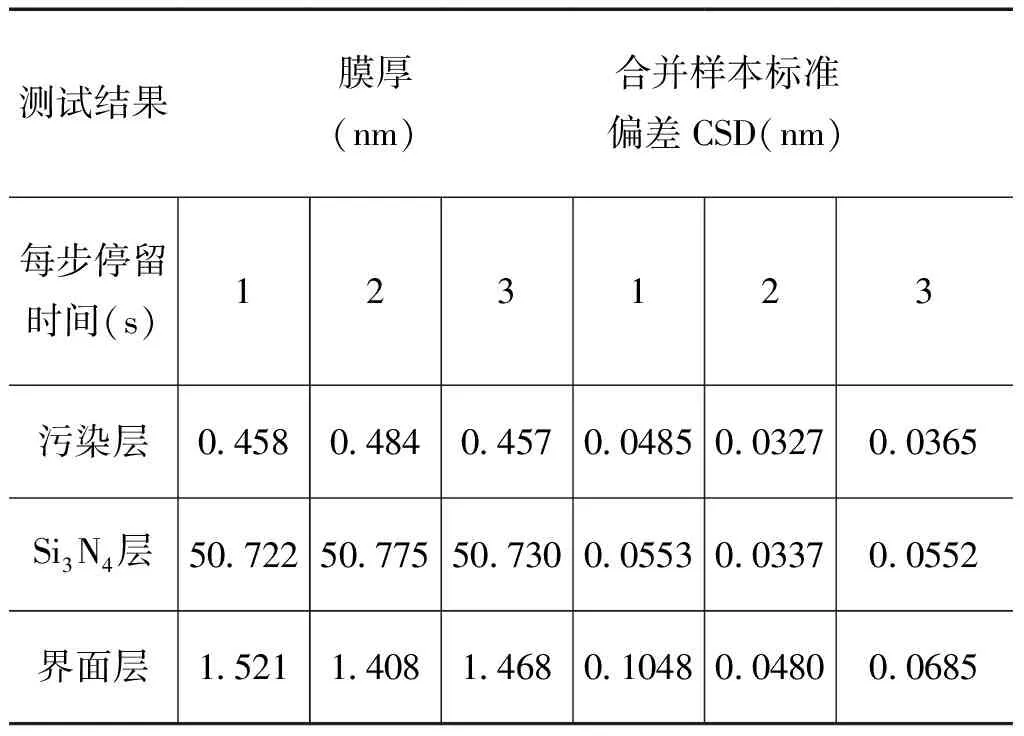
表5 每步不同停留时间测量条件的拟合结果

从表5可以看出，每步停留时间为2s时，每层膜厚平均值与每步停留时间为1s和3s的膜厚平均值相近。但是从图5可以看出每步停留时间为2s的各层厚度合并样本标准偏差较小。分析原因可能是，每步停留时间较短时，采集的信号量少，噪音相对较大，对样品反映不全面，不确定度较大；每步停留时间若延长，可减小计数统计误差，提高准确度与灵敏度，但时间过长将损失工作效率，而且采集的噪音增大。因此测量条件选择每步停留时间2s较好。

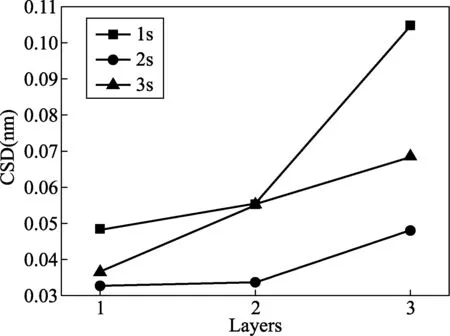
图5 每步不同停留时间测量条件下的拟合结果合并样本标准偏差

3 结论

采用掠入射X射线反射法测量厚度名义值为50nm的氮化硅薄膜。为了得到准确的薄膜厚度，从测量条件的选择和拟合模型的建立两个方面进行了研究。通过样品分析建立了合理的拟合模型，即污染层/氮化硅层/界面层/硅基底，测量曲线与拟合曲线很好匹配。研究了测量条件对测量结果的影响，采用合并样本标准偏差作为选择测量条件的依据。结果表明，测量条件为电压40kV、电流40mA、步进0.004°、每步停留时间2s时，膜层厚度的合并样本标准偏差较小，为最佳的测量条件。

[1] 张化福，祁康成，吴健.氮化硅薄膜的制备方法及主要应用[J].材料导报,2004,18(z2):298-300

[2] Futako W,Mizuochi N, Yamasaki S. In situ ESR observation of interface dangling bond formation processes during ultrathin SiO2growth on Si(111) [J]. Phys Rev Lett, 2004, 92: 105505

[3] Gayathri N, Banerjee S. Layering of ultrathin SiO2film and study of its growth kinetics [J]. Appl Phys Lett, 2004, 84(25): 5192-5194

[4] Colombi P, Bontempi E, etal. X-ray reflectivity and total reflection x-ray fluorescence study of surface oxide evolution in a GaAs/AlAs multilayer system [J]. J Appl Phys, 2009, 105: 014307

[5] Stoev K, Sakurai K. Recent theoretical models in grazing incidence X-ray reflectometry [J]. The Rigaku Journal, 1997, 14: 22-37

[6] Kojima I, Li B. Structural characterization of thin films by X-ray reflectivity [J]. The Rigaku Journal, 1999, 16(2): 31-41

[7] Parratt L G. Surface Studies of solids by total reflection of X-Rays [J]. Phys Rev, 1954, 95: 395-369

[8] Kim C, Koo T, Choi Y. Observation of an interlayer in a nano-scale SiO2layer on Si substrate by X-Ray reflectivity (XRR) analysis [J]. Solid State Phenomena, 2007, 124-126: 1689-1692.

[9] Ren L L, Gao H F, Yuan A L. Effects of growth conditions on the GaAs/AlAs superlattices by grazing incidence X-Ray reflectivity [J]. J Nanosci Nanotechnol, 2013, 13(2): 761-765

[10] 任玲玲，崔建军. X射线衍射仪的角度溯源[J]. 计量技术, 2012(3): 48-51

[11] 任玲玲，高慧芳. X射线衍射仪的X射线溯源[J]. 计量技术, 2012(8): 3-5

*课题项目：中国计量科学研究院基本科研业务费AKY1330

10.3969/j.issn.1000-0771.2015.4.02