应变式扭矩传感器应变系数的测量结果不确定度评定
2015-06-09谭琦瑛曹金宏
谭琦瑛 曹金宏 罗 刚 王 喻
(湖北机电院机械产品质量检测中心,武汉 430070)
应变式扭矩传感器应变系数的测量结果不确定度评定
谭琦瑛 曹金宏 罗 刚 王 喻
(湖北机电院机械产品质量检测中心,武汉 430070)
结合工作实际,阐述了用DBSL-3t拉压力传感器作为测量标准,测量8000N·m应变式扭矩传感器应变系数的方法,并就其测量结果不确定度进行探讨。
扭矩传感器;应变系数;测量不确定度;评定
0 引言
通过多点重复测量8000N·m应变式扭矩传感器系数,评定其测量结果的不确定度,规范实验室开展的内部校准活动,保证量值溯源有效,确保示值准确性。
1 概述
1.1 环境条件
温度(20±5)℃;相对湿度≤80%RH。无影响正常工作的振动冲击,无强电磁干扰,测量对象和测量标准均确保正常。
1.2 主要仪器设备
DBSL-3t拉压力传感器配仪表(测量标准,以下简称拉压力传感器),示值误差±0.30%;LC1007静态应变仪(以下简称应变仪),精度±0.2%;1m力臂(以下简称力臂),准确度误差±0.5%;扭矩传感器标定装置(以下简称标定装置);8000N·m应变式扭矩传感器(测量对象,以下简称扭矩传感器)。
1.3 测量方法
扭矩传感器标定装置按图1方式联接,当驱动电机转动时,拉压力传感器起制动作用,被测扭矩传感器所承受的扭矩通过力臂作用于拉压力传感器。仪器仪表开机预热稳定后,选定加载方向,预扭后校准零位。选定8个测量点:1000,2000,3000,4000,5000,6000,7000,8000N·m,即拉压力传感器示值分别为:1000,2000,3000,4000,5000,6000,7000,8000N,依次读取记录扭矩传感器测量应变值,计算应变系数。

图1 扭矩传感器标定装置示意图
2 数学模型
扭矩传感器应变系数:
(1)
式中:μ为扭矩传感器应变系数;F为拉压力传感器示值;L为力臂长度,1m;ε为应变仪应变值。
3 测量不确定度来源
扭矩传感器应变系数测量不确定度来源主要有:拉压力传感器示值误差、应变仪精度误差、力臂准确度误差、应变仪应变值读数误差、单次测量重复性误差。各不确定度分量列于表1。
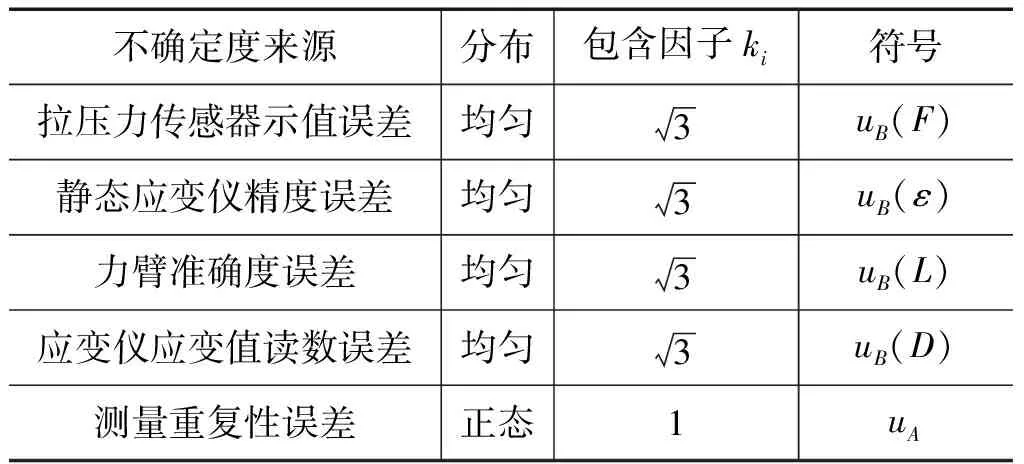
表1 不确定度分量评定预估
4 计算灵敏系数及合成标准不确定度
根据不确定度的传播率计算灵敏系数及合成标准不确定度:
c1=1;
(2)
(3)
(4)
uci= [c12uA2+c2i2uBi2(ε)+c3i2uBi2(L)+
c4i2uBi2(F)+c2i2uBi2(D)]1/2
(5)
5 标准不确定度评定
5.1 测量重复性误差引入的标准不确定度分量uA
由环境温度、人员读数等因素影响造成测量结果数据的分散采用A类方法评定。分别对8个测量点在重复性条件下进行3次独立重复测量,读取记录应变仪示值,求得传感器系数,并计算单次测量标准偏差。测量结果详见表2。

表2 测量结果
单次测量结果的实验标准差为:
(6)
测量重复性所产生的标准不确定度为:
(7)
将测量结果代入式(3)、式(4),得到实验标准差数据组详见表3。

表3 实验标准差数据组
应变值的平均值测量重复性所产生的标准不确定度为:
5.2 拉压力传感器示值误差引入的不确定度分量uB(F)
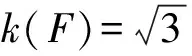
(8)
5.3 应变仪精度误差引入的不确定度分量uB(ε)

(9)
5.4 力臂引入的不确定度分量uB(L)的评定

5.5 应变仪应变值读数误差引入的不确定度分量uB(D)
由于本次测量所用应变仪是数显仪表,且由同一人进行多次重复测量评定,因此本次测量由应变仪应变值读数误差引起的不确定度分量uB(D)可以忽略不计,即uB(D)=0。
根据式(8)、式(9)计算出各不确定度分量数值详见表4。

表4 各不确定度分量数值
6 扭矩传感器应变系数μ的合成标准不确定度uc
根据式(2)、(3)、(4)计算得出灵敏系数,将表4中各不确定度分量评定结果代入式(5)计算,得到合成不确定度结果详见表5。

表5 合成不确定度结果
7 扭矩传感器应变系数μ的扩展不确定度U及相对测量不确定度U95rel
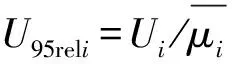
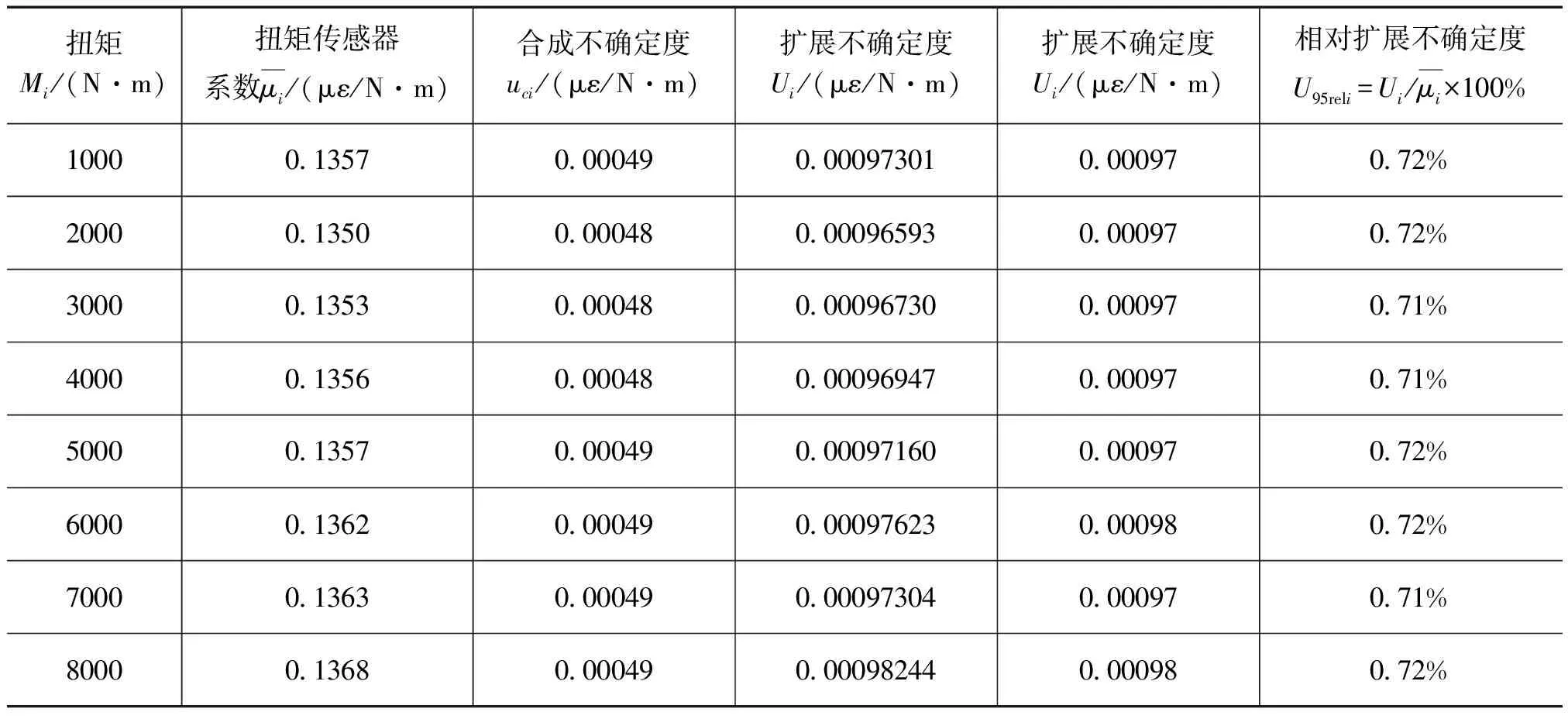
表6 扩展不确定度结果
8 结论
从评定结果来看,8个测量点处测量结果的扩展不确定度Ui及相对扩展不确定度U95reli基本一致,该扭矩传感器本次测量中整个量程范围内的不确定度分布均匀,取其均值得出该扭矩传感器在整个量程范围内测量结果的扩展不确定度U为0.00097με/N·m,相对扩展不确定度U95rel为0.72%。
[1] JJF 1059.1—2012测量不确定度评定与表示
[2] 上海市计量测试技术研究院编.常用测量不确定度评定方法及应用实例. 中国计量出版社,2000
[3] 唐胜睦.测量不确定度评定中灵敏系数的计算. 计量与测试技术,2013,40(1)
[4] 王丹,林中.扭矩传感器测量结果不确定度的评定. 中国计量,2006(12)
[5] 闫立新,等.利用Excel编制测量不确定度计算表格的方法与使用. 计量技术,2014(2)
10.3969/j.issn.1000-0771.2015.12.23
