基于参数估计的相位噪声检测方法

2015-06-09张亦弛赵建军

计量技术 2015年12期

关键词：参数估计遗传算法噪声

张亦弛赵建军桂周龚伟

(1.海军航空工程学院研究生管理大队，烟台 264001； 2.海军航空工程学院兵器科学与技术系，烟台 264001)

基于参数估计的相位噪声检测方法

张亦弛1赵建军2桂周1龚伟1

(1.海军航空工程学院研究生管理大队，烟台 264001； 2.海军航空工程学院兵器科学与技术系，烟台 264001)

本文对传统鉴相法提取相位噪声信号进行了改进处理，提出了一种基于遗传算法的参数估计方法，来减小频差相位差对相位噪声测量的影响，提高系统检测精度。仿真结果表明该算法能够更加精确地提取和测量实测信号的相位噪声，减小测量中的误差。

鉴相法；相位噪声；遗传算法；参数估计；提取噪声

0 引言

现代海战中，性能不断提高的反舰导弹和空战的飞机已成为了水面舰艇的主要威胁，对空防御成为了水面舰艇的主要任务之一。舰空导弹武器系统正是适应这种防空的需求在不断地发展，能够使导弹精确打击来袭目标成为了我们重要的研究目标。照射器是舰空导弹武器系统一个重要的组成部分，不断地发出连续波信号照射来袭目标，为舰空导弹的发射和跟踪提供指示。因此，在执行任务之前，必须对照射器信号参数进行检测。目前，对照射器信号参数检测的主要手段是对照射器频率源相位噪声的测量，而鉴相法是最常采用的测量方法。

本文针对传统鉴相法提取相位噪声信号存在的不足，提出一种基于遗传算法的参数估计算法，减小频率差相位差对测量结果的影响，提高测量相位噪声信号的精度。

1 相位噪声的定义及测量方法

相位噪声一般是指在系统内各种噪声作用下引起的输出信号相位的随机起伏。通常定义为在某一给定偏移频率处单位带宽内的信号功率与信号的总功率比值。相位噪声是一项非常重要的性能指标，从频域看它分布在载波信号两旁按幂律谱分布。它对雷达系统的影响很大，相位噪声过高会严重影响雷达系统中目标的分辨能力，因此，要精确测量信号中相位噪声并对系统进行标校。

频率源相位噪声的测量方法多种多样，具体选用哪一种测量方法应从测量动态范围的大小、测试精度的要求、测量成本的多少、测量设备的可用性等多个方便进行考虑。相位噪声测量方法可以分为时域测量和频域测量方法。在时域测量方法中有直接计数法、差拍计数法等方法；频域测量方法有频谱仪直接测量法、差拍法、鉴频法和正交鉴相法等。为了追求测试的高精确度，本文中采取锁相正交式鉴相法进行测量相位噪声，正交鉴相法测量相位噪声时，良好的正交性可以保证相位灵敏度最大和调幅灵敏度最小。

鉴相法是目前最常采用测试方法，具有灵敏度最高、系统本底噪声最低、分析范围广、工作频率宽等特点，而且具有调幅抑制功能。测试系统中，采用双平衡混频器作为鉴相器[1]。其测量过程是将参考信号源调到与被测信号源的输出信号相同的频率，相位噪声测试系统自动调节参考信号的相位保持与被测信号正交，然后分别将被测信号和参考信号加到鉴相器两端进行鉴相，鉴相后的信号通过低通滤波器滤除高频部分，再经过低噪声放大器，最终得到的是一个相位差信号，利用相位噪声测试仪对此信号进行频谱分析，可以提取出相位噪声，本文采用PN9000相位噪声测试仪。锁相正交式鉴相法测噪原理如图1所示。

图1 锁相正交式鉴相法测噪原理

2 相位噪声信号的建模

2.1 理想情况下相位噪声信号的建模

设被测信号：

vi(t)=Ai[1+a(t)]sin[2pf0t+θ0+φ0(t)]

(1)

式中，a(t)为被测信号的幅度噪声；φ0(t)为被测信号的相位噪声；f0和θ0分别为被测信号源的频率和初始相位。因为相位测试系统的双平衡混频器对寄生调幅有较强的抑制能力，所以，被测信号的寄生调幅可以忽略[2]，故上式可变为：

vi(t)=Aisin[2pf0t+θ0+φ0(t)]

(2)

参考源在相位正交的时候进入锁相状态，锁定低噪参考信号，对被测信号源的相位波动进行鉴相，故参考源信号表示为：

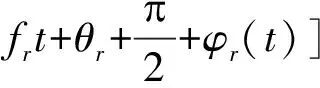
(3)

选取参考源时要注意参考信号相位噪声要比被测源相位噪声低10dB以上，所以，参考源的相位噪声起伏可忽略。

当上述条件成立时，双平衡混频器的输出电压的起伏就是被测信号的相位起伏引起的[3]。经过鉴相器后输出电压表示为：

vo(t) =vr(t)×vi(t)

φr(t)+sin[2p (f0-fr)t+θ0-θr+

φ0(t)-φr(t)]}

(4)

经LPF滤波后输出信号为：

φ0(t)-φr(t)]

=Ksin[Δwt+Δθ+φ(t)]

(5)

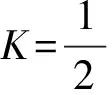
在实际测试中，信号经过低噪放大器后还可能会有带有直流分量。设此时该信号为y(t)，则：

y(t)=Ksin[Δwt+Δθ+φ(t)]+C

(6)

式中，C为直流分量。由于测试系统是基于理想的情况下的，所以，有Δw=0，Δθ=0，φ(t)≫1和sin[φ(t)]≈φ(t)。于是近似的认为y(t)=Kφ(t)+C，所以，相位噪声信号φ(t)的功率谱密度可以通过经过低噪声放大器的输出信号y(t)的功率谱密度而求得。

3.2 实际测试下相位噪声信号的建模

理想情况下提取相位噪声信号时，频率差Δw=0，初始相位差Δθ=0。然而，在实际的测试过程中，所有测试设备都存在一定的误差，频率差和初始相位差虽然接近为0，但是不等于0。因此，分析相位噪声信号时，忽略频率差和初始相位差这两个参数对最终的相位噪声信号测量精度是有影响的。在提取相位噪声信号时，为了高精度地测量相位噪声信号，应该考虑到频差和初始相位差对测量结果的影响。

根据式(6)，经过低噪声放大器的输出信号：

y(t)=Ksin(Δwt+Δθ+φ(t))+C

≈Ksin(Δwt+Δθ)+Kcos(Δwt+

Δθ)φ(t)+C

(7)

于是相位噪声信号可表示为[4]：

(8)

在实际的测量中，如果我们能够测得上式中的K、Δw、Δθ和C这几个参数的值，那么相位噪声信号的大小就可以测量得到。

3 基于遗传算法的信号参数估计

遗传算法是模拟生物进化机制发展起来的全局搜索和优化方法，通过模仿自然界的选择与遗传的机理来寻找最优解。遗传算法是一类全局收敛算法，因而能够精确地估计正弦信号的特征参数[5]。

3.1 基于遗传算法的正弦信号参数估计

假设正弦波信号的表达式为：

x(t)=Asin(2p ft+φ)+C

(9)

式中，A为信号的幅度；f为频率；φ为初始相位角；C为直流分量。

对于正弦信号x(t)，实际采集到的是实验信号的波形。而具体参数估计中所用到的是所得波形的有限时域采样数据，即一个个采样数值对：(x1,y1),(x2,y2),…,(xn,yn)。令θ=[A,f,φ,C]T，则θ为待估参数；ε(t)为随机误差，信号采样第i次样本值与样本估计值的偏差表示为：

(10)

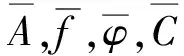
(11)

定义目标函数

G(θ)=min[εi(θ)](i=1,2,…,n)

(12)

式中，使G(θ)极小化的θ即为待估计的正弦波信号特征参数。

本文采用实数值编码的遗传算法对正弦波信号参数进行估计。适应度函数必须满足单值、连续、非负和最大化等条件[6]，目标函数为G(θ)，所以，选择F=1/G(θ)作为适应度函数。利用遗传算法对该问题进行求解，遗传算法采纳了自然进化模型，经过编码、选择、交叉、编译和解码等步骤。这个过程将导致群种像自然进化一样的后代比前代更加适应环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

3.2 基于遗传算法的频差相位差消除

遗传算法可以精确地对特征参数进行估计，寻找到最优解。利用上述方法，根据信号的时域采样值，可以估计出经过低噪声放大器的输出信号y(t)中的几个特征参数：信号幅度A、频率差Δw、初始相位差Δθ以及直流分量C。

而根据式(8)得知提取到的相位噪声信号为：

经过遗传算法对时域采样后的信号进行特征参数估计，得到一组使适应度函数G(θ)极小化的θ，θ=[A,f,φ,C]T。将得到的正弦波信号特征参数代入上式，再对信号φ(t)进行功率谱估计，就能估计出信号相位噪声信号大小。相位噪声测试具体方法如图2所示。

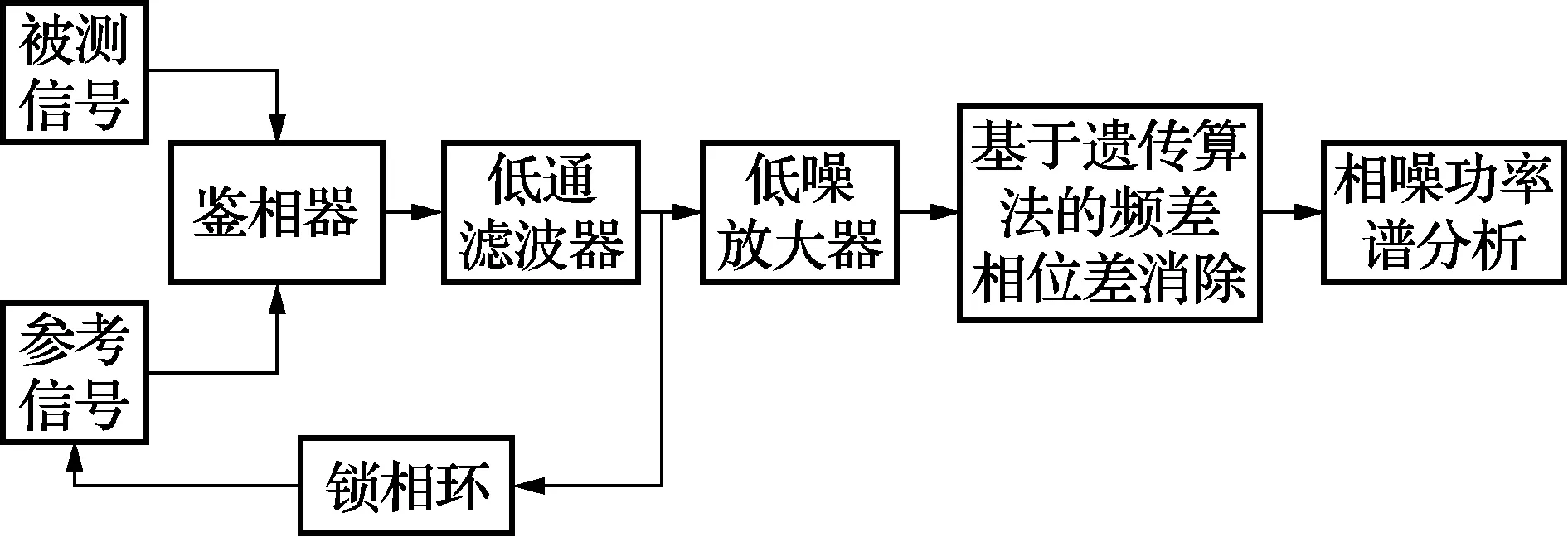
图2 基于遗传算法的频差相位差消除的相噪检测

4 仿真结果与分析

为验证文中参数估计算法能否有效消除频率差、初始相位差等参数对测量结果的影响，我们用Matlab软件对相位噪声信号的提取进行仿真。仿真信号为经过低噪放大器的输出信号y(t)。实验方案采取比对实验，仿真实验的方案如图3所示。

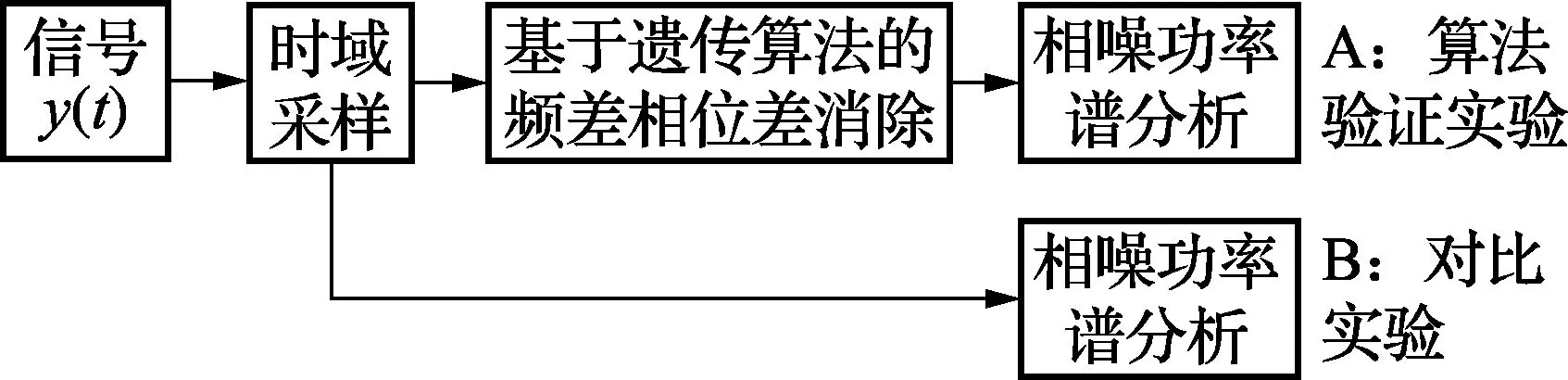
图3 仿真实验方案

仿真实验中，低噪放大器的输出信号为：

y(t)=Asin(Δwt+Δθ+φ(t))+C

其中，A=3，Δw=0.1rad/s，Δθ=0.08rad，C=1。相位噪声信号φ(t)是由rand(t)/5产生的均匀分布的伪随机信号序列。采样频率f=50Hz，一共采样10000个数据[7]。经过时域采样后的信号如图4所示。

图4 时域采样得到的信号

采样信号经过遗传算法进行参数估计，用户只需要给出目标函数与采样数据，利用Matlab中遗传函数工具箱运行即可观测结果，目标函数如下[8]：

function F=fitness(x)

t=0:0.02:200;r=rand(1,10001)/5;

y=3*sin(0.21*t+0.128+r)+1;

espi=zeros(1,10001);

for i=1:10001

espi(i)=abs(y(i)-x(1)*sin(x(2)*t(i)+x(3)+r(i))-x(4));

end

espi=sort(espi);

F=espi(10001);

end

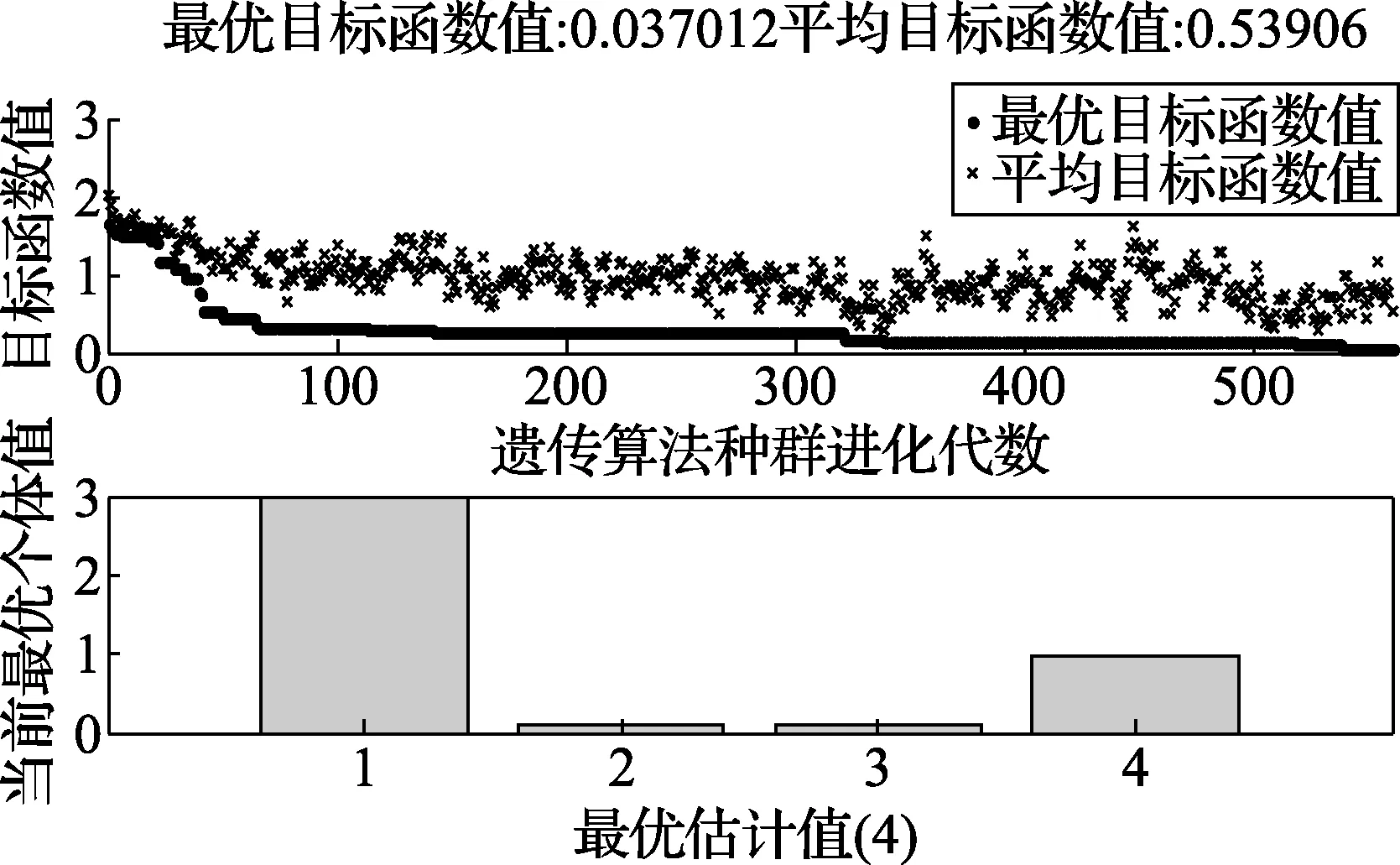
图5 经过470次迭代后的运行结果

图5中，下图4个参数分别代表信号y(t)的幅度、频率、初始相位差和直流分量的最优估计值。从结果可以看出，最优个体产生在第137代，结果是θ=[2.996,0.1,0.086,0.998]T，此个体对应的目标函数值为0.031334。可以看出，此结果与理想信号y(t)非常吻合，遗传算法在提取正弦函数参数上效果较好。

算法验证实验是按照仿真方案A来进行的，经过遗传算法进行参数估计，得到信号y(t)的参数估计值θ=[2.996,0.1,0.086,0.998]T，然后根据参数估计值进行相位噪声信号的提取，对相位噪声信号进行功率谱密度分析。作为算法验证实验的对比实验，其实验流程如仿真方案B所示，采样后得到的数据直接根据传统鉴相法提取相位噪声的方法提取相噪信号，然后进行功率谱密度分析，提取相位噪声过程中忽略了频率差、相位差等参数对测量结果的影响。参考测试是对仿真信号中设定的相位噪声信号φ(t)直接进行功率谱密度计算，所测试得到的结果可以作为一个标准值，对比分析实验A和B测量结果的精度。通过仿真得到的相位噪声信号功率谱密度如图6所示。

图6中，横坐标为噪声偏离载波频率的远近(0.01～25Hz)，纵坐标为相应噪声波动的谱密度(-50～50dBc/Hz)。对比图6中测得的相位噪声信号功率谱，分析实验A和实验B测得的相位噪声信号大小，计算两种方法所得测量值的均方误差MSE值和平均误差[10]，如表1所示:

图6 相位噪声信号功率谱

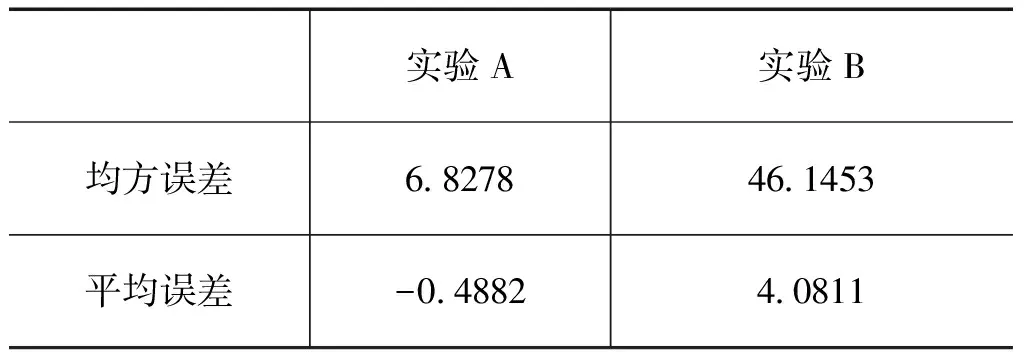
表1 测量值误差对比

从表1可以看出，实验A的测量值的均方误差和平均误差明显低于实验B，而且从图6中也能看出实验A所得相噪功率谱图像更加接近标准功率谱图像。所以可以得出结论：经过参数估计测量得到的相位噪声信号大小明显更加接近参考测试得到的标准相位噪声信号。由图3实验方案可知，算法验证实验和对比实验采用的相位噪声功率谱密度方法一样，而且测量条件相同，其唯一的不同点是算法验证实验采用了遗传算法对频差相位差等参数进行估计，然后根据估计得到的参数提取相位噪声信号。说明文中所述的基于遗传算法的消除频率差相位差的参数估计方法确实能够有效提高相位噪声测量精度。