基于支持向量机的油水界面预测
2015-06-09李建荣
李建荣
(胜利油田现河采油厂,东营 257068)
基于支持向量机的油水界面预测
李建荣
(胜利油田现河采油厂,东营 257068)
针对原油储油罐油水界面检测时影响因素多、数据维数大,非线性等难以处理的问题,作者提出基于粒子群优化算法和支持向量机相结合的油水界面预测方法。通过对油罐实测数据的计算仿真,经过寻优进一步优化模型,得到油水界面的预测结果并生成了拟合效果图。分析误差表明该预测方法精度高、误差小,可以较好地实现储油罐油水界面的测量。
油罐计量;油水界面预测;粒子群优化算法;支持向量机
0 引言
目前,我国石化企业均按ISO 3170(GB/T 4756—1998)《石油液体产品手工取样法》采样,其采样的准确度及难度受诸多因素的影响,且操作者劳动强度大,更不利于安全生产。随着科学技术的发展和石化企业自动化水平的提高,为适应现代技术的要求,沿用几十年的石油液体产品手工取样被自动化设备取代是发展趋势。要实现自动化取样,了解油罐中水层的高度和原油的含水率,随时掌握油罐中原油的精确储量,就要实现对油水界面的自动化定位,而实现油水界面自动化定位最关键的技术就是能够对油水两相流中的含水率进行测量与预测。对于含水率的测量,主要有射线法、超声法、层析法、电容法、电导法、微波法[1-4]等,但在对于已知数据处理上的方法却相对较少,究其原因,主要是由于油水两相流的影响因素较多[5],得到的数据维数高,处理不方便。
SVM是在统计学习理论的基础上提出的机器学习工具,它遵循结构风险最小化(Structural Risk Minimization,SRM)原理,能较好的处理小样本、高维数和非线性等问题[6],在模式识别、分类和数据预测、拟合方面得到了广泛应用。粒子群算法(PSO)是根据鸟群觅食行为提出的一种全局智能仿生方法,具有收敛快、人为设定参数少、并行实施、易编程实现等优点[7]。本文尝试将支持向量机运用到油水界面含水率的预测中,并通过PSO算法来实现对支持向量机核函数和惩罚因子[8]的优化。
1 基于PSO-SVM的油水含水率预测
1.1 支持向量机的原理和实现
把支持向量机估计指示函数中得到的结论推广到实函数中,即支持向量机回归[9]。根据统计学习理论,构造线性回归方程[10]
f(x)=ωΦ(x)+b
(1)
式中,非线性映射φ把数据映射到高维特征空间;ω为在空间中的特征向量;b为偏置值。

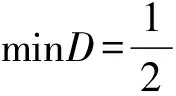

(2)
式中,ε为不敏感损失函数;C为惩罚系数。
引入拉格朗日函数和对偶变量:
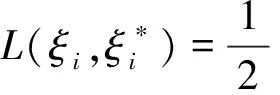
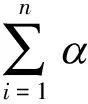
(3)
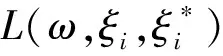

i=1,2,…,n
(4)

(5)

(6)
于是可得

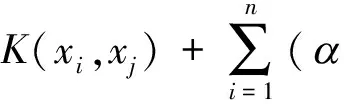
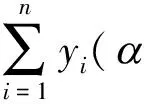
(7)

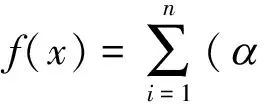
(8)
1.2 粒子群优化算法
粒子群优化算法是由Kennedy和Eberhart提出的一种基于群智能(Swarm Intelligence)的演化计算技术,是在鸟群、鱼群和人类社会的行为规律的启发下提出来的粒子群优化算法通过群体中的粒子间的合作与竞争产生的群体智能来指导优化搜索。与演化计算相比,粒子群算法保留了基于种群的全局搜索策略,它采用的速度-位移模型操作简单,避免了复杂的遗传操作。粒子群优化算法特有的记忆,使其可以动态跟踪当前的搜索情况,调整其搜索策略。与演化计算相比,粒子群优化算法是一种高效的并行搜索算法。由于算法收敛速度快,设置参数少,近年来受到学术界的广泛重视[11]。
粒子群优化算法的精确描述为:在D维目标搜索空间中,n个粒子组成一个群落,每个粒子i包含一个D维的位置向量xi=(xi1,xi2,…,xiD)和速度向量vi=(vi1,vi2,…,viD)。粒子i在搜索D维解空间时,记住其搜索到的最优位置pi。在每次迭代中,粒子i根据自身惯性、自身经验pi=(pi1,pi2,…,piD)和粒子群最优经验pg=(pg1,pg2,…,pgD)调整自身的速度向量,进而调整自身位置。可以通过一个适应值函数f(x)来衡量粒子的优势。
1.3 粒子群优化支持向量机
利用粒子群算法优化支持向量机的算法如下:
Step 1确定适应度函数f(x);
Step 2初始化种群的位置,数量以及速度;
Step 3适应度定标;
Step 4是否满足停止条件?否,前往step 5;是,前往step 7
Step 5速度更新和位置更新
Step6利用更新的数据计算适用度,前往step 4;
Step 7利用输出的最优解优化支持向量机模型,并对数据进行拟合。
2 基于粒子群优化的支持向量机仿真实例
2.1 数据的获取
针对某一油罐,对其进行不同高度的取样,分别测得其液位高度、出罐压力、温度、质量流量、混合密度、体积流量,进罐压力、以及含水率等数据为训练样本来训练PSO-SVM模型。取样测量装置示意图如图1所示。

图1 测量装置
通过定位模块将吸油口定位到指定位置,油水二相流进入取样管,含水率测量仪获得含水率的数据,并进行记录,与此同时,记录其出罐压力、罐内温度等数据。得到84个不同取样口高度的数据,其中的22个数据如表1所示。
2.2 仿真过程
将支持向量机的条件限定在[0,100],通过粒子群算法进行寻优,得到适用度和迭代数之间的关系,其中bestc=100,bestg=24.6184。交叉检验时的三维图如图2所示。

表1 取样数据
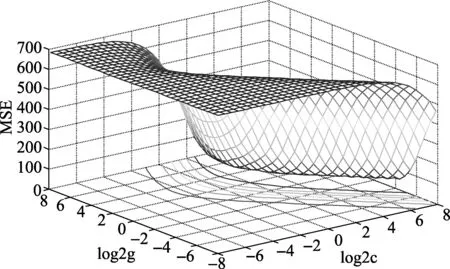
图2 交叉检验时的三维图
利用寻优得到的结果,来训练支持向量机模型,并利用得到的模型来预测得到的数据,拟合效果如图3。

图3 拟合效果图
3 结果分析
通过PSO优化支持向量机参数,并对含水率进行预测,对数据拟合效果较好,误差均不超过5%。支持向量机是可以作为预测含水率的新方法。
4 结论
由于油水两相流是个非线性关系,而且影响因素较多,数据的维数相对较大,而支持向量机在处理大维数数据方面有独特的优势,本文以油罐中实测数据为实例,对油水二相流含水率运用支持向量机进行拟合,拟合误差较小,预测精度较高。
[1] 李霞,黄志尧,王保良.应用单相流量计测量油水两相流[J].工程热物理学报,2008,29 ( 11 ) :1872-1874
[2] 张修刚,王栋,林宗虎.近期多相流过程层析成像技术的发展[J].热能动力工程, 2004, 19( 3) : 221-226
[3] JORGE L G O,JuLIO C P,RUUD V,et al. Mass flow rate measurements in gas-liquid flows by means of a venture or orifice plate coupled to a void fraction sensor[J].Experimental Thermal and Fluid Science,2009,33:253-260
[4] 王超,王玉琳,张文彪.基于静电传感的气固两相流测量及研究装置[J].电子测量与仪器学报,2011,25( 1) : 1-9
[5] 田晶京.无网格方法在油罐计量系统中的应用研究[J]. 计量技术,2012(3):26-27
[6] VAPNIK V N. An overview of statistical learning theory[J]. Neural Networks,IEEE Transactions,1999,10(5):988-999
[7] 徐飞,岩石力学性态预测的PSO-SVM模型[J]. 岩石力学与工程学报,2009,28(2):3699-3704
[8] 姜谙男. 基于PSO-SVM非线性时序模型的隧洞围岩变形预报[J]. 岩土力学,2007,28(6):1176-1180
[9] 王定成. 支持向量机建模预测与控制[M].北京:气象出版社,2009:20-27
[10] Vapnik V. The Nature of Science Learning Theory[M]. New York:Springer,1999
[11] 段晓东,刘向东.粒子群算法及其应用[M].沈阳:辽宁大学出版社,2007:29-34
10.3969/j.issn.1000-0771.2015.12.08
