单层屈曲约束支撑框架的抗震参数

冯玉龙 吴 京 孟少平 付 康

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)



单层屈曲约束支撑框架的抗震参数

冯玉龙 吴 京 孟少平 付 康

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)

为了给屈曲约束支撑框架设计提供参考,对单层屈曲约束支撑框架的抗震参数进行了研究．通过结构侧移分析,推导出表征该结构体系受力和变形特性的3个关键参数:支撑-框架刚度比、支撑-框架屈服强度比和梁-柱线刚度比．以特定地震动下结构最大位移和残余位移作为评价指标,对结构进行了参数化分析.分析结果表明:当支撑-框架刚度比和梁-柱线刚度比较小时,增大刚度比可以明显减小结构位移;支撑-框架屈服强度比主要对结构的屈服位移和机制影响较大;支撑-框架刚度比、支撑-框架屈服强度比和梁-柱线刚度比的合理值分别为2,0.7和0.45～5.00．据此设计了2个单层算例,并进行了抗震性能分析.结果表明:在结构中,形成了支撑-梁-柱屈服机制;当支撑屈服后,框架承担的剪力比逐渐增大;支撑布置方式对结构顶点位移响应基本无影响,对相邻柱的轴力影响则较大．

单层屈曲约束支撑框架;抗震参数;合理参数值;布置方式

屈曲约束支撑(BRB)在受拉和受压时都可屈服而不屈曲,具有稳定的滞回耗能能力和较大的延性,克服了传统支撑受压易失稳的缺点[1]．它与抗弯框架结合形成了屈曲约束支撑框架(BRBF)结构体系,目前广泛应用于工程结构中[2-3]．

近30年来,国内外学者对多高层BRBF结构体系进行了大量理论和试验研究．文献[4-6]通过对比分析指出,BRB作为耗能减震装置,能够起到小震中提供较大刚度、大震中保护主体结构的作用．美国规范[7]和我国规范[8]中增加了BRBF部分内容,主要包括BRB结构设计原则、BRB构件及其连接的设计与加工．

为了给多高层BRBF结构抗震初步设计提供指导、寻求结构性能和经济效益的平衡点,学者们开始研究结构体系刚度和强度等抗震参数及BRB在框架中的布置方式．Kim等[9]发现BRB的截面面积和屈服强度对结构抗震性能影响较大;贾明明等[10]指出对BRB钢框架进行设计时,宜采用基于支撑-框架刚度比布置支撑的方法;赵瑛等[11]建立了BRBF在大震下的层间位移角最大值随侧向刚度比k变化的关系曲线,获得了k的合理取值范围．上述研究主要针对多高层BRBF结构体系展开．然而,对于多高层BRBF结构体系, BRB截面面积、BRB屈服强度、支撑-框架刚度比3个参数沿楼层方向变化对结构抗震性能影响的规律较复杂,难以全面表征多高层BRBF结构体系的动静力特性．

多高层结构属于多自由度体系,性能参数多变,设计过程复杂．等效单自由度体系研究是多自由度体系抗震计算和设计的基础．为此,本文首先推导了表征单层BRBF结构体系受力和变形特性的关键参数．在此基础上,通过参数化分析得到单层BRBF结构体系参数的合理值．最后,通过算例分析了合理参数值下单层BRBF的抗震性能．

1 结构体系参数确定

图1为单层单跨BRBF结构侧移分析简图．图中,u为顶点位移;F为侧向力;H和L分别为结构的层高和跨度;Ib和Ic分别为框架梁和柱的截面惯性矩;Abrb为BRB核心板截面面积;E为钢材弹性模量;θ为支撑与水平方向的夹角．

图1 结构侧移分析简图

结构抗侧力体系由抗弯框架和单斜撑BRB组成,BRBF的侧向刚度K可以等效为框架侧向刚度Kf和BRB提供的侧向刚度Kbrb之和,即

K=Kbrb+Kf=Kf(1+S)

(1)

式中,S=Kbrb/Kf为支撑-框架刚度比．在以整体呈现剪切变形为主的BRBF结构中,有

(2)

(3)

式中,ρ=ib/ic为梁-柱线刚度比,其中ib和ic分别为框架梁和柱的线刚度．

由式(3)可知,在结构高度、弹性模量和支撑夹角确定的条件下,支撑侧向刚度与面积成正比．假定支撑初始侧向刚度大于框架初始侧向刚度,并且支撑屈服位移小于框架屈服位移,根据式(1)可以绘制出BRBF结构侧向力F与顶点位移u的关系曲线,结果见图2．图中,α,β分别为支撑和框架屈服后刚度与其初始刚度之比;uy,brb,uy,f分别为BRB和框架的屈服位移;um为结构的最大位移．

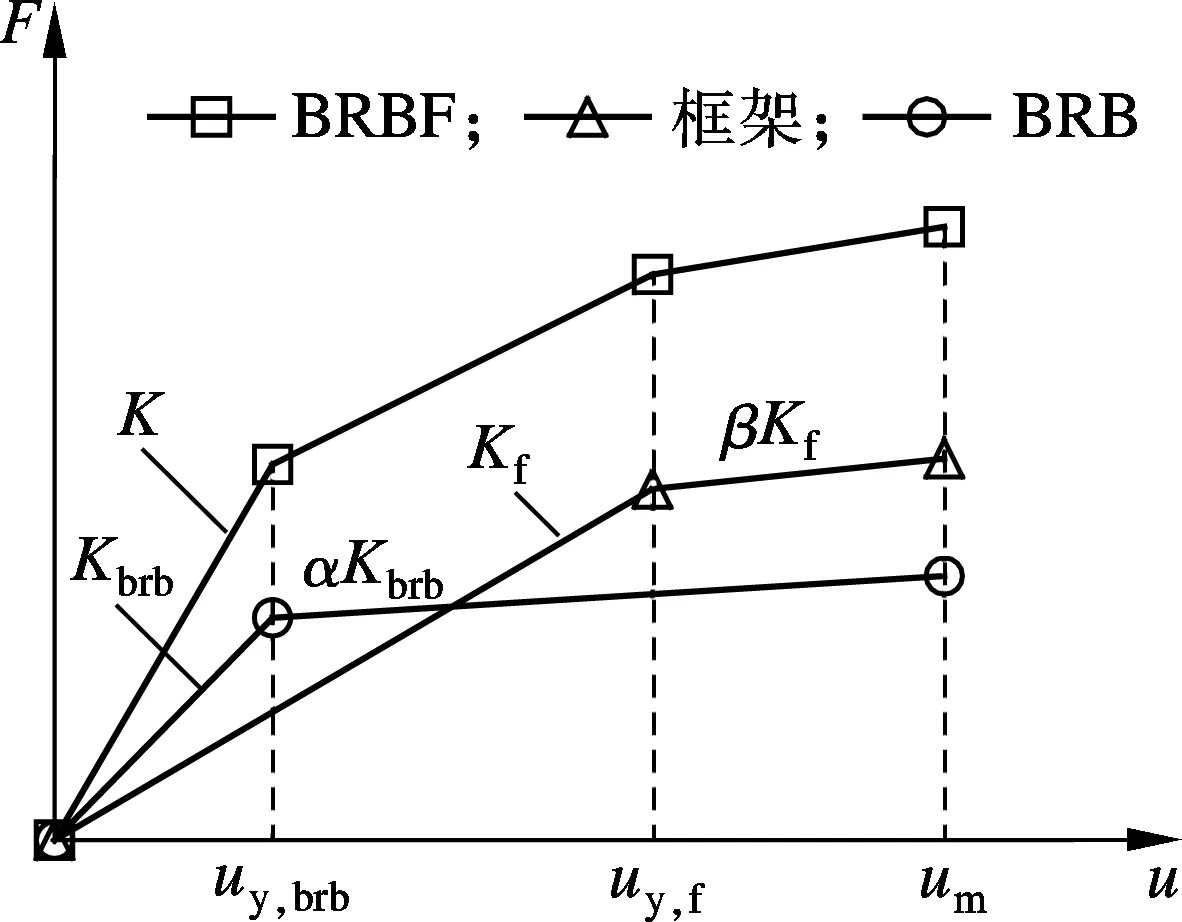
图2 结构侧向力-位移曲线

支撑屈服时的层间位移角θy,brb为

(4)

式中,fy,brb为BRB核心板的屈服强度．

由式(4)可见,支撑屈服层间位移角主要与其自身屈服强度有关,与截面面积无关．当θ=45°,fy,brb=210 MPa,E=206 GPa时,θy,brb≈1/490．规范[12]规定多高层钢结构的弹性层间位移角限值为1/250．因此,支撑先于框架屈服的条件容易满足．定义参数D为支撑-框架的屈服强度比,即D=fy,brb/fy,f,其中fy,f为框架梁柱的屈服强度;D决定了结构的屈服位移及结构构件的屈服顺序．

2 模型分析

2.1 数值模型

采用Opensees数值模拟软件对结构进行非线性分析(包括静力推覆分析和动力时程分析)．梁柱构件使用基于柔度法的非线性梁柱单元,材料采用双线性模型;BRB使用桁架单元,材料采用Giuffre-Menegotto-Pinto模型．梁柱和支撑的屈服后刚度比均设置为0.025．结构质量集中在2个顶点上,所有分析均考虑重力二阶效应．时程分析采用El Centro地震波,加速度峰值调整至400 cm/s2．

2.2 参数化分析工况

对单层单跨BRB钢框架进行初步设计,层高和跨度均为5 m,结构简图同图1．钢材弹性模量为206 GPa,每侧顶点附加质量为66 t．假定S=2,D=0.7,ρ=0.45;梁为H型钢,截面高度和宽度分别为250和150 mm;腹板和翼缘厚度分别为6和8 mm;柱为方钢管,截面高度为250 mm,壁厚10 mm;框架梁柱屈服强度为345 MPa．据此可以设计出BRB的截面面积和屈服强度分别为277 mm2和235 MPa．

为了能进一步了解3个抗震参数对单层BRBF地震反应的影响并确定最合理的参数值,下面对结构进行参数化分析．采用保持2个参数不变、仅改变1个参数的原则,制定了4种参数化分析工况(见表1～表4)．

表1 工况1

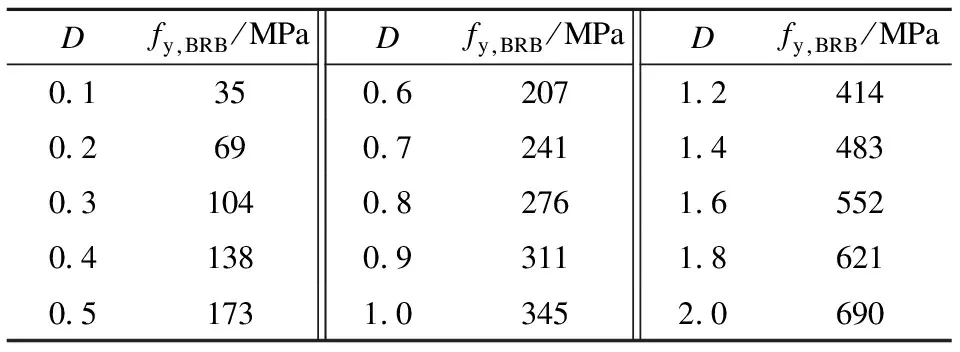
表2 工况2

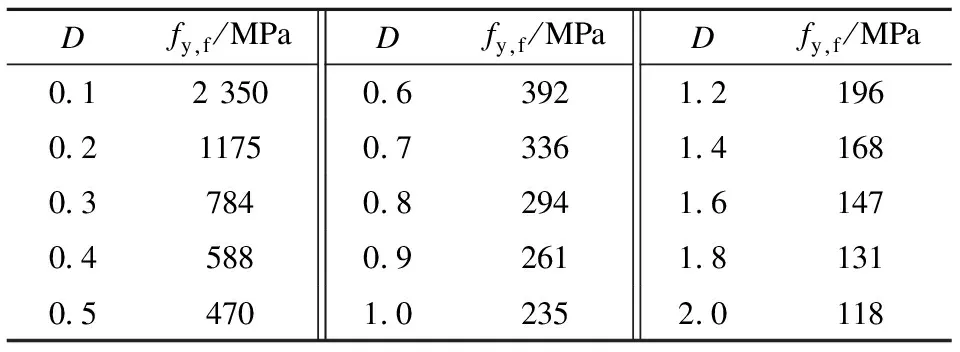
表3 工况3

表4 工况4

注:梁截面尺寸为高度×宽度×腹板厚度×翼缘厚度．

3 参数化分析结果

3.1 支撑-框架刚度比

由式(1)可得结构周期T和支撑-框架刚度比S的关系为

(5)

式中,M为结构总质量．

由图3可知,结构周期T随着刚度比S的减小而单调减小．当S较小时,支撑面积对刚度影响较大;当S>6时,支撑面积对刚度影响较小．周期理论值和OpenSees模拟结果较接近,由此证明了数值模拟的正确性．

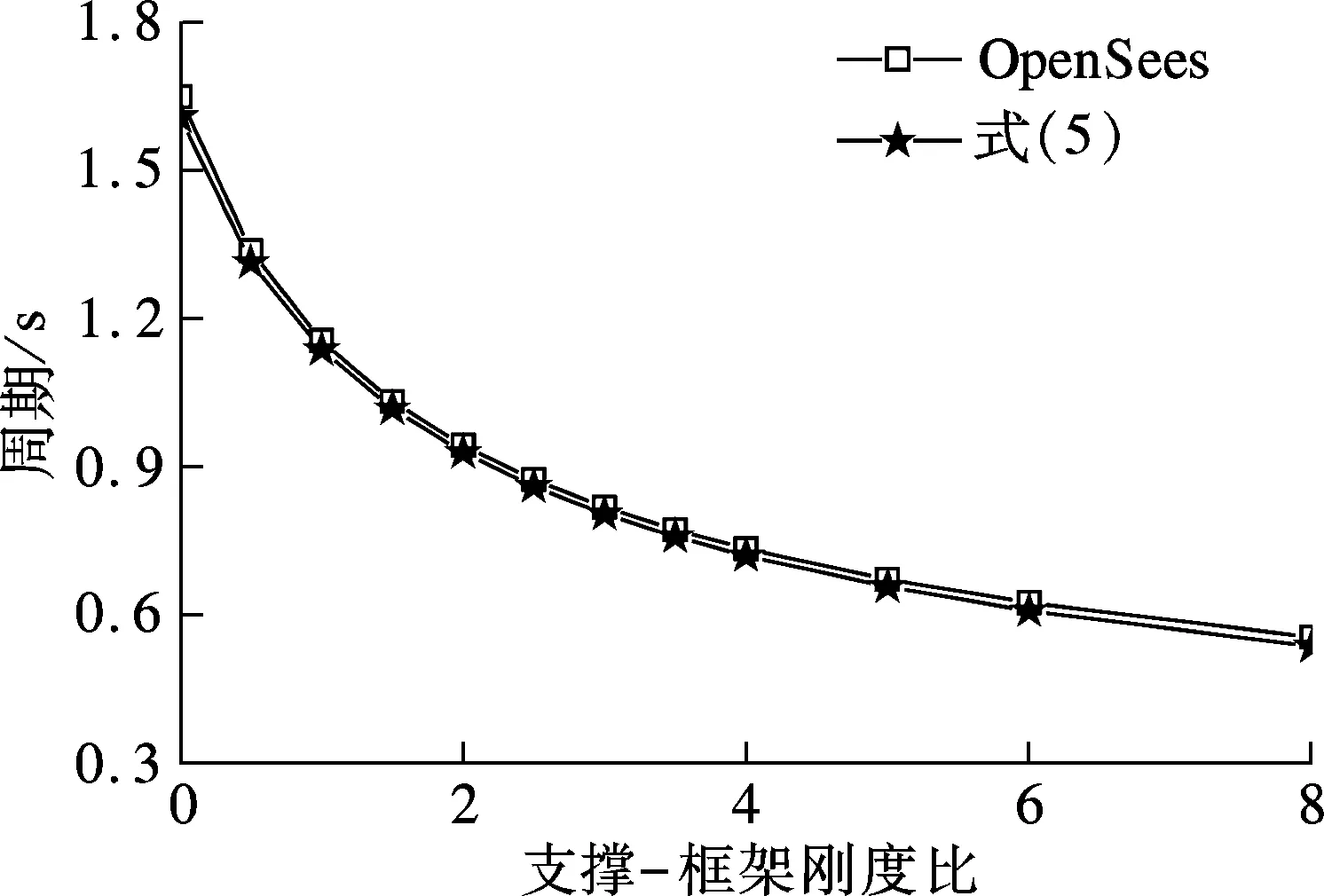
图3 周期和支撑-框架刚度比的关系曲线

图4(a)为工况1下结构的侧向力F与顶点位移u的关系曲线(即推覆曲线)．图中,区域Ⅰ内BRB和框架均保持弹性,S越大则结构的刚度越大;区域Ⅱ内BRB屈服,框架保持弹性,S取值不同时对应结构的力位移曲线几乎平行,说明BRB屈服后结构刚度主要由框架提供;区域Ⅲ内BRB和框架共同屈服,结构接近倒塌状态．BRB在区域Ⅰ与区域Ⅱ的界限处屈服,框架在区域Ⅱ与区域Ⅲ的界限处屈服．在结构推覆曲线上,BRB和框架屈服时对应的位置分别称为BRBF的第一屈服点和第二屈服点．S取值不同时对应结构的第一屈服点和第二屈服点均相同,说明结构屈服位移主要与构件屈服强度有关,与构件截面无关．

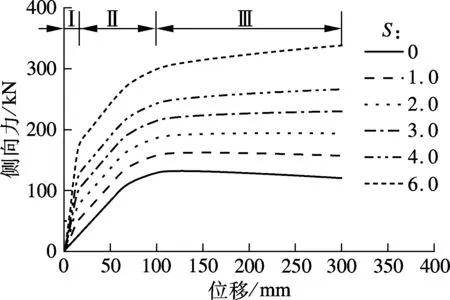
(a) 工况1

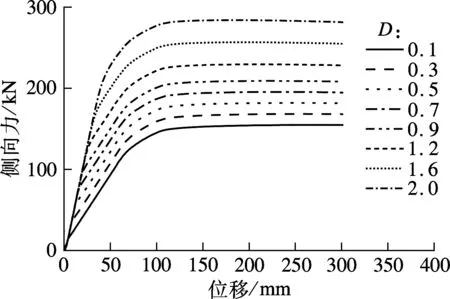
(b) 工况2

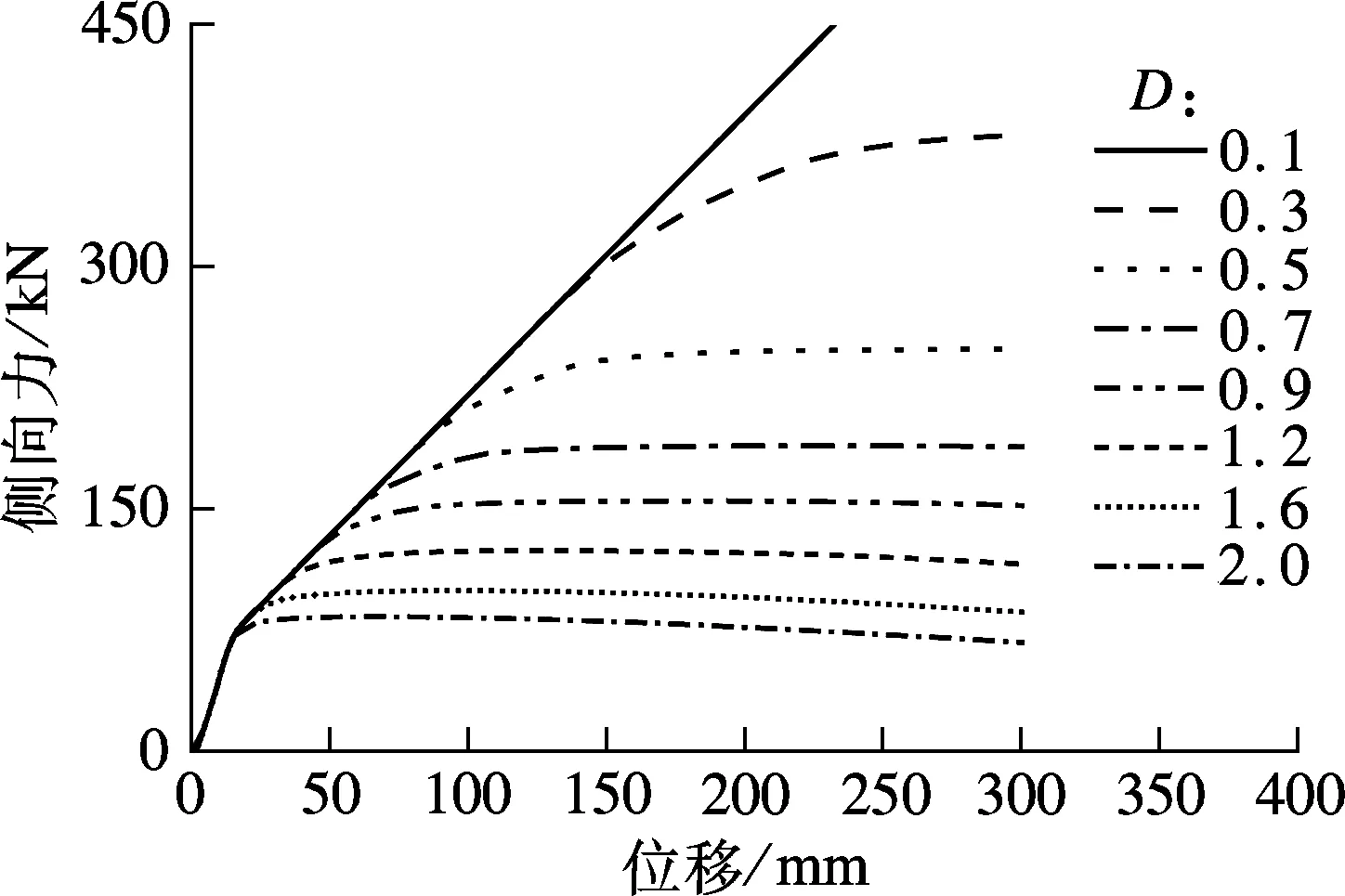
(c) 工况3

图5为工况1下S取值不同时对应结构的顶点位移时程曲线．由图可知,S越小则结构顶点位移响应越大,残余位移相应也越大．当S=0(即结构为纯框架)时,地震动作用下结构呈现出明显的塑性．图6为工况1下S取值不同时对应结构的位移和支撑-框架刚度比关系曲线．由图可知,当S>2时,提高刚度比S对减小最大位移和残余位移效果并不明显．因此,S的合理值为2．

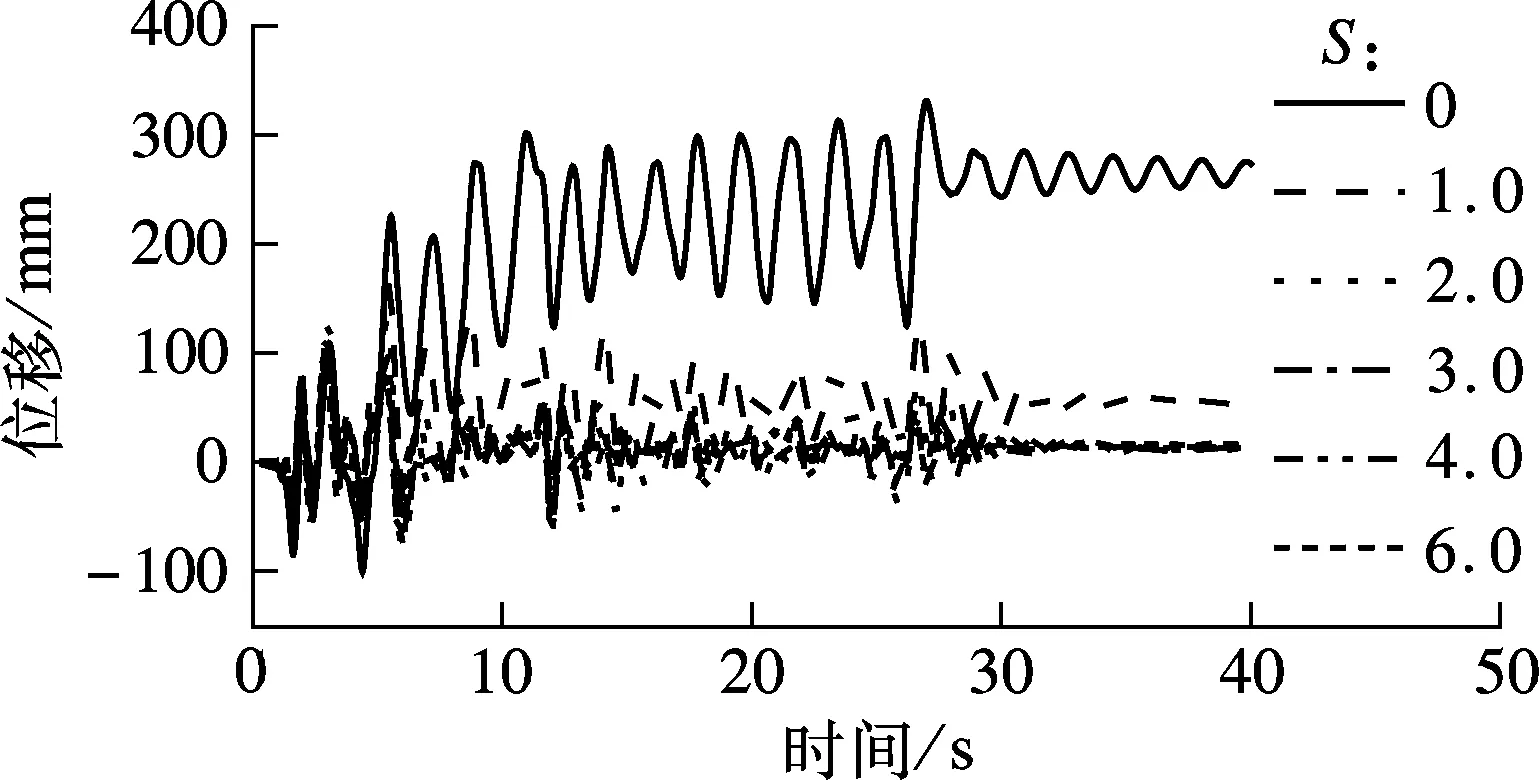
图5 工况1下结构的位移时程曲线

图6 工况1下位移和支撑-框架刚度比的关系曲线

3.2 支撑-框架屈服强度比

图4(b)为工况2下结构的侧向力F与顶点位移u的关系曲线．在工况2中,框架屈服强度保持不变,通过改变BRB屈服强度来改变D值,因此,D取值不同时对应结构的第一屈服点在同一斜线上,第二屈服点相同．图7(a)为工况2下位移与支撑-框架屈服强度比的关系曲线．由图可知,支撑-框架屈服强度比D的合理值为0.7．工况2下D对位移的影响不明显,但D不宜小于0.3,即BRB的屈服强度不宜小于100 MPa．

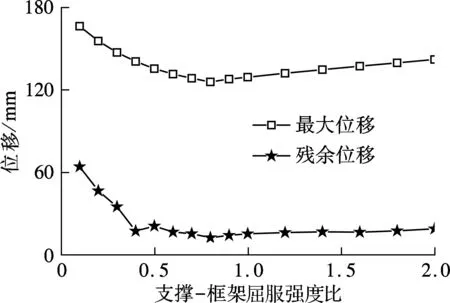
(a) 工况2

(b) 工况3

图4(c)为工况3下结构的侧向力F与顶点位移u关系曲线．在工况3下,BRB屈服强度保持不变,通过改变框架屈服强度来改变D值,因此,D取值不同时对应结构的第一屈服点相同,第二屈服点在同一斜线上．

图7(b)为工况3下位移与支撑-框架屈服强度比的关系曲线．由图可知,D的合理值为0.7．工况3下D对位移的影响不明显,但D不宜大于1,即框架梁柱的屈服强度不宜小于BRB的屈服强度(235 MPa)．目前,我国市场上BRB核心板多数采用Q235钢材,而框架通常使用Q235钢材或Q345钢材,说明BRB和梁柱用钢的屈服强度比值处于较为优化的范围内．

3.3 梁-柱线刚度比

图8为工况4下位移与梁-柱线刚度比的关系曲线．由图可知,梁-柱线刚度比ρ的合理值为0.45．当ρ<0.45时,其对位移的影响较大;当ρ≥0.45时,其对位移的影响较小．考虑工程实际,建议ρ取0.45～5.00．

图8 位移和梁-柱线刚度比的关系曲线

4 合理抗震参数结构算例

4.1 算例1

将S=2,D=0.7,ρ=0.45时的模型作为合理模型．图9为合理模型中顶点位移与基底剪力的关系曲线,该曲线与图2中的侧移分析曲线较为接近．

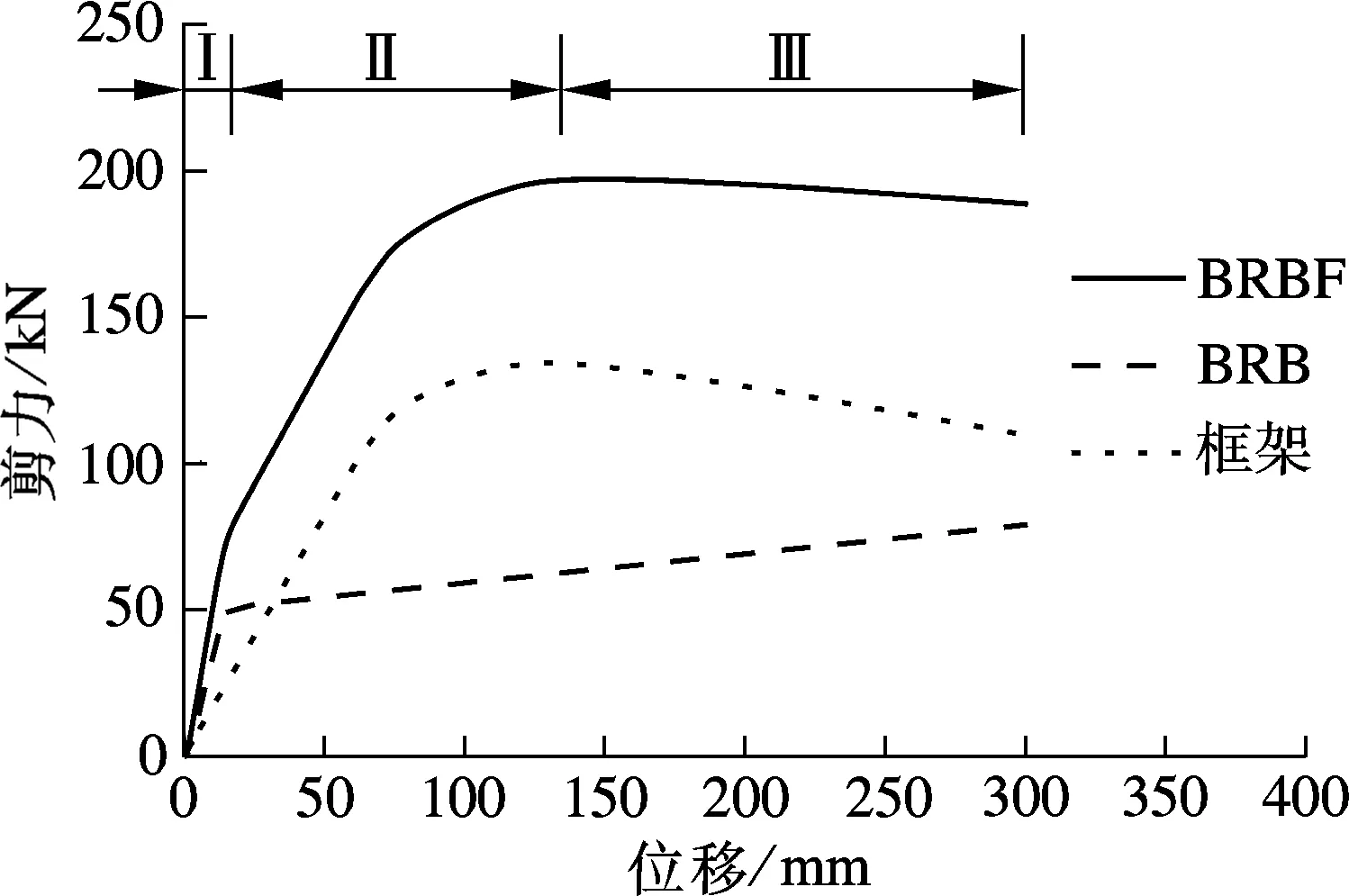
图9 合理模型的推覆曲线

框架或BRB承担的剪力与总剪力的比值称为剪力分担率．图10为剪力分担率随顶点位移的变化曲线．图中,区域Ⅰ为弹性阶段,由于BRB的侧向刚度为框架的2倍,则BRB承担的剪力比应为67%,但受到重力及其二阶效应的影响,BRB承担的剪力比并非常数;区域Ⅱ内BRB开始屈服,由于BRB的第二刚度较小,其剪力分担率随着位移的增加而减少,在区域Ⅱ和区域Ⅲ界限处达到最小,此时框架承担了较大部分的剪力;区域Ⅲ内BRB和框架共同屈服,假定BRB具有较好的延性,较大位移下BRB仍能保持第二刚度,BRB剪力分担率随着位移的增加而增大．

图10 剪力分担率-位移曲线

为了考察合理模型的屈服机制,在推覆过程中提取各个构件的内力(包括BRB轴力和梁柱端弯矩)．由图11可知,在单调推覆下的合理模型中,可以形成支撑-梁-柱屈服机制,表明单层BRBF抗震参数合理值是正确的．

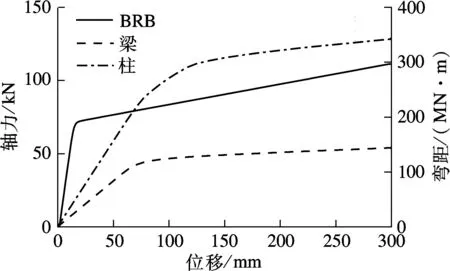
图11 构件内力-位移曲线

4.2 算例2

采用抗震参数合理值设计的3个单层五跨BRBF模型示意图见图12．这3个模型中的BRB分别采用中跨布置、边跨布置和满跨布置方式,标记为BRBF-1,BRBF-2和BRBF-3,其BRB面积之和相等,中跨布置支撑面积为1 350 mm2,其余参数同算例1．

对3个模型进行时程分析.由于采用了相同参数对进行设计,顶点位移反应几乎完全相同,BRBF-1,BRBF-2和BRBF-3的顶点位移最大值分别为120.7,120.9和123.4 mm,说明本文提出的3个参数可以表征单层BRBF整体动力特性．地震作用下BRB会引起相邻柱中产生附加轴力,支撑引起柱C1,C2和C3的附加轴力分别为373,196和90 kN,且支撑面积越大,附加轴力越大．这说明分散布置BRB有助于缓解BRB轴力竖向分力而导致的柱及其基础竖向内力的增加．

(a) BRBF-1

(b) BRBF-2

(c) BRBF-3

5 结论

1) 本文提出的抗震参数对结构的最大位移响应和残余位移都有较大影响．当S和ρ较小时,增大刚度比可以明显减小结构位移响应;D对结构的屈服位移和机制影响较大．抗震参数S,D,ρ的合理值分别为2,0.7和0.45～5.00．

2) 合理模型分析结果表明:在具有合理参数值的结构中,可以形成支撑-梁-柱的理想屈服机制;随着地震强度的增加,框架剪力分担率逐渐增大,此部分的剪力在设计中不容忽视．

3) BRB布置方式对结构顶点位移响应影响不大,对与其相邻的柱轴力则有较大影响,且BRB截面面积越大,影响越大．

4) 对于多高层BRBF而言,抗震参数沿楼层分布、高阶振型和框架柱引起的弯曲变形效应等问题需要在进一步研究．

References)

[1]Uang Chia-Ming, Nakashima Masayoshi, Tsai Keh-Chyuan. Research and application of buckling-restrained braced frames[J].InternationalJournalofSteelStructures, 2004, 4(4): 301-313.

[2]孙逊, 崔永平, 黄明, 等. 人民日报社报刊综合业务楼结构设计[J]. 建筑结构,2012, 42(9): 52-55. Sun Xun, Cui Yongping, Huang Ming, et al. Structural design of the People's Daily office building[J].BuildingStructure, 2012, 42(9): 52-55. (in Chinese)

[3]Jones P, Zareian F. Seismic response of a 40-storey buckling-restrained braced frame designed for the Los Angeles region[J].TheStructuralDesignofTallandSpecialBuildings, 2013, 22(3): 291-299.

[4]Ariyaratana C, Fahnestock L A. Evaluation of buckling-restrained braced frame seismic performance considering reserve strength[J].EngineeringStructures, 2011, 33(1): 77-89.

[5]贾明明, 张素梅. 采用抑制屈曲支撑的钢框架结构性能分析[J]. 东南大学学报:自然科学版, 2007, 37(6): 1041-1047. Jia Mingming, Zhang Sumei. Performance of steel frame installed with buckling-restrained braces[J].JournalofSoutheastUniversity:NaturalScienceEdition, 2007, 37(6): 1041-1047. (in Chinese)

[6]Ρalmer K D, Roeder C W, Lehman D E, et al. Experimental performance of steel braced frames subjected to bidirectional loading[J].JournalofStructuralEngineering, 2012, 139(8): 1274-1284.

[7]American Institute of Steel Construction. ANSI/AISC 341-10 Seismic provisions for structural steel buildings[S]. Chicago:American Institute of Steel Construction, 2010.

[8]上海市机电设计研究院有限公司,同济大学,中船第九设计研究院工程有限公司. DG/TJ08-32—2008 高层建筑钢结构设计规范[S]. 上海: 上海市建设和交通委员会, 2008.

[9]Kim J, Choi H. Behavior and design of structures with buckling-restrained braces[J].EngineeringStructures, 2004, 26(6): 693-706.

[10] 贾明明, 张素梅, 吕大刚, 等. 抑制屈曲支撑布置原则对钢框架抗震性能的影响[J]. 工程力学， 2009, 26(7):140-146. Jia Mingming, Zhang Sumei, Lü Dagang, et al. Influence of layout principle of buckling-restrained braces on aseismic performance of steel frame[J].EngineeringMechanics, 2009, 26(7): 140-146. (in Chinese)

[11] 赵瑛, 郭彦林. 防屈曲支撑框架设计方法研究[J]. 建筑结构， 2010, 40(1): 38-43, 85. Zhao Ying, Guo Yanlin. Research on design method of buckling restrained braced frames[J].BuildingStructure, 2010, 40(1): 38-43, 85. (in Chinese)

[12]中华人民共和国住房和城乡建设部. GB 50011—2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

Seismic parameters of single-layer buckling-restrained braced frame

Feng Yulong Wu Jing Meng Shaoping Fu Kang

(Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China)

To provide the design reference for the frame structure with buckling-restrained brace (BRB), the seismic parameters of the single-layer buckling-restrained braced frame (BRBF) structure are studied. By lateral displacement analysis, three key parameters characterizing the structural force and deformation, the BRB-to-frame stiffness ratio, the BRB-to-frame yield strength ratio and the beam-to-column line stiffness ratio, are derived. By taking the maximum displacement and the residual displacement under the specific ground motion as the evaluation indexes, parametric analyses are carried out. The analysis results show that when the BRB-to-frame stiffness ratio and the beam-to-column line stiffness ratio are small, both kinds of displacements decrease with the increase of the ratios. The BRB-to-frame yield strength ratio influences greatly on the structural yield displacement and mechanism. The reasonable values of the BRB-to-frame stiffness ratio, the BRB-to-frame yield strength ratio and the beam-to-column line stiffness ratio are 2, 0.7 and 0.45～5.00, respectively. Base on these reasonable values, two examples are designed and the corresponding seismic performance is analyzed. The results show that the BRB-beam-column yield mechanism is formed in the structures. After the BRB yields, the ratio of the shear forces of the frame increases gradually. The layout principle of BRB has almost no obvious influence on the roof displacement response, but affects significantly the axial force of the adjacent columns.

single-layer buckling-restrained braced frame; seismic parameters; reasonable parameter values; layout principle

10.3969/j.issn.1001-0505.2015.03.023

2014-12-30. 作者简介: 冯玉龙(1990—)，男，博士生；吴京(联系人)，男，博士，教授，博士生导师，seuwj@seu.edu.cn.

国家自然科学基金资助项目(51278105)、中央高校基本科研业务费专项资金资助项目、江苏省普通高校研究生科研创新计划资助项目(KYLX_0153).

冯玉龙,吴京,孟少平,等.单层屈曲约束支撑框架的抗震参数[J].东南大学学报:自然科学版,2015,45(3):544-549.

10.3969/j.issn.1001-0505.2015.03.023

TU352.1

A

1001-0505(2015)03-0544-06